Rewrite using a substitution Do not integrate 7

Re-write using a substitution. Do not integrate. ? ? ?

7. 1 Integration By Parts Start with the product rule: This is the Integration by Parts formula.

u differentiates to zero (usually). dv is easy to integrate. Or for a definite integral The Integration by Parts formula is a “product rule” for integration. Choose u in this order: LIPET Logs, Inverse trig, Polynomial, Exponential, Trig

When do you use Integration by Parts (IBP)? • Usually, the function is the product of 2 different types of functions. Polynomial, log, exponential, trig, etc. • U-substitution does not produce a known pattern to integrate. 2 different types of functions, but… 2 different types of functions, and no u-sub works.

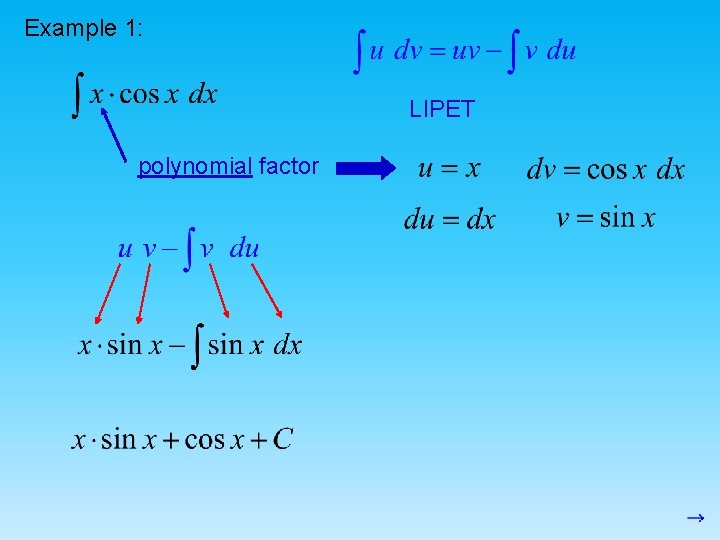
Example 1: LIPET polynomial factor

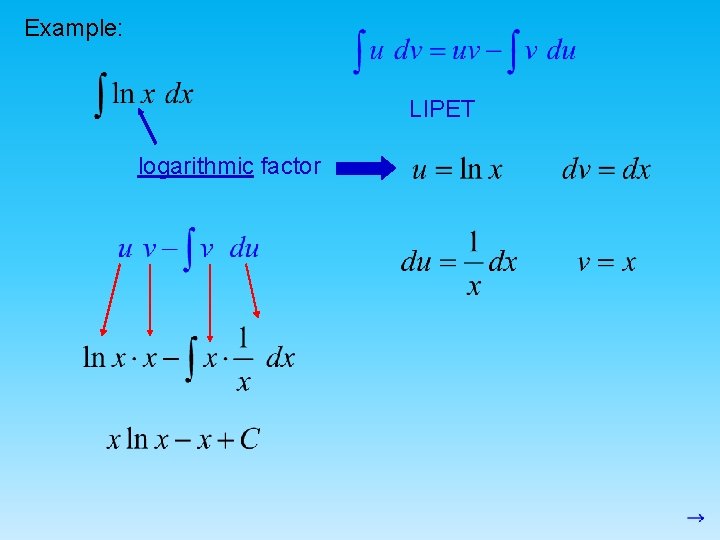
Example: LIPET logarithmic factor

Example 4: LIPET This is still a product, so we need to use integration by parts again.

Example 5: LIPET This is the expression we started with!

Example 6: LIPET

Example 6: This is called “solving for the unknown integral. ” It works when both factors integrate and differentiate forever.

A Shortcut: Tabular Integration Tabular integration works for integrals of the form: where: Differentiates to zero in several steps. Integrates repeatedly.

Compare this with the same problem done the other way:

Example 5: LIPET This is easier and quicker to do with tabular integration!

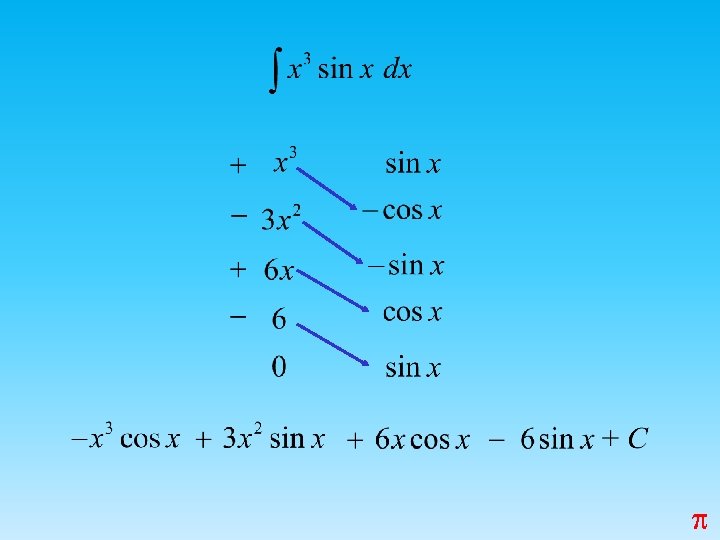
p

Doesn’t follow any pattern for integration that we know.

What if… So instead: Then…

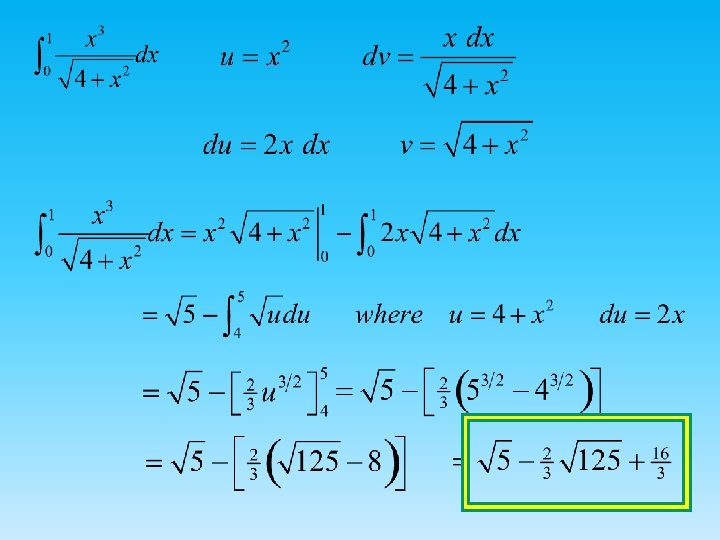
Homework: Page 492 5, 11, 19, 27, 31, 35, 39, 57, 61, 64 b