Reviso Matemtica Profa Mercedes Gonzales Mrquez Sistema de

Revisão Matemática Profa. Mercedes Gonzales Márquez

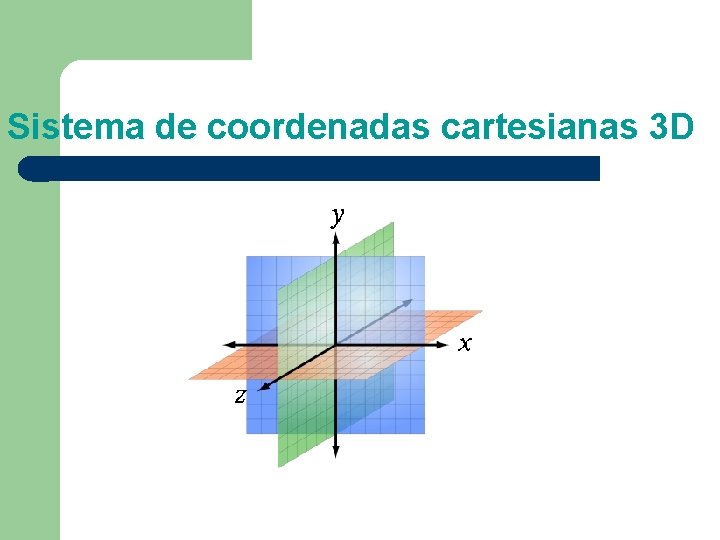
Sistema de coordenadas cartesianas 3 D

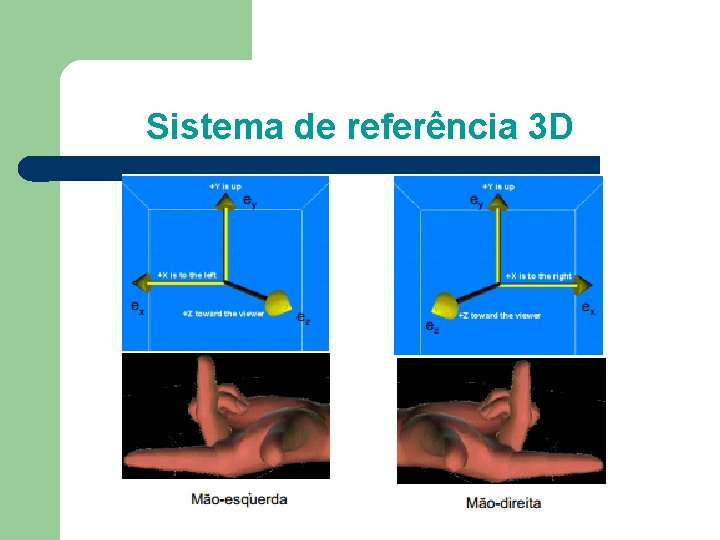
Sistema de referência 3 D

Equação da Reta

Equação da Circunferência

Vetores Um vetor v é uma entidade geométrica com magnitude (comprimento) e direção, representado graficamente por um segmento de linha orientado. Aplicações em CG ? – representação de direção (onde está o personagem, onde está o observador, onde está a luz, ou direção perpendicular a um

Vetores Módulo de um vetor v consiste numa função que associa cada vetor de um espaço vetorial em um número real não negativo. O conceito de módulo é estreitamente ligado ao de comprimento do vetor. Distância Euclideana ||v || = d = sqrt (x 2 + y 2)

Vetores Produto Escalar Referenciado por v. w Usa Norma Euclideana (módulo) Definido como: v. w = ||v|| ||w|| cos θ = vxwx + vywy + vzwz Se o ângulo entre v e w é de 90 o (vetores perpendiculares) v. w = 0

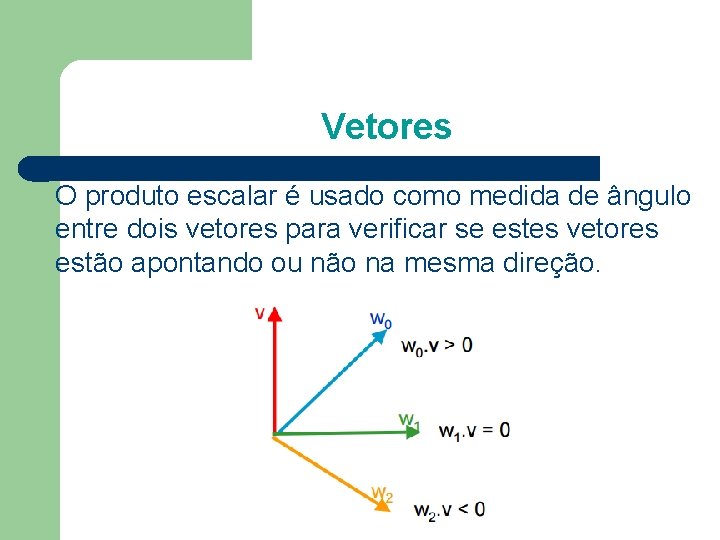
Vetores O produto escalar é usado como medida de ângulo entre dois vetores para verificar se estes vetores estão apontando ou não na mesma direção.

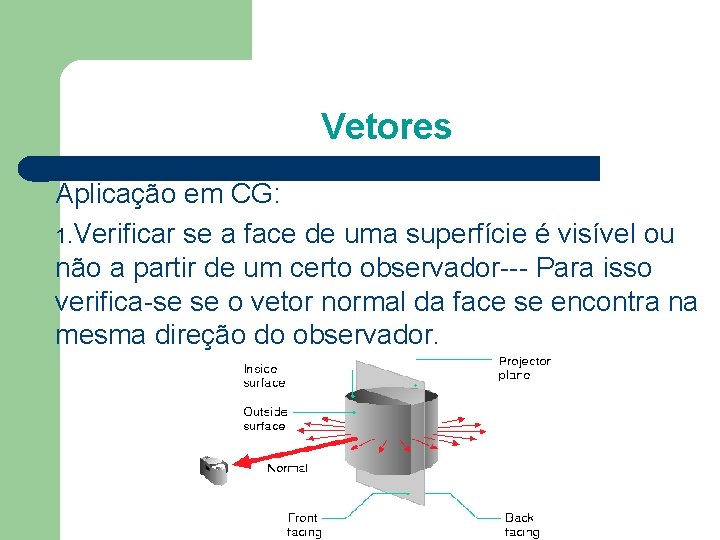
Vetores Aplicação em CG: 1. Verificar se a face de uma superfície é visível ou não a partir de um certo observador--- Para isso verifica-se se o vetor normal da face se encontra na mesma direção do observador.

Vetores 2. Verificar se a face de uma superfície é visível ou não a partir de um observador --- Para isso verificase se o vetor normal da face se encontra na mesma direção da fonte de luz.

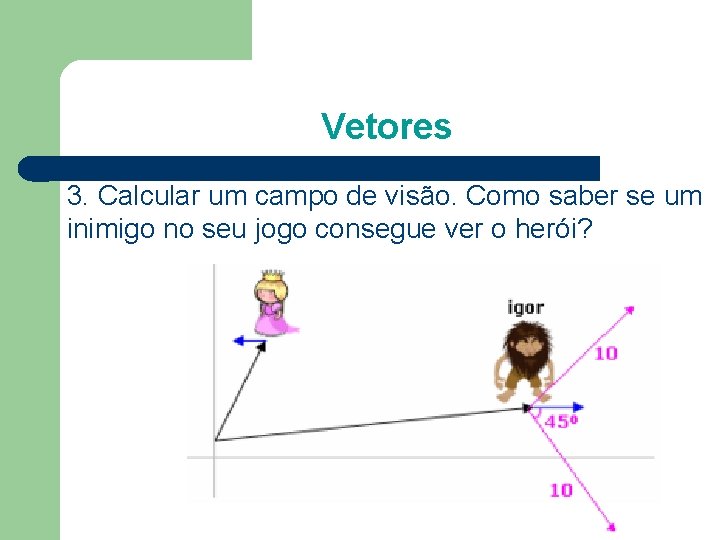
Vetores 3. Calcular um campo de visão. Como saber se um inimigo no seu jogo consegue ver o herói?

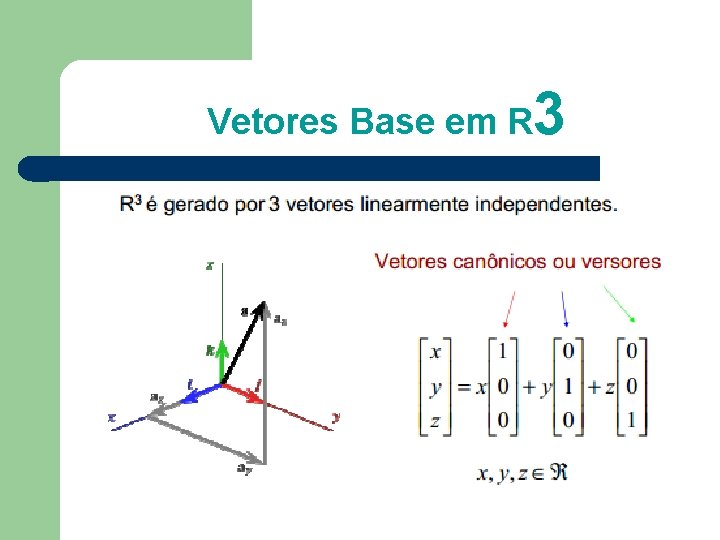
Vetores Base em R 3

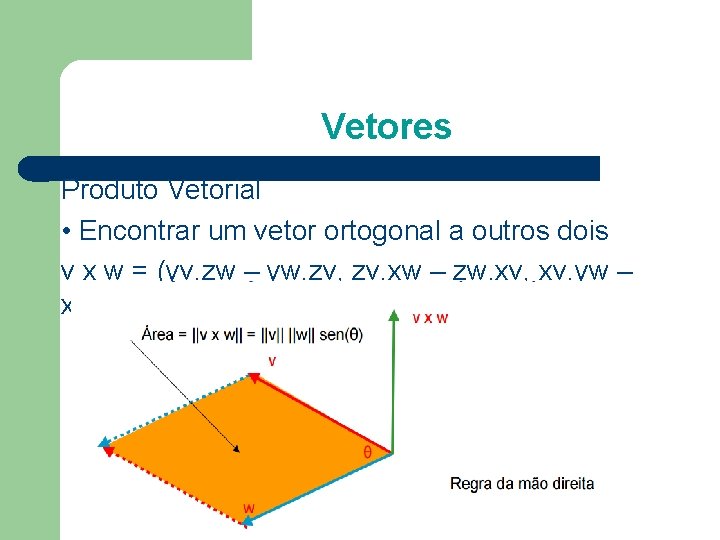
Vetores Produto Vetorial • Encontrar um vetor ortogonal a outros dois. a × b = [a 2 b 3 − a 3 b 2, a 3 b 1 − a 1 b 3, a 1 b 2 − a 2 b 1]. A notação acima também pode ser escrita formalmente como o determinante de uma matriz

Vetores Produto Vetorial • Encontrar um vetor ortogonal a outros dois v x w = (yv. zw – yw. zv, zv. xw – zw. xv, xv. yw – xw. yv)

Vetores Como se encontra o vetor normal de um plano?

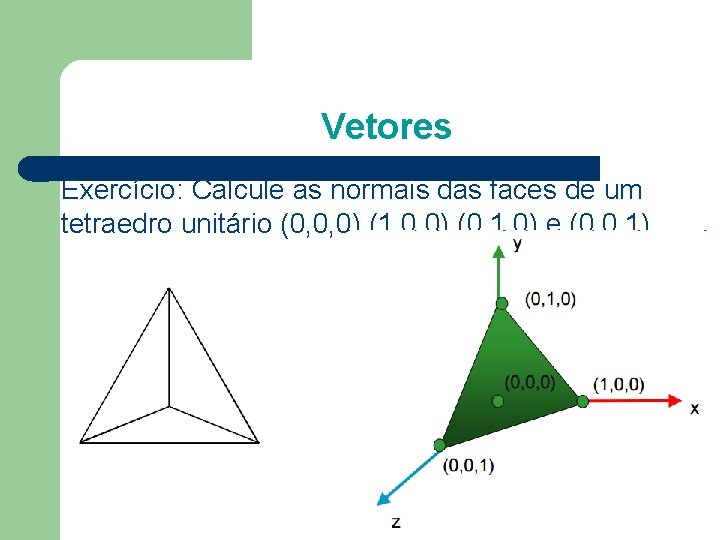
Vetores Exercício: Calcule as normais das faces de um tetraedro unitário (0, 0, 0) (1, 0, 0) (0, 1, 0) e (0, 0, 1)

Revisão de matrizes e vetores Matrizes em Computação Gráfica – As matrizes são mais fáceis de usar e entender do que as equações algébricas – As matrizes são parecidas com o modelo organizacional da memória dos computadores – Matrizes quadradas de 2 x 2 – 2 D (x, y) 3 x 3 – 3 D (x, y, z)

Aritmética de Vetores e Matrizes Adição : [1 2 3] + [2 0 1] = [3 2 4] Subtração : [1 2 3] – [2 0 1] = [-1 2 2] Multiplicação de uma matriz por um escalar: Multiplicação entre matrizes:

Aritmética de Vetores e Matrizes Multiplicação entre matrizes(exemplos) Possível Impossível Possível Transposta de um vetor ou matriz:

Propriedades do Produto de Matrizes Associativa: A. (B. D) = (A. B). D. Distributiva à direita: A. (B + D) = A. B + A. D. Distributiva à esquerda: (A + B). D = A. D + B. D. Existência de elemento neutro: A. I = I. A = A. Uma matriz I de ordem n é uma matriz identidade, se ijk = 1, quando j = k e os outros elementos são nulos.