Revisiting the LeastSquares Procedure for Gradient Reconstruction on

Revisiting the Least-Squares Procedure for Gradient Reconstruction on Unstructured Meshes Dimitri J. Mavriplis National Institute of Aerospace Hampton, VA 23666

Motivation • Originated from study of matrix dissipation versus upwind schemes for unstructured mesh RANS solver • Least Squares Gradient now standard technique for higher order accuracy with upwind schemes • Unexpected behavior observed (with entropy fix) 1 week project 3 month investigation

Summary of Findings • Least squares gradient construction may under-predict gradients by orders of magnitude (~100% error) – Vertex, cell centered, simplicial, mixed elements • Subtle mechanism – Apparently has gone unnoticed in literature – May not show up in standard test cases • Similar results: N. B. Petrovskaya: ``The impact of grid cell geometry on the least squares gradient reconstruction’’, Keldysh Institute of Applied Math. , Russian Academy of Sciences, April 2003

Spatial Discretization • Mixed Element Meshes – Tetrahedra, Prisms, Pyramids, Hexahedra • Control Volume Based on Median Duals – Fluxes based on edges Fik = F(u. L) + F(u. R) + T |L| T-1 (u. L –u. R) - Upwind discretization - Matrix artificial dissipation – Single edge-based data-structure represents all element types

Upwind Discretization • First order scheme • Second order scheme • Gradients evaluated at vertices by Least-Squares • Limit Gradients for Strong Shock Capturing

Matrix Artificial Dissipation • First order scheme • Second order scheme • By analogy with upwind scheme: • Blending of 1 st and 2 nd order schemes for strong shock capturing

Entropy Fix L matrix: diagonal with eigenvalues: u, u, u, u+c, u-c • Robustness issues related to vanishing eigenvalues • Limit smallest eigenvalues as fraction of largest eigenvalue: |u| + c – u = sign(u) * max(|u|, d(|u|+c)) – u+c = sign(u+c) * max(|u+c|, d(|u|+c)) – u – c = sign(u -c) * max(|u-c|, d(|u|+c))

Entropy Fix – u = sign(u) * max(|u|, d(|u|+c)) – u+c = sign(u+c) * max(|u+c|, d(|u|+c)) – u – c = sign(u -c) * max(|u-c|, d(|u|+c)) d = 0. 1 : typical value for enhanced robustness d = 1. 0 : Scalar dissipation - L becomes scaled identity matrix – T |L| T-1 becomes scalar quantity – Simplified (lower cost) dissipation operator • Applicable to upwind art. dissipation schemes

Green-Gauss Gradient Construction – Contour integral around control volume – Generally NOT Exact for linear functions • Only for vertex discretizations on triangles/tetrahedra – Accuracy dependant on cell shapes – Poor solver robustness reported for RANS cases

Least Squares Gradient Construction – Formally unrelated to grid topology – Natural to base point sample on grid stencil – Exact for linear functions on all grid/discretization types – More accurate gradients on distorted meshes – Reported to be more robust for viscous flows

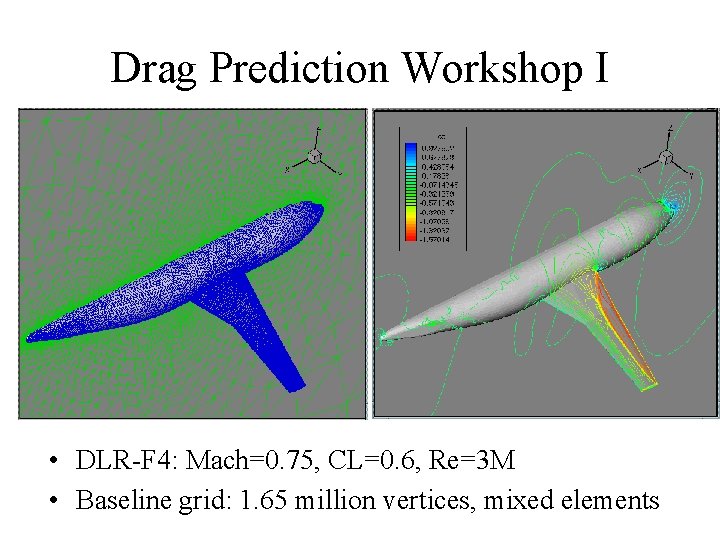
Drag Prediction Workshop I • DLR-F 4: Mach=0. 75, CL=0. 6, Re=3 M • Baseline grid: 1. 65 million vertices, mixed elements

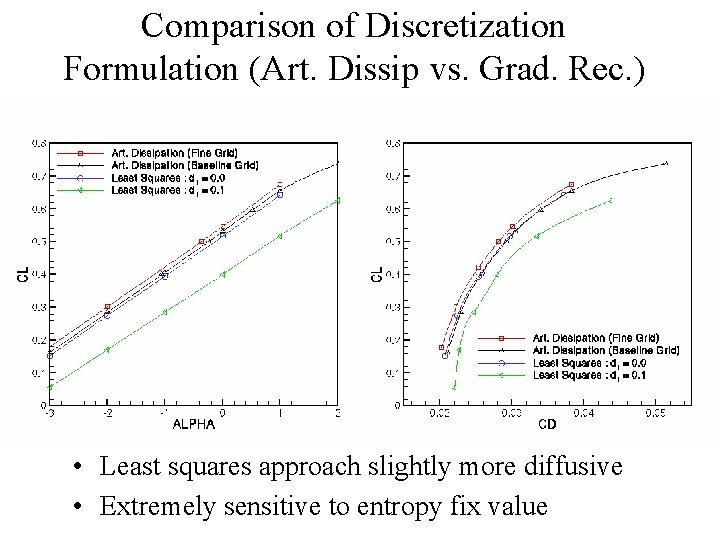
Comparison of Discretization Formulation (Art. Dissip vs. Grad. Rec. ) • Least squares approach slightly more diffusive • Extremely sensitive to entropy fix value

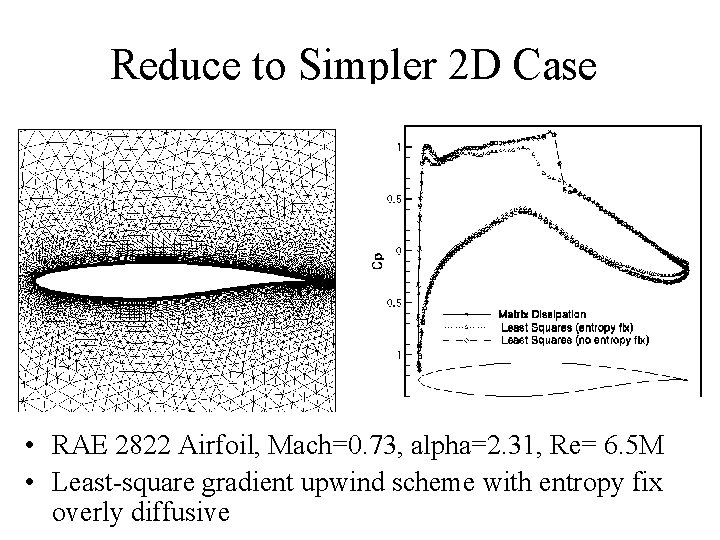
Reduce to Simpler 2 D Case • RAE 2822 Airfoil, Mach=0. 73, alpha=2. 31, Re= 6. 5 M • Least-square gradient upwind scheme with entropy fix overly diffusive

Gradient Accuracy Study • Least-Squares, Green-Gauss, Finite Difference • Discretization type (cell-vertex), element type • Exact analytic function (non-linear) – Compute exact error – Function similar to flow gradients – Boundary layer regions

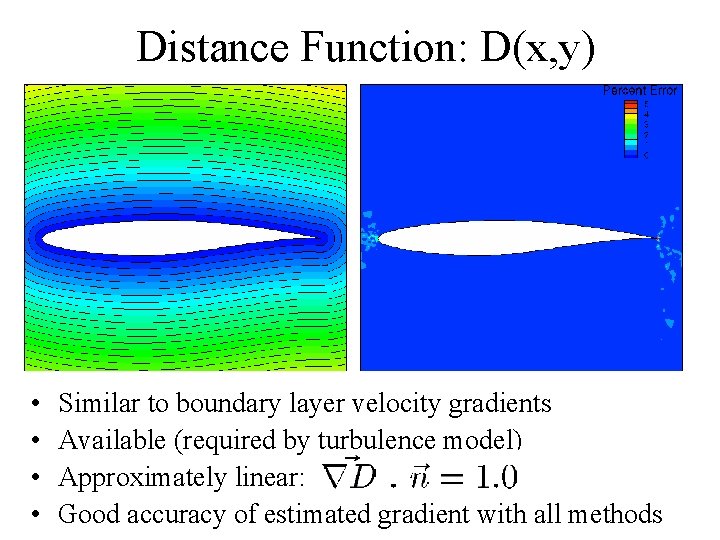
Distance Function: D(x, y) • • Similar to boundary layer velocity gradients Available (required by turbulence model) Approximately linear: Good accuracy of estimated gradient with all methods

Non-Linear Function • Non-linear function required for adequate test – a = 200 (reduces roundoff error for small D) • Exact Gradient : Since

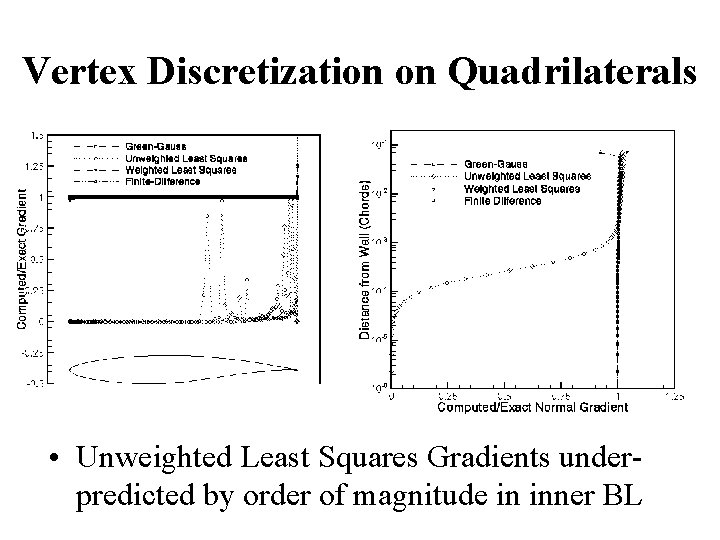
Gradient Error Study • Compare calculated and exact Gradient of function F at vertices of mixed element unstructured mesh (quadrilateral elements near airfoil surfaces)

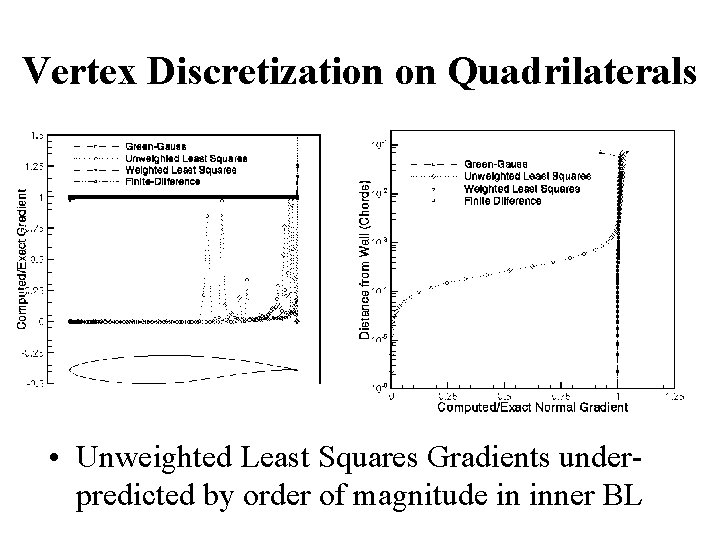
Vertex Discretization on Quadrilaterals • Unweighted Least Squares Gradients underpredicted by order of magnitude in inner BL

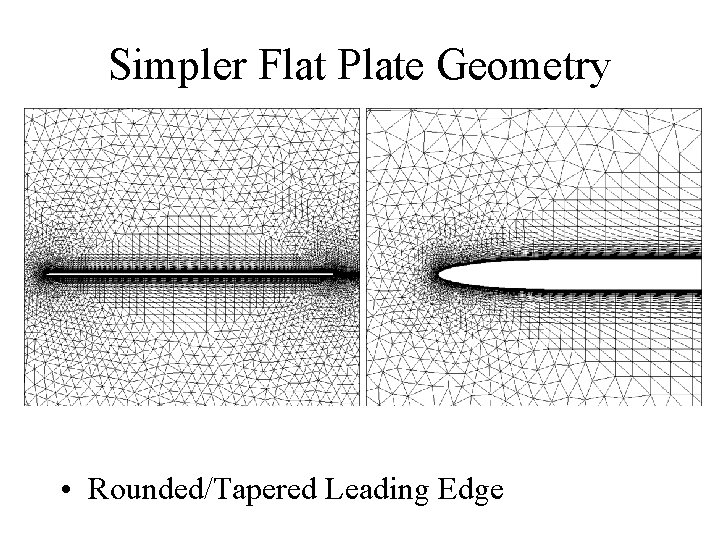
Simpler Flat Plate Geometry • Rounded/Tapered Leading Edge

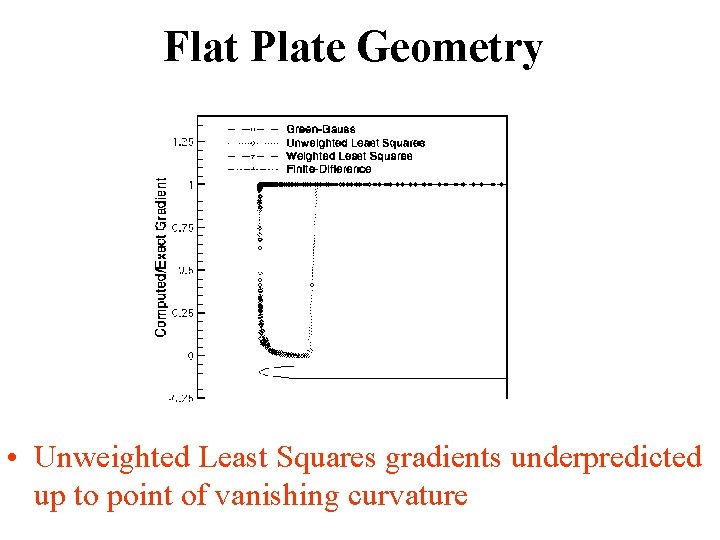
Flat Plate Geometry • Unweighted Least Squares gradients underpredicted up to point of vanishing curvature

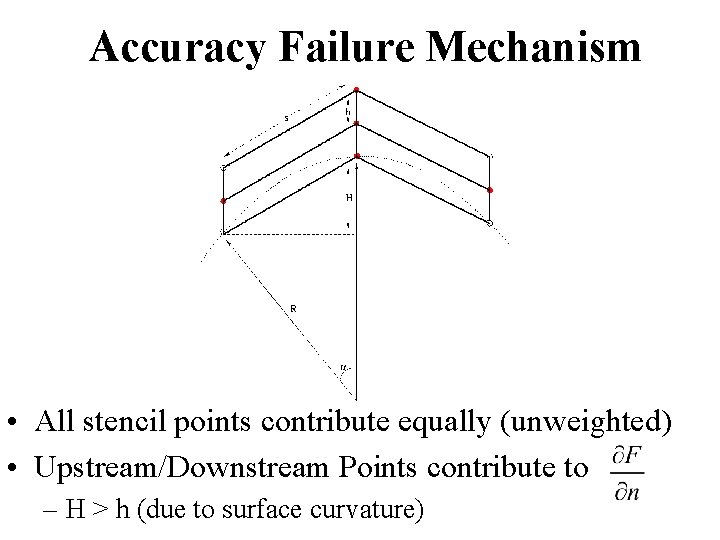
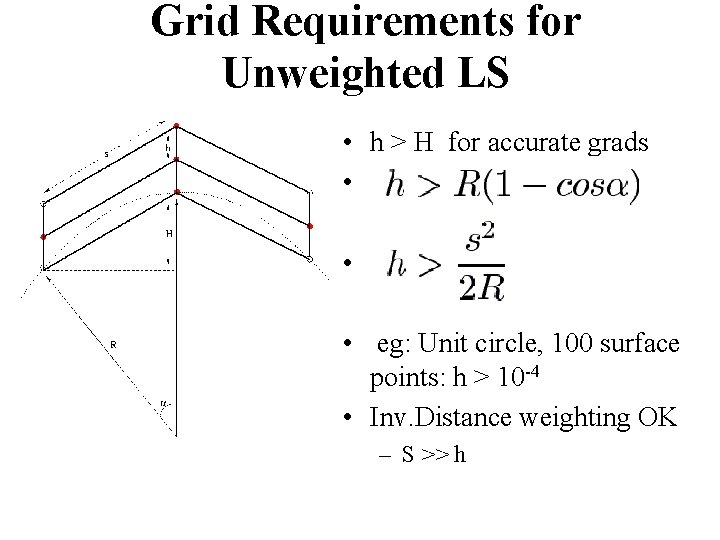
Accuracy Failure Mechanism • All stencil points contribute equally (unweighted) • Upstream/Downstream Points contribute to – H > h (due to surface curvature)

Grid Requirements for Unweighted LS • h > H for accurate grads • • • eg: Unit circle, 100 surface points: h > 10 -4 • Inv. Distance weighting OK – S >> h

Vertex Discretization on Quadrilaterals • Unweighted Least Squares Gradients underpredicted by order of magnitude in inner BL

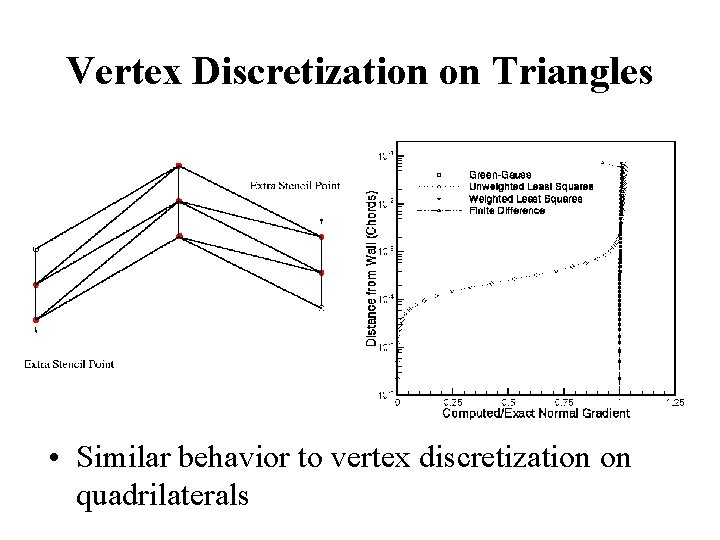
Vertex Discretization on Triangles • Similar behavior to vertex discretization on quadrilaterals

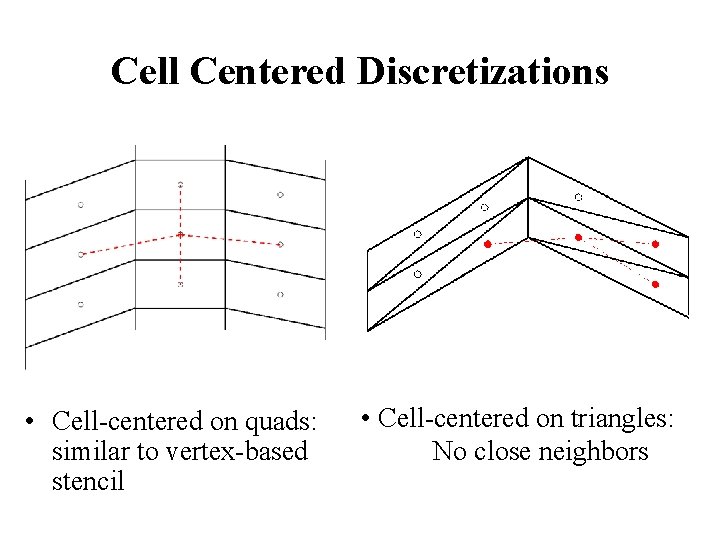
Cell Centered Discretizations • Cell-centered on quads: similar to vertex-based stencil • Cell-centered on triangles: No close neighbors

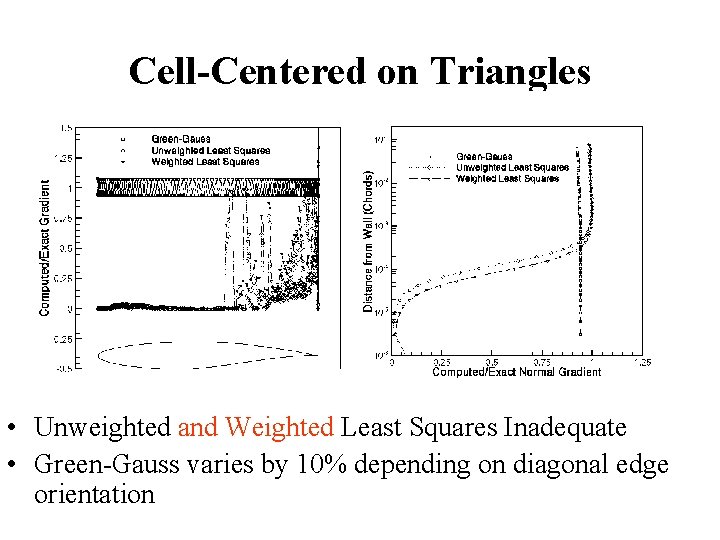
Cell-Centered on Triangles • Unweighted and Weighted Least Squares Inadequate • Green-Gauss varies by 10% depending on diagonal edge orientation

Effect on Solution Accuracy • How can good solution accuracy be obtained in the presence of poor gradient estimates ? • Why is accuracy so sensitive to small values of entropy fix ? • Flow alignment phenomena • Occurs in exact same regions as inaccurate gradients • Inner BL region

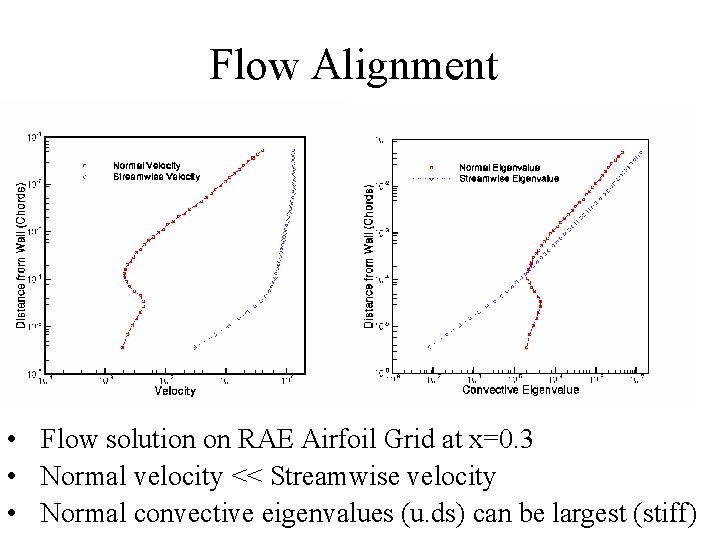
Flow Alignment • Flow solution on RAE Airfoil Grid at x=0. 3 • Normal velocity << Streamwise velocity • Normal convective eigenvalues (u. ds) can be largest (stiff)

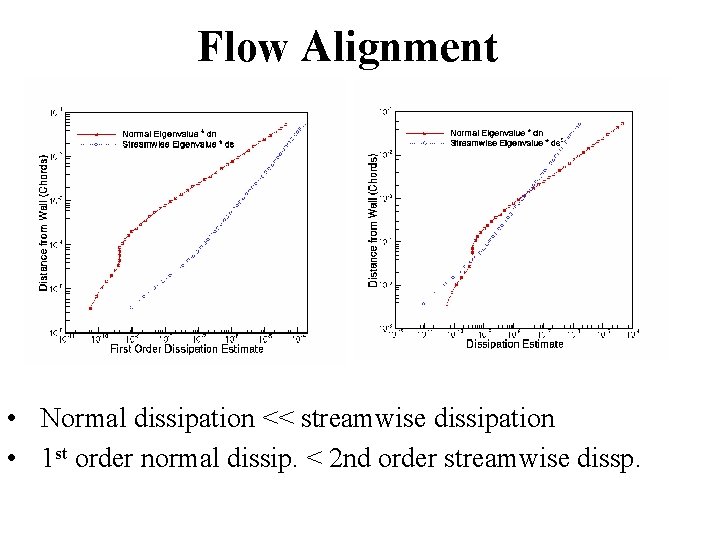
Flow Alignment • Normal dissipation << streamwise dissipation • 1 st order normal dissip. < 2 nd order streamwise dissp.

Flow Alignment • Entropy fix: ufix = sign(u). min (|u|, d(|u|+c)) • For aligned flow – Large increase in ufix for small values of d – Explains solution sensitivity to entropy fix • Flow alignment irrelevant for acoustic modes – Good overall accuracy retained in spite of poor resolution of acoustic modes in BL (? )

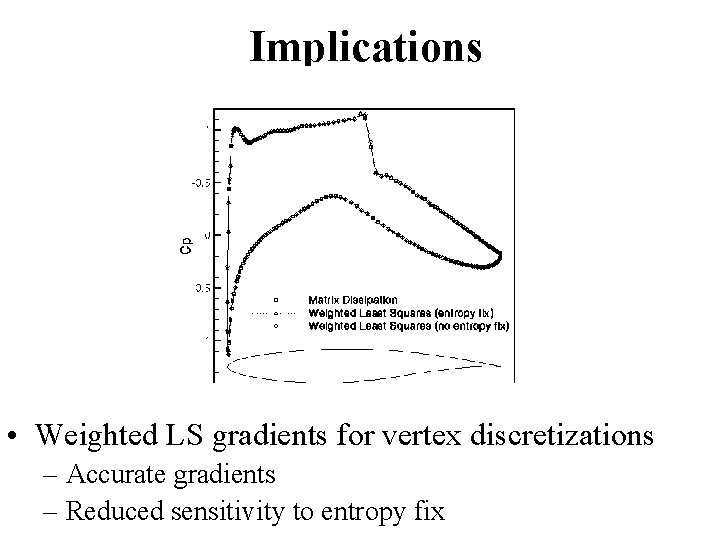
Implications • Weighted LS gradients for vertex discretizations – Accurate gradients – Reduced sensitivity to entropy fix

Implications • Unweighted LS more accurate on isotropic grids • Unweighted LS inaccurate on stretched meshes – Effect mitigated by flow alignment • Inaccurate grads only in presence of curvature – Problem not seen for flat plate BL test case

Implications • Weighted LS or Green-Gauss gradients more accurate overall – Robustness issues reported • Unweighted LS Grads more robust – Not because of superior gradient estimates – Because solution is 1 st order (limited) in BL • Viscous (NS) terms based on LS grads could pass flat plate test, but be disastrous

Conclusions • Unweighted LS grads acceptable – Must be used only for reconstruction in convective terms – No entropy fix • Weighted LS grads offer superior accuracy – Result in well conditioned system of equations for gradient calculation • Stencils require close normal neighbor points – Semi-structured BL meshes • Robustness issues remain (further investigation) • Alternate construction techniques (further investigation) – Dimensional splitting – Gradient projection (Desideri), SLIP (Jameson) – Other approaches (Frink, Rausch, Batina and Yang) etc.