REVISION Topic 1 and Data analysis Statistics Topic

REVISION : Topic 1 and Data analysis Statistics

Topic 1 –guide • • • STATE that error bars are a graphical representation of the variability of data. CALCULATE the mean and standard deviation of a set of values. STATE that the term standard deviation is used to summarize the spread of values around the mean, and that 68% of the values fall within one standard deviation of the mean. ---------------------------------------------------------------- • EXPLAIN how the standard deviation is useful for comparing the means and the spread of data between two or more samples. • DEDUCE the significance of the difference between two sets of data using calculated values for t and the appropriate tables. • EXPLAIN that the existence of a correlation does not establish that there is a causal relationship between two variables.

Topic 1 –guide • Mean • Standard deviation • t-tests and significant differences • Correlation

Topic 1 –guide • Mean • Standard deviation • t-tests and significant differences • Correlation

Calculating a mean •

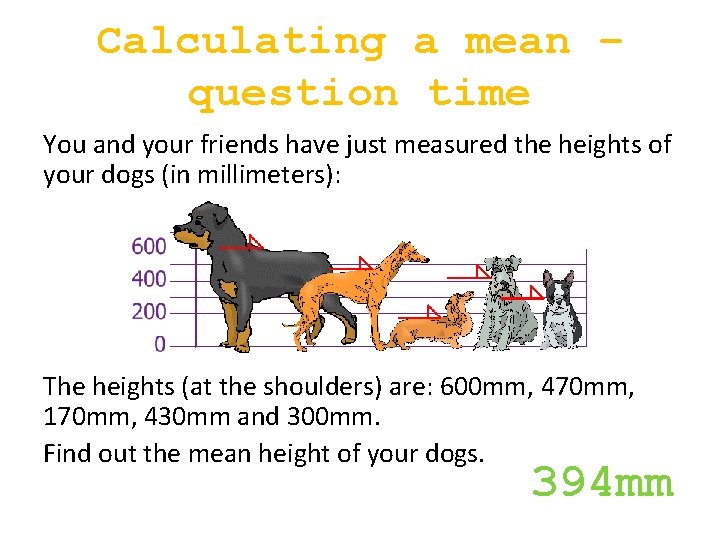
Calculating a mean – question time You and your friends have just measured the heights of your dogs (in millimeters): The heights (at the shoulders) are: 600 mm, 470 mm, 170 mm, 430 mm and 300 mm. Find out the mean height of your dogs. 394 mm

Topic 1 –guide • Mean • Standard deviation • t tests and significant differences • Correlation

Calculating the standard deviation •

Calculating the standard deviation – question time You and your friends have just measured the heights of your dogs (in millimeters): The heights (at the shoulders) are: 600 mm, 470 mm, 170 mm, 430 mm and 300 mm. Find out the standard deviation in the height of your dogs. 147 mm

Calculating the standard deviation DID YOU KNOW that your little scientific calculators also calculate the mean and standard deviation for you? ?

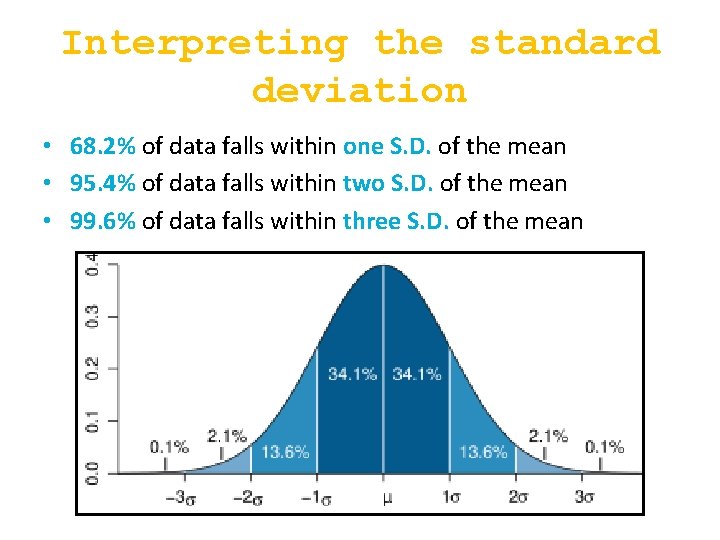
Interpreting the standard deviation STATE that the term standard deviation is used to summarize the spread of values around the mean, and that 68% of the values fall within one standard deviation of the mean.

Interpreting the standard deviation • 68. 2% of data falls within one S. D. of the mean • 95. 4% of data falls within two S. D. of the mean • 99. 6% of data falls within three S. D. of the mean

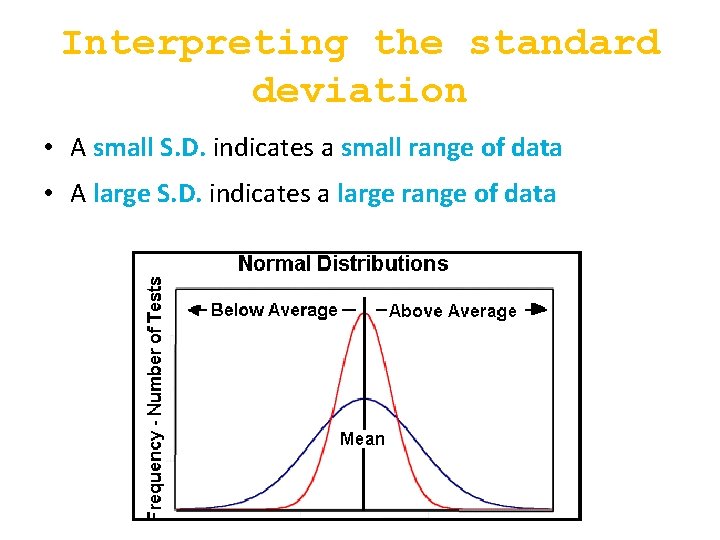
Interpreting the standard deviation • A small S. D. indicates a small range of data • A large S. D. indicates a large range of data

Interpreting the standard deviation • S. D. used to compare means and variability of data between two or more samples • If the S. D. is greater than the difference between two means, then the difference is not statistically significant – this will lead to overlapping error bars on a graph • Remember: small samples are unreliable!!!!!!!

Using the standard deviation STATE error bars are a graphical representation of the variability of data.

Mean & standard deviation – question time The lengths of a sample of tiger canines were measured. 68% of the lengths fell within a range between 15 mm and 45 mm. The mean was 30 mm. What is the standard deviation of this sample? 15 mm

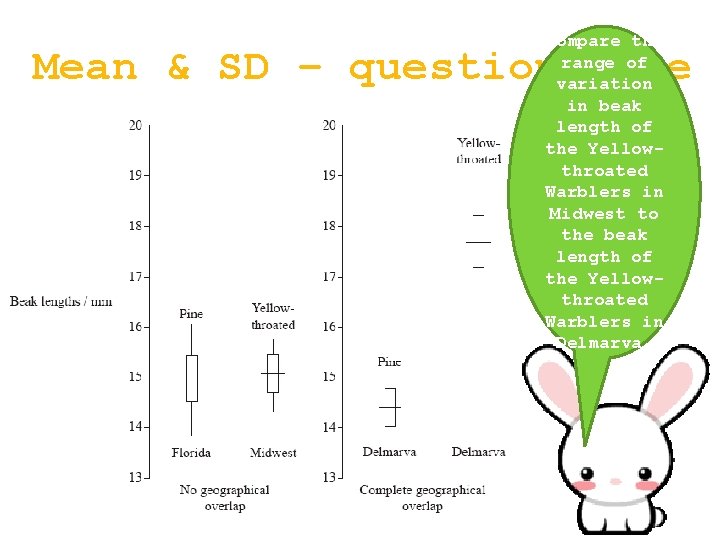
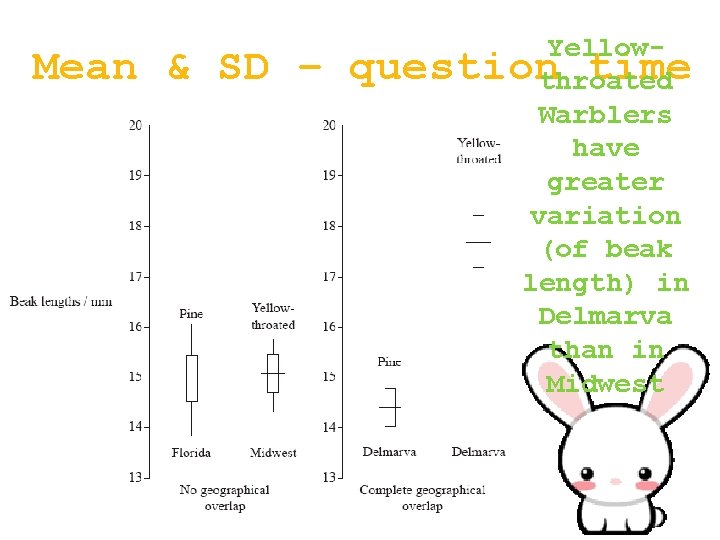
Compare the range of variation in beak length of the Yellowthroated Warblers in Midwest to the beak length of the Yellowthroated Warblers in Delmarva. Mean & SD – question time

Mean & SD – Yellowquestion time throated Warblers have greater variation (of beak length) in Delmarva than in Midwest

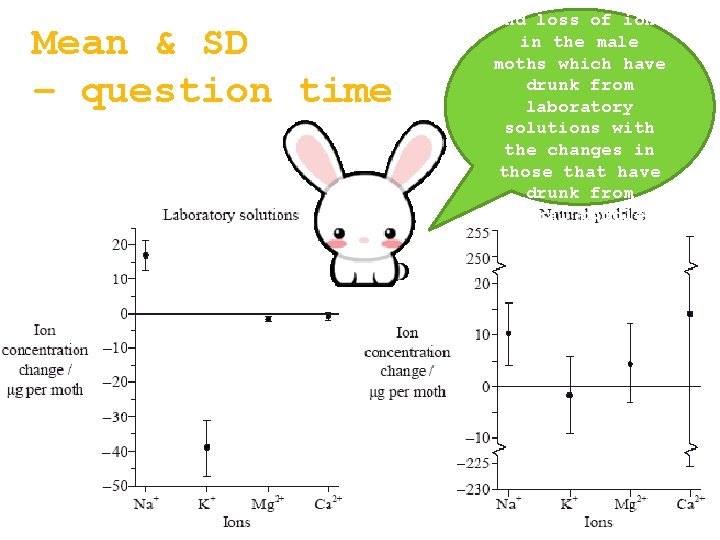
Mean & SD – question time Compare the gain and loss of ions in the male moths which have drunk from laboratory solutions with the changes in those that have drunk from natural puddles.

Mean & SD – question time Sodium was retained from lab solutions and natural puddles; Potassium was lost from lab solutions but uncertain loss/gain from natural puddles; Slight loss of magnesium from lab solutions and uncertain gain/loss from natural puddles; Variation in data for calcium; More conclusive results in lab solutions / conditions more reliable in lab / greater variation in natural puddles;

Topic 1 –guide • Mean • Standard deviation • t-tests and significant differences • Correlation

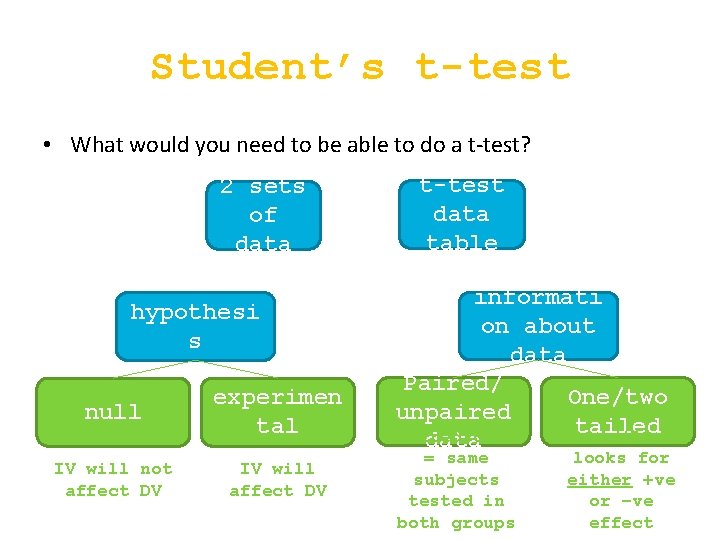
Student’s t-test • What is a t-test? a statistical test used to determine the significance of the difference between two means. • Why would we need to calculate it? If we want to confirm an experimental hypothesis and determine with confidence that the IV has contributed significantly to the change in the DV.

Student’s t-test • What would you need to be able to do a t-test? 2 sets of data hypothesi s null experimen tal IV will not affect DV IV will affect DV t-test data table informati on about data Paired/ One/two unpaired tailed Paired Two tailed = data = same subjects tested in both groups looks for either +ve or –ve effect

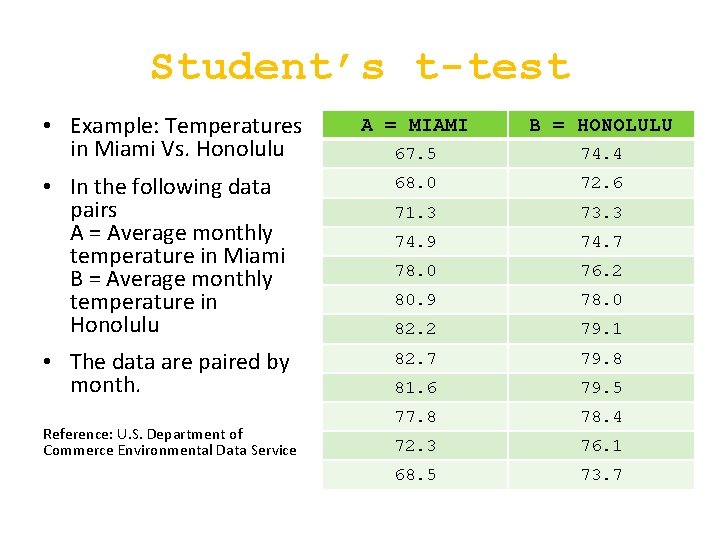
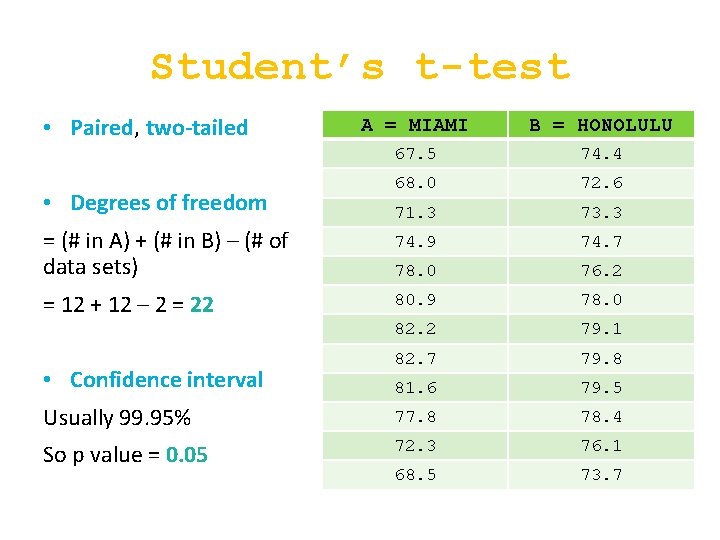
Student’s t-test • Example: Temperatures in Miami Vs. Honolulu • In the following data pairs A = Average monthly temperature in Miami B = Average monthly temperature in Honolulu • The data are paired by month. Reference: U. S. Department of Commerce Environmental Data Service A = MIAMI B = HONOLULU 67. 5 74. 4 68. 0 72. 6 71. 3 73. 3 74. 9 74. 7 78. 0 76. 2 80. 9 78. 0 82. 2 79. 1 82. 7 79. 8 81. 6 79. 5 77. 8 78. 4 72. 3 76. 1 68. 5 73. 7

Student’s t-test • Paired, two-tailed A = MIAMI B = HONOLULU 67. 5 74. 4 68. 0 72. 6 71. 3 73. 3 = (# in A) + (# in B) – (# of data sets) 74. 9 74. 7 78. 0 76. 2 = 12 + 12 – 2 = 22 80. 9 78. 0 82. 2 79. 1 82. 7 79. 8 81. 6 79. 5 Usually 99. 95% 77. 8 78. 4 So p value = 0. 05 72. 3 76. 1 68. 5 73. 7 • Degrees of freedom • Confidence interval

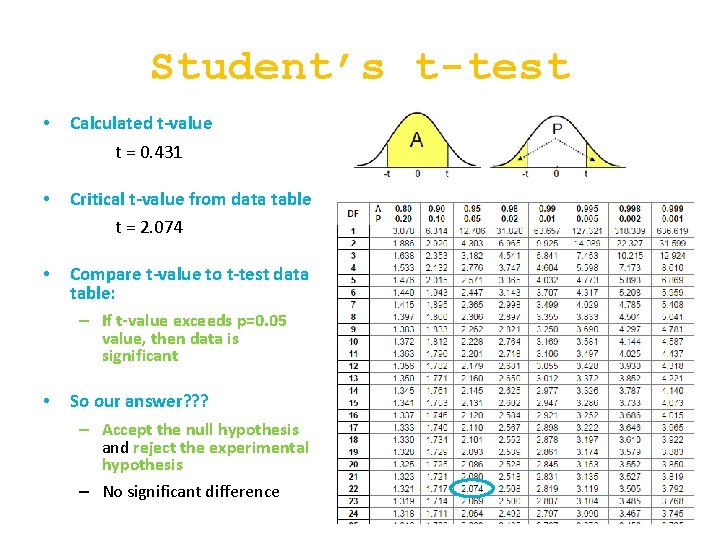
Student’s t-test • Calculated t-value t = 0. 431 • Critical t-value from data table t = 2. 074 • Compare t-value to t-test data table: – If t-value exceeds p=0. 05 value, then data is significant • So our answer? ? ? – Accept the null hypothesis and reject the experimental hypothesis – No significant difference

t-test – question time The Which hypothesis can be tested using the t-test? A. The difference in variation between two samples is not significant. B. The difference between observed values and expected values is not significant. C. The change in one variable is not correlated with a change in another variable. D. The difference between the means in two samples is not significant.

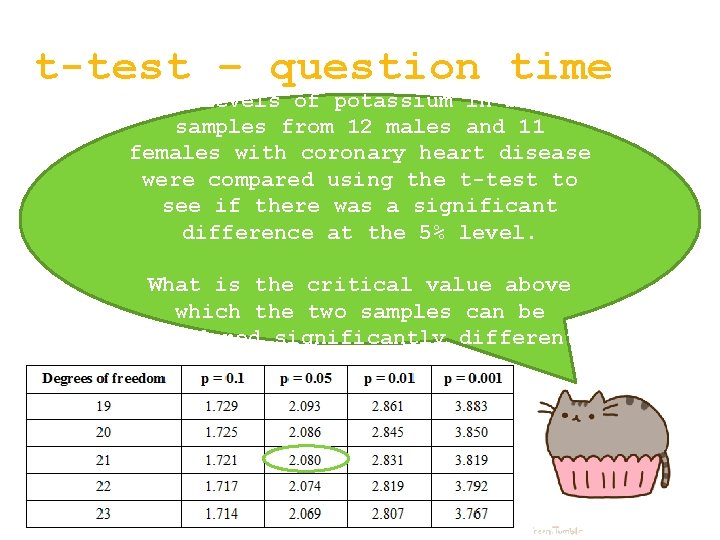
t-test – question time The levels of potassium in blood samples from 12 males and 11 females with coronary heart disease were compared using the t-test to see if there was a significant difference at the 5% level. What is the critical value above which the two samples can be considered significantly different?

Topic 1 –guide • Mean • Standard deviation • t-tests and significant differences • Correlation

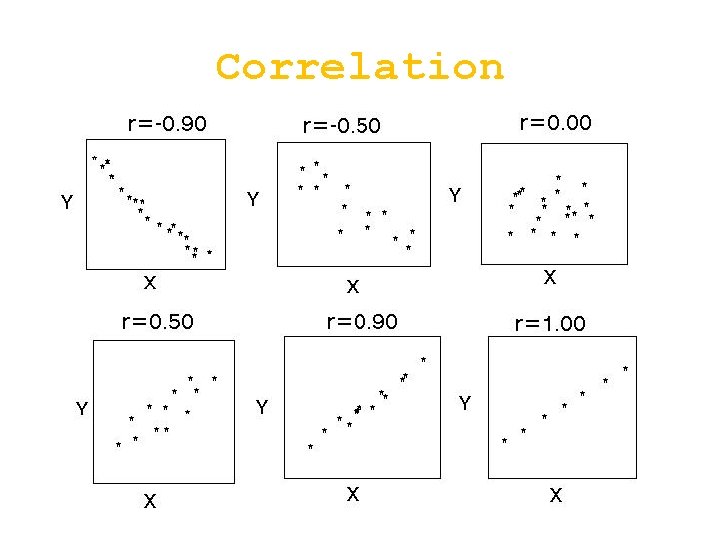
Correlation • Correlation is not causation! • Correlation means that there is a relationship between two (or more) things. • This DOES NOT MEAN that one has caused the other to occur. • Correlation describes the strength and direction of a linear relationship between two variables • Use the Pearson correlation coefficient (r), ranging from -1 to +1.

Correlation

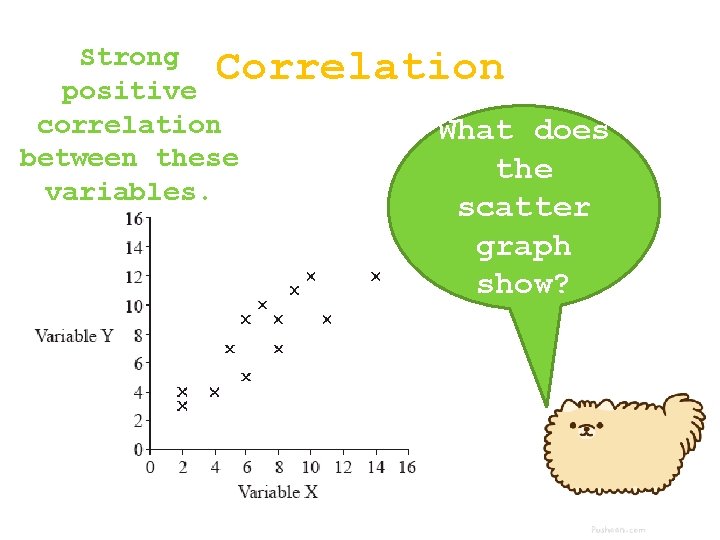
Strong Correlation positive correlation What does between these the variables. scatter graph show?

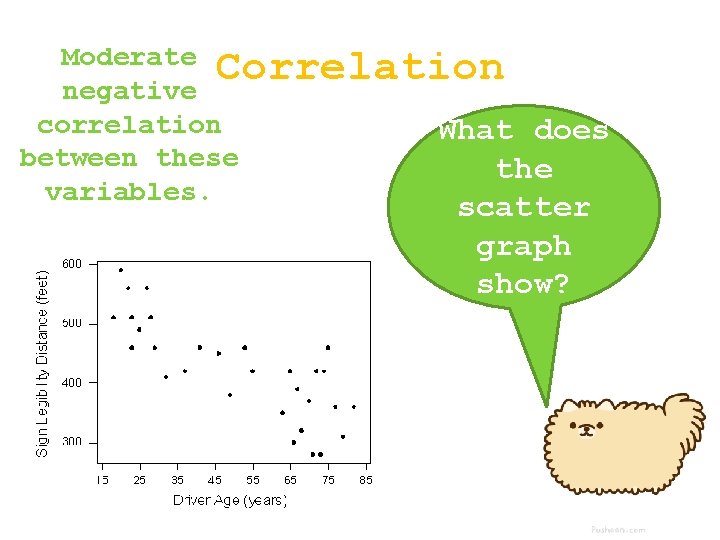
Moderate Correlation negative correlation What does between these the variables. scatter graph show?

Practice questions Answers: 1. • (a) • (b) • (c) as the diameter of the molecule increases the permeability / relative ability to move decreases (accept converse); the relationship is logarithmic / non-linear / negative; for molecules above 0. 6 (± 0. 1) nm relative ability to move changes little / for molecules below 0. 6 (± 0. 1) nm relative ability to move changes rapidly; 2 max (i) 10 mmol cm cells hr (accept values within ± 5); 1 – 3 – 1 (ii) 370 mmol cm cells hr (accept values within ± 10); (i) glucose uptake in facilitated diffusion levels out whereas uptake in simple diffusion does not level out / continues to rise; glucose uptake increases in both; glucose uptake is higher in facilitated diffusion (than in simple diffusion); glucose uptake in simple diffusion is constant / linear whereas in facilitated diffusion uptake increases rapidly at the beginning / increase is not constant; 3 max little / no change in glucose uptake; most / all (protein) channels in use; (ii) – 3 – 1 1

Practice questions Answers: 2. • (a) standard deviation summarizes the spread of values around the mean / 68% of all values fall within one standard deviation of the mean / gives a measure of variability of the data / OWTTE 1 max • (b) November had 113 (+2) ciliates ml-1 sediment (units required) • (c) production by treated and untreated samples is almost the same; production by untreated samples is usually slightly higher than treated samples; except November, January when the treated samples have a slightly higher methane production; 2 max • (d) endosymbionts do not seem to be responsible for methane production; methane production is almost the same whether the ciliates are alive (untreated samples) or killed (treated samples); no apparent correlation between methane production and number of ciliates; months when the population of ciliates is highest are not the months when the methane production is highest / ciliate numbers high in November when methane production is low / methane production highest in July and August when ciliate numbers are not high; 2 max 1

Practice questions Answers: 2. • (e) greenhouses gases collect in atmosphere; layer of gases allows incoming short-wave radiation (from sun) to pass through to earth’s surface where it is converted to longer-wave radiation; long wave radiation cannot all pass through layer of gases but some reflected back to earth causing earth’s surface to become warmer; 2 max • (f) first name / Nacella refers to the genus and the second name / concinna refers to the species 1 • (g) negative correlation / inversely proportional / as temperature increases the percentage righting in N. concinna decreases 1 • (h) percentage of N. concinna able to right themselves decrease by 50% / decreases from 95% to less than 50% / less than half able to right themselves 1 • (i) model suggests two degree rise in temperature which would mean summer temperatures of 3°C; at this temperature less than 50% of organisms able to carry out basic behaviour; decreased survival of species / decreased ability to avoid predation; 2 max