Revision The Line Basics Distance formula Midpoint formula

Revision The Line Basics Distance formula = Midpoint formula = ( , ) Slope = Equation of a line = y – y 1 = m(x – x 1)

What does the Equation of a Line do? • Tells us where on the graph the line is situated • Tells us whether a point is on or not on a line • Tells us the slope of the line The line B has an equation 3 x + 4 y = 12 (i) Find the slope of this equation (ii) Find the x-intercept and the y intercept of this line (iii) Is the point (-1, 5) on this line? (iv) The point (-4, k) is on the line, find the value of k

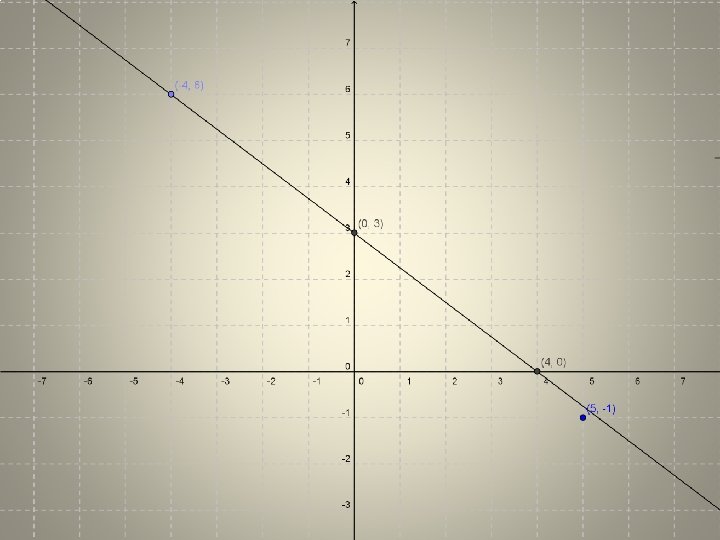
The line B has an equation 3 x + 4 y = 12 (i) Find the slope (get y on its own) 3 x + 4 y = 12 4 y = -3 x +12 y = -3 x + 12 4 4 Slope = -¾ (ii) Find y-intercept and x-intercept (another way of saying where it crosses x and y-axis) x-axis, y = 0 y-axis, x = 0 3 x + 4(0) = 12 3(0) + 4 y = 12 3 x = 12 4 y = 12 x=4 y=3 (4, 0) (0, 3) (iii) Is the point (-1, 5) on the line? (iv) The point (-4, k) IS on the line, find k Fill in the point (-4, k) Fill the point into equation 3(-4) + 4 k =12 3(-1) + 4(5) = 12 -12 + 4 k = 12 -3 + 20 = 12 4 k =24 17 ≠ 12 The point (-1, 5) is not on the line k = 6

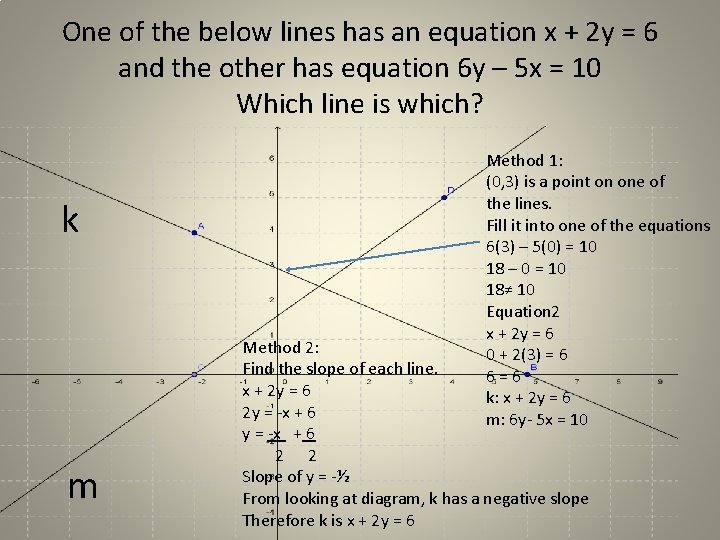
One of the below lines has an equation x + 2 y = 6 and the other has equation 6 y – 5 x = 10 Which line is which? k m Method 1: (0, 3) is a point on one of the lines. Fill it into one of the equations 6(3) – 5(0) = 10 18 – 0 = 10 18≠ 10 Equation 2 x + 2 y = 6 0 + 2(3) = 6 6=6 k: x + 2 y = 6 m: 6 y- 5 x = 10 Method 2: Find the slope of each line. x + 2 y = 6 2 y = -x + 6 2 2 Slope of y = -½ From looking at diagram, k has a negative slope Therefore k is x + 2 y = 6

Parallel and Perpendicular lines When you see either of these two words, immediately you think. . SLOPE The line D has an equation -2 x + y =4 The line E contains the point (3, 0) and is PERPINDICULAR to the line D. (i) Find the equation of the line E (ii) Find the point of intersection of D and E (iii) Find the y-intercept of E.

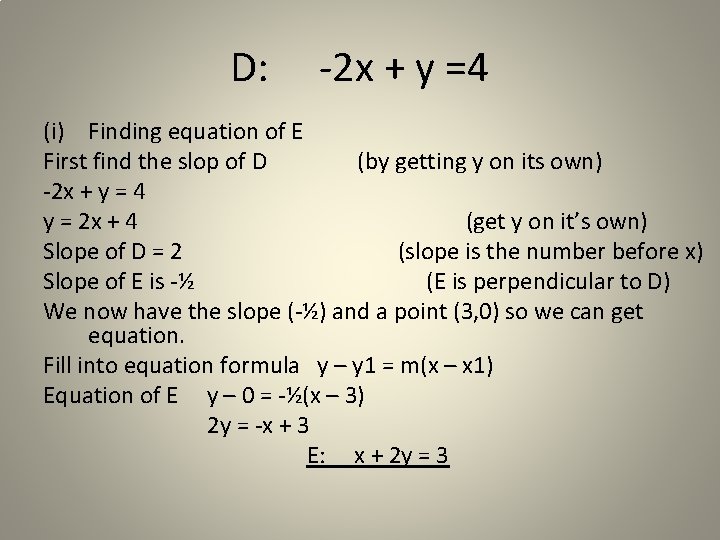
D: -2 x + y =4 (i) Finding equation of E First find the slop of D (by getting y on its own) -2 x + y = 4 y = 2 x + 4 (get y on it’s own) Slope of D = 2 (slope is the number before x) Slope of E is -½ (E is perpendicular to D) We now have the slope (-½) and a point (3, 0) so we can get equation. Fill into equation formula y – y 1 = m(x – x 1) Equation of E y – 0 = -½(x – 3) 2 y = -x + 3 E: x + 2 y = 3

Point of intersection of D and E E: D: x + 2 y = 3 -2 x + y = 4 2 x + 4 y = 6 -2 x + y = 4 5 y = 10 y=2 x = -1 (-1, 2) Y-Intercept of E When crossing the y-axis, x = 0 x + 2 y = 3 0 + 2 y = 3/2 y = 1½ (0, 1½)