Revision Statistical Data Types of Graphs Charts Tables

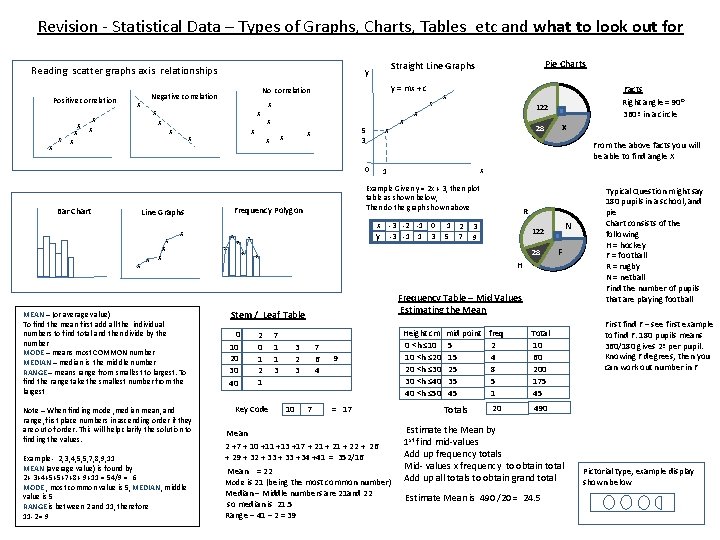
Revision - Statistical Data – Types of Graphs, Charts, Tables etc and what to look out for Reading scatter graphs axis relationships Positive correlation x x x y = mx + c No correlation Negative correlation x x x x x MEAN – (or average value) To find the mean first add all the individual numbers to find total and then divide by the number MODE – means most COMMON number MEDIAN – median is the middle number RANGE – means range from smallest to largest. To find the range take the smallest number from the largest Note – When finding mode , median mean, and range , first place numbers in ascending order if they are out of order. This will help clarify the solution to finding the values. Example - 2, 3, 4, 5, 5, 7, 8, 9, 11 MEAN (average value) is found by 2+ 3+4+5+5+7+8+ 9+11 = 54/9 = 6 MODE , most common value is 5, MEDIAN, middle value is 5 RANGE is between 2 and 11, therefore 11 -2 = 9 x x 28 -3 -2 -1 0 -3 -1 1 3 1 2 5 7 R 3 9 Key Code N 122 28 x 2 0 1 2 1 x x F H Frequency Table – Mid Values Estimating the Mean Stem / Leaf Table 0 10 20 30 40 122 1 x y x Facts Right angle = 90º 360º in a circle x Example Given y = 2 x + 3, then plot table as shown below, Then do the graph shown above Frequency Polygon Line Graphs x x From the above facts you will be able to find angle X 0 Bar Chart x x 5 3 x x x Pie Charts Straight Line Graphs y 7 1 1 3 3 2 3 10 7 6 4 7 9 = 17 Mean 2 +7 + 10 +11 +13 +17 + 21 + 22 + 26 + 29 + 32 + 33 +34 +41 = 352/16 Mean = 22 Mode is 21 (being the most common number) Median – Middle numbers are 21 and 22 so median is 21. 5 Range – 41 – 2 = 39 Height cm 0 <h ≤ 10 10 <h ≤ 20 20 <h ≤ 30 30 <h ≤ 40 40 <h ≤ 50 mid point freq 2 5 4 15 8 25 5 35 1 45 Total 10 60 200 175 45 20 490 Totals Estimate the Mean by 1 st find mid-values Add up frequency totals Mid- values x frequency to obtain total Add up all totals to obtain grand total Estimate Mean is 490 /20 = 24. 5 Typical Question might say 180 pupils in a school, and pie Chart consists of the following H = hockey F = football R = rugby N = netball Find the number of pupils that are playing football First find F – see first example to find F. 180 pupils means 360/180 gives 2º per pupil. Knowing F degrees, then you can work out number in F Pictorial type, example display shown below