Revision Index Page 2 Page 9 Page 16


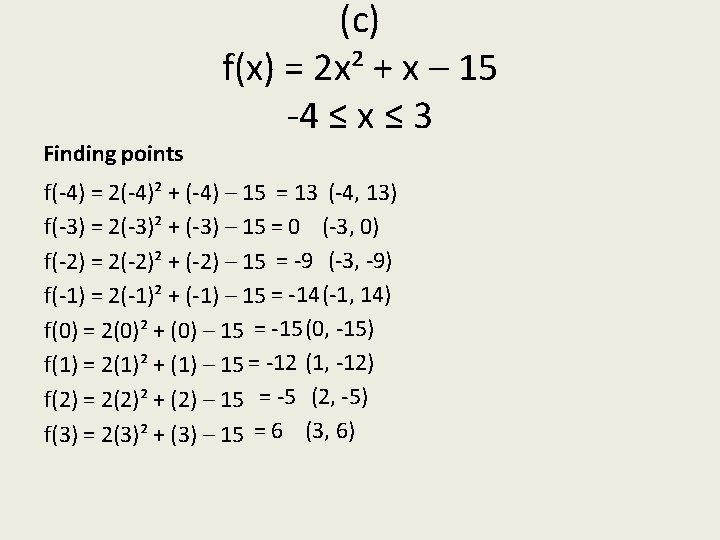








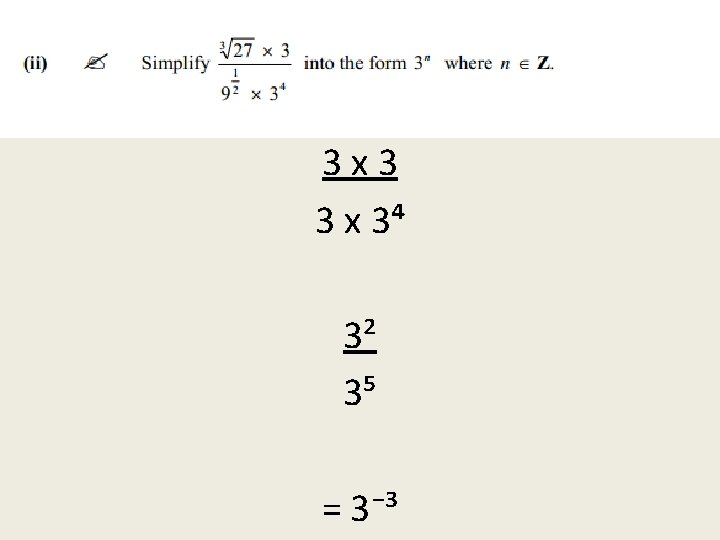















- Slides: 38

Revision Index Page 2 Page 9 Page 16 Page 20 Functions and Graphs Rules of Indices Rules of Surds Co – ordinate geometry recap

2009 Q 5 (a) “f(x) = 5 x – 12 and =a ” f(a) = 5 a – 12 a = 5 a – 12 4 a = 12 a=3 f(a)

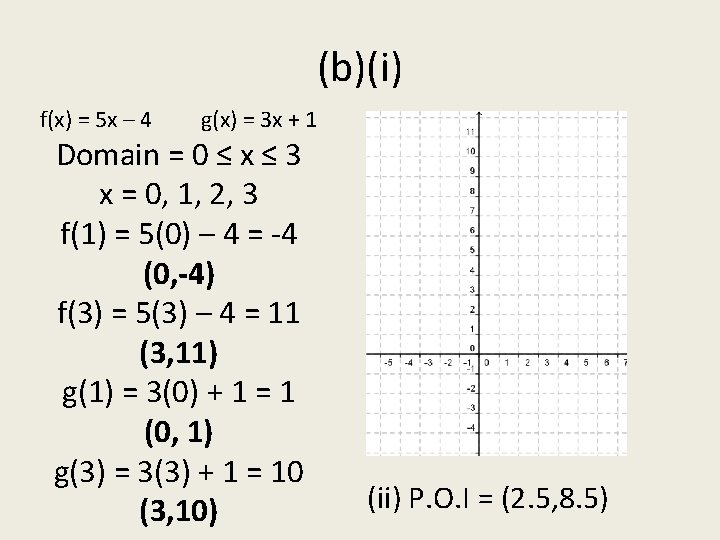
(b)(i) f(x) = 5 x – 4 g(x) = 3 x + 1 Domain = 0 ≤ x ≤ 3 x = 0, 1, 2, 3 f(1) = 5(0) – 4 = -4 (0, -4) f(3) = 5(3) – 4 = 11 (3, 11) g(1) = 3(0) + 1 = 1 (0, 1) g(3) = 3(3) + 1 = 10 (3, 10) (ii) P. O. I = (2. 5, 8. 5)
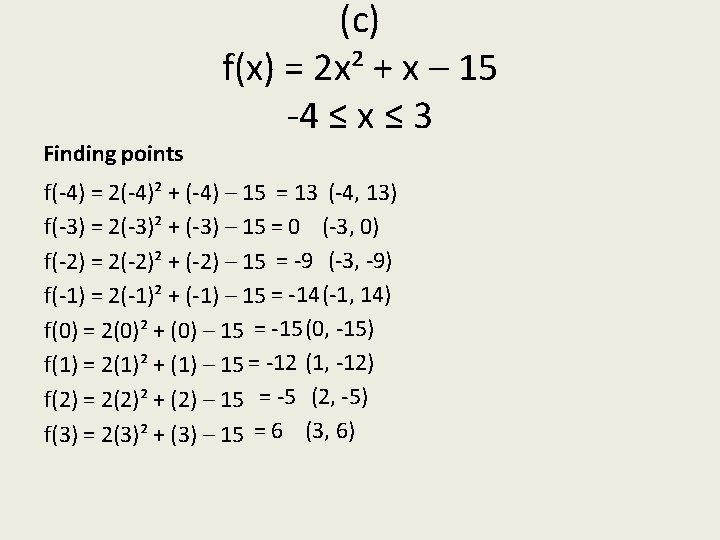

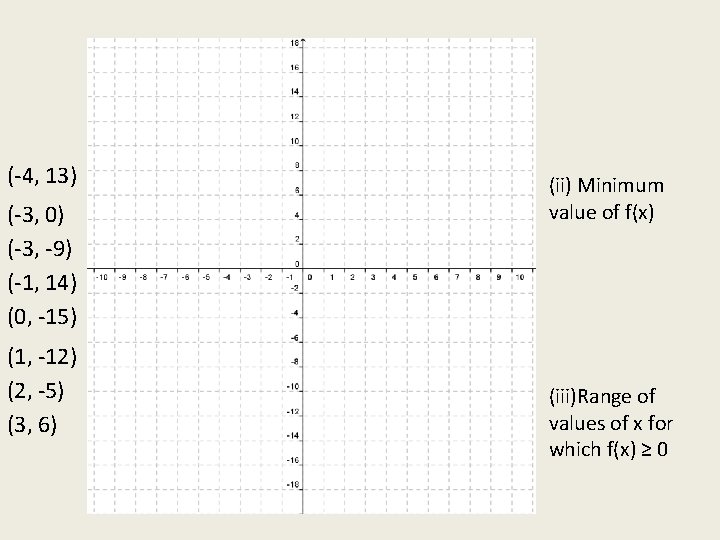
(-4, 13) (-3, 0) (-3, -9) (-1, 14) (0, -15) (1, -12) (2, -5) (3, 6) (ii) Minimum value of f(x) (iii)Range of values of x for which f(x) ≥ 0

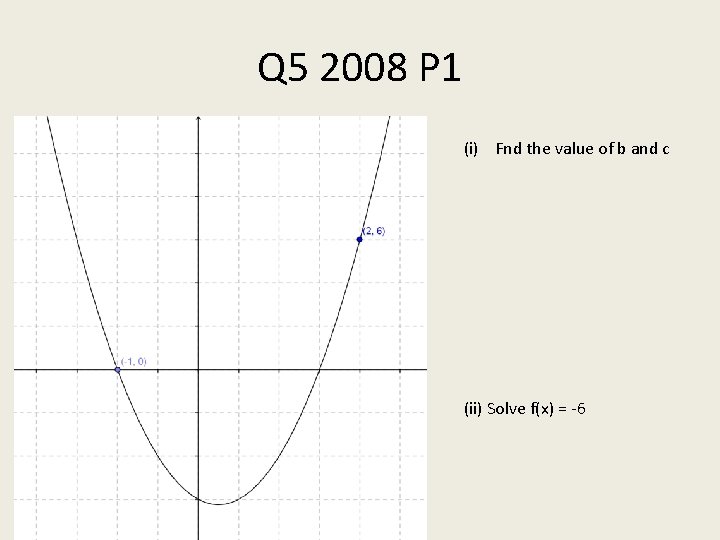
Q 5 2008 P 1 (i) Fnd the value of b and c (ii) Solve f(x) = -6

2007 P 1 (a) Express 72 km/hr in metres per second 1000 m = 1 km 72 km/hr = 72, 000 m/hr 60 mins in 1 hour 3600 seconds in 1 hour 72, 000 ÷ 3, 600 = 20 m/s

(ii) Snowman with mass of 12 kg Melts at a rate of 0. 2% of its mass per minute What is its mass after 3 mins Mass at start of 1 st min: Less 0. 2% Mass after 1 min 12 kg 0. 024 kg 11. 976 kg Mass at start of 2 nd min: Less 0. 2% Mass after 2 mins 11. 976 0. 23952 kg 11. 952 kg Mass at start of 3 rd min: Less 0. 2% Mass after 3 mins 11. 952 0. 23904 kg 11. 928 kg Mass after 3 min = 11. 93 kg

(c) Indices Rules of Indices an x a m = a n + m an/am = an – m Rule 2: (4³)² = 4⁶ Example: 4⁶ x 4³ = 4⁹ 5⁷ 5⁵ = 5² Example: Express 9⁴ in the form 3 n 9 = 3² 9⁴ = (3²)⁴ 9⁴ = 3⁸

Exercise Express the following in 2 n: 8² x 4³ (2³)² x (2²)³ 2⁶ x 2⁶ = 2¹² Express the following in 5 n: 25⁶ 125³ (5²)⁶ (5³)³ 5¹² 5⁹ = 5³

Rule 3 a½ = √a Example: 16½ =4 Similarly: a⅓ = ³√a Eg. 27⅓ =3

2006 3(a) paper 1 (i) (64)³⁄₂ (64½)³ 8³ = 512 (ii) (64)⅔ (64¹⁄₃)² 4² = 16 2005 3(a) paper 1 in the form 2 k = 16⅓ = (2³)⅓ = 2³⁄₃ = 2¹ k=1

we want to change everything to 2 ½ 64 ²⁄₃ 2⁵ x (2³) = √ 64 2³ x (2²)² =8 = 2³ 2⁵ x 2² 2³ x 2⁴ 2⁷ 2⁷ = 2⁰ (2³)²⁄₃ = 2⁶⁄₃ = 2² Using Calculator 2⁵ x 8²⁄₃ 64½ x 4² 32 x 4 8 x 16 128 =1 = 2⁰

2003 Q 2(b) ¼ + 8² + √ 16 ¼ + 64 + 4 = 68¼ 0. 272479 + 62. 41 + 4. 0398 66. 72228 = 66. 72
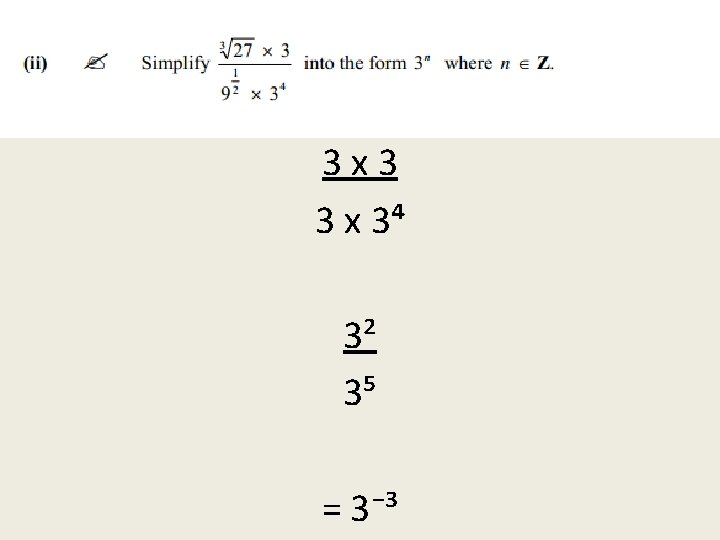

Surds Rules of Surds: √ab = √a x √b Example: √ 5 x √ 3 √ 15 Simplifying Surds: Simplify the following surd – √ 45 √ 15 x √ 3 ? √ 5 x √ 9 = 3√ 5

Express in their simplest form √ 32 √ 16 x √ 2 4√ 2 √ 18 √ 75 √ 9 x √ 2 3√ 2 √ 25 x √ 3 5√ 3 Hint: √ 3(3 √ 2) 3√ 6 5√ 2(4√ 5) 20√ 10 √ 20 √ 4 x √ 5 2√ 5 Also: 4√ 3 + 6√ 3 = 10√ 3



Coordinate Geometry (Paper 2 Q 2) What you can be asked Basic Formulae: Distance Midpoint Slope Years they come up 2011, 2010, 2008, 2006 2010, 2009, 2008, 2007 2011, 2007, 2005 Important Formula: Equation of a line 2011, 2008, 2007, 2006, - we need a point 2005 - and the slope Other Basics: Getting slope of a line from the equation 2010 Showing that a certain point is on a line 2009, 2008, 2007, 2005

More complex questions Years Parallel/perpendicular Lines - as soon as you see this word you think SLOPE 2011, 2010, Crossing the x-axis: - As soon as you see this you think “when crossing the x – axis, y = 0” - Vica versa with y-axis Point of intersection - Very easy with a graph - use simultaneous equations otherwise 2009, 2007, 20 06, 2005(b)(iv) 2011, 2008, 20 07 2010, 2007, 2006, 2005

Ctd. Symmetry: - axial - central - transformation Years they come up 2011, 2004, 2003 Showing Lines on a graph: 2009, 2008 Other: - Finding the area of a triangle on the graph 2010, 2009, 2008

2005 Q 2 (a) a(1, 4) and b(-2, -1) (x 1, y 1) (i) Slope of ab (x 2, y 2) (ii) Equation of ab y – y 1 = m(x – x 1) y – 4 = ⁵⁄₃(x – 1) 3(y – 4) = 5(x – 1) 3 y – 12 = 5 x – 5 3 y – 5 x = 7

(b) L is the line 3 x – 4 y + 7 = 0 Contains(-1, h) M is the line 4 x + 3 y -24 = 0 and contains point (k, 0) (i) Find h and k 3 x – 4 y + 7 = 0 3(-1) – 4(h) + 7 = 0 -3 – 4 h + 7 = 0 -4 h = -4 h=1 (i) Find h and k 4 x + 3 y -24 = 0 4(k) + 3(0) -24 = 0 4 k – 24 = 0 4 k = 24 k=6

(b) L is the line 3 x – 4 y + 7 = 0 Contains(-1, h) M is the line 4 x + 3 y -24 = 0 and contains point (k, 0) (ii) Point of intersection of L and M is r 3 x – 4 y = -7 x=3 4 x + 3 y = 24 3 x – 4 y = -7 3(3) – 4 y = -7 9 x – 12 y = -21 16 x + 12 y = 96 y = 4 25 x = 75 P. O. I = (3, 4) x=3

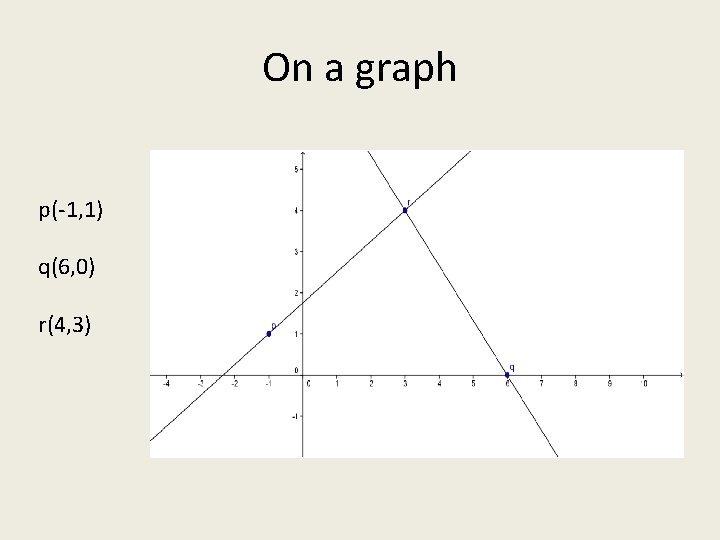
On a graph p(-1, 1) q(6, 0) r(4, 3)

Prove it’s a Right Angle If it’s a right angle – the lines are perpendicular i. e. their slopes multiplied give you -1 Slope of L: 3 x – 4 y + 7 = 0 -b/a = -(-4)/3 m₁= ⁴⁄₃ Slope of M: 4 x + 3 y – 24 = 0 -b/a = -3/4 = m₂ = -¾ ⁴⁄₃ x (-¾) = -1

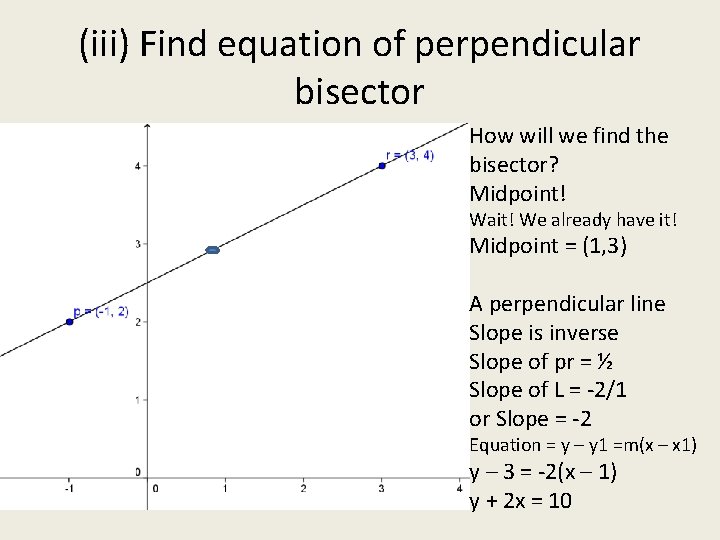
2006(b) p(-1, 2) r(3, 4) (i)Midpoint = (1, 3) (ii) Slope = 2/4 m=½

(iii) Find equation of perpendicular bisector How will we find the bisector? Midpoint! Wait! We already have it! Midpoint = (1, 3) A perpendicular line Slope is inverse Slope of pr = ½ Slope of L = -2/1 or Slope = -2 Equation = y – y 1 =m(x – x 1) y – 3 = -2(x – 1) y + 2 x = 10

(iv) Equation of K is x – 2 y = 0 Point of intersection L: y + 2 x = 5 K: -2 y + x = 0 2 y + 4 x = 10 -2 y + x = 0 5 x = 10 x=2 y + 2 x = 5 y+8=5 y=1 Point of Intersection= (2, 1)

Trigonometry 2006 Paper 2 Q 5 (a) Construct the angle A such that Tan A = ¾ Tan = opposite/adjacent We construct a right angled triangle where the opposite side is 3 and the adjacent is 4 3 A 4

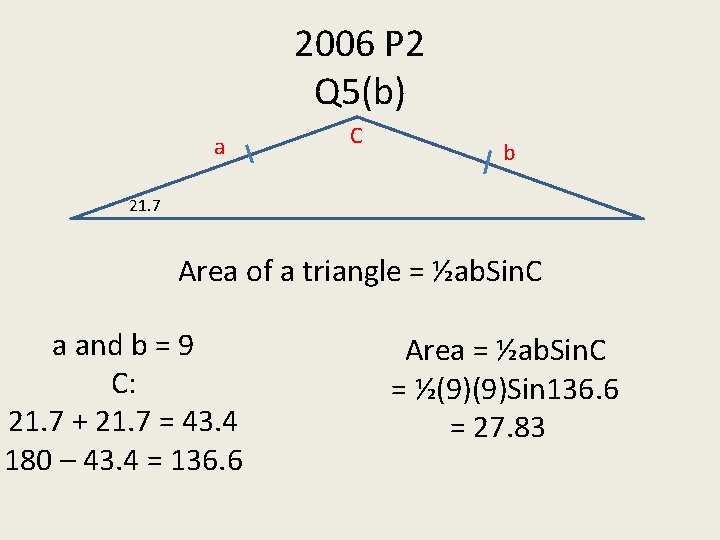
2006 P 2 Q 5(b) a C b 21. 7 Area of a triangle = ½ab. Sin. C a and b = 9 C: 21. 7 + 21. 7 = 43. 4 180 – 43. 4 = 136. 6 Area = ½ab. Sin. C = ½(9)(9)Sin 136. 6 = 27. 83

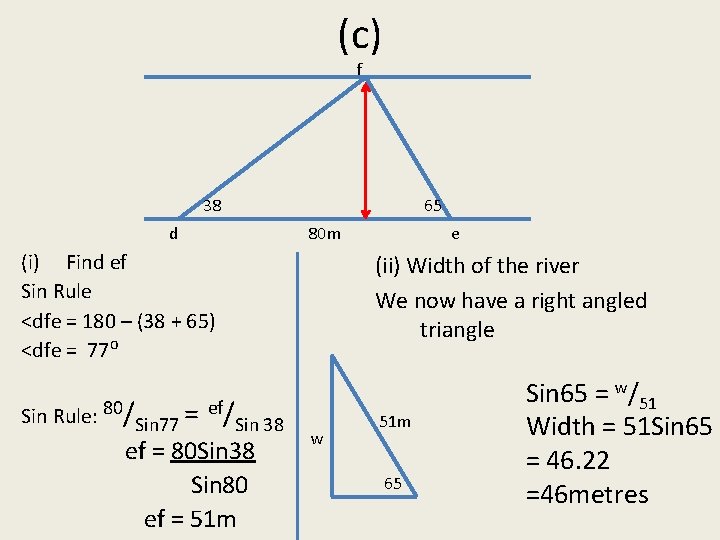
(c) f 38 d 65 80 m (i) Find ef Sin Rule <dfe = 180 – (38 + 65) <dfe = 77⁰ Sin Rule: 80/Sin 77 = ef/Sin 38 ef = 80 Sin 38 Sin 80 ef = 51 m e (ii) Width of the river We now have a right angled triangle w 51 m 65 Sin 65 = w/51 Width = 51 Sin 65 = 46. 22 =46 metres

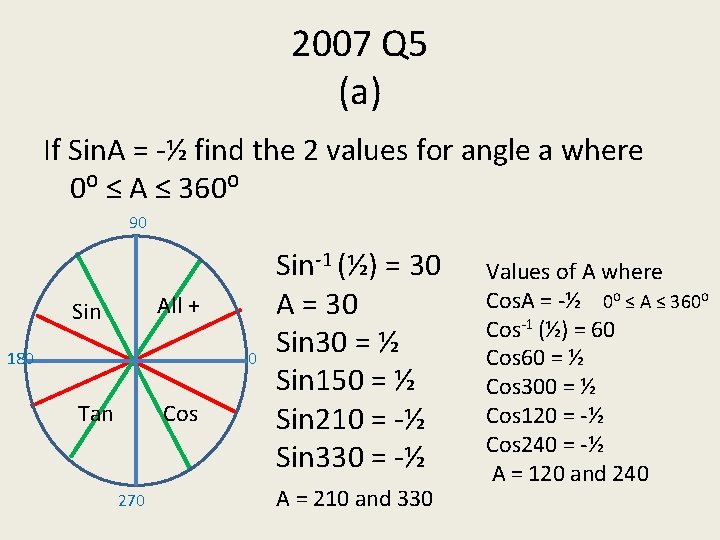
2007 Q 5 (a) If Sin. A = -½ find the 2 values for angle a where 0⁰ ≤ A ≤ 360⁰ 90 All + Sin 180 0 Tan Cos 270 Sin-1 (½) = 30 A = 30 Sin 30 = ½ Sin 150 = ½ Sin 210 = -½ Sin 330 = -½ A = 210 and 330 Values of A where Cos. A = -½ 0⁰ ≤ A ≤ 360⁰ Cos-1 (½) = 60 Cos 60 = ½ Cos 300 = ½ Cos 120 = -½ Cos 240 = -½ A = 120 and 240

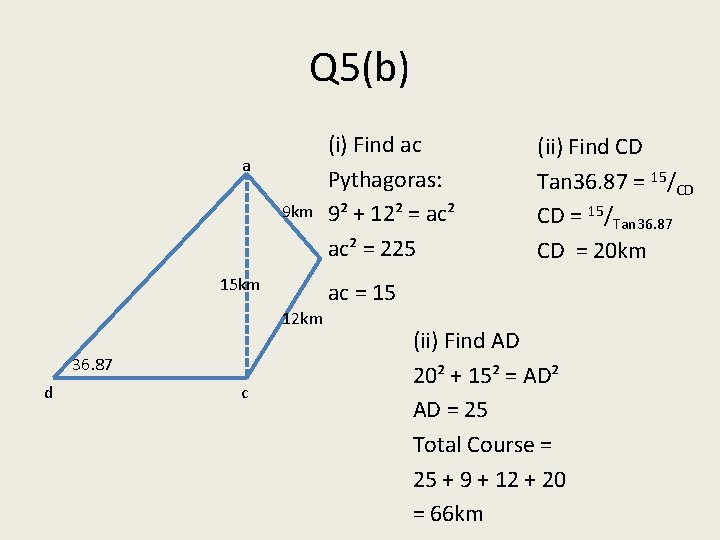
Q 5(b) a 9 km 15 km d c (ii) Find CD Tan 36. 87 = 15/CD CD = 15/Tan 36. 87 CD = 20 km ac = 15 12 km 36. 87 (i) Find ac Pythagoras: 9² + 12² = ac² = 225 (ii) Find AD 20² + 15² = AD² AD = 25 Total Course = 25 + 9 + 12 + 20 = 66 km

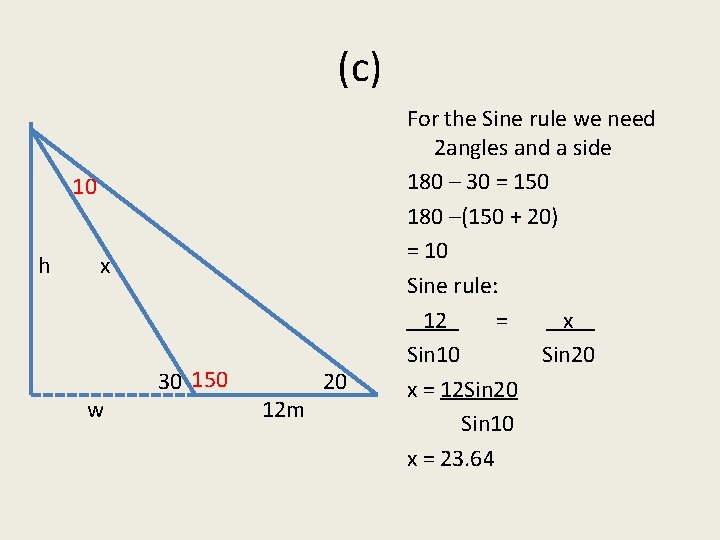
(c) 10 h x w 30 150 12 m 20 For the Sine rule we need 2 angles and a side 180 – 30 = 150 180 –(150 + 20) = 10 Sine rule: 12 = x Sin 10 Sin 20 x = 12 Sin 20 Sin 10 x = 23. 64

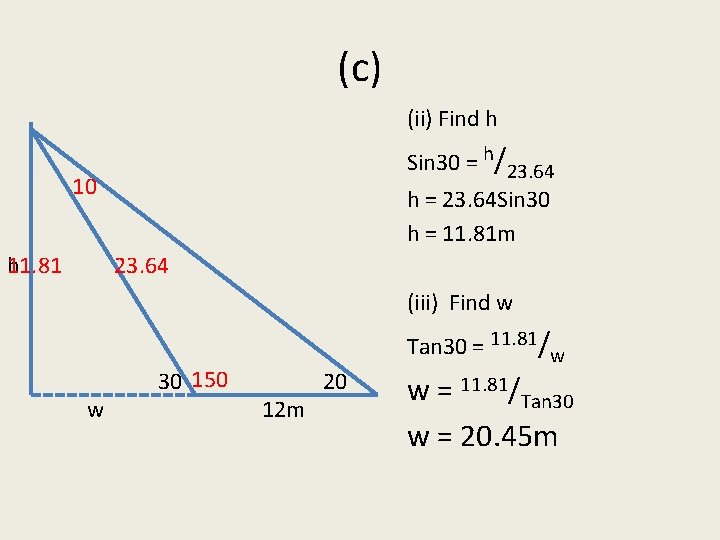
(c) (ii) Find h Sin 30 = h/23. 64 10 h 11. 81 h = 23. 64 Sin 30 h = 11. 81 m 23. 64 (iii) Find w w 30 150 12 m 20 Tan 30 = 11. 81/w w = 11. 81/Tan 30 w = 20. 45 m

 Passive revision
Passive revision Simplify a½ • a⅓
Simplify a½ • a⅓ Clustered index và non clustered index
Clustered index và non clustered index Diff between step index and graded index fiber
Diff between step index and graded index fiber Single mode fiber supports meridional rays
Single mode fiber supports meridional rays Dense secondary index
Dense secondary index Simpsons diversity index equation
Simpsons diversity index equation Morphological index
Morphological index Liquid limit of soil formula
Liquid limit of soil formula Compare india and sri lanka on the basis of hdi
Compare india and sri lanka on the basis of hdi Design process index page
Design process index page Il sogno palm desert
Il sogno palm desert Hello hello 1 2 3
Hello hello 1 2 3 Index.php?page= site:com
Index.php?page= site:com Index front page
Index front page Cover page apa format
Cover page apa format Cornu plural
Cornu plural Gcse pe revision booklet
Gcse pe revision booklet Alan spence sailmaker
Alan spence sailmaker Solid edge revision manager
Solid edge revision manager Themes of a christmas carol
Themes of a christmas carol Present tenses revision
Present tenses revision Biopsychology revision
Biopsychology revision Eft revision task
Eft revision task Red bull revision
Red bull revision Year 9 maths revision booklet
Year 9 maths revision booklet Fsmq
Fsmq Higher computing revision
Higher computing revision Wjec criminology unit 4
Wjec criminology unit 4 Revision unit 1
Revision unit 1 Geometría capítulo 7 revisión respuestas
Geometría capítulo 7 revisión respuestas Igcse english revision
Igcse english revision Tysk revision
Tysk revision Revision quotes
Revision quotes How useful is this source
How useful is this source Name of the image
Name of the image Past simple affirmative regular verbs
Past simple affirmative regular verbs Revision passive voice answer
Revision passive voice answer Revision verb form
Revision verb form