Revision Class Edited by Mohd Azrik PERT AND

Revision Class Edited by : Mohd Azrik

PERT AND CPM NETWORKS

Building the Network • Activity on Node (AON) Network • Activity on Arrow (AOA) Network

AON vs AOA AON AOA Nodes represented the activities Activities are shown on the arrows Easy to draw Generally more difficult Do not require dummy activity Sometime require dummy activity Used by most popular project management software (Microsoft project, etc) Use by some project management

Table 5 -1 A Sample Set of Project Activities and Precedences

Figure 5 -3 A Completed Sample AON Network Task Predecessor a b c d e f g a b b c, d e

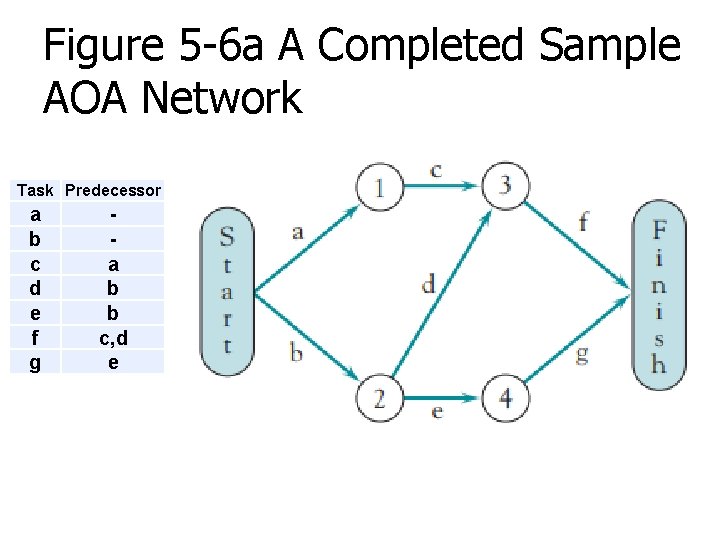
Figure 5 -6 a A Completed Sample AOA Network Task Predecessor a b c d e f g a b b c, d e

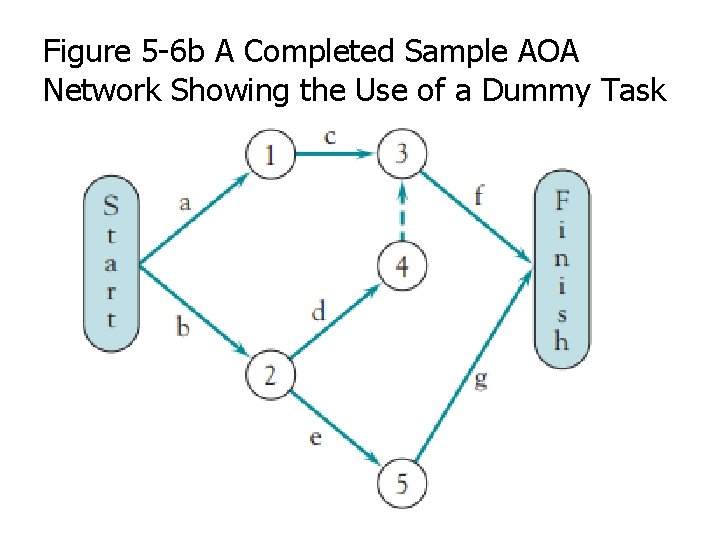
Figure 5 -6 b A Completed Sample AOA Network Showing the Use of a Dummy Task

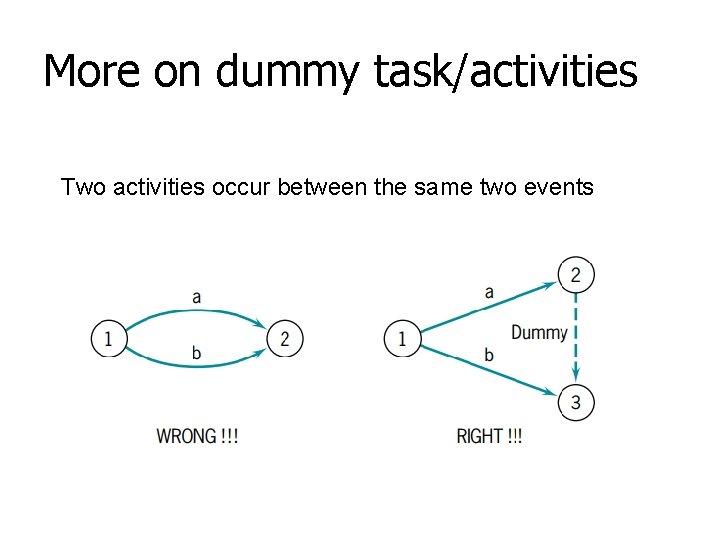
More on dummy task/activities Two activities occur between the same two events

More on dummy task/activities a, b, and c must precede activity d, but only a and b must precede activity e.

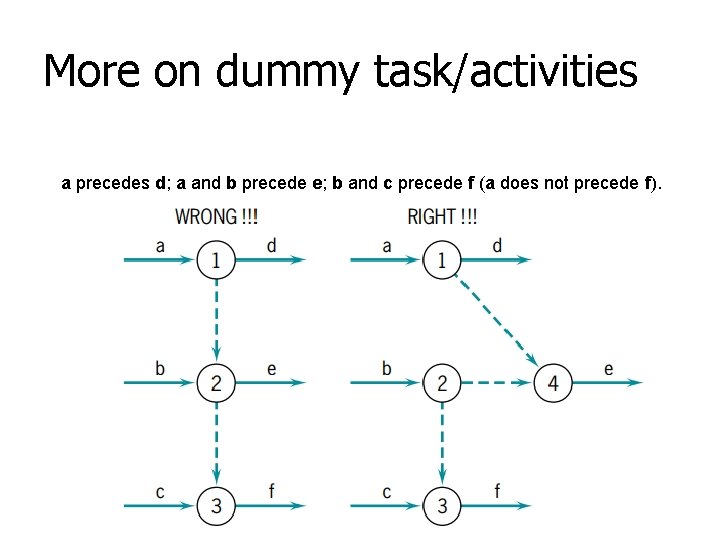
More on dummy task/activities a precedes d; a and b precede e; b and c precede f (a does not precede f).

Exercise 1 • Draw the AON and AOA diagram for the following project activities

Table 5 -2 A Sample Problem for Finding the Critical Path and Critical Time

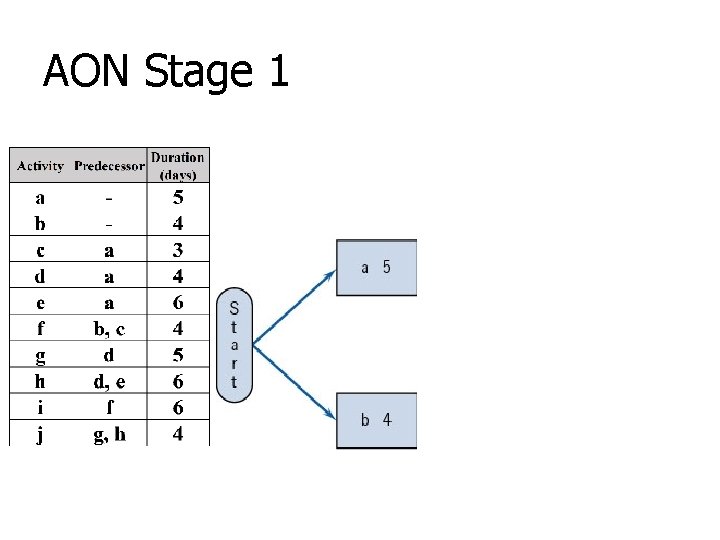
AON Stage 1

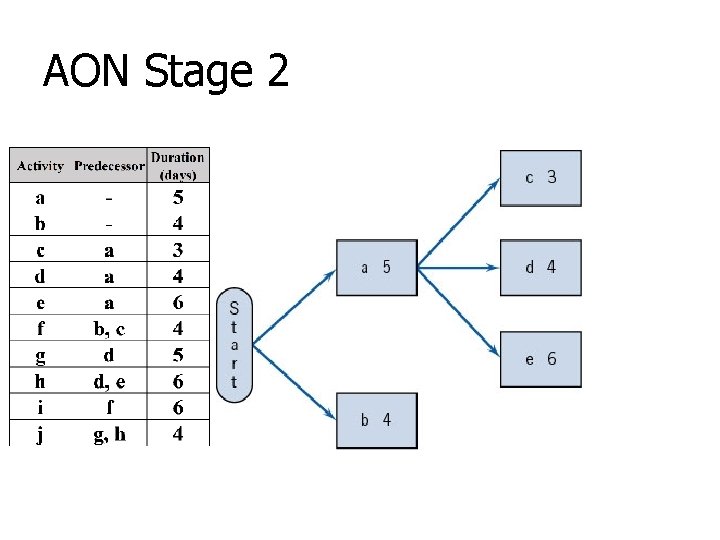
AON Stage 2

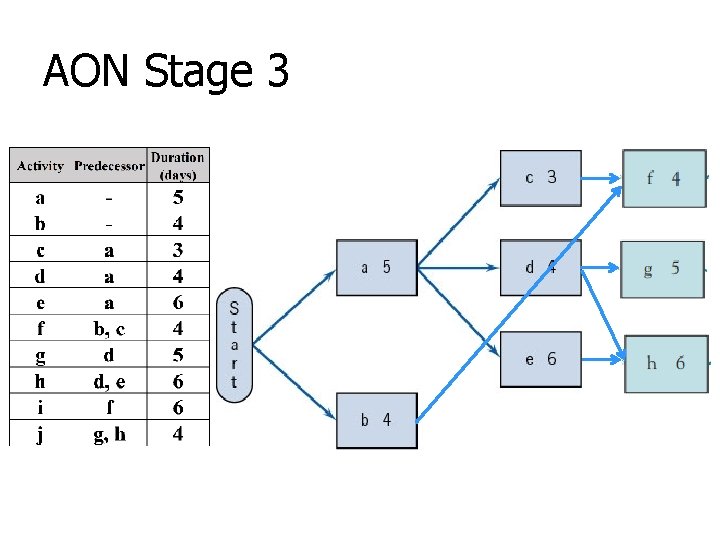
AON Stage 3

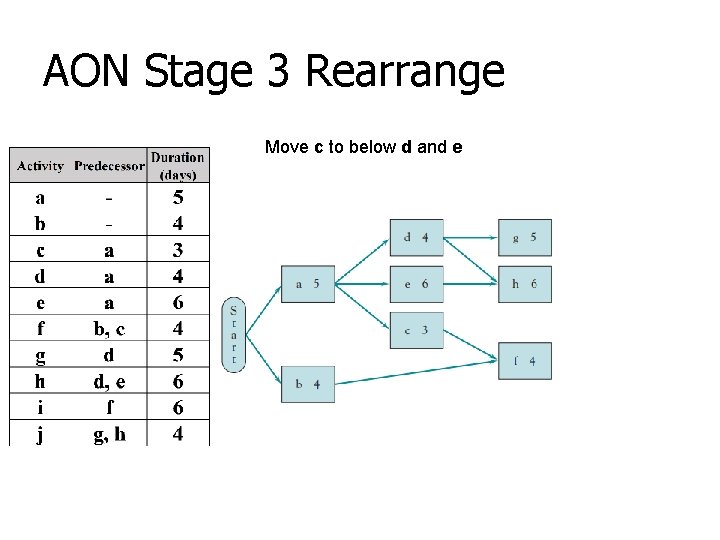
AON Stage 3 Rearrange Move c to below d and e

AON Stage 4

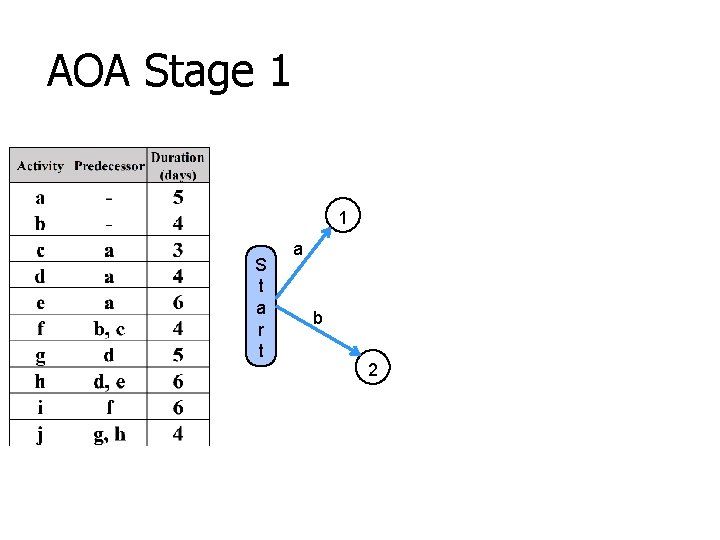
AOA Stage 1 1 S t a r t a b 2

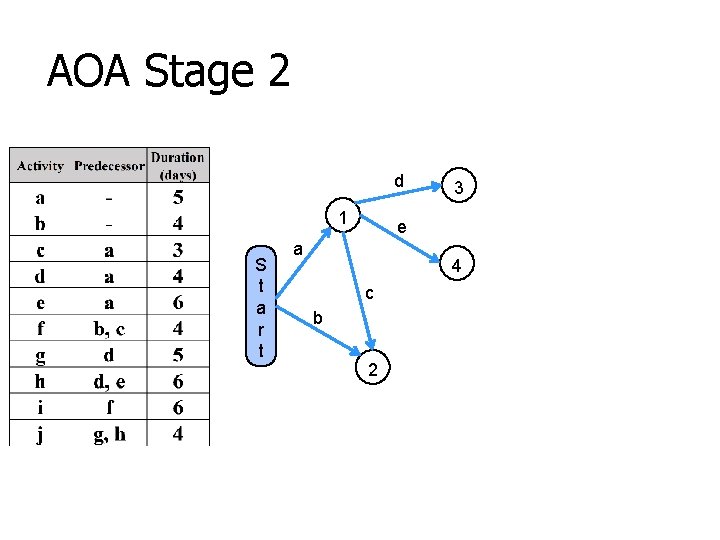
AOA Stage 2 d 1 S t a r t 3 e a 4 c b 2

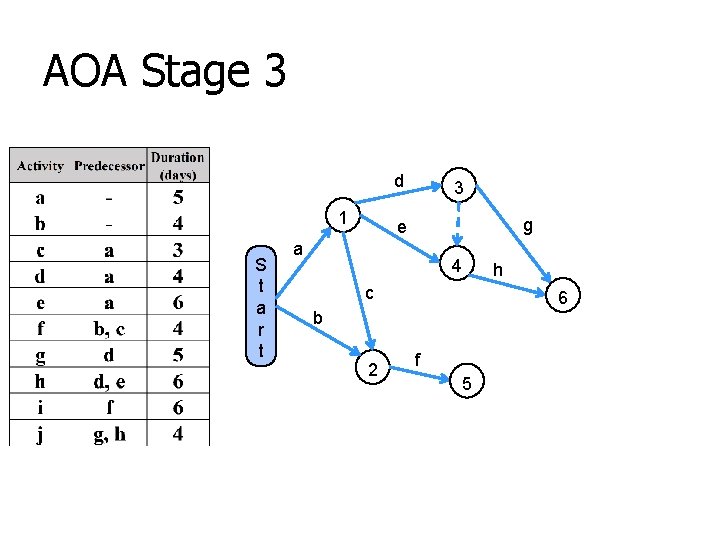
AOA Stage 3 d 1 S t a r t 3 g e a 4 c 6 b 2 h f 5

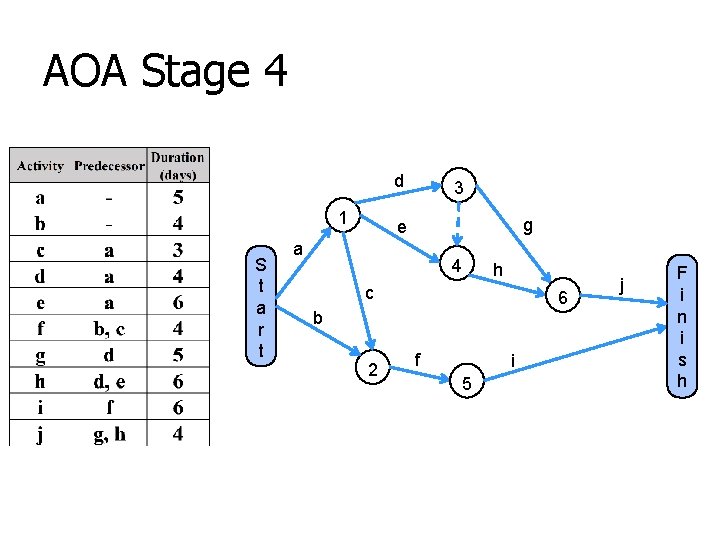
AOA Stage 4 d 1 S t a r t 3 g e a 4 h c 6 b 2 f i 5 j F i n i s h

A Complete Network AON AOA

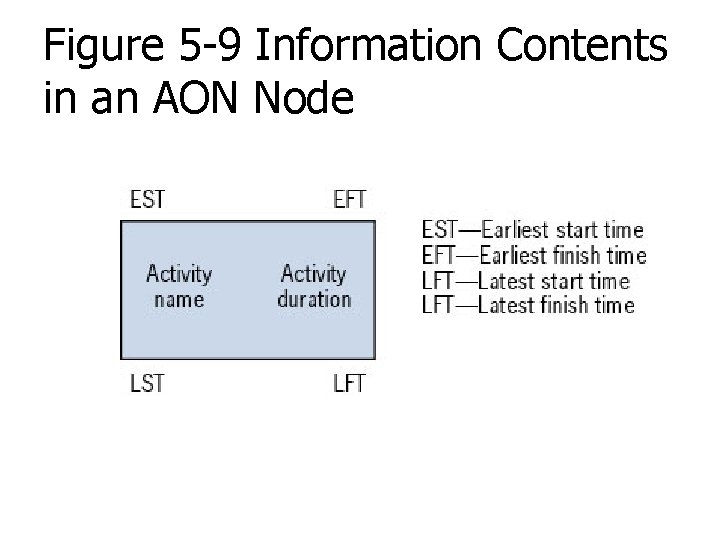
Figure 5 -9 Information Contents in an AON Node

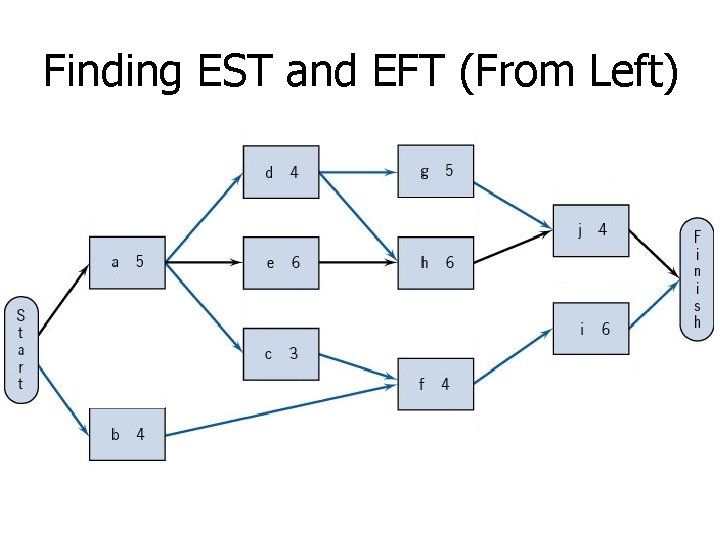
Finding EST and EFT (From Left)

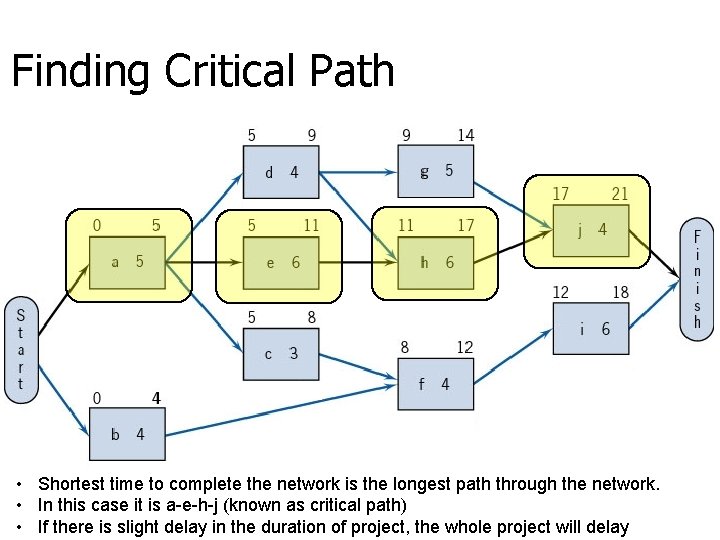
Finding Critical Path • Shortest time to complete the network is the longest path through the network. • In this case it is a-e-h-j (known as critical path) • If there is slight delay in the duration of project, the whole project will delay

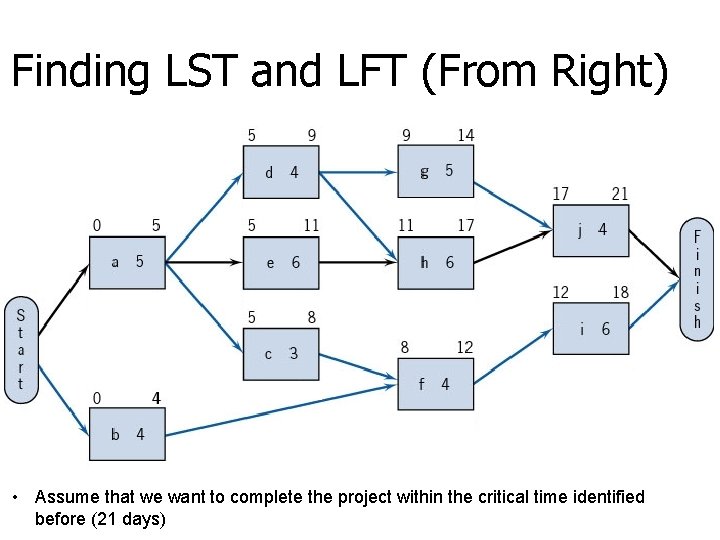
Finding LST and LFT (From Right) • Assume that we want to complete the project within the critical time identified before (21 days)

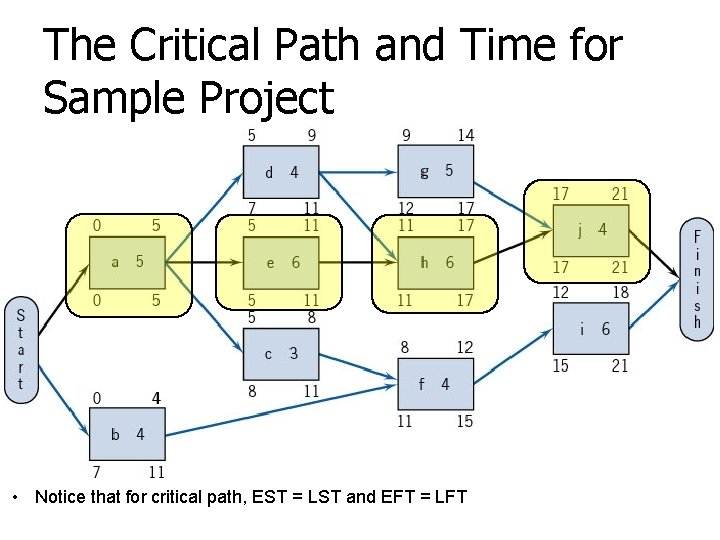
The Critical Path and Time for Sample Project • Notice that for critical path, EST = LST and EFT = LFT

Calculating Activity Slack • Slack or Float – The amount of time the non-critical activities can be delayed without delaying the project LST - EST = LFT - EFT = Slack • Remember that for critical path EST=LST so slack is 0. It mean the activities in critical path cannot be delayed.

Total float vs Free Float • Total Float: The total amount of time that a schedule activity may be delayed from its early start date without delaying the project finish date, or violating a schedule constraint. • Free Float: The amount of time that a schedule activity can be delayed without delaying the early start date of any immediately following schedule activities.

Total float vs Free Float Total Float = LST - EST = LFT - EFT = Slack Free Float = EST (of next activity) - EFT

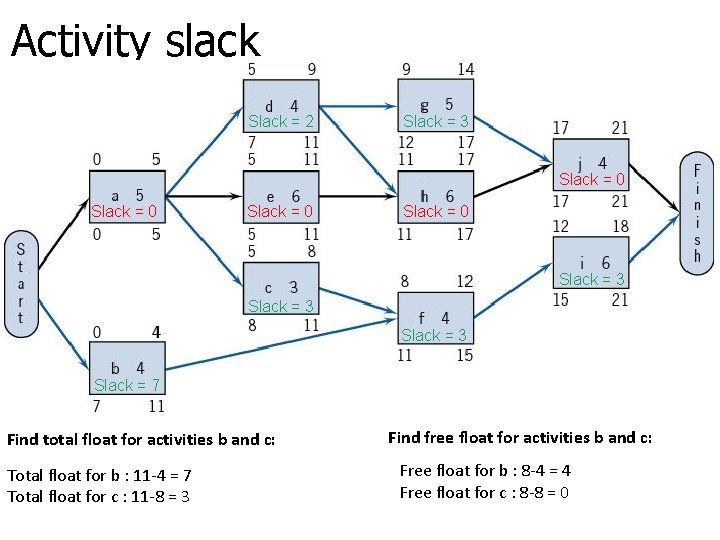
Activity slack Slack = 2 Slack = 3 Slack = 0 Slack = 3 Slack = 7 Find total float for activities b and c: Total float for b : 11 -4 = 7 Total float for c : 11 -8 = 3 Find free float for activities b and c: Free float for b : 8 -4 = 4 Free float for c : 8 -8 = 0

PROJECT UNCERTAINTY AND RISK MANAGEMENT

Calculating Probabilistic Activity Times • Three Time Estimates – optimistic (a) • Fastest possible time needed to complete an activity – most likely (m) • Normal time – pessimistic (b) • Slowest time to complete an activity

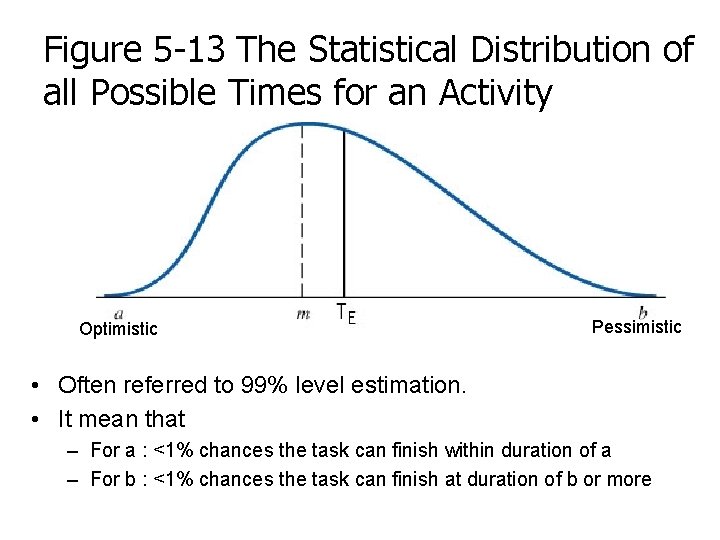
Figure 5 -13 The Statistical Distribution of all Possible Times for an Activity Optimistic Pessimistic • Often referred to 99% level estimation. • It mean that – For a : <1% chances the task can finish within duration of a – For b : <1% chances the task can finish at duration of b or more

Activity Expected Time and Variance Expected time (mean): Standard deviation: Variance:

Activity Expected Time and Variance (example) Expected time (mean): Variance:

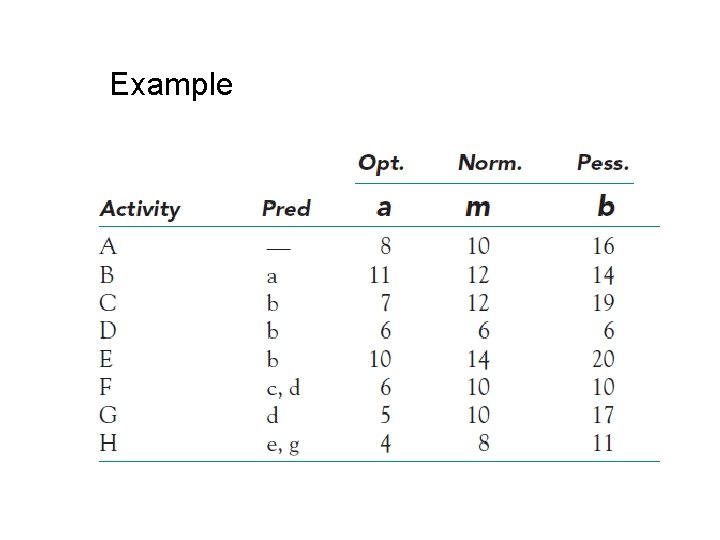
Example

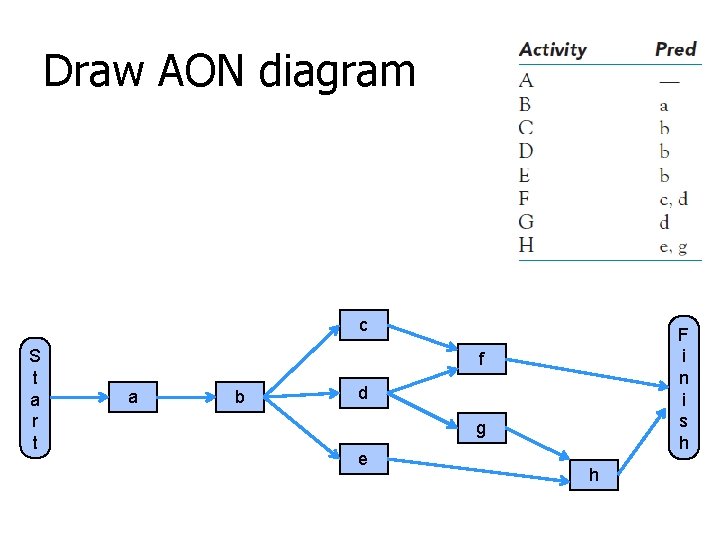
Draw AON diagram c S t a r t F i n i s h f a b d g e h

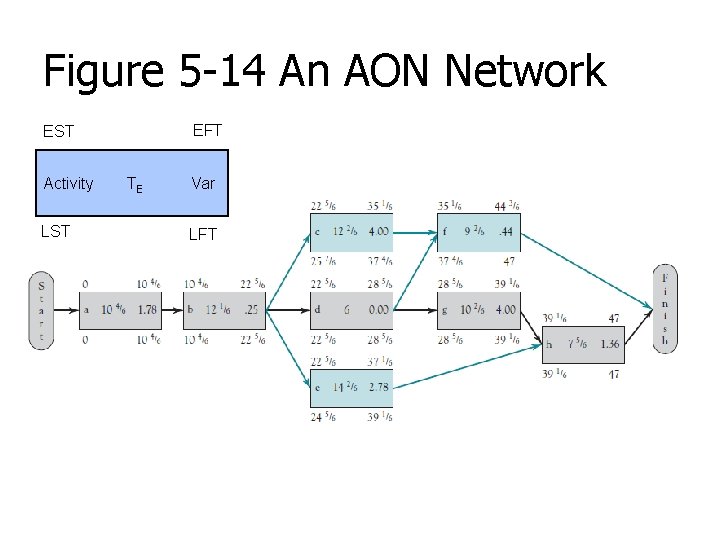
Figure 5 -14 An AON Network EFT EST Activity LST TE Var LFT

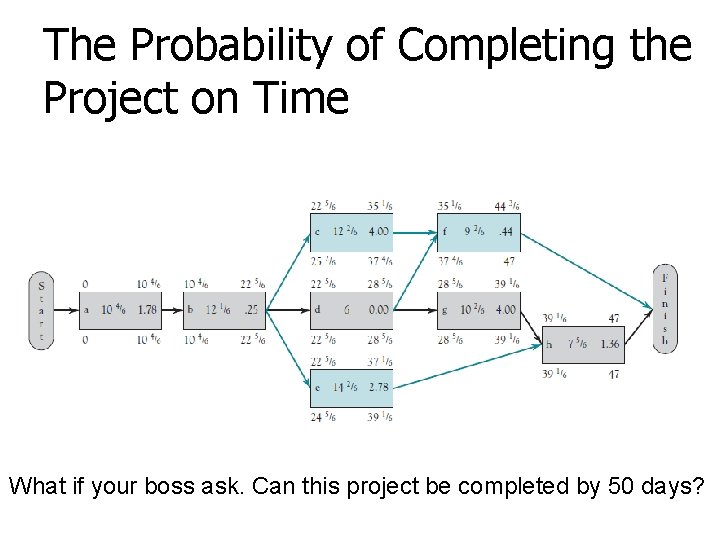
The Probability of Completing the Project on Time What if your boss ask. Can this project be completed by 50 days?

The Probability of Completing the Project on Time =NORMDIST(D, , , TRUE)

• We can start by finding Z for the critical path a-b-d-g-h

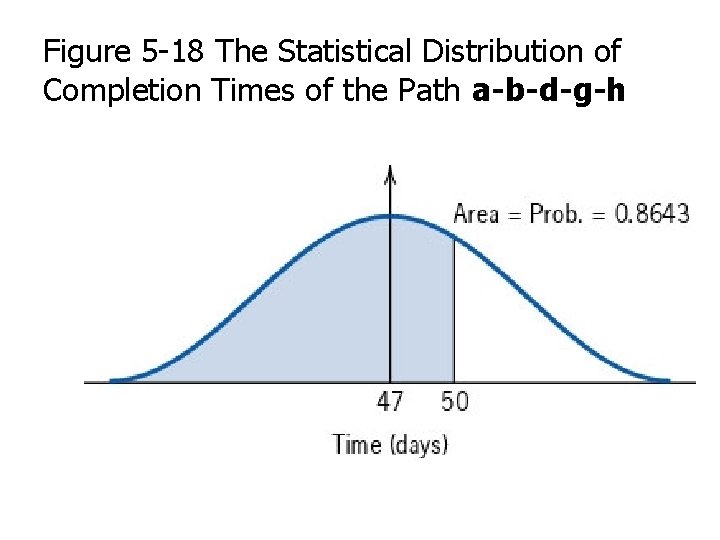
Figure 5 -18 The Statistical Distribution of Completion Times of the Path a-b-d-g-h

Cont. • The probability that the project finish less than 2 days before the expected duration D= 47 -2 = 45 days Z= (45 -47) / 2. 719 = -0. 74

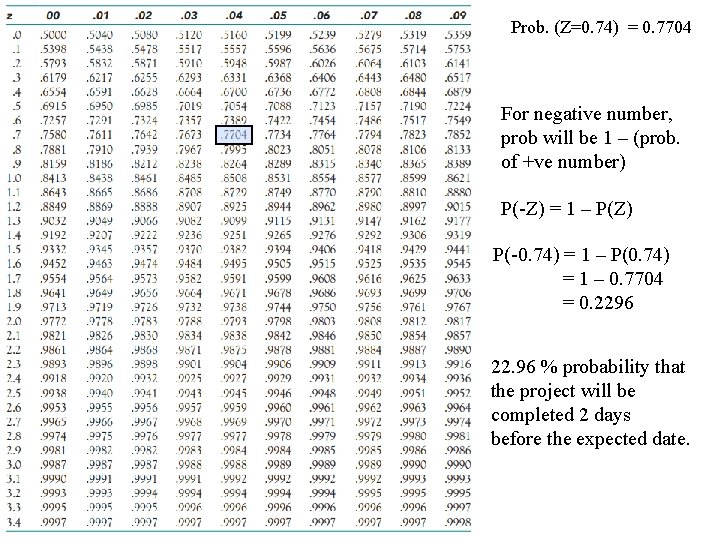
Prob. (Z=0. 74) = 0. 7704 For negative number, prob will be 1 – (prob. of +ve number) P(-Z) = 1 – P(Z) P(-0. 74) = 1 – P(0. 74) = 1 – 0. 7704 = 0. 2296 22. 96 % probability that the project will be completed 2 days before the expected date.