Revised 12600 Sorting Merge Sort Cmput 115 Lecture

Revised 1/26/00 Sorting - Merge Sort Cmput 115 - Lecture 12 Department of Computing Science University of Alberta ©Duane Szafron 2000 Some code in this lecture is based ©Duane Szafron 1999 on code from the book: Java Structures by Duane A. Bailey or the companion structure package

About This Lecture l In this lecture we will learn about a sorting algorithm called the Merge Sort. l We will study its implementation and its time and space complexity. ©Duane Szafron 1999 2

Outline l The Merge Sort Algorithm l Merge Sort - Arrays l Time and Space Complexity of Merge Sort ©Duane Szafron 1999 3

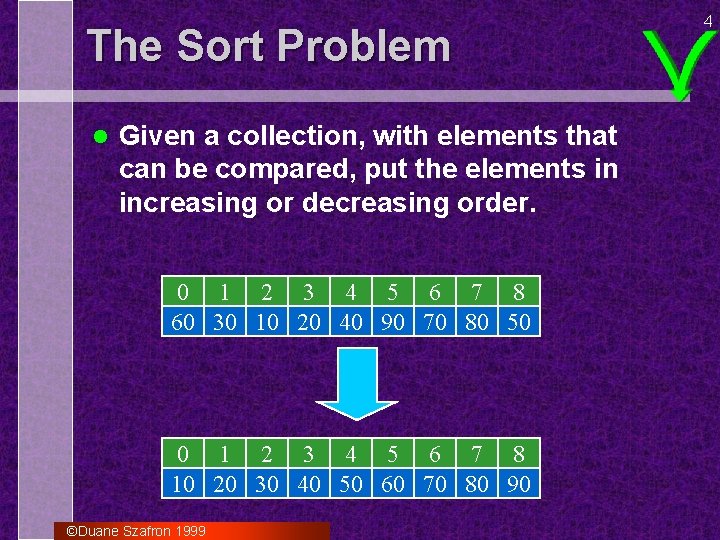
The Sort Problem l Given a collection, with elements that can be compared, put the elements in increasing or decreasing order. 0 1 2 3 4 5 6 7 8 60 30 10 20 40 90 70 80 50 0 1 2 3 4 5 6 7 8 10 20 30 40 50 60 70 80 90 ©Duane Szafron 1999 4

5 Merge Sort Algorithm - Splitting l Split the list into two halves: the bottom part and the top part. 0 1 2 3 4 5 6 7 8 60 30 10 20 40 90 70 80 50 l Make a recursive call to Merge Sort for each half. 0 1 2 3 10 20 30 60 ©Duane Szafron 1999 4 5 6 7 8 40 50 70 80 90

6 Merge Sort Algorithm - Merging l Merge the bottom sorted half and the top sorted half into a sorted whole using a Merge algorithm 0 1 2 3 10 20 30 60 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 5 6 7 8 10 20 30 60 40 50 70 80 90 ©Duane Szafron 1999

7 Merge Algorithm 0 The Merge algorithm requires temporary storage, the same size as the collection. l Before a merge, we place each subcollection in its own collection. l 0 1 2 3 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 10 20 30 60 ©Duane Szafron 1999 5 6 7 8

8 Merge Algorithm 1 l Copy the smallest from the two collections. 0 1 2 3 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 10 20 30 60 0 1 10 2 3 6 7 8 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 10 20 30 60 ©Duane Szafron 1999 5 5 6 7 8

9 Merge Algorithm 2 l Copy the smallest from the two collections. 0 1 10 2 3 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 10 20 30 60 0 1 2 10 20 3 6 7 8 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 10 20 30 60 ©Duane Szafron 1999 5 5 6 7 8

10 Merge Algorithm 3 l Copy the smallest from the two collections. 0 1 2 10 20 3 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 10 20 30 60 0 1 2 10 20 30 3 6 7 8 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 10 20 30 60 ©Duane Szafron 1999 5 5 6 7 8

11 Merge Algorithm 4 l Copy the smallest from the two collections. 0 1 2 10 20 30 3 4 5 6 7 8 40 50 70 80 90 0 1 2 3 4 10 20 30 60 5 6 7 8 0 1 2 3 4 5 6 7 8 10 20 30 40 40 50 70 80 90 0 1 2 3 4 10 20 30 60 ©Duane Szafron 1999 5 6 7 8

12 Merge Algorithm 5 l Copy the smallest from the two collections. 0 1 2 3 4 5 6 7 8 10 20 30 40 40 50 70 80 90 0 1 2 3 4 10 20 30 60 5 6 7 8 0 1 2 3 4 5 6 7 8 10 20 30 40 50 50 70 80 90 0 1 2 3 4 10 20 30 60 ©Duane Szafron 1999 5 6 7 8

13 Merge Algorithm 6 l Copy the smallest from the two collections. 0 1 2 3 4 5 6 7 8 10 20 30 40 50 50 70 80 90 0 1 2 3 4 10 20 30 60 5 6 7 8 0 1 2 3 4 3 6 7 8 10 20 30 40 50 60 70 80 90 0 1 2 3 4 10 20 30 60 ©Duane Szafron 1999 5 6 7 8

14 Merge Algorithm 7 l When one of the two collections is empty: – If the bottom collection is emptied first, then elements remain in the top collection, but they are in the correct place, so stop. 0 1 2 3 4 3 6 7 8 10 20 30 40 50 60 70 80 90 0 1 2 3 4 10 20 30 60 ©Duane Szafron 1999 5 6 7 8

15 Merge Algorithm 8 – If the top collection is emptied first, then elements remain in the bottom collection. – For example, if the original list had the 90 and 60 exchanged and the 80 and 30 exchanged, the top collection would be emptied first. 0 1 2 3 4 5 6 7 10 20 30 40 50 60 70 8 0 1 2 3 4 10 20 80 90 8 5 6 7 – All remaining elements must be copied from the bottom collection to the top. ©Duane Szafron 1999

Merge Algorithm - Arrays 1 private static void merge(Comparable top[ ], Comparable bottom[ ] int low, int middle, int high) { // pre: top[middle. . high] are ascending // bottom[low. . middle-1] are ascending // post: top[low. . high] are ascending int top. Index; //index of top array int bot. Index; //index of bottom array int result. Index; //index of result array top. Index = middle; bot. Index = low; result. Index = low; ©Duane Szafron 1999 code based on Bailey pg. 85 16

Merge Algorithm - Arrays 2 17 // as long as both collections are not empty while (bott. Index < middle) && (top. Index <= high) if (top[top. Index]. compare. To(bottom[bot. Index]) < 0) // copy from the top collection top[result. Index++] = top[top. Index++]; else // or copy from the bottom collection top[result. Index++] = bottom[bot. Index++]; What about remaining // copy any remaining elements from the bottom elements in top? for (bot. Index = bot. Index; bot. Index < middle; bot. Index++) top[result. Index++] = bottom[bot. Index++]; } ©Duane Szafron 1999 code based on Bailey pg. 85

Merge. Sort Algorithm l The Merge. Sort is recursive, so we create a wrapper method and the recursive method that it calls. ©Duane Szafron 1999 18

Merge. Sort Algorithm - Arrays public static void merge. Sort(Comparable an. Array[], int size) { // pre: 0 <= size <= an. Array. length // post: values in an. Array[0. . size - 1] are in // ascending order merge. Sort. R(an. Array, new int[size], 0, size - 1); } ©Duane Szafron 1999 code based on Bailey pg. 88 19

Merge. Sort. R Algorithm Arrays public static void merge. Sort. R(Comparable an. Array[ ], Comparable temp[ ], int low, int high) { // pre: 0 <= low <= high <= an. Array. length // post: values in an. Array[low. . high] are in ascending order int size; // size of the entire collection int index; // index for copying bottom into temp size = high - low + 1; if (size < 2) return; middle = (low + high) / 2; for (index = low; index < middle; index++) temp[index] = an. Array[index]; merge. Sort. R(temp, an. Array, low, middle - 1); merge. Sort. R(an. Array, temp, middle, high); merge(an. Array, temp, low, middle, high); } ©Duane Szafron 1999 code based on Bailey pg. 86 20

Merge. Sort Calling Sequence l m. SR(a, t, 0, 8) – m. SR(t, a, 0, 3) • m. SR(t, a, 0, 1) – ms. R(t, a, 0, 0) * – ms. R(a, t, 1, 1) * – merge(a, t, 0, 1, 1) • m. SR(a, t, 2, 3) – ms. R(t, a, 2, 2) * – ms. R(a, t, 3, 3) * – merge(a, t, 2, 3, 3) • merge(a, t, 0, 2, 3) * will not be traced ©Duane Szafron 1999 – m. SR(a, t, 4, 8) • m. SR(t, a, 4, 5) – m. SR(t, a, 4, 4) * – m. SR(a, t, 5, 5) * – merge(a, t, 4, 5, 5) • m. SR(a, t, 6, 8) – m. SR(t, a, 6, 6) * – m. SR(a, t, 7, 8) • m. SR(t, a, 7, 7) * • m. SR(a, t, 8, 8) * • merge(a, t, 7, 8, 8) – merge(a, t, 6, 7, 8) • merge(a, t, 4, 6, 8) – merge(a, t, 0, 4, 8) 21

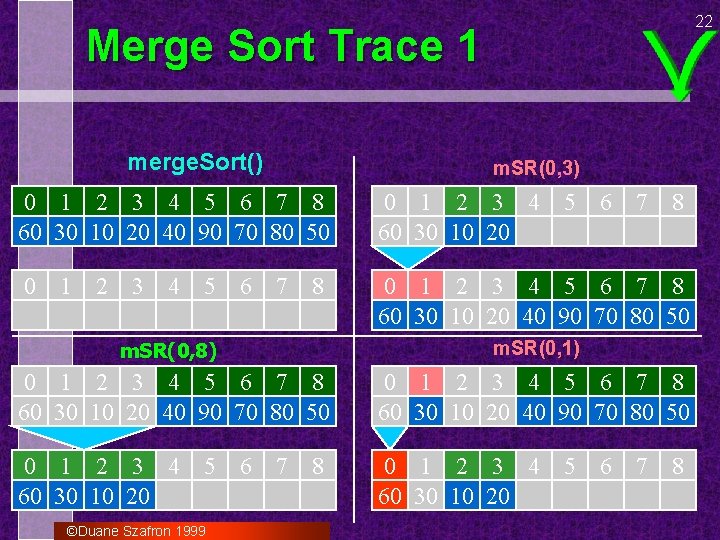
22 Merge Sort Trace 1 merge. Sort() m. SR(0, 3) 0 1 2 3 4 5 6 7 8 60 30 10 20 40 90 70 80 50 0 1 2 3 4 60 30 10 20 0 0 1 2 3 4 5 6 7 8 60 30 10 20 40 90 70 80 50 1 2 3 4 5 6 7 8 m. SR(0, 8) m. SR(0, 1) 0 1 2 3 4 5 6 7 8 60 30 10 20 40 90 70 80 50 0 1 2 3 4 60 30 10 20 5 ©Duane Szafron 1999 6 7 8 5 6 7 8

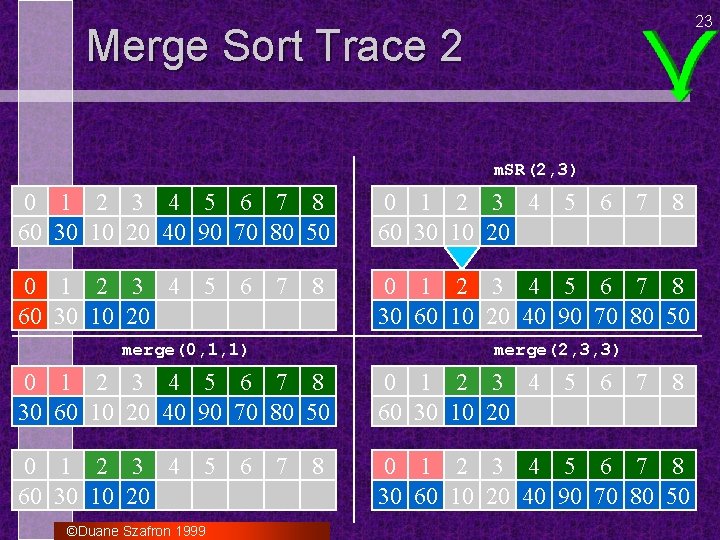
23 Merge Sort Trace 2 m. SR(2, 3) 0 1 2 3 4 5 6 7 8 60 30 10 20 40 90 70 80 50 0 1 2 3 4 60 30 10 20 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 5 6 7 8 merge(0, 1, 1) 5 6 7 8 merge(2, 3, 3) 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 0 1 2 3 4 60 30 10 20 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 5 ©Duane Szafron 1999 6 7 8 5 6 7 8

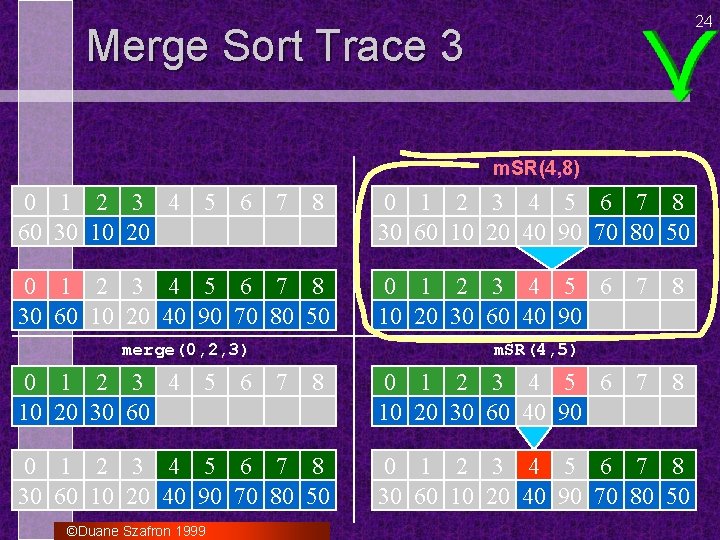
24 Merge Sort Trace 3 m. SR(4, 8) 0 1 2 3 4 60 30 10 20 5 6 7 8 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 merge(0, 2, 3) 0 1 2 3 4 10 20 30 60 5 6 0 1 2 3 4 5 6 10 20 30 60 40 90 7 8 m. SR(4, 5) 7 8 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 ©Duane Szafron 1999 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 0 1 2 3 4 5 6 10 20 30 60 40 90 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50

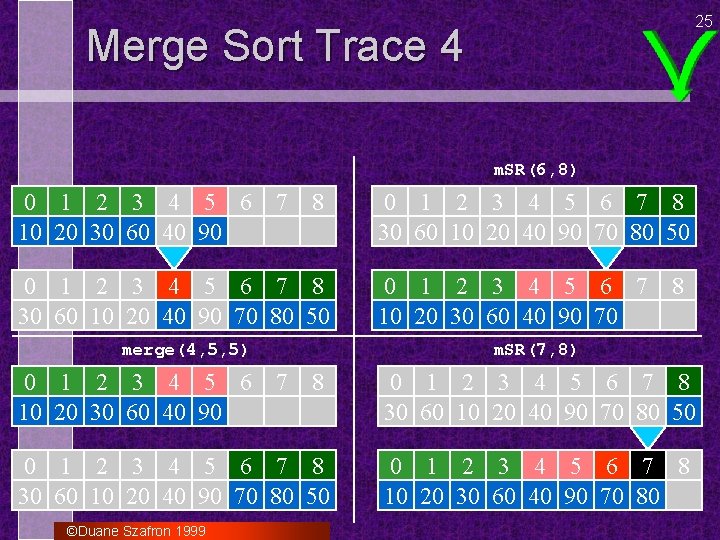
25 Merge Sort Trace 4 m. SR(6, 8) 0 1 2 3 4 5 6 10 20 30 60 40 90 7 8 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 merge(4, 5, 5) 0 1 2 3 4 5 6 10 20 30 60 40 90 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 0 1 2 3 4 5 6 7 10 20 30 60 40 90 70 8 m. SR(7, 8) 8 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 0 1 2 3 4 5 6 7 8 10 20 30 60 40 90 70 80 ©Duane Szafron 1999 7

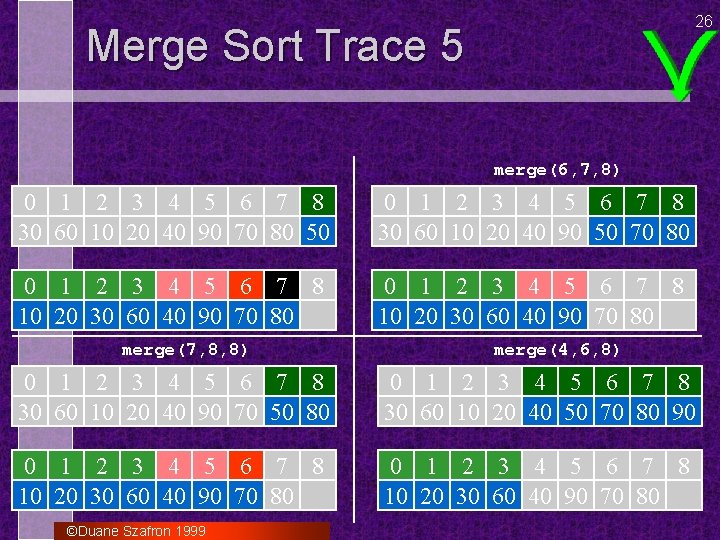
26 Merge Sort Trace 5 merge(6, 7, 8) 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 50 70 80 0 1 2 3 4 5 6 7 8 10 20 30 60 40 90 70 80 merge(7, 8, 8) merge(4, 6, 8) 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 50 80 0 1 2 3 4 5 6 7 8 30 60 10 20 40 50 70 80 90 0 1 2 3 4 5 6 7 8 10 20 30 60 40 90 70 80 ©Duane Szafron 1999

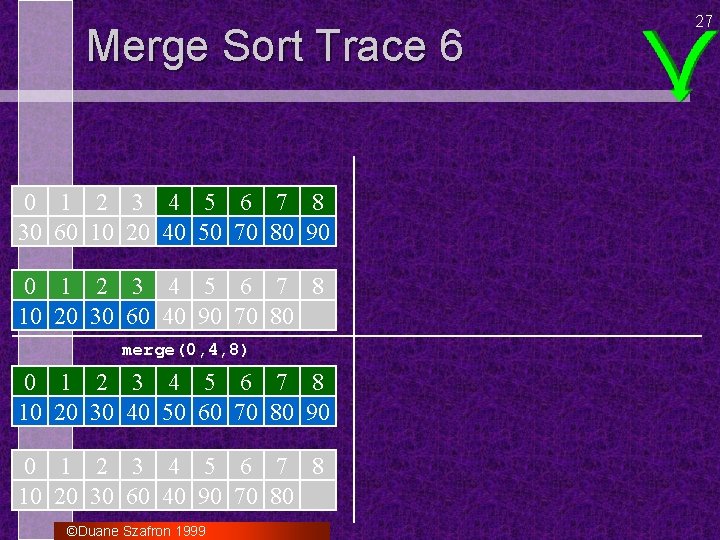
Merge Sort Trace 6 0 1 2 3 4 5 6 7 8 30 60 10 20 40 50 70 80 90 0 1 2 3 4 5 6 7 8 10 20 30 60 40 90 70 80 merge(0, 4, 8) 0 1 2 3 4 5 6 7 8 10 20 30 40 50 60 70 80 90 0 1 2 3 4 5 6 7 8 10 20 30 60 40 90 70 80 ©Duane Szafron 1999 27

28 Counting Comparisons 1 l How many comparison operations are required for a merge sort of an n-element collection? l The recursive sort method calls merge() once, each time it divides the collection in half. l Then there are n - 1 calls to merge: 1+2+4+8+. . . +2 i-1 where i = log n middle = (low + high) / 2; for (index = low; index < middle; index++) temp[index] = an. Array[index]; merge. Sort. R(temp, an. Array, low, middle - 1); merge. Sort. R(an. Array, temp, middle, high); merge(an. Array, temp, low, middle, high); ©Duane Szafron 1999 1 log n 2 i-1 = n-1

29 Counting Comparisons 2 Assume that the collection is always divided exactly in half. l Each time merge is executed for two lists of size k/2, it does comparisons in a loop and each time, either the bottom index or top index is incremented. l // as long as both collections are not empty while (bott. Index < middle) && (top. Index <= high) if (top[top. Index]. compare. To(bottom[bot. Index]) < 0) // copy from the top collection top[result. Index++] = top[top. Index++]; else // or copy from the bottom collection top[result. Index++] = bottom[bot. Index++]; ©Duane Szafron 1999

30 Comparisons - Best Case 1 In the best case, the same index (top or bottom) is incremented every time through the loop, so there are k/2 comparisons on each call to merge, for a call with two lists of size k/2. l Notice that each level has the same total number of comparisons: n/2 n=k=8 4 k=4 best case 2 2 comparisons k=2 k=2 per merge l 1 1 k=1 k=1 ©Duane Szafron 1999 1 1 k=1 k=1

31 Comparisons - Best Case 2 l Since the depth of the tree is log(n), the total number of comparisons is: n/2 * log(n) = O(n log(n)) ©Duane Szafron 1999

32 Comparisons - Worst Case 1 l In the worst case, the index that is incremented alternates each time through the loop, so there are k comparisons on each call to merge, for a call with two lists of size k/2. n=k=8 8 worst case comparisons per merge ©Duane Szafron 1999 k=4 4 k=2 2 2 k=1 k=1

33 Comparisons - Worst Case 2 l Since the depth of the tree is log(n), the total number of comparisons is: n * log(n) = O(n log(n)) ©Duane Szafron 1999

34 Comparisons - Average Case l The average case must be between the best case and the worst case so the average case is: O(n log(n)) ©Duane Szafron 1999

35 Counting Assignments 1 How many assignment operations are required for a merge sort of an n-element collection? l In the merge method, there is one assignment for every comparison: l // as long as both collections are not empty while (bott. Index < middle) && (top. Index <= high) if (top[top. Index]. compare. To(bottom[bot. Index]) < 0) // copy from the top collection top[result. Index++] = top[top. Index++]; else // or copy from the bottom collection top[result. Index++] = bottom[bot. Index++]; ©Duane Szafron 1999

36 Counting Assignments 2 l However, the recursive sort method “copies” half of a collection of size k to the other collection which takes an extra k/2 assignments for each merge: middle = (low + high) / 2; for (index = low; index < middle; index++) temp[index] = an. Array[index]; merge. Sort. R(temp, an. Array, low, middle - 1); merge. Sort. R(an. Array, temp, middle, high); merge(an. Array, temp, low, middle, high); ©Duane Szafron 1999

37 Counting Assignments 3 l In addition, during a merge, any remaining elements on the bottom (but not the top), must be copied: // copy any remaining elements from the bottom for (bot. Index = bot. Index; bot. Index < middle; bot. Index++) top[result. Index++] = bottom[bot. Index++]; ©Duane Szafron 1999

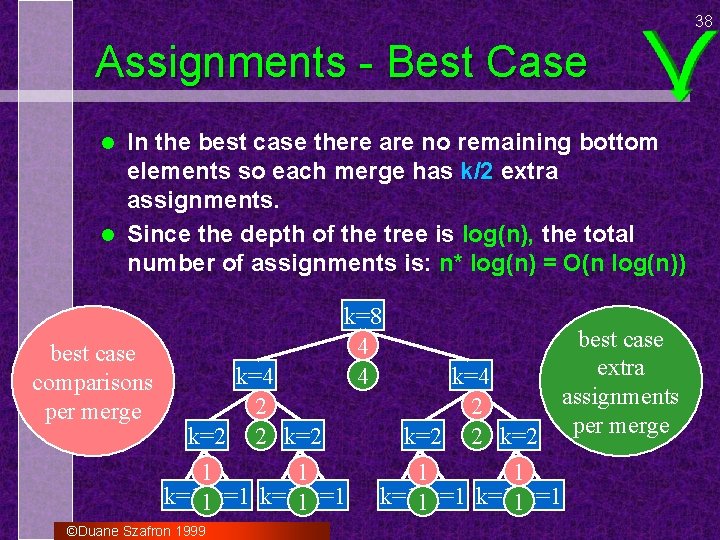
38 Assignments - Best Case In the best case there are no remaining bottom elements so each merge has k/2 extra assignments. l Since the depth of the tree is log(n), the total number of assignments is: n* log(n) = O(n log(n)) l best case comparisons per merge k=8 4 4 k=4 2 k=2 1 1 k=11 k=1 ©Duane Szafron 1999 k=4 2 k=2 1 1 k=11 k=1 best case extra assignments per merge

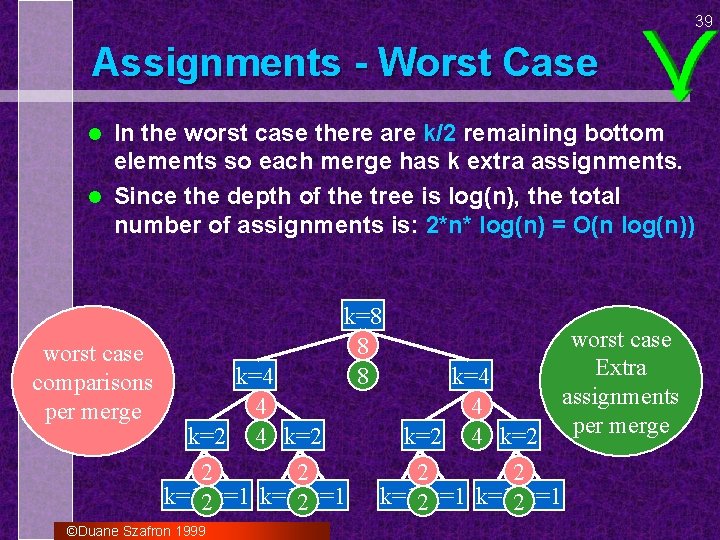
39 Assignments - Worst Case In the worst case there are k/2 remaining bottom elements so each merge has k extra assignments. l Since the depth of the tree is log(n), the total number of assignments is: 2*n* log(n) = O(n log(n)) l worst case comparisons per merge k=8 8 8 k=4 4 k=2 2 2 k=12 k=1 ©Duane Szafron 1999 k=4 4 k=2 2 2 k=12 k=1 worst case Extra assignments per merge

40 Assignments - Average Case l The average case is between the best and worst case so the average number of assignments must also be: O(n log(n)). ©Duane Szafron 1999

41 Time Complexity of Merge Sort l Best case: O(n log(n)) for comparisons and assignments. l Worst case O(n log(n)) for comparisons and assignments. l Average case O(n log(n)) for comparisons and assignments. l Note that the insertion sort is actually a better sort than the merge sort if the original collection is almost sorted. ©Duane Szafron 1999

42 Space Complexity of Merge Sort l Besides the collection itself, an extra collection of references of the same size is needed. l Therefore, the space complexity of Merge Sort is still O(n), but doubling the collection storage may sometimes be a problem. l Does the recursion require extra space and if so, how much? ©Duane Szafron 1999