Revised 12600 Sorting Insertion Sort Cmput 115 Lecture

Revised 1/26/00 Sorting - Insertion Sort Cmput 115 - Lecture 11 Department of Computing Science University of Alberta ©Duane Szafron 2000 Some code in this lecture is based ©Duane Szafron 1999 on code from the book: Java Structures by Duane A. Bailey or the companion structure package

2 About This Lecture l In this lecture we will learn about a sorting algorithm called the Insertion Sort. l We will study its implementation and its time and space complexity. ©Duane Szafron 1999

3 Outline The Insertion Sort Algorithm l Insertion Sort - Arrays l Time and Space Complexity of Insertion Sort l ©Duane Szafron 1999

4 The Sort Problem l Given a collection, with elements that can be compared, put the elements in increasing or decreasing order. 0 1 2 3 4 5 6 7 8 60 30 10 20 40 90 70 80 50 0 1 2 3 4 5 6 7 8 10 20 30 40 50 60 70 80 90 ©Duane Szafron 1999

5 Insertion Sort Algorithm 1 l The lower part of the collection is sorted and the higher part is unsorted. 0 1 2 3 4 5 6 7 8 60 30 10 20 40 90 70 80 50 l Insert the first element of the unsorted part into the correct place in the sorted part. 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 ©Duane Szafron 1999

6 Insertion Sort Algorithm 2 0 1 2 3 4 5 6 7 8 30 60 10 20 40 90 70 80 50 0 1 2 3 4 5 6 7 8 10 30 60 20 40 90 70 80 50 0 1 2 3 4 5 6 7 8 10 20 30 60 40 90 70 80 50 ©Duane Szafron 1999

7 Insertion Sort Algorithm 3 0 1 2 3 4 5 6 7 8 10 20 30 60 40 90 70 80 50 0 1 2 3 4 5 6 7 8 10 20 30 40 60 90 70 80 50 ©Duane Szafron 1999

8 Insertion Sort Algorithm 4 0 1 2 3 4 5 6 7 8 10 20 30 40 60 90 70 80 50 0 1 2 3 4 5 6 7 8 10 20 30 40 60 70 90 80 50 0 1 2 3 4 5 6 7 8 10 20 30 40 60 70 80 90 50 0 1 2 3 4 5 6 7 8 10 20 30 40 50 60 70 80 90 ©Duane Szafron 1999

9 Insertion Sort Code - Arrays public static void insertion. Sort(Comparable an. Array[], int size) { // pre: 0 <= size <= an. Array. length // post: values in an. Array are in ascending order int index; //index of start of unsorted part } for (index = 1; index < size; index++) { this. move. Element. At(an. Array, index); } ©Duane Szafron 1999 code based on Bailey pg. 83

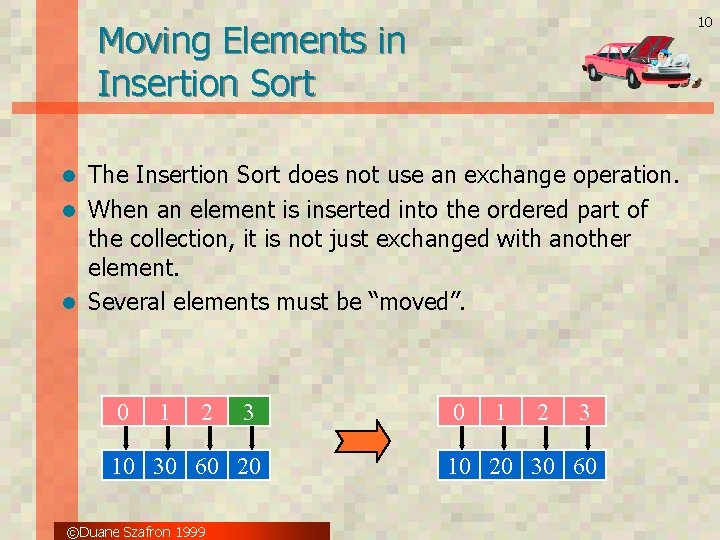
10 Moving Elements in Insertion Sort The Insertion Sort does not use an exchange operation. l When an element is inserted into the ordered part of the collection, it is not just exchanged with another element. l Several elements must be “moved”. l 0 1 2 3 10 30 60 20 ©Duane Szafron 1999 0 1 2 3 10 20 30 60

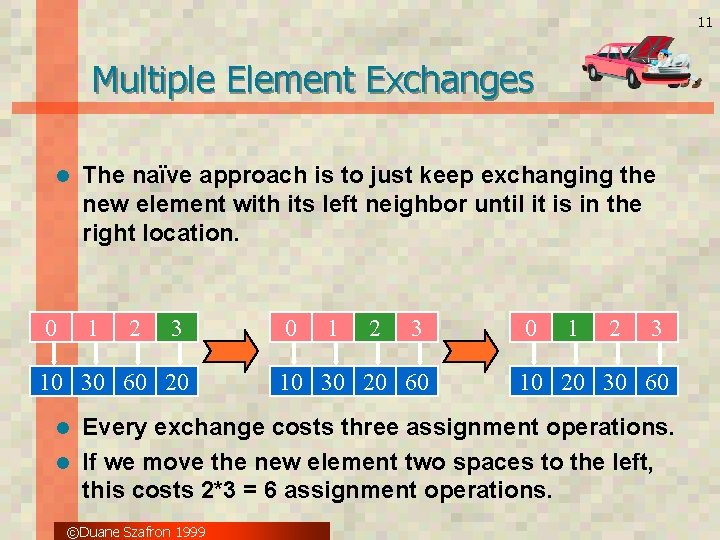
11 Multiple Element Exchanges l 0 The naïve approach is to just keep exchanging the new element with its left neighbor until it is in the right location. 1 2 3 10 30 60 20 0 1 2 3 10 30 20 60 0 1 2 3 10 20 30 60 Every exchange costs three assignment operations. l If we move the new element two spaces to the left, this costs 2*3 = 6 assignment operations. l ©Duane Szafron 1999

Method - move. Element. At() - Arrays 12 public static void move. Element. At(Comparable an. Array[ ], int last) { // pre: 0 <= last < an. Array. length and an. Array in // ascending order from 0 to last-1 // post: an. Array in ascending order from 0 to last int temp; //A reference to the element being moved while ((last>0) && (temp. compare. To. an. Array[last-1]) < 0) { this. swap(an. Array, last - 1); last--; } } ©Duane Szafron 1999 INEFFICIENT code based on Bailey pg. 83

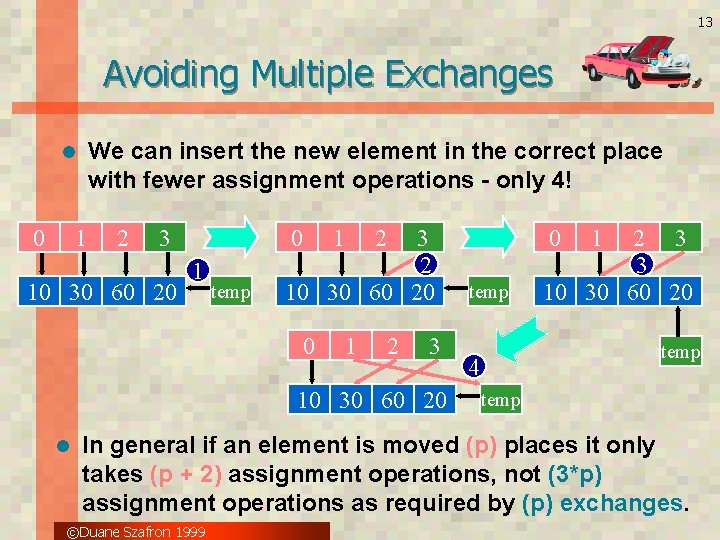
13 Avoiding Multiple Exchanges We can insert the new element in the correct place with fewer assignment operations - only 4! l 0 1 2 3 10 30 60 20 0 1 temp 3 2 10 30 60 20 0 1 2 3 10 30 60 20 l 0 temp 1 2 3 3 10 30 60 20 temp 4 temp In general if an element is moved (p) places it only takes (p + 2) assignment operations, not (3*p) assignment operations as required by (p) exchanges. ©Duane Szafron 1999

Recall Element Insertion in a Vector This operation is similar to inserting a new element in a Vector. l Each existing element was “moved” to the right before inserting the new element in its correct location. l ©Duane Szafron 1999 14

15 Recall Vector Insertion Code public void insert. Element. At(Object object, int index) { //pre: 0 <= index <= size() //post: inserts the given object at the given index, // moving elements from index to size()-1 to the right int i; this. ensure. Capacity(this. element. Count + 1); for (i = this. element. Count; i > index; i--) this. element. Data[i] = this. element. Data[i - 1]; this. element. Data[index] = object; this. element. Count++; } ©Duane Szafron 1999 code based on Bailey pg. 39

Differences from Element Insertion l In Vector element insertion: – We have a reference to the new element. – We know the index location for the new element. l In the Insertion sort: – We don’t have a reference to the new element, only an index in the array where the new element is currently located. – We don’t know the index location for the new element. We need to find the index by comparing the new element with the elements in the collection from left to right. ©Duane Szafron 1999 16

Method - move. Element. At() - Arrays public static void move. Element. At(Comparable an. Array[], int last) { // pre: 0 <= last < an. Array. length and an. Array in // ascending order from 0 to last-1. // post: an. Array in ascending order from 0 to last // int move; //A reference to the element being moved move = an. Array[last]; while ((last>0) && (move. compare. To. an. Array[last-1]) < 0) { an. Array[last] = an. Array[last - 1]; last--; } an. Array[last] = move; } code based on Bailey pg. 83 ©Duane Szafron 1999 17

18 Counting Comparisons How many comparison operations are required for an insertion sort of an n-element collection? l The sort method calls move. Element. At() in a loop for the indexes: i = 1, 2, … n - 1. for (index = 1; index < size; index++) { this. move. Element. At(an. Array, index); l l Each time move. Element. At() is executed for some argument, last, it does a comparison in a loop for some of the indexes: k, k-1, … 1. while ((last>0) && (temp. compare. To. an. Array[last-1]) < 0) { an. Array[last] = an. Array[last - 1]; last--; } ©Duane Szafron 1999

19 Comparisons - Best Case l In the best case there is 1 comparison per call since the first comparison terminates the loop. while ((last>0) && (temp. compare. To. an. Array[last-1]) < 0) { an. Array[last] = an. Array[last - 1]; last--; } move(a, 1) 1 l move(a, 2) . . . 1 The total number of comparisons is: (n - 1) * 1 = n - 1 = O(n) ©Duane Szafron 1999 move(a, n-1) 1

20 Comparisons - Worst Case l In the worst case there are k comparisons per call since the loop is not terminated until k == 0. while ((last>0) && (temp. compare. To. an. Array[last-1]) < 0) { an. Array[last] = an. Array[last - 1]; last--; } move(a, 1) 1 l move(a, 2) . . . 2 The total number of comparisons is: 1 + 2 + … (n - 1) = [(n-1)*n] / 2 = O(n 2) ©Duane Szafron 1999 move(a, n-1) n-1

21 Comparisons - Average Case 1 l In the average case it is equally probable that the number of comparisons is any number between 1 and k inclusive for each call. while ((last>0) && (temp. compare. To. an. Array[last-1]) < 0) { an. Array[last] = an. Array[last - 1]; last--; } move(a, 1) move(a, 2) move(a, n-1). . . 1 l 1 2 1 Note that the average for each call is: (1 + 2 + … k)/k = [k*(k+1)]/[2*k] = (k+1)/2 ©Duane Szafron 1999 2. . . n-1

22 Comparisons - Average Case 2 l In the average case, the total number of comparisons is: (1+1)/2 + (2+1)/2 + … + ((n-1) + 1)/2 = 1/2 + 2/2 + 1/2 + … + (n-1)/2 + 1/2 = [1 + 2 + … + (n-1)]*(1/2) + (n-1)*(1/2) = [ (n-1)*n/2]*(1/2) + (n-1)*(1/2) = [ (n-1)*n]*(1/4) + 2*(n-1)*(1/4) = [ (n-1)*n + 2*(n-1)]*(1/4) = [ (n-1)*(n + 2)]*(1/4) = O(n 2) ©Duane Szafron 1999

23 Counting Assignments 1 How many assignment operations are required for an insertion sort of an n-element collection? l The sort method calls move. Element. At() in a loop for the indexes: k = 1, 2, … n - 1. l Every time the method is called, the element is moved one place for each successful comparison. l It requires p+2 assignment operations to move the new element p places. l ©Duane Szafron 1999

24 Assignments - Best Case l In the best case there is 1 comparison per call and it fails. This means there are 0 successful comparisons, so there are 0+2 = 2 assignments per call. l In the best case there is a total number of assignments: 2 *(n-1) = O(n). When will this happen? ©Duane Szafron 1999

25 Exchanges - Worst Case l In the worst case there are k comparisons per call and they all succeed. This results in k+2 assignments per call. l In the worst case there is a total number of assignments: (1+2) + (2+2) + … + (n-1+2) = 3 + 4 + … + n+1 = [(n+1)*(n+2) - 3]/2 = O(n 2) ©Duane Szafron 1999

26 Assignments - Average l We have already seen that the average number of comparisons when inserting an element into a list of size k is: (k+1)/2 l On average, half of the time, the last comparison succeeds and half of the time it fails so the average number of successful comparisons is: (k+1)/2 - (1/2) = (k/2) l Therefore, the average number of total assignments is: 1/2 + 2/2 + … + (n-1)/2 = [1 + 2 + … + (n-1)]*(1/2) [ (n-1)*n/2]*(1/2) = (n-1)*n/4 = O(n 2) ©Duane Szafron 1999

Time Complexity of Insertion Sort Best case O(n) for comparisons and assignments. l Worst case O(n 2) for comparisons and assignments. l Average case O(n 2) for comparisons and assignments. l l Note: this means that for nearly sorted collections, collections insertion sort is better than selection sort even though in average and worst cases, they are the same: O(n 2). ©Duane Szafron 1999 27

Space Complexity of Insertion Sort l Besides the collection itself, the only extra storage for this sort is the single temp reference used in the move element method. l Therefore, the space complexity of Insertion Sort is O(n). ©Duane Szafron 1999 28