Review What is a Monomial An expression with

Review What is a Monomial? An expression with only one term. E. g 3 x 2 What is a Binomial? An expression with two unlike terms. E. g 5 x - 1 What is a trinomial? An expression with three unlike terms. E. g x+ 3 y 2 - 2 What is a quadratic equation? An expression in the form ax 2+bx+c, where a≠ 0. If you were to graph y=x+3, what would it look like? A straight line with a slope of one and a y-intercept of 3. 1

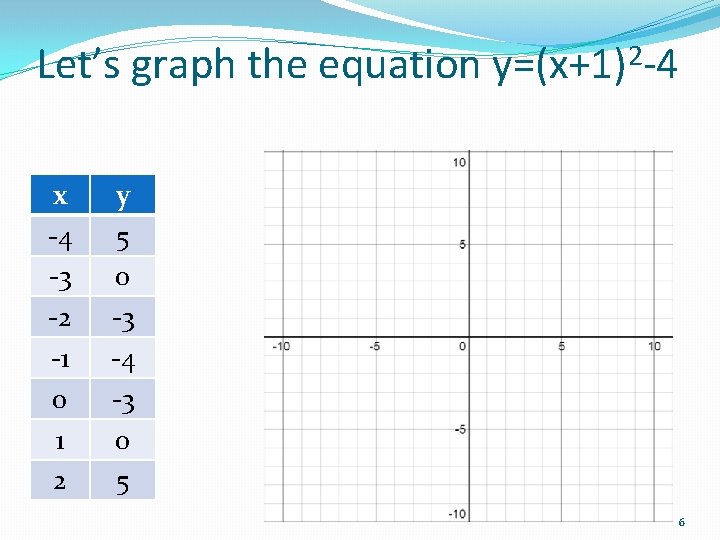
If y=(x+1)2 -4, complete the table below: x -4 -3 -2 -1 0 1 2 y=(x+1)2 -4 (-4+1)2 -4=(-3) 2 -4=9 -4=5 0 (-2+1) 2 -4=1 -4=-3 -4 (0+1) 2 -4=1 -4=-3 (1+1) 2 -4=4 -4=0 5 2

Questions for thought What does a quadratic equation look like if we graphed it? What kind of properties does a quadratic equation have? What are the differences between a quadratic equation and a linear equation? 3

Unit - Quadratics Relations 1 Topic: Modeling with Quadratic Relations 4

Key Definitions Quadratic relation – an algebraic expression that contains an x 2 and no other terms with exponents greater than 2. Quadratic Equation - An expression in the form y=ax 2+bx+c, where a≠ 0. Parabola – the graph of a quadratic relation. 5

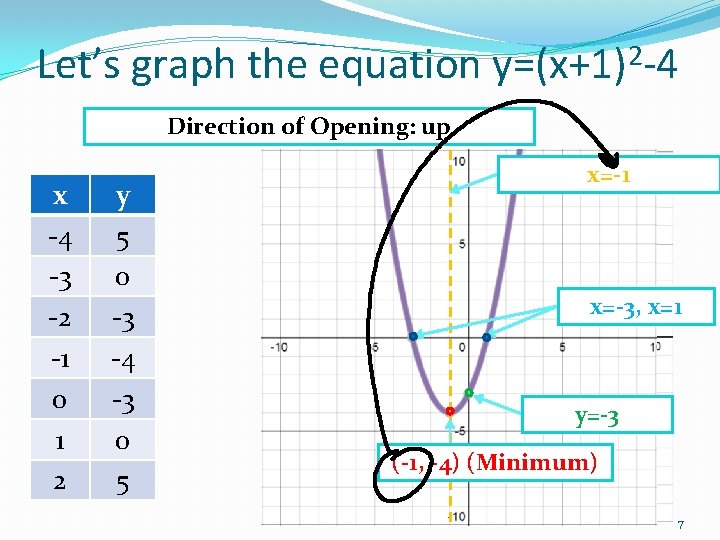
Let’s graph the equation y=(x+1)2 -4 x -4 -3 -2 -1 0 1 2 y 5 0 -3 -4 -3 0 5 6

Let’s graph the equation y=(x+1)2 -4 Direction of Opening: up x -4 -3 -2 -1 0 1 2 y 5 0 -3 -4 -3 0 5 Axis ofx=-1 Symmetry x-intercepts x=-3, x=1 y-intercept y=-3 Vertex (-1, -4) (Minimum) 7

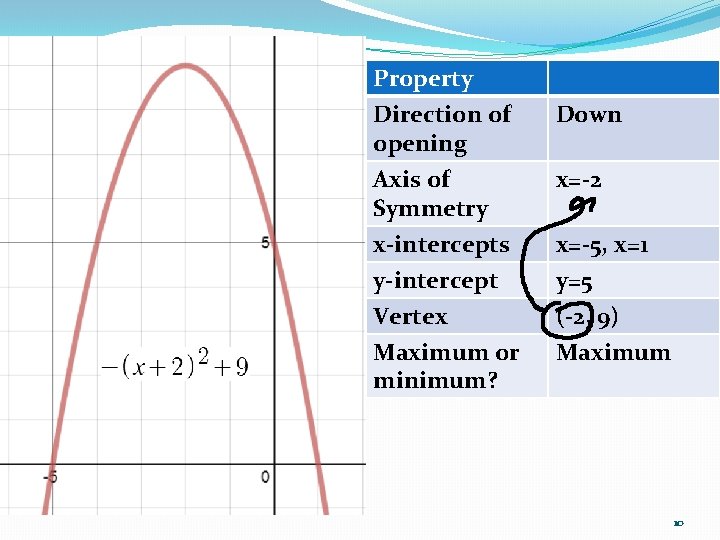
Parabola Properties Axis of Symmetry – The line which divides the parabola into two mirrored branches (one side reflects the other) x-intercepts / zeros / roots – Where the parabola crosses the x-axis y-intercept – Where the graph crosses the y-axis. 8

Parabola Characteristics Direction of opening / concavity – Direction in which the parabola opens. “If it opens down, it’s a frown”. ” If it opens up, it’s a smile. ” Vertex / Turning point – Where the parabola changes direction. Either a minimum or maximum depending on the direction of opening. Maximum if it opens down and minimum if it opens up. 9

Property Direction of opening Axis of Symmetry Down x=-2 x-intercepts x=-5, x=1 y-intercept Vertex Maximum or minimum? y=5 (-2, 9) Maximum 10

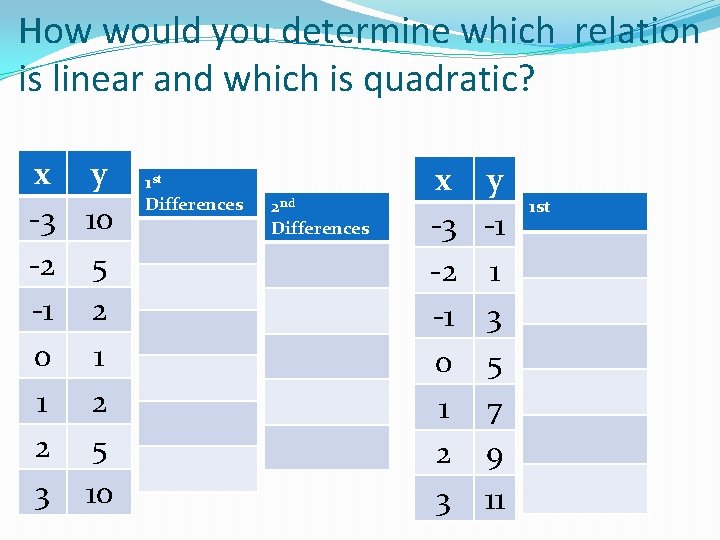
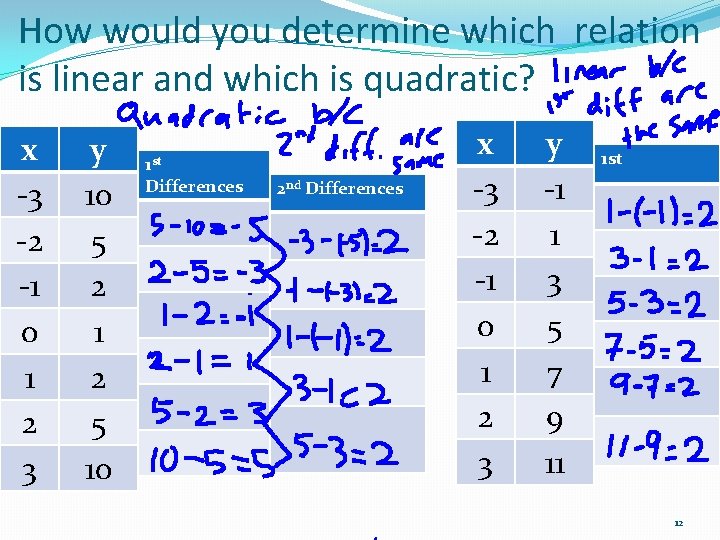
How would you determine which relation is linear and which is quadratic? x y -3 10 -2 5 -1 2 0 1 1 2 2 5 3 10 1 st Differences 2 nd Differences x -3 -2 -1 0 1 2 3 y -1 1 3 5 7 9 11 1 st

How would you determine which relation is linear and which is quadratic? x -3 -2 -1 0 1 2 3 y 10 5 2 1 2 5 10 1 st Differences 2 nd Differences x -3 -2 -1 0 1 2 3 y -1 1 3 5 7 9 11 1 st 12

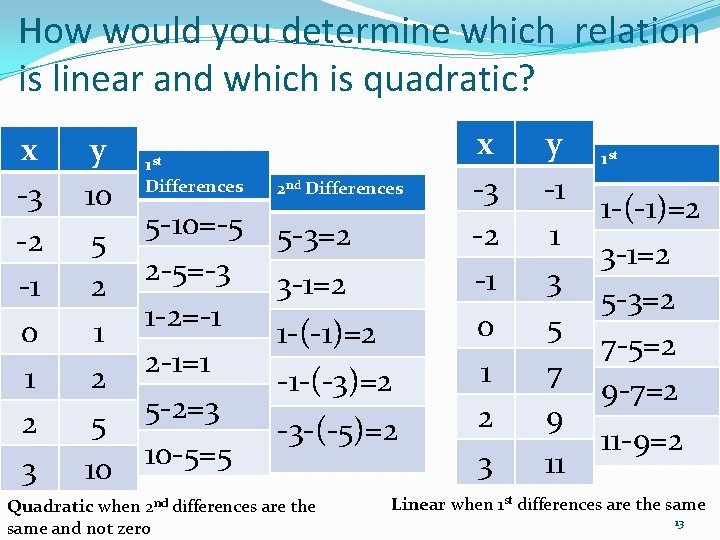
How would you determine which relation is linear and which is quadratic? x -3 -2 -1 0 1 2 3 y 10 5 2 1 2 5 10 1 st Differences 5 -10=-5 2 -5=-3 1 -2=-1 2 -1=1 5 -2=3 10 -5=5 2 nd Differences 5 -3=2 3 -1=2 1 -(-1)=2 -1 -(-3)=2 -3 -(-5)=2 Quadratic when 2 nd differences are the same and not zero x -3 -2 -1 0 1 2 3 y -1 1 3 5 7 9 11 1 st 1 -(-1)=2 3 -1=2 5 -3=2 7 -5=2 9 -7=2 11 -9=2 Linear when 1 st differences are the same 13

Identify the following as either linear, quadratic or neither: y = 3 x _____________ y = 4 x 3 _____________ y = 2 x 2 _____________ y = -3 x 2 – 1 _____________ y = 6 x + 8 _____________ y = 2(x + 4)2 _____________ y = (x – 3)2 – 9 _____________ y = 5(x – 2)2 + 11 _____________ 14

Identify the following as either linear, quadratic or neither: y = 3 x Linear y = 4 x 3 Neither y = 2 x 2 Quadratic y = -3 x 2 – 1 Quadratic y = 6 x + 8 Linear y = 2(x + 4)2 Quadratic y = (x – 3)2 – 9 Quadratic y = 5(x – 2)2 + 11 Quadratic 15