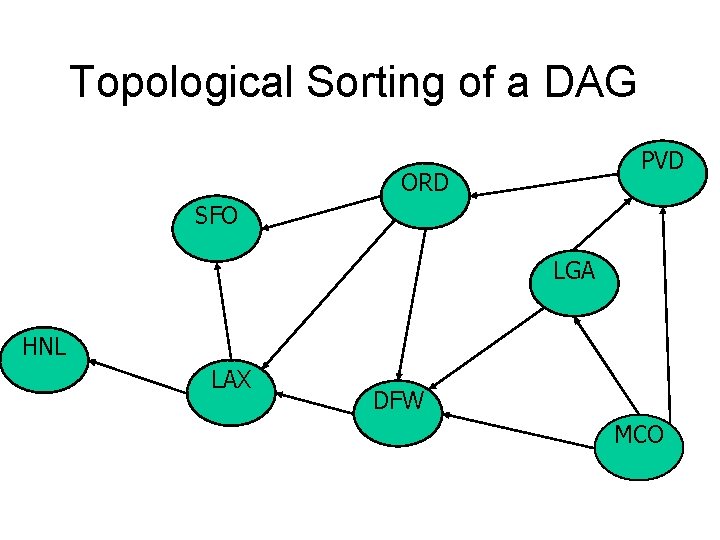
Review Topological Sorting of a DAG PVD ORD








- Slides: 56

Review

Topological Sorting of a DAG PVD ORD SFO LGA HNL LAX DFW MCO

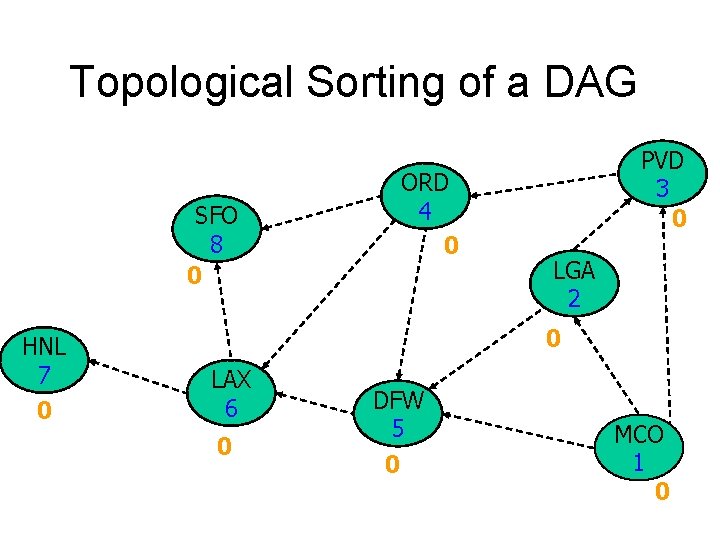
Topological Sorting of a DAG ORD 4 0 SFO 8 0 HNL 7 0 PVD 3 0 LGA 2 0 LAX 6 0 DFW 5 0 MCO 1 0

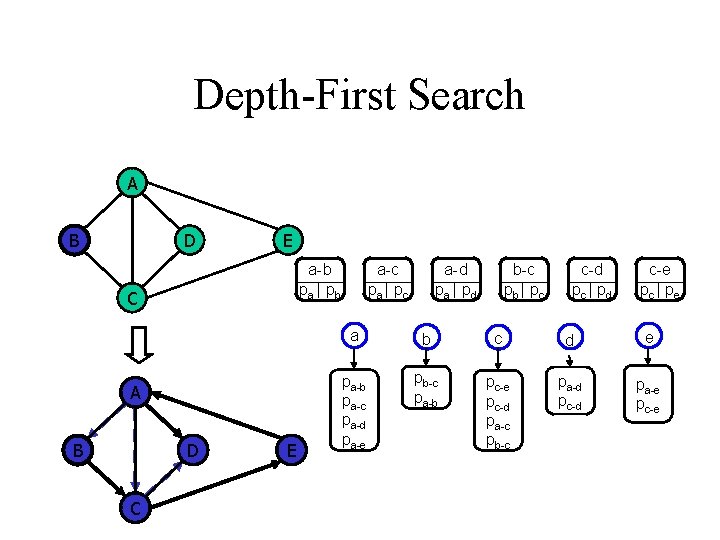
Depth-First Search A B D E a-b pa | pb C A B D C E a-c pa | p c a-d pa | p d b-c pb | p c c-d pc | p d c-e pc | pe a b c d e pa-b pa-c pa-d pa-e pb-c pa-b pc-e pc-d pa-c pb-c pa-d pc-d pa-e pc-e

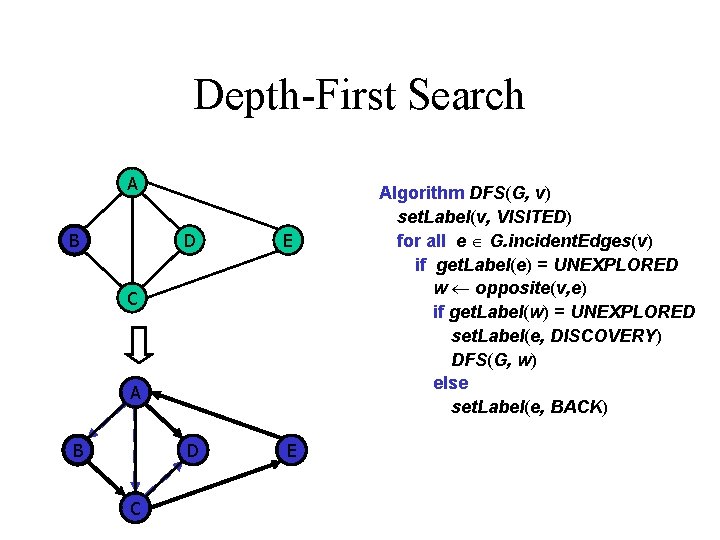
Depth-First Search A B D E C A B C Algorithm DFS(G, v) set. Label(v, VISITED) for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) DFS(G, w) else set. Label(e, BACK)

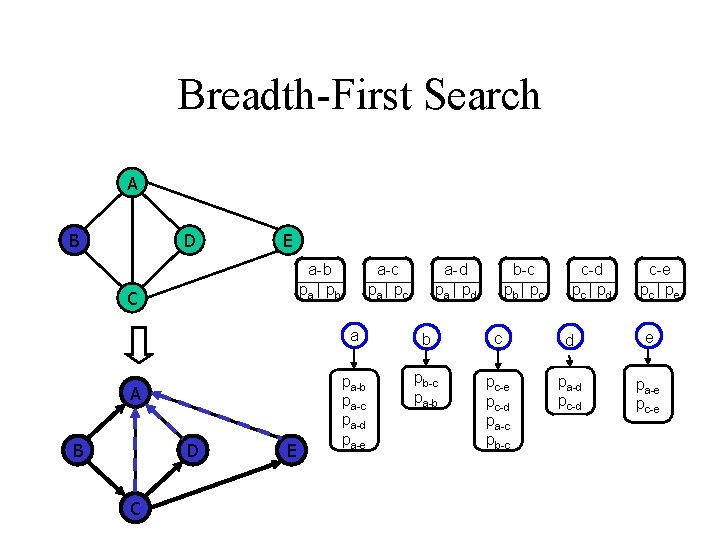
Breadth-First Search A B D E a-b pa | pb C A B D C E a-c pa | p c a-d pa | p d b-c pb | p c c-d pc | p d c-e pc | pe a b c d e pa-b pa-c pa-d pa-e pb-c pa-b pc-e pc-d pa-c pb-c pa-d pc-d pa-e pc-e

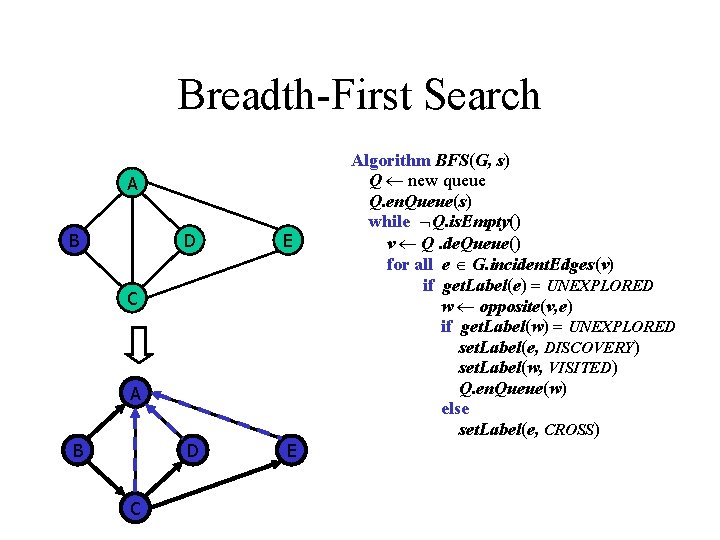
Breadth-First Search A B D E C A B C Algorithm BFS(G, s) Q new queue Q. en. Queue(s) while Q. is. Empty() v Q. de. Queue() for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) set. Label(w, VISITED) Q. en. Queue(w) else set. Label(e, CROSS)

Shortest Paths

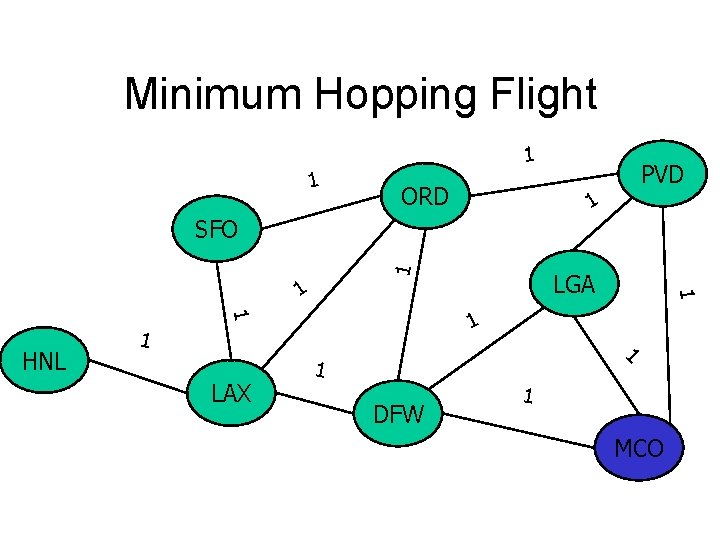
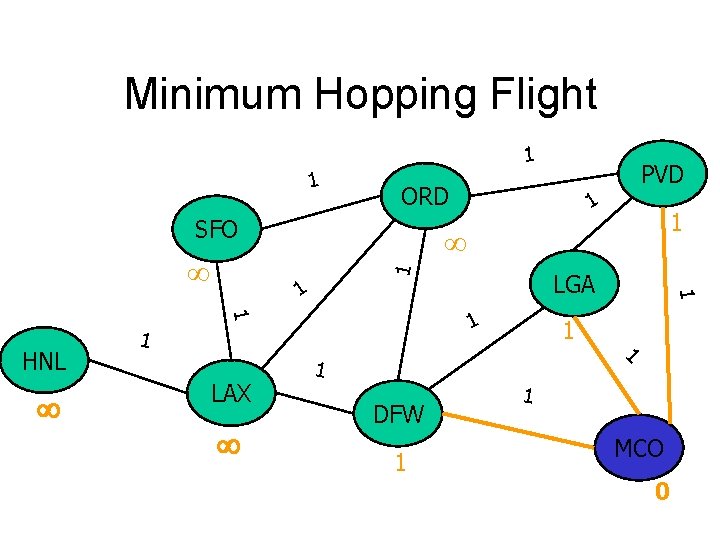
Minimum Hopping Flight 1 1 ORD PVD 1 1 SFO 1 1 HNL 1 LAX LGA 1 1 DFW 1 MCO

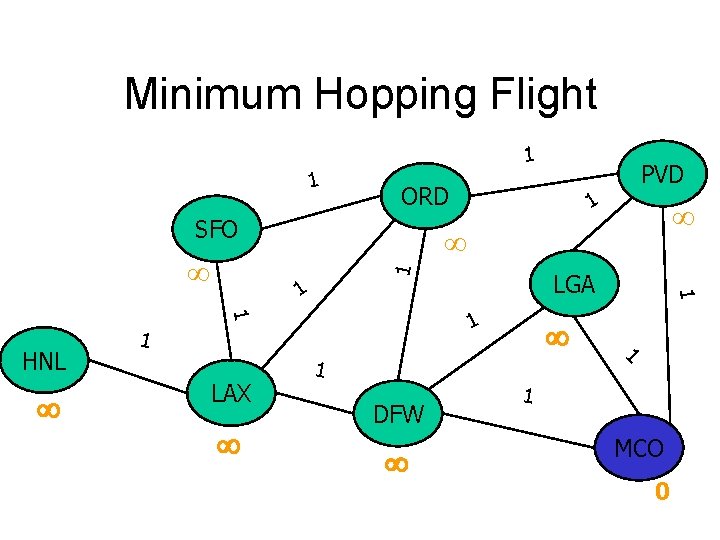
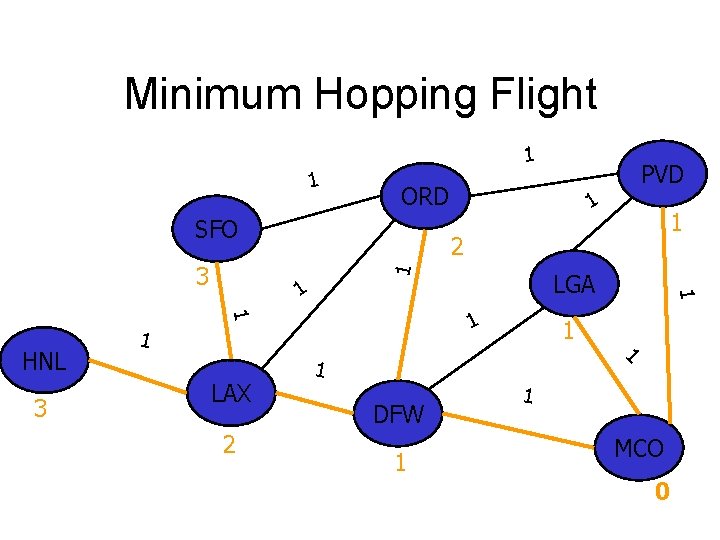
Minimum Hopping Flight 1 1 ORD SFO 1 1 LGA 1 1 LAX 1 HNL 1 1 DFW 1 PVD 1 1 MCO 0

Minimum Hopping Flight 1 1 ORD SFO 1 1 LGA 1 1 LAX 1 1 HNL 1 1 1 DFW 1 1 PVD 1 1 MCO 0

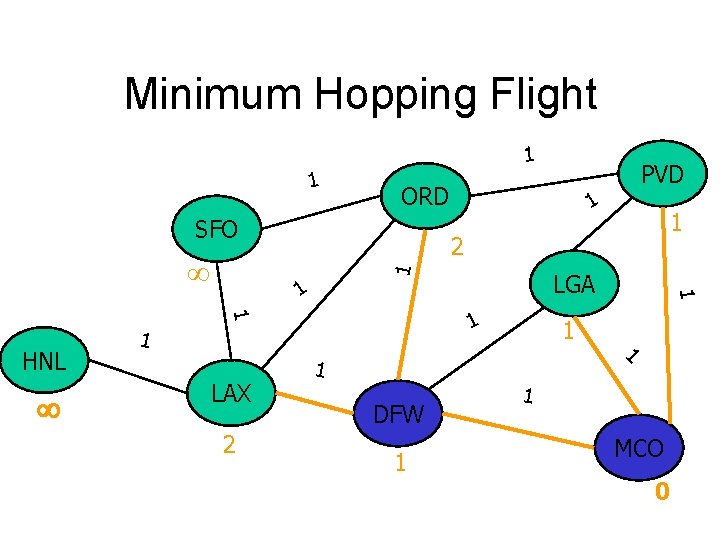
Minimum Hopping Flight 1 1 ORD SFO 1 1 2 LGA 1 1 LAX 1 2 1 HNL 1 1 1 DFW 1 1 PVD 1 1 MCO 0

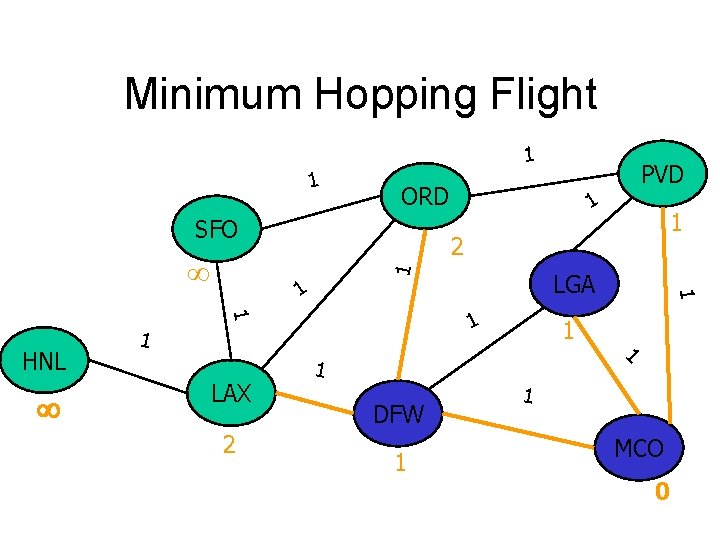
Minimum Hopping Flight 1 1 ORD SFO 1 1 2 LGA 1 1 LAX 1 2 1 HNL 1 1 1 DFW 1 1 PVD 1 1 MCO 0

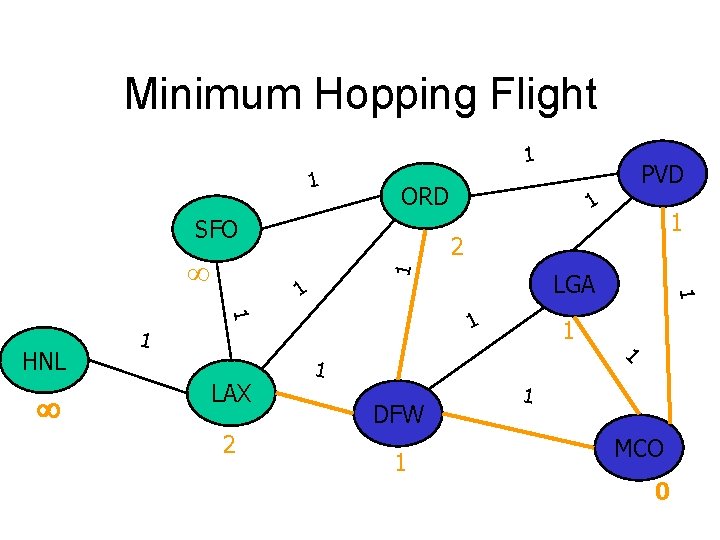
Minimum Hopping Flight 1 1 ORD SFO 1 1 2 LGA 1 1 LAX 1 2 1 HNL 1 1 1 DFW 1 1 PVD 1 1 MCO 0

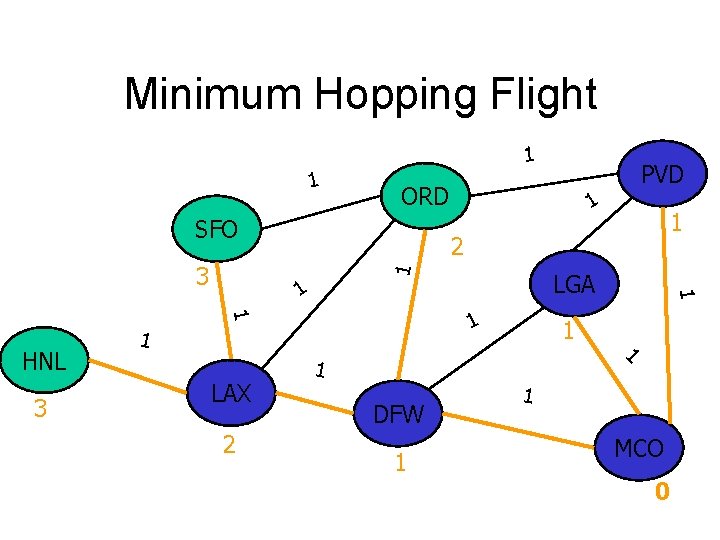
Minimum Hopping Flight 1 1 ORD SFO 1 1 3 2 LGA 1 1 LAX 1 2 1 HNL 1 1 1 DFW 1 1 3 PVD 1 1 MCO 0

Minimum Hopping Flight 1 1 ORD SFO 1 1 3 2 LGA 1 1 LAX 1 2 1 HNL 1 1 1 DFW 1 1 3 PVD 1 1 MCO 0

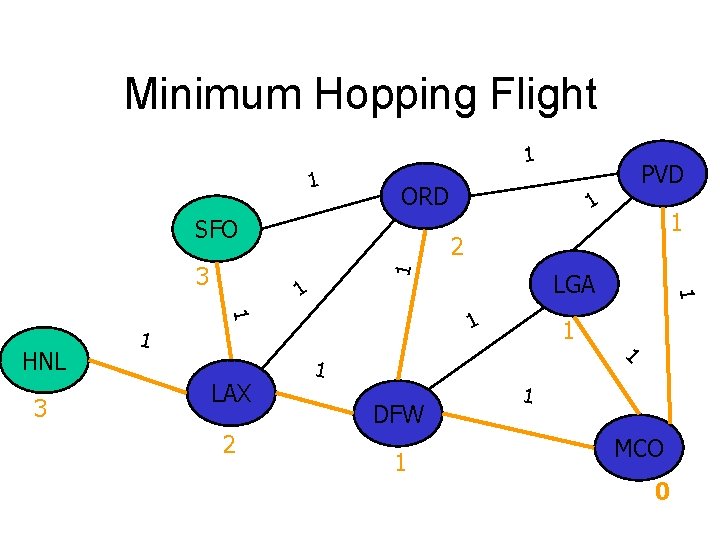
Minimum Hopping Flight 1 1 ORD SFO 1 1 3 2 LGA 1 1 LAX 1 2 1 HNL 1 1 1 DFW 1 1 3 PVD 1 1 MCO 0

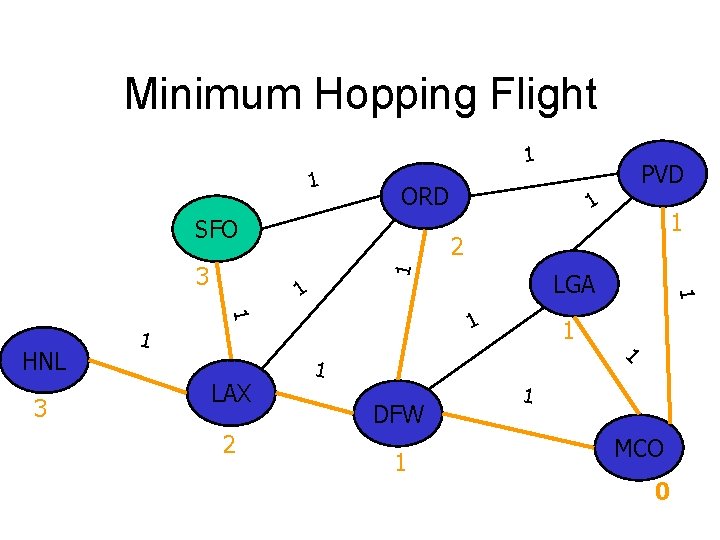
Minimum Hopping Flight 1 1 ORD SFO 1 1 3 2 LGA 1 1 LAX 1 2 1 HNL 1 1 1 DFW 1 1 3 PVD 1 1 MCO 0

Shortest Path when each edge is equally important Algorithm Shortest. Path (G, s) for all v G. vertices() if v = s s. distance 0 else s. distance v. parent null Q new queue Q. en. Queue(s) while Q. is. Empty() v Q. de. Queue() for all e G. incident. Edges(v) w opposite(v, e) if w. distance = w. distance v. distance + 1 w. parent v Q. en. Queue(v)

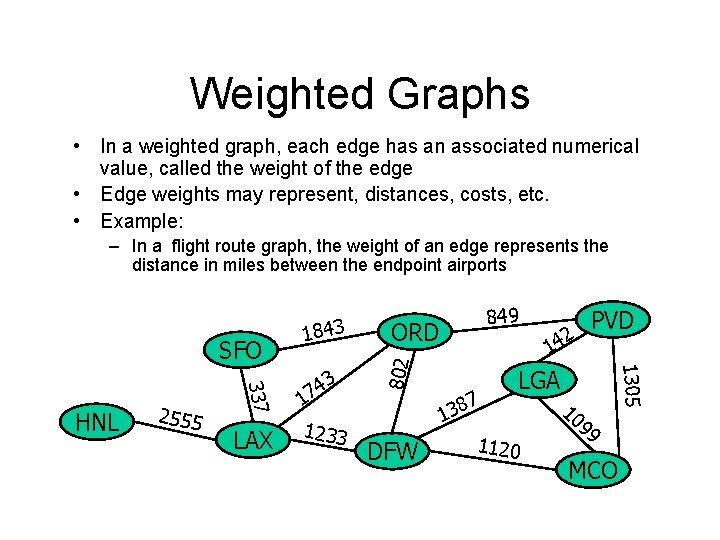
Weighted Graphs • In a weighted graph, each edge has an associated numerical value, called the weight of the edge • Edge weights may represent, distances, costs, etc. • Example: – In a flight route graph, the weight of an edge represents the distance in miles between the endpoint airports LAX 1 1233 ORD 1 7 138 DFW PVD 42 1305 337 HNL 2555 3 4 7 849 802 SFO 1843 LGA 1120 10 99 MCO

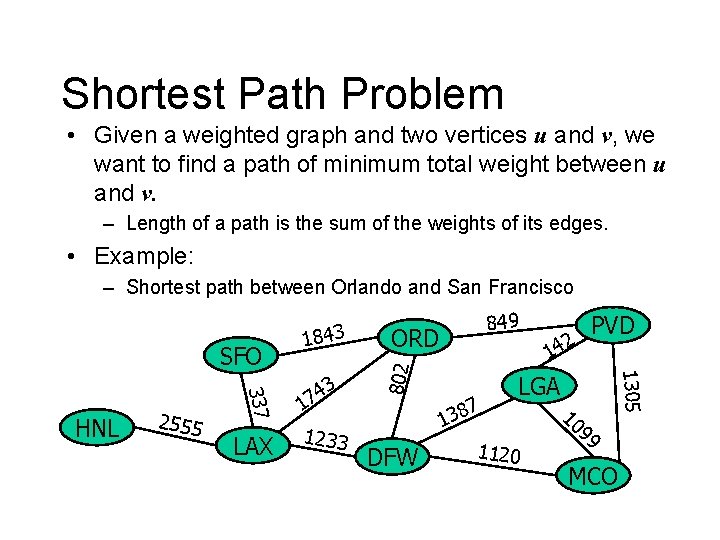
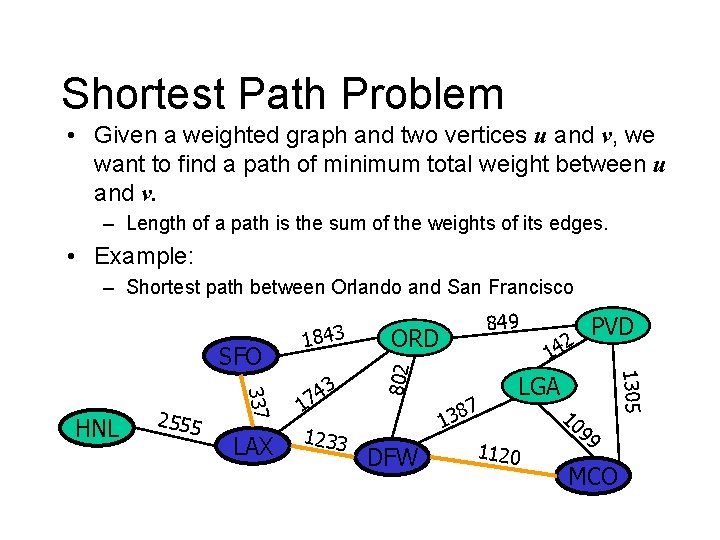
Shortest Path Problem • Given a weighted graph and two vertices u and v, we want to find a path of minimum total weight between u and v. – Length of a path is the sum of the weights of its edges. • Example: – Shortest path between Orlando and San Francisco LAX 1233 DFW 7 8 3 1 2 PVD 14 1305 337 HNL 2555 3 4 7 1 849 ORD 802 SFO 1843 LGA 1120 10 99 MCO

Shortest Path Problem • Given a weighted graph and two vertices u and v, we want to find a path of minimum total weight between u and v. – Length of a path is the sum of the weights of its edges. • Example: – Shortest path between Orlando and San Francisco LAX 1233 DFW 7 8 3 1 2 PVD 14 1305 337 HNL 2555 3 4 7 1 849 ORD 802 SFO 1843 LGA 1120 10 99 MCO

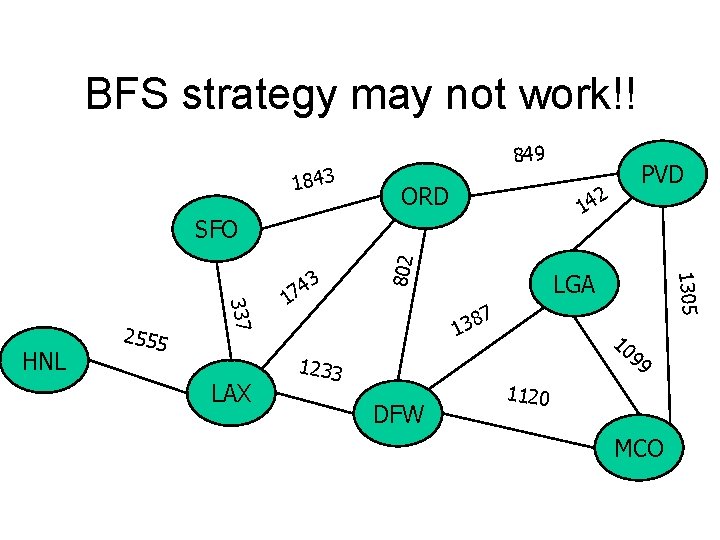
BFS strategy may not work!! 1843 849 ORD 2 14 LAX LGA 7 8 3 1 1233 DFW 1305 337 HNL 2555 1 802 SFO 3 4 7 PVD 10 99 1120 MCO

Dijkstra’s Algorithm for Single source Shortest Path: i. e. shortest path between one vertex and all other vertices. • Extension of Breadth First Search • uses a Greedy algorithm.

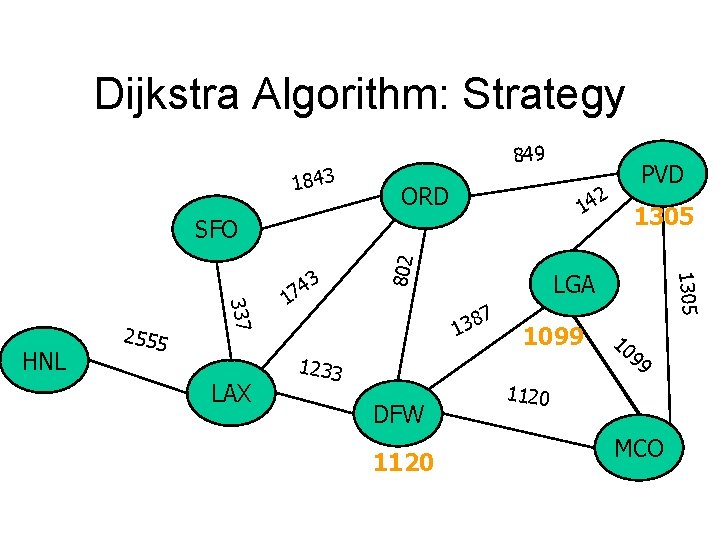
Dijkstra Algorithm: Strategy 1843 849 ORD 2 14 LAX LGA 7 8 3 1 1233 DFW 1120 1305 1099 1305 337 HNL 2555 1 802 SFO 3 4 7 PVD 10 99 1120 MCO

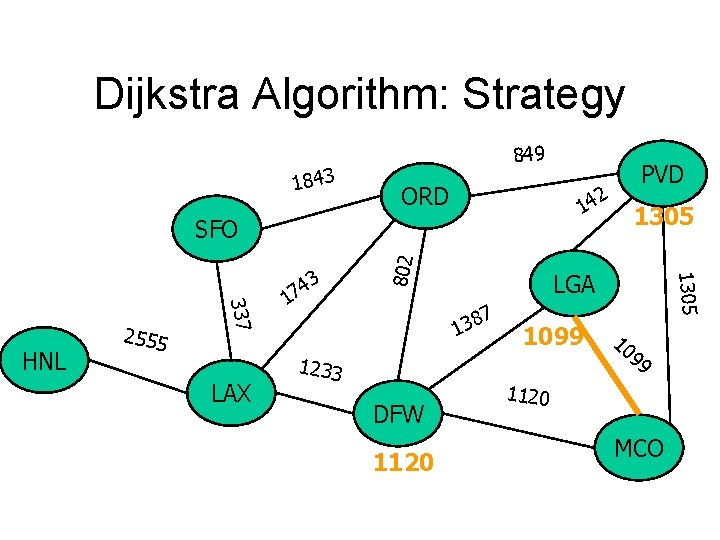
Dijkstra Algorithm: Strategy 1843 849 ORD 2 14 LAX LGA 7 8 3 1 1233 DFW 1120 1305 1099 1305 337 HNL 2555 1 802 SFO 3 4 7 PVD 10 99 1120 MCO

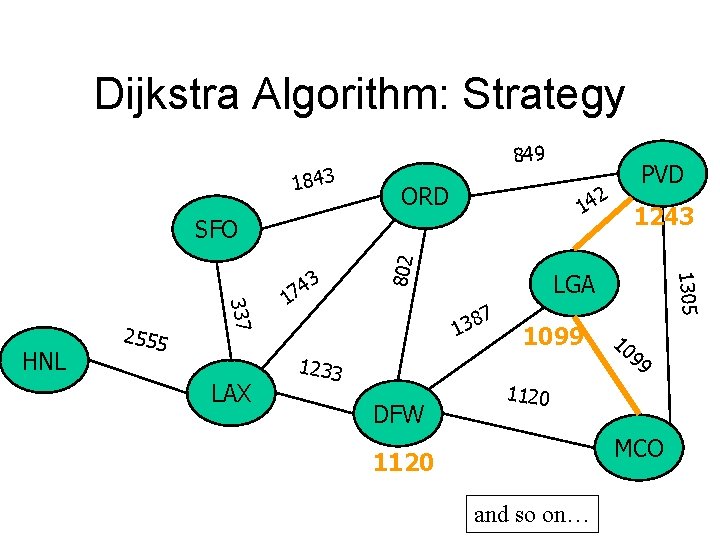
Dijkstra Algorithm: Strategy 1843 849 ORD 2 14 LAX LGA 7 8 3 1 1233 DFW 1243 1099 1305 337 HNL 2555 1 802 SFO 3 4 7 PVD 10 99 1120 MCO 1120 and so on…

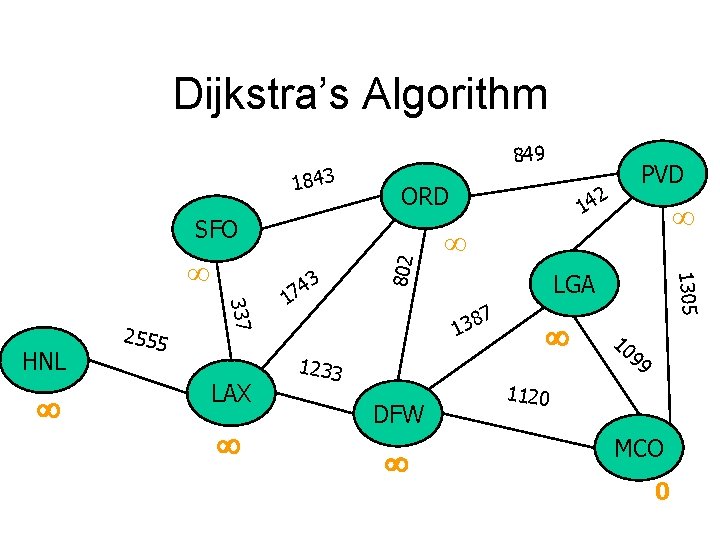
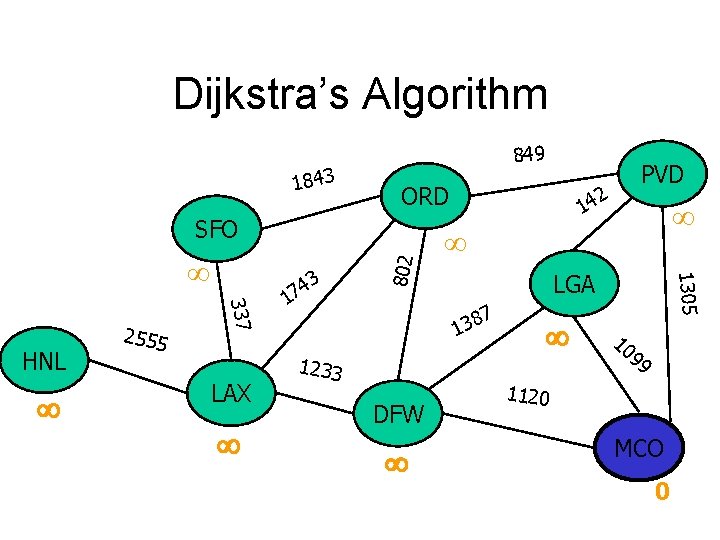
Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 2 14 LGA 7 8 3 1 1233 DFW 1305 802 SFO PVD 10 99 1120 MCO 0

Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 2 14 LGA 7 8 3 1 1233 DFW 1305 802 SFO PVD 10 99 1120 MCO 0

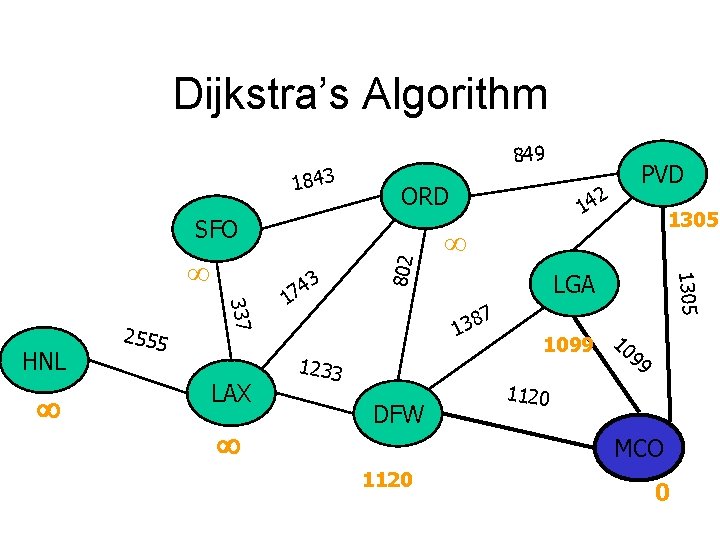
Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 14 LGA 7 8 3 1 1233 DFW 1305 802 SFO 2 PVD 1099 109 9 1120 MCO 1120 0

Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 14 LGA 7 8 3 1 1233 DFW 1305 802 SFO 2 PVD 1099 10 99 1120 MCO 1120 0

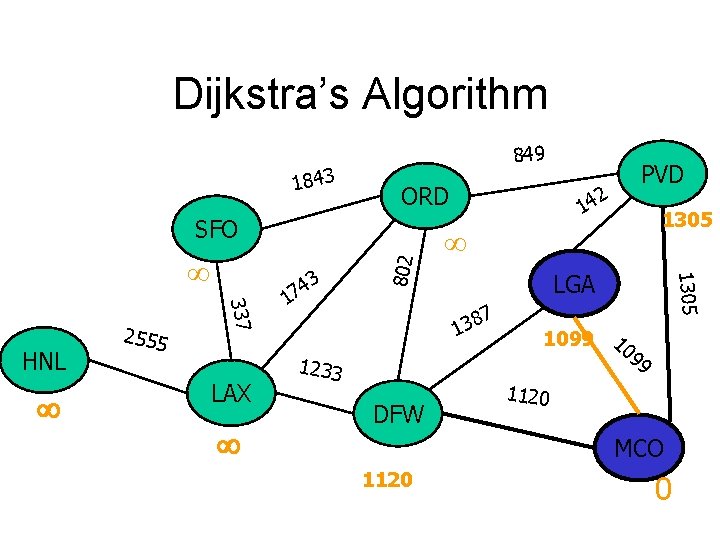
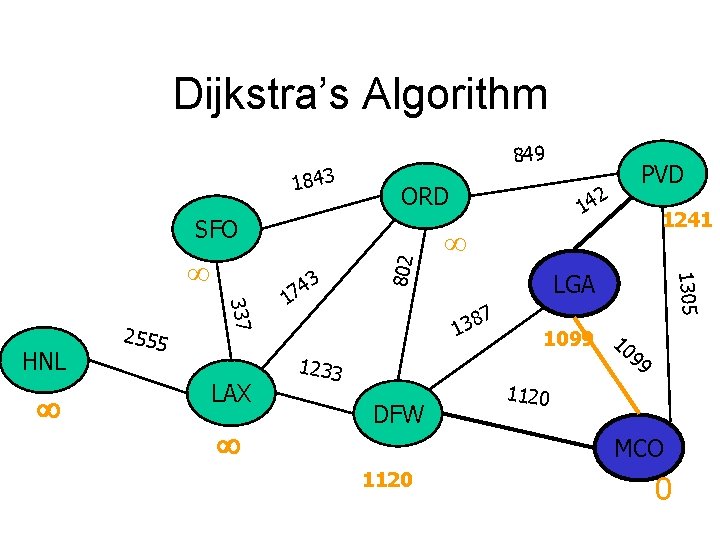
Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 14 LGA 7 8 3 1 1233 DFW 1241 1305 802 SFO 2 PVD 1099 10 99 1120 MCO 1120 0

Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 14 LGA 7 8 3 1 1233 DFW 1241 1305 802 SFO 2 PVD 1099 10 99 1120 MCO 1120 0

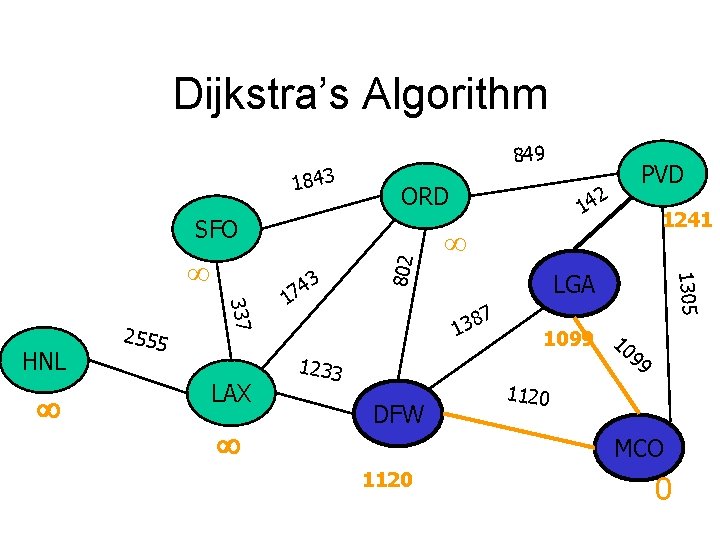
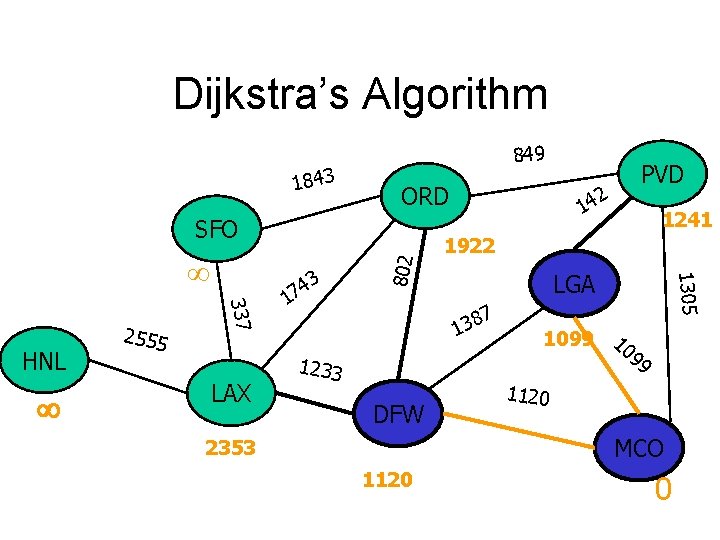
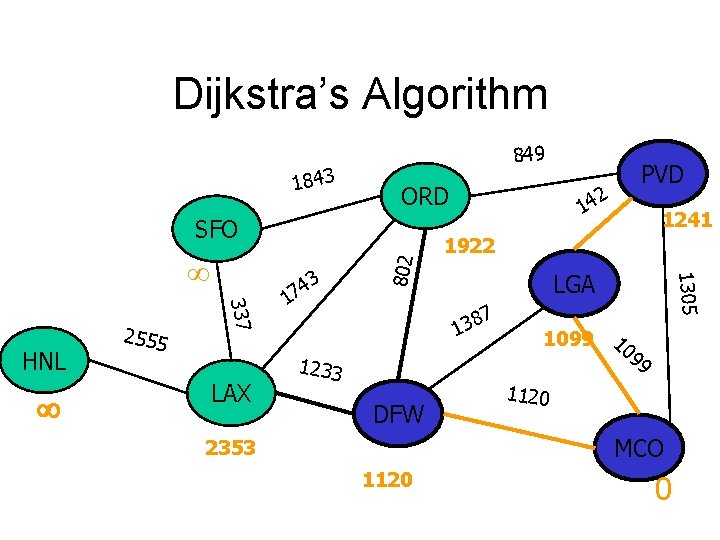
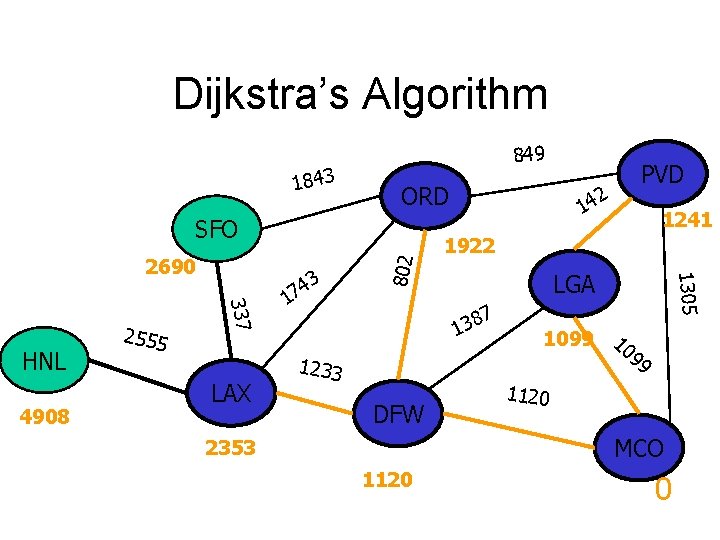
Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 14 1922 LGA 7 8 3 1 1233 DFW 1241 1305 802 SFO 2 PVD 1099 10 99 1120 MCO 2353 1120 0

Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 14 1922 LGA 7 8 3 1 1233 DFW 1241 1305 802 SFO 2 PVD 1099 10 99 1120 MCO 2353 1120 0

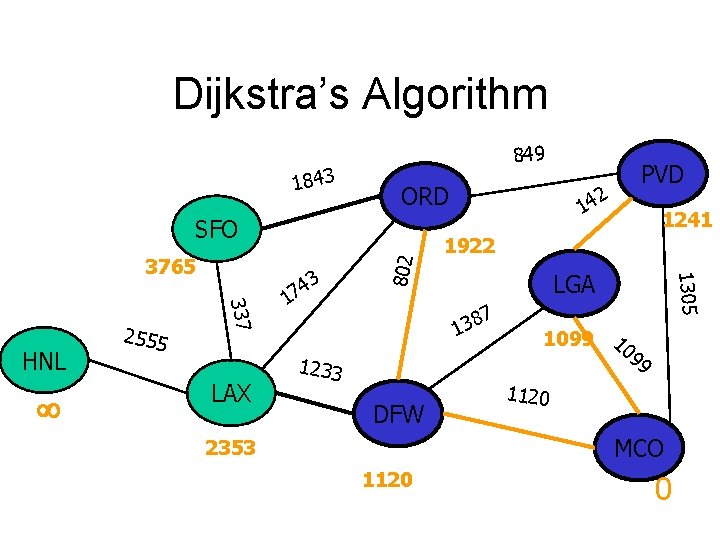
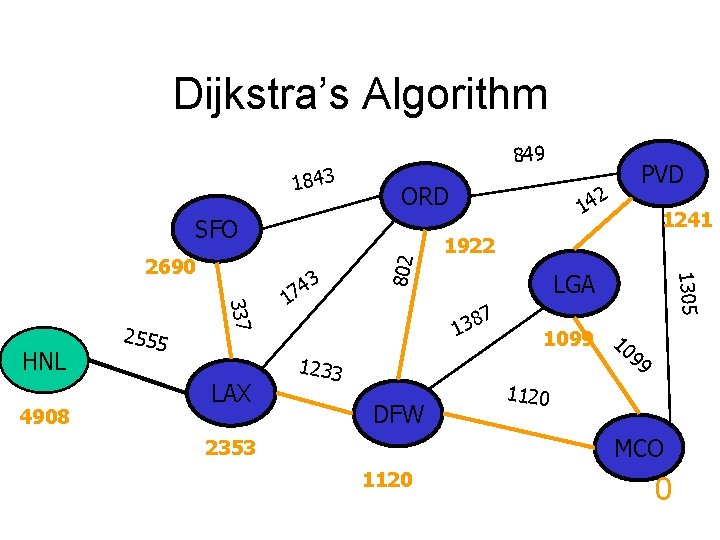
Dijkstra’s Algorithm 1843 849 ORD 337 HNL 2555 LAX 3 4 7 1 14 1922 LGA 7 8 3 1 1233 DFW 1241 1305 3765 802 SFO 2 PVD 1099 10 99 1120 MCO 2353 1120 0

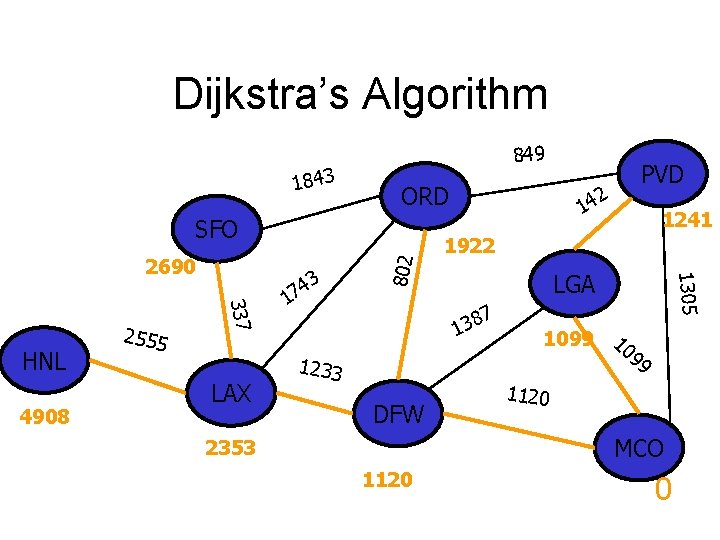
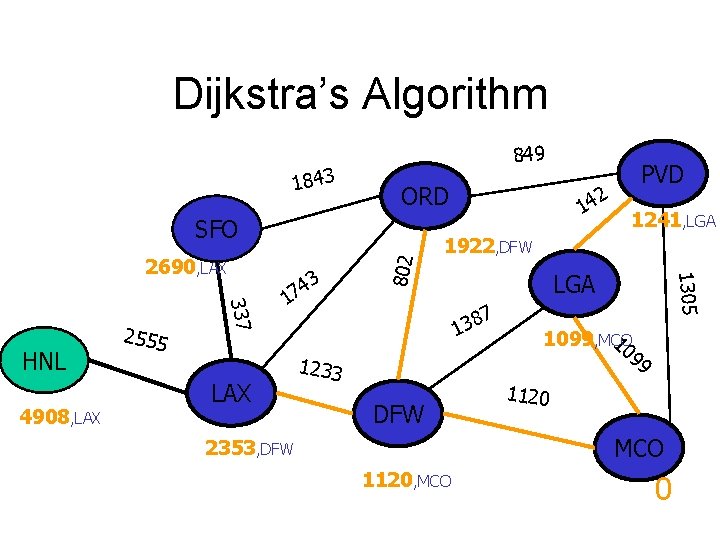
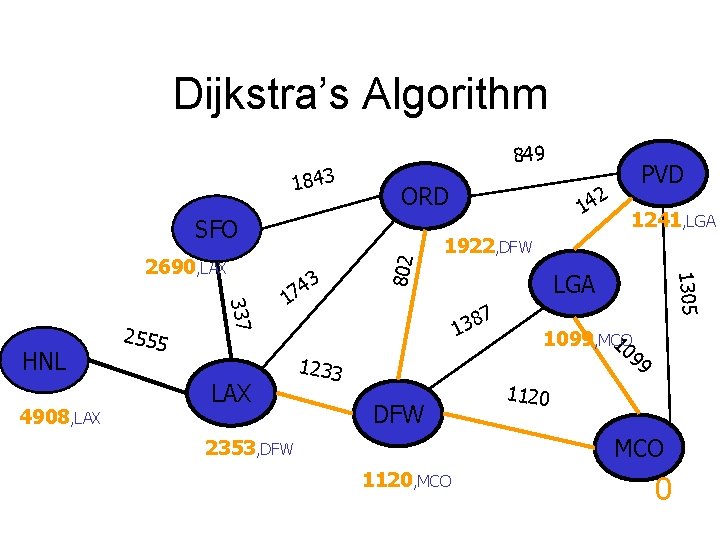
Dijkstra’s Algorithm 1843 849 ORD 4908 337 HNL 2555 LAX 3 4 7 1 14 1922 LGA 7 8 3 1 1233 DFW 1241 1305 2690 802 SFO 2 PVD 1099 10 99 1120 MCO 2353 1120 0

Dijkstra’s Algorithm 1843 849 ORD 4908 337 HNL 2555 LAX 3 4 7 1 14 1922 LGA 7 8 3 1 1233 DFW 1241 1305 2690 802 SFO 2 PVD 1099 10 99 1120 MCO 2353 1120 0

Dijkstra’s Algorithm 1843 849 ORD 4908 337 HNL 2555 LAX 3 4 7 1 14 1922 LGA 7 8 3 1 1233 DFW 1241 1305 2690 802 SFO 2 PVD 1099 10 99 1120 MCO 2353 1120 0

Dijkstra’s Algorithm • How to Find shortest path and shortest path length?

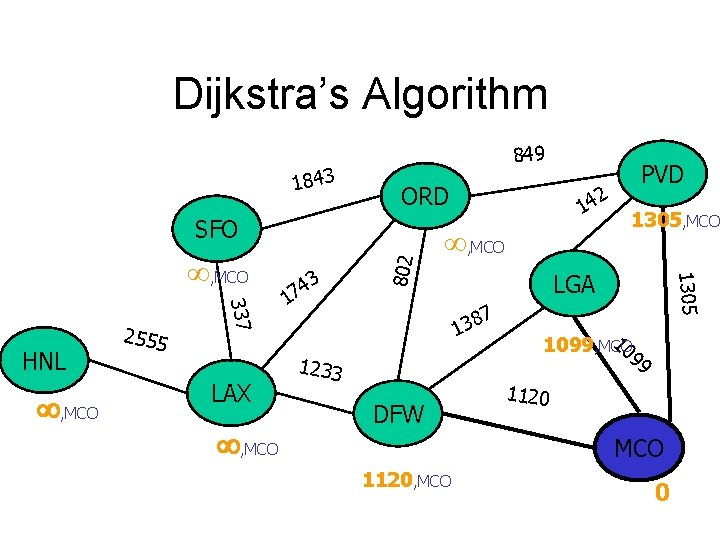
Dijkstra’s Algorithm 1843 849 ORD , MCO 337 HNL 2555 LAX , MCO 3 4 7 1 2 14 , MCO LGA 7 8 3 1 1305 , MCO 802 SFO PVD , MCO 109 9 1233 DFW , MCO 1120 MCO 0

Dijkstra’s Algorithm 1843 849 ORD , MCO 337 HNL 2555 LAX , MCO 3 4 7 1 2 14 , MCO 1305, MCO LGA 7 8 3 1 1305 , MCO 802 SFO PVD 10 1099, MCO 9 9 1233 DFW 1120 MCO 1120, MCO 0

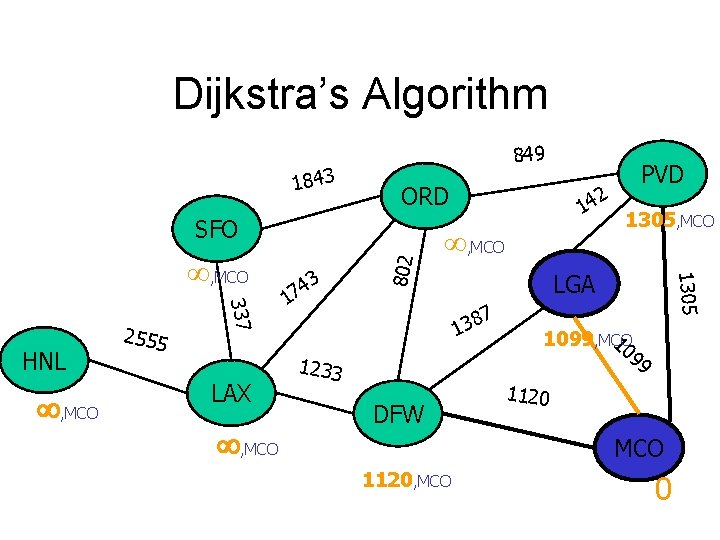
Dijkstra’s Algorithm 1843 849 ORD , MCO 337 HNL 2555 LAX , MCO 3 4 7 1 , MCO LGA 7 8 3 1 1233 DFW 1305, MCO 1305 , MCO 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 1120, MCO 0

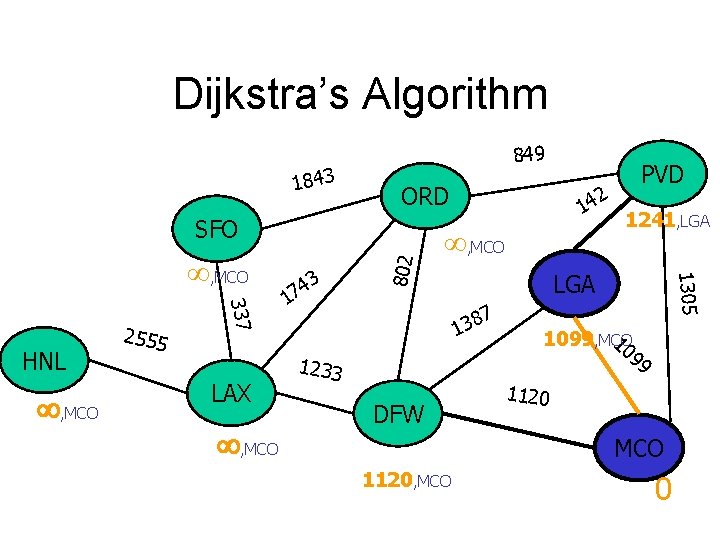
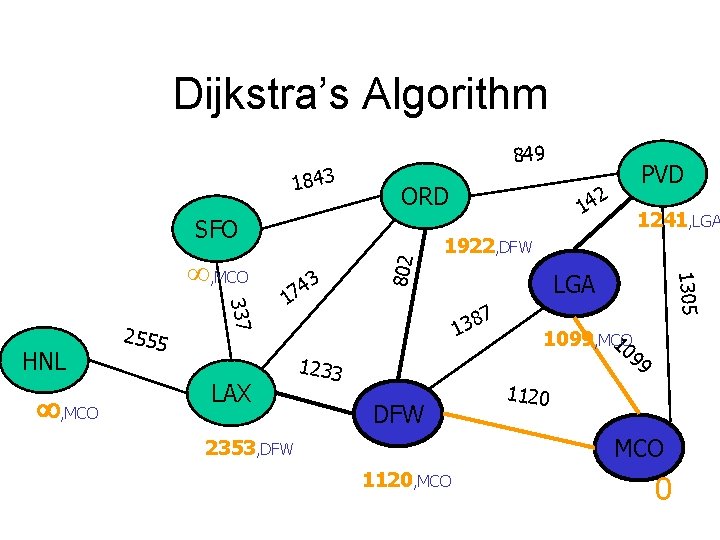
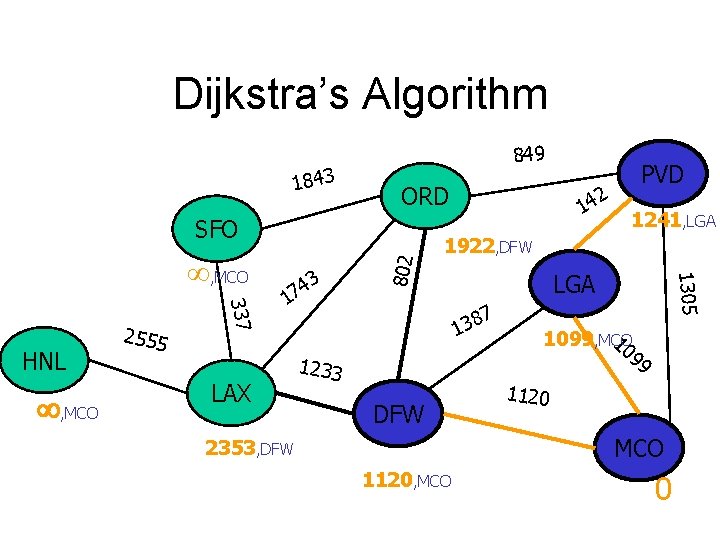
Dijkstra’s Algorithm 1843 849 ORD , MCO 337 HNL 2555 LAX , MCO 3 4 7 1 , MCO LGA 7 8 3 1 1233 DFW 1241, LGA 1305 , MCO 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 1120, MCO 0

Dijkstra’s Algorithm 1843 849 ORD , MCO 337 HNL 2555 LAX , MCO 3 4 7 1 , MCO LGA 7 8 3 1 1233 DFW 1241, LGA 1305 , MCO 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 1120, MCO 0

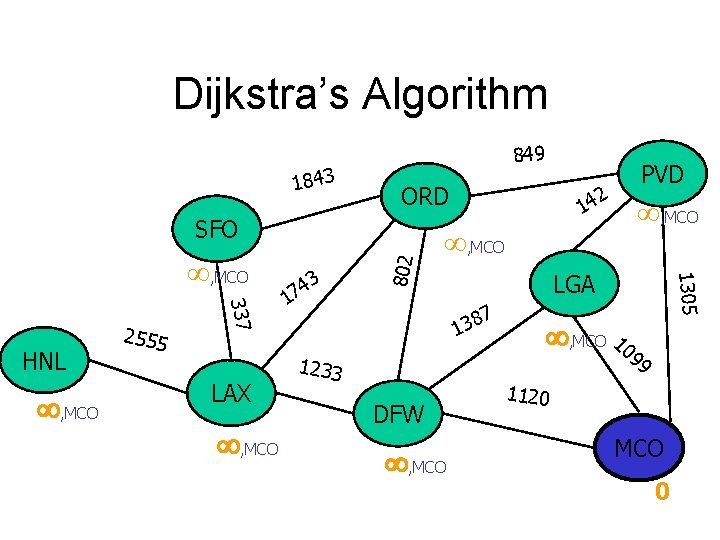
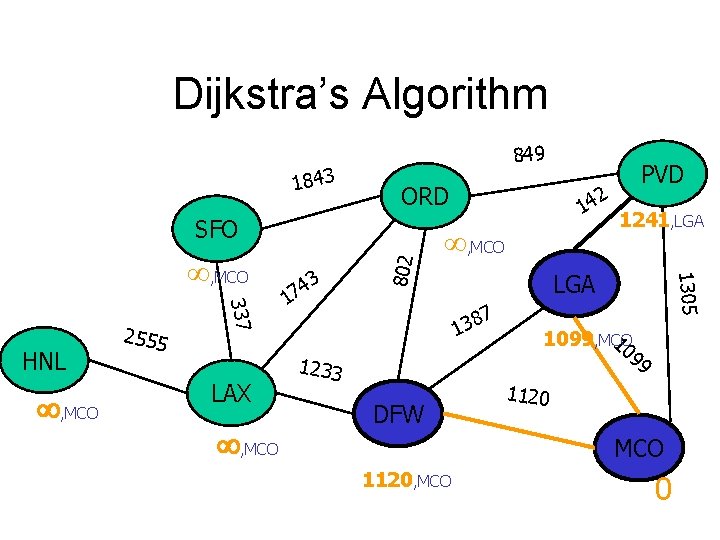
Dijkstra’s Algorithm 1843 849 ORD , MCO 337 HNL 2555 3 4 7 1 LAX 1241, LGA 1922, DFW LGA 7 8 3 1 1233 DFW 1305 , MCO 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 2353, DFW 1120, MCO 0

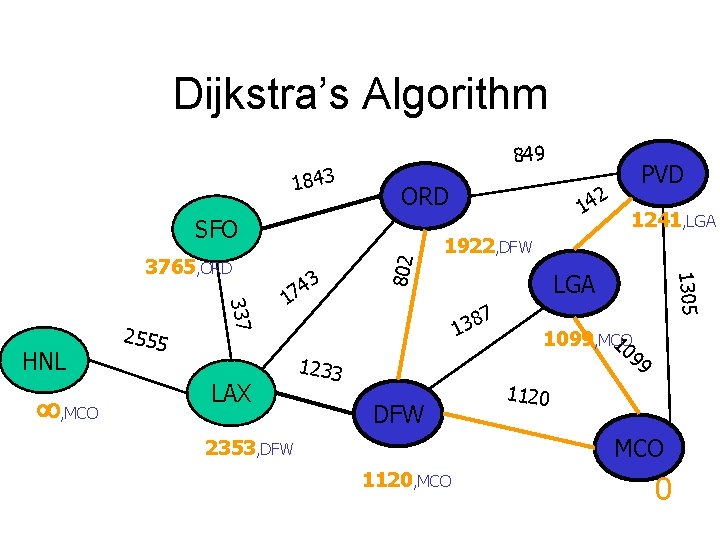
Dijkstra’s Algorithm 1843 849 ORD , MCO 337 HNL 2555 3 4 7 1 LAX 1241, LGA 1922, DFW LGA 7 8 3 1 1233 DFW 1305 , MCO 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 2353, DFW 1120, MCO 0

Dijkstra’s Algorithm 1843 849 ORD , MCO 337 HNL 2555 3 4 7 1 LAX 1241, LGA 1922, DFW LGA 7 8 3 1 1233 DFW 1305 3765, ORD 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 2353, DFW 1120, MCO 0

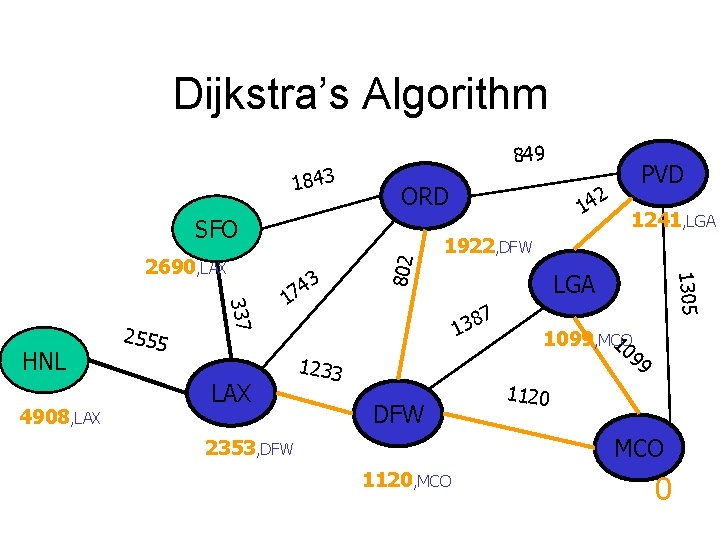
Dijkstra’s Algorithm 1843 849 ORD 4908, LAX 337 HNL 2555 3 4 7 1 LAX 1241, LGA 1922, DFW LGA 7 8 3 1 1233 DFW 1305 2690, LAX 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 2353, DFW 1120, MCO 0

Dijkstra’s Algorithm 1843 849 ORD 4908, LAX 337 HNL 2555 3 4 7 1 LAX 1241, LGA 1922, DFW LGA 7 8 3 1 1233 DFW 1305 2690, LAX 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 2353, DFW 1120, MCO 0

Dijkstra’s Algorithm 1843 849 ORD 4908, LAX 337 HNL 2555 3 4 7 1 LAX 1241, LGA 1922, DFW LGA 7 8 3 1 1233 DFW 1305 2690, LAX 802 SFO 2 14 PVD 10 1099, MCO 99 1120 MCO 2353, DFW 1120, MCO 0

Dijkstra’s Algorithm Shortest. Path (G, s) Q new priority queue for all v G. vertices() if v = s v. distance 0 O(n log n) else v. distance v. parent s Q. en. Queue(v. distance, v) while Q. is. Empty() O(n log n) v Q. remove. Min() v. path. Known true for all e G. incident. Edges(v) w opposite(v, e) if w. path. Known O(m log n) if v. distance + weight(e) < w. distance v. distance + weight(e) w. parent v O((n+m)log n) update key of w in Q

Analysis • Graph operations – Method incident. Edges is called once for each vertex • Label operations – We set/get the distance and locator labels of vertex w O(n) times – Setting/getting a label takes O(1) time • Priority queue operations – Each vertex is inserted once into and removed once from the priority queue, where each insertion or removal takes O(log n) time – The key of a vertex in the priority queue is modified at most deg(w) times, where each key change takes O(log n) time • Dijkstra’s algorithm runs in O((n + m) log n) time provided the graph is represented by the adjacency list structure – Recall that Sv deg(v) = 2 m • The running time can also be expressed as O(m log n) since the graph is connected

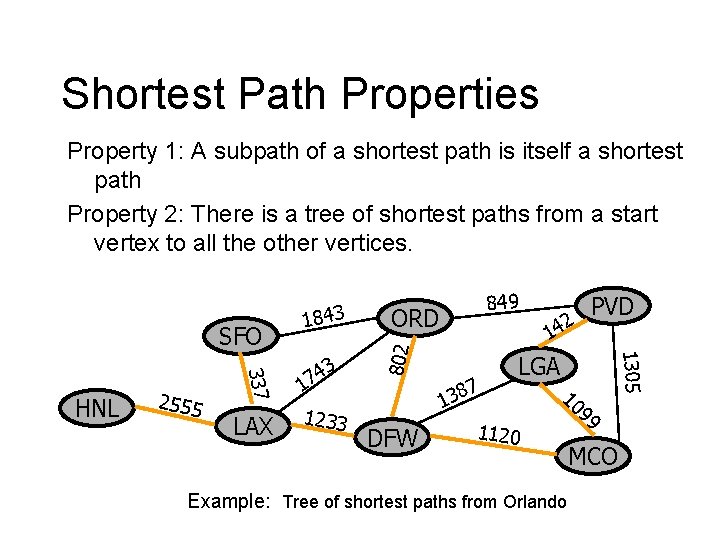
Shortest Path Properties Property 1: A subpath of a shortest path is itself a shortest path Property 2: There is a tree of shortest paths from a start vertex to all the other vertices. LAX 1233 DFW 7 8 3 1 2 PVD 14 1305 337 HNL 2555 3 4 17 849 ORD 802 SFO 1843 LGA 10 1120 Example: Tree of shortest paths from Orlando 99 MCO

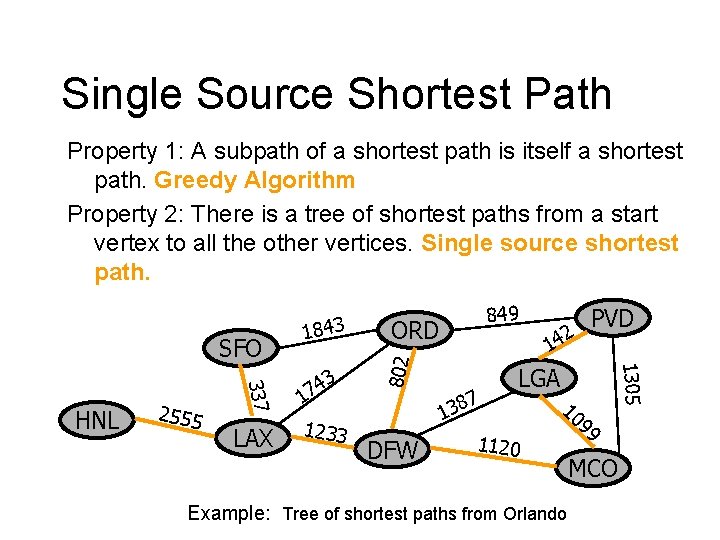
Single Source Shortest Path Property 1: A subpath of a shortest path is itself a shortest path. Greedy Algorithm Property 2: There is a tree of shortest paths from a start vertex to all the other vertices. Single source shortest path. LAX 1233 DFW 7 8 3 1 2 PVD 14 1305 337 HNL 2555 3 4 17 849 ORD 802 SFO 1843 LGA 10 1120 Example: Tree of shortest paths from Orlando 99 MCO

Why It Doesn’t Work for Negative-Weight Edges Dijkstra’s algorithm is based on the greedy method. It adds vertices by increasing distance. – If a node with a negative incident edge were to be added late to the vertex list for which decisions have been made, it could mess up distances for vertices already in the list.