Review Surface Area SA of Right Rectangular Prisms

Review: Surface Area (SA) of Right Rectangular Prisms and Cylinders

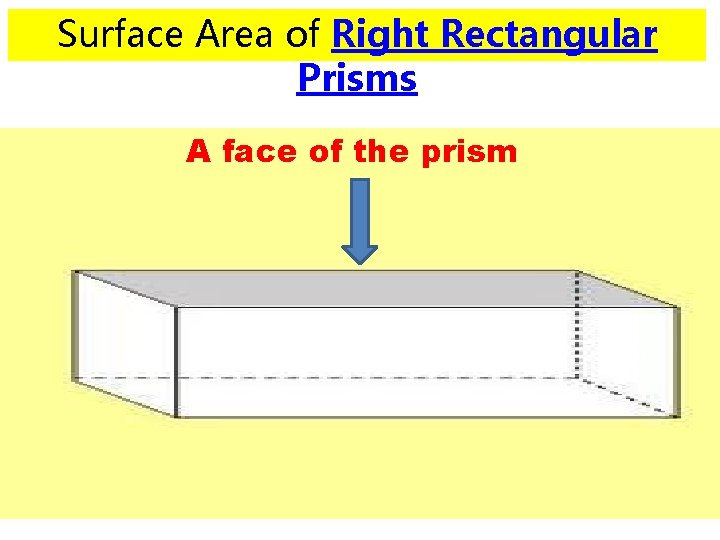
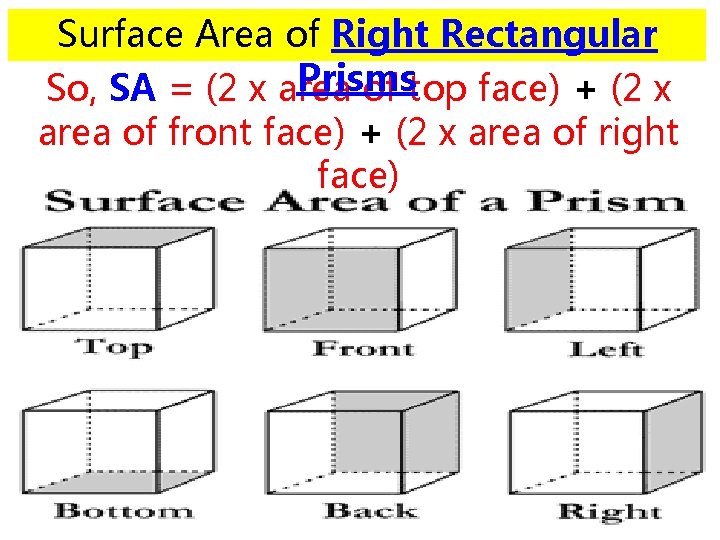
Surface Area of Right Rectangular Prisms A face of the prism

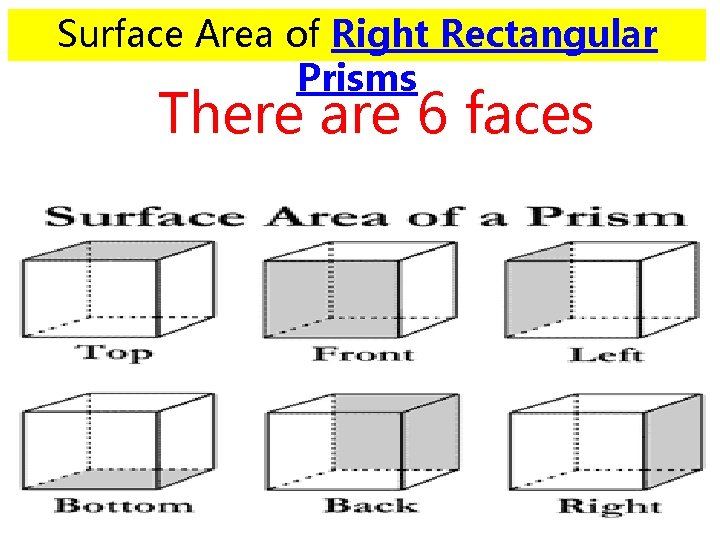
Surface Area of Right Rectangular Prisms There are 6 faces

Surface Area of Right Rectangular Prisms SA is the sum of the areas of its faces

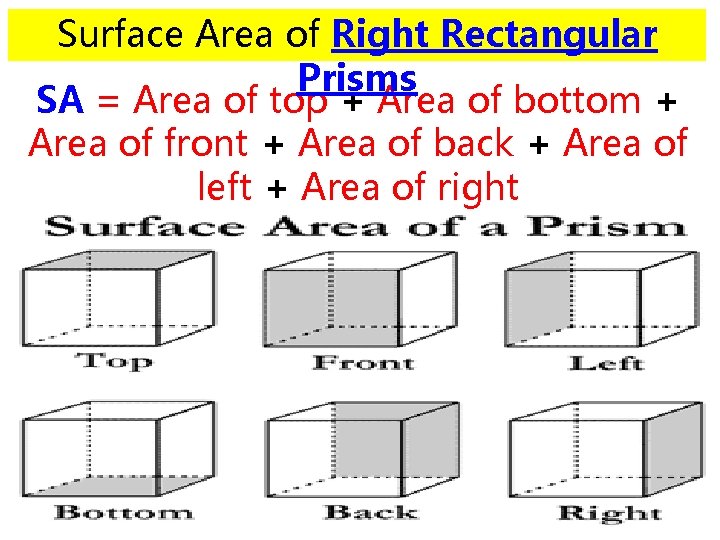
Surface Area of Right Rectangular Prisms SA = Area of top + Area of bottom + Area of front + Area of back + Area of left + Area of right

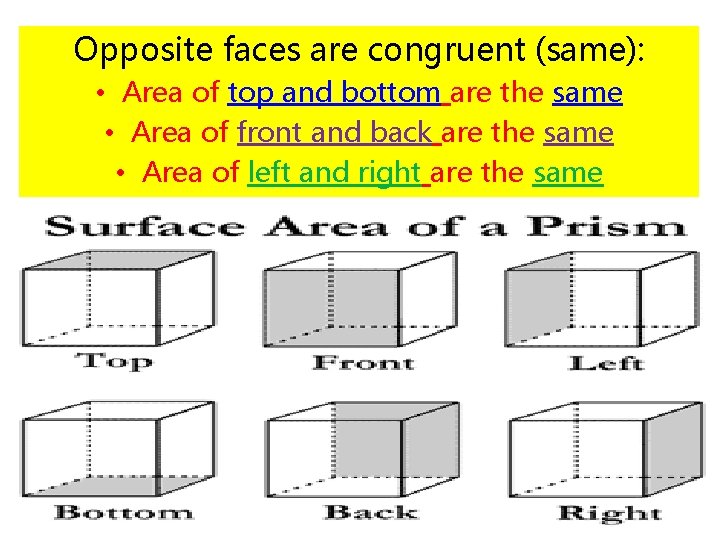
Opposite faces are congruent (same): • Area of top and bottom are the same • Area of front and back are the same • Area of left and right are the same

Surface Area of Right Rectangular Prisms So, SA = (2 x area of top face) + (2 x area of front face) + (2 x area of right face)

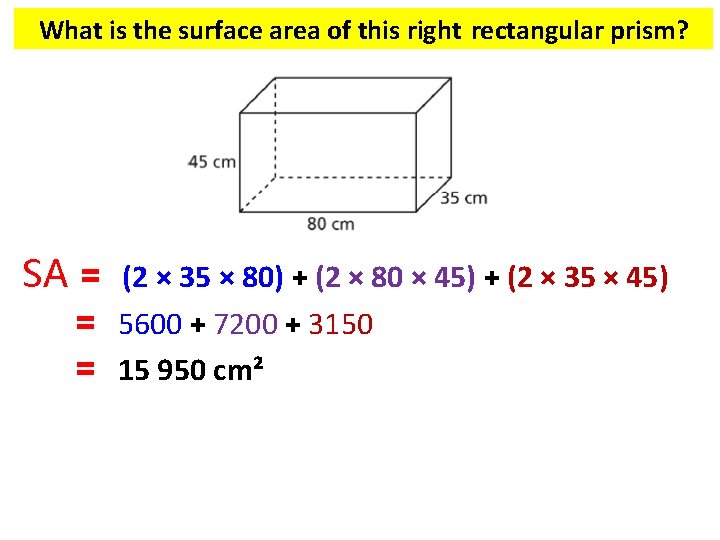
What is the surface area of this right rectangular prism? SA = (2 × 35 × 80) + (2 × 80 × 45) + (2 × 35 × 45) = 5600 + 7200 + 3150 = 15 950 cm²

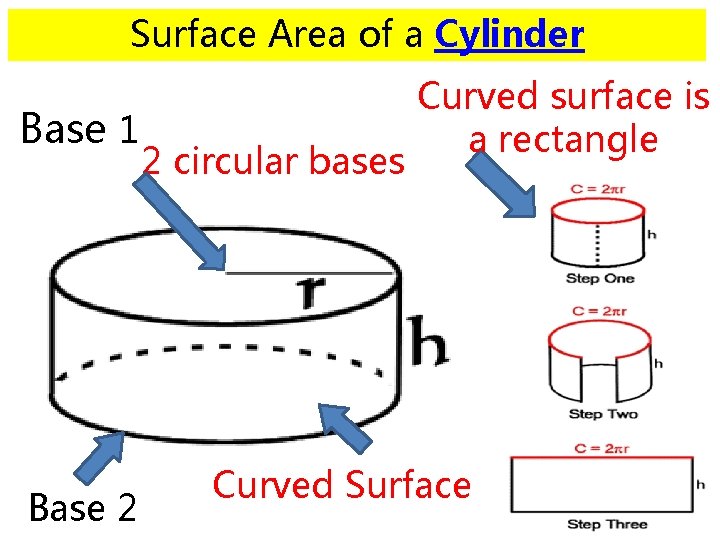
Surface Area of a Cylinder Base 1 Base 2 2 circular bases Curved surface is a rectangle Curved Surface

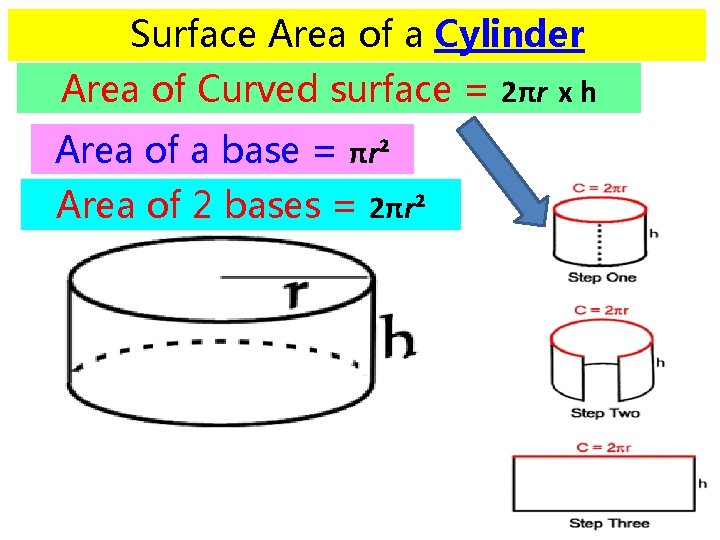
Surface Area of a Cylinder Area of Curved surface = 2πr x h Area of a base = πr² Area of 2 bases = 2πr²

Surface Area of a Cylinder Area of Curved surface = 2πr x h Area of a base = πr² Area of 2 bases = 2πr² SA of a cylinder = (2πr x h) + 2πr²

What is the surface area, SA, of this right cylinder? SA = 2πr² + 2πrh =(2 × π × 2²) + (2 × π × 2 × 5) ≈ 87. 9645 cm²

Review: Volume (V) of Right Rectangular Prisms and Cylinders A face of the prism

Volume (V) of Right Rectangular Prisms Volume is a space occupied by the prism

Volume (V) of Right Rectangular Prisms = (Area of the bottom face) =Axh x (height)

Determine the volume of this right rectangular prism V = A×h = (4. 0 × 6. 0) x 1. 5 = 24. 0 × 1. 5 = 36. 0 m³

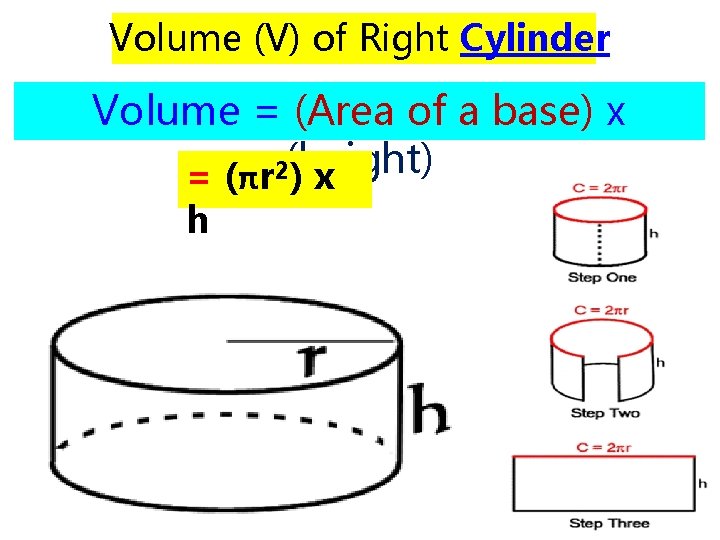
Volume (V) of Right Cylinder Volume = (Area of a base) x (height) = (πr²) x h

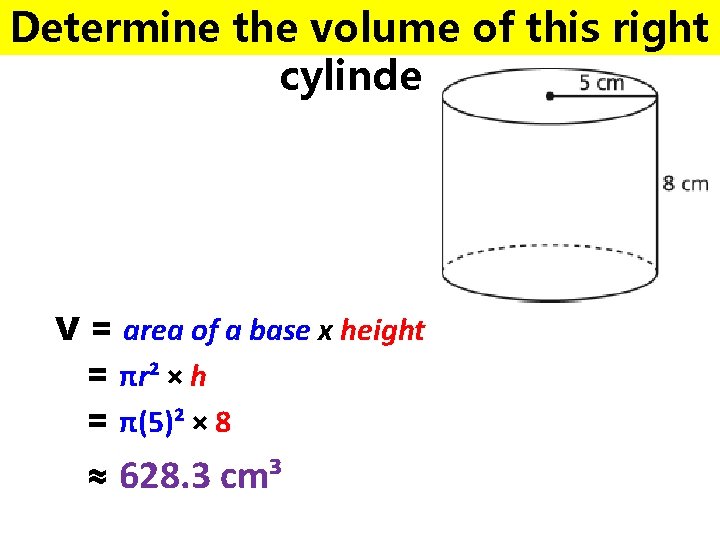
Determine the volume of this right cylinder V = area of a base x height = πr² × h = π(5)² × 8 ≈ 628. 3 cm³

A Worksheet: Finish both sides by tomorrow

1. 4 Surface Areas of Right Pyramids and Right Cones

Build Your Pyramids!

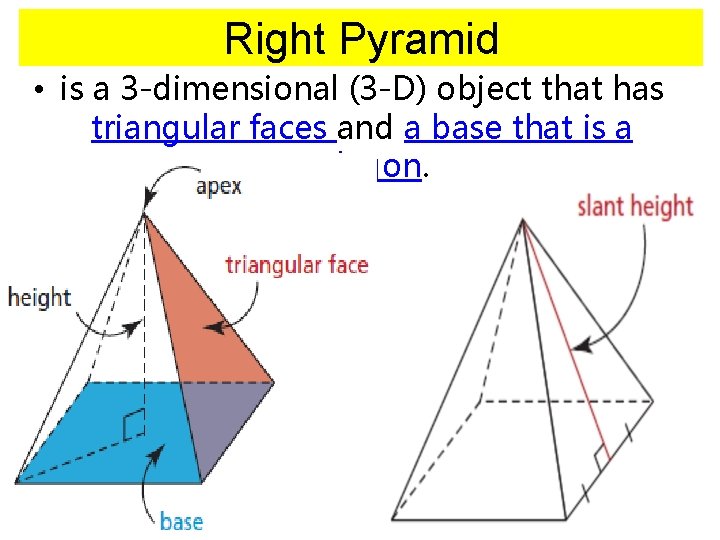
Right Pyramid • is a 3 -dimensional (3 -D) object that has triangular faces and a base that is a polygon.

• WHAT IS A is a 3 -dimensional (3 -D) object that has POLYGON? triangular faces and a base that is a polygon.

WHAT IS A Polygons. POLYGON? are 2 -dimensional shapes. • • They are made of straight lines, and the shape is "closed" (all the lines connect ). Polygon (straight sides) Not a Polygon (has a curve) Not a Polygon (open, not closed)

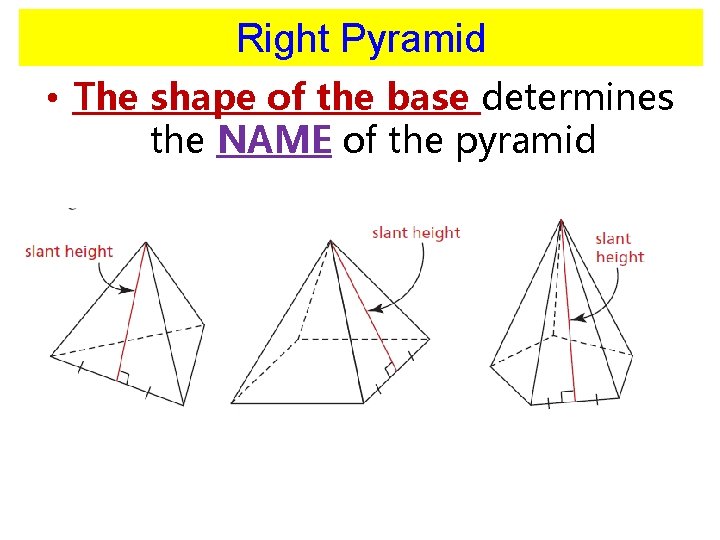
Right Pyramid • The shape of the base determines the NAME of the pyramid

Right Pyramid • MUST know the vocabulary! • Apex = a point where triangular faces meet • Slant height = a height of a triangular face

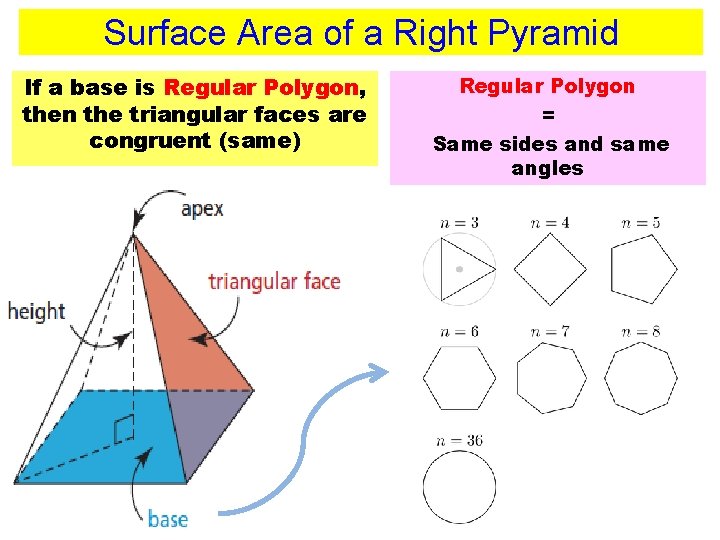
Surface Area of a Right Pyramid If a base is Regular Polygon, then the triangular faces are congruent (same) Regular Polygon = Same sides and same angles

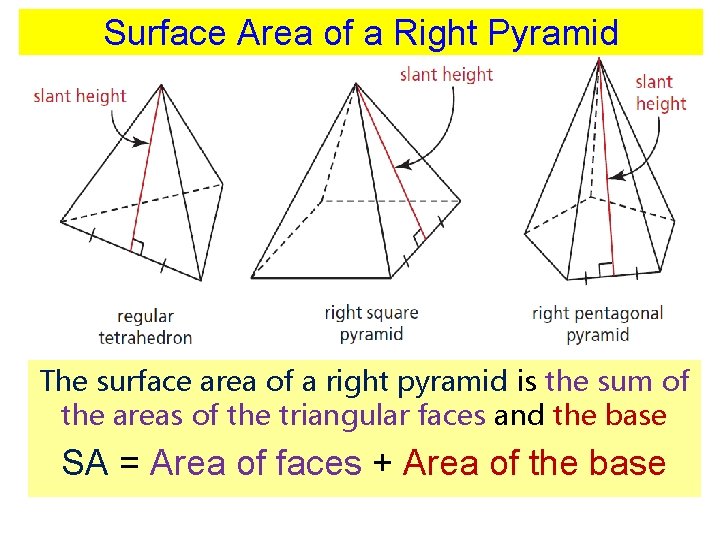
Surface Area of a Right Pyramid The surface area of a right pyramid is the sum of the areas of the triangular faces and the base SA = Area of faces + Area of the base

Surface Area of a Right Pyramid The surface area of a right pyramid is the sum of the areas of the triangular faces and the base SA = Area of faces + Area of the base A review question!!! WHAT IS THE AREA OF A TRIANGLE?

Surface Area of a Right Pyramid • The surface area of a right pyramid is the sum of the areas of the triangular faces and the base • SA = Area of faces x Area of the base • REVIEW!!! • WHAT IS THE AREA OF A TRIANGLE?

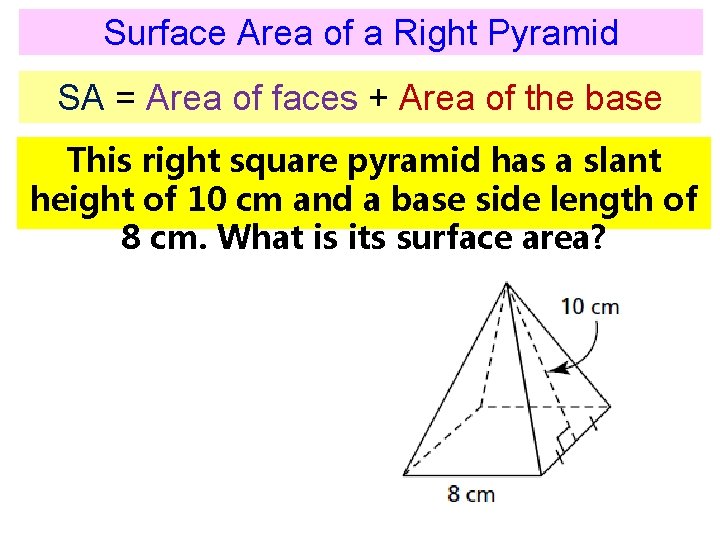
Surface Area of a Right Pyramid SA = Area of faces + Area of the base This right square pyramid has a slant height of 10 cm and a base side length of 8 cm. What is its surface area?

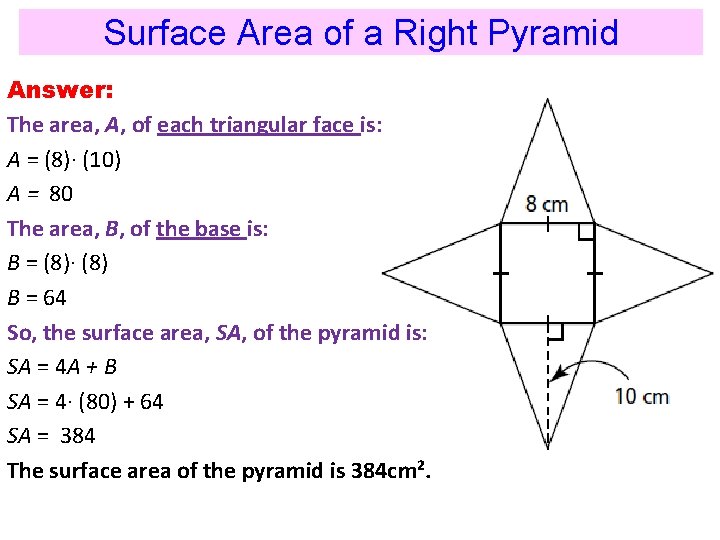
Surface Area of a Right Pyramid Answer: The area, A, of each triangular face is: A = (8)· (10) A = 80 The area, B, of the base is: B = (8)· (8) B = 64 So, the surface area, SA, of the pyramid is: SA = 4 A + B SA = 4· (80) + 64 SA = 384 The surface area of the pyramid is 384 cm².

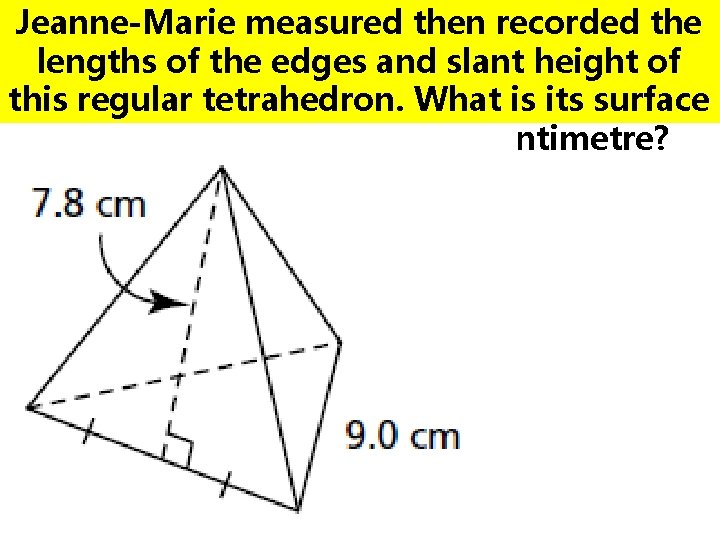
Jeanne-Marie measured then recorded the lengths of the edges and slant height of this regular tetrahedron. What is its surface area to the nearest square centimetre?

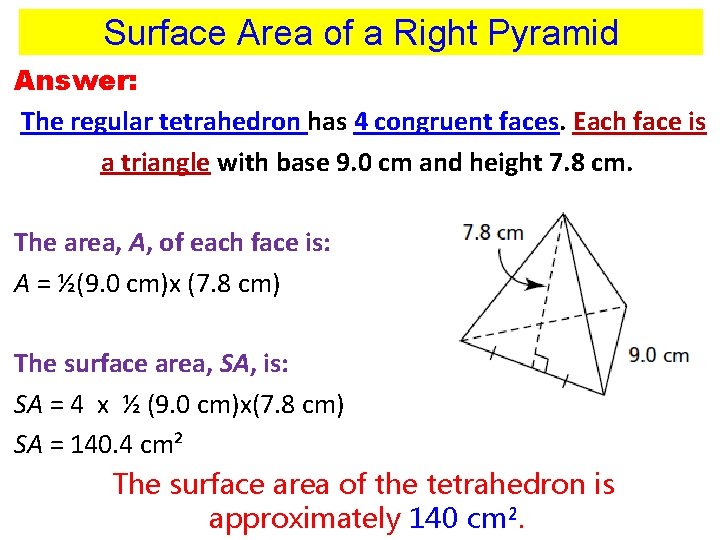
Surface Area of a Right Pyramid Answer: The regular tetrahedron has 4 congruent faces. Each face is a triangle with base 9. 0 cm and height 7. 8 cm. The area, A, of each face is: A = ½(9. 0 cm)x (7. 8 cm) The surface area, SA, is: SA = 4 x ½ (9. 0 cm)x(7. 8 cm) SA = 140. 4 cm² The surface area of the tetrahedron is approximately 140 cm².

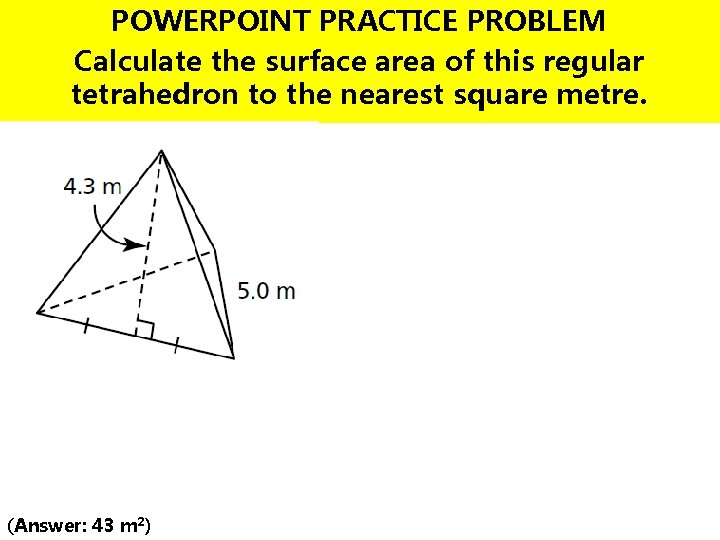
POWERPOINT PRACTICE PROBLEM Calculate the surface area of this regular tetrahedron to the nearest square metre. (Answer: 43 m 2)

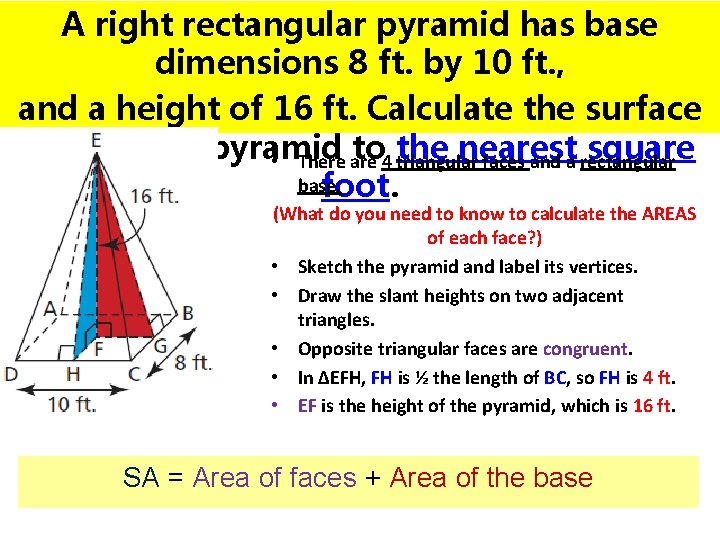
A right rectangular pyramid has base dimensions 8 ft. by 10 ft. , and a height of 16 ft. Calculate the surface area of the pyramid to 4 the nearest square • There are triangular faces and a rectangular base. foot. (What do you need to know to calculate the AREAS of each face? ) • Sketch the pyramid and label its vertices. • Draw the slant heights on two adjacent triangles. • Opposite triangular faces are congruent. • In ∆EFH, FH is ½ the length of BC, so FH is 4 ft. • EF is the height of the pyramid, which is 16 ft. SA = Area of faces + Area of the base

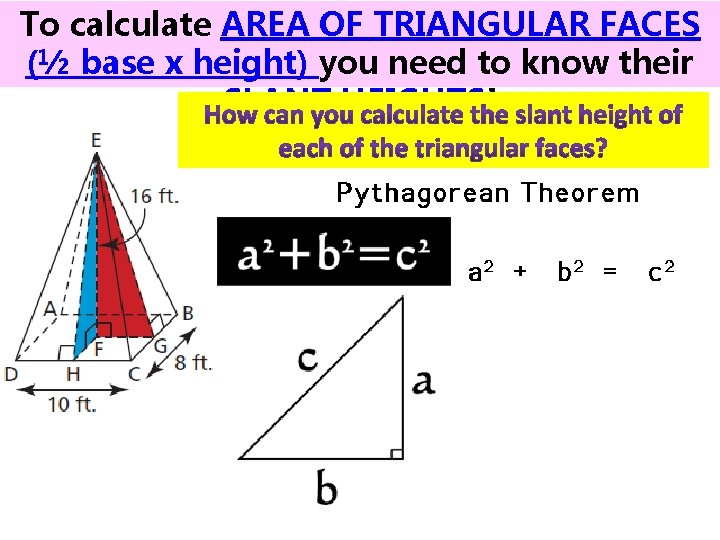
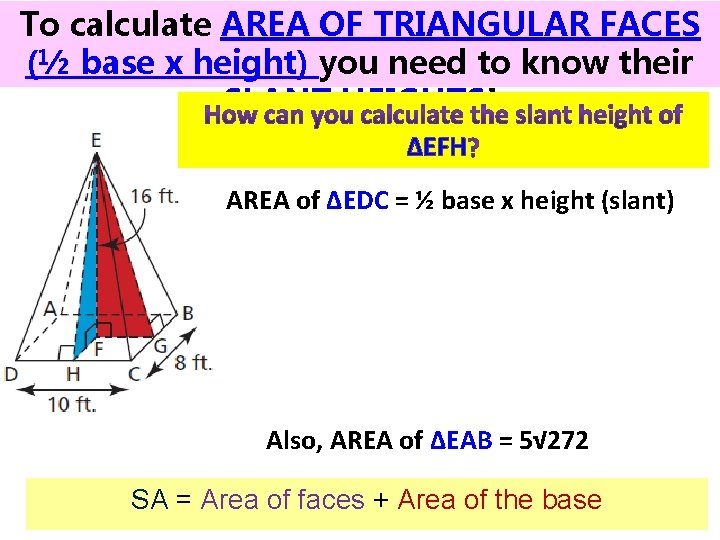
To calculate AREA OF TRIANGULAR FACES (½ base x height) you need to know their SLANT HEIGHTS!

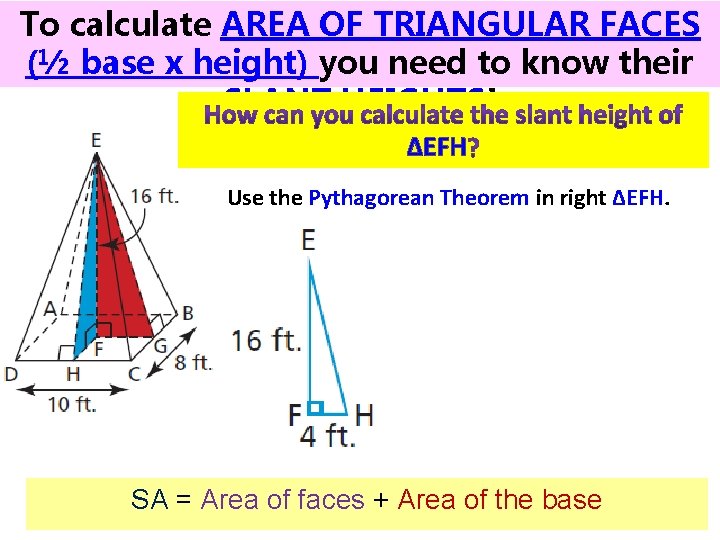
To calculate AREA OF TRIANGULAR FACES (½ base x height) you need to know their SLANT HEIGHTS! ∆EFH Use the Pythagorean Theorem in right ∆EFH. SA = Area of faces + Area of the base

To calculate AREA OF TRIANGULAR FACES (½ base x height) you need to know their SLANT HEIGHTS! ∆EFH AREA of ∆EDC = ½ base x height (slant) Also, AREA of ∆EAB = 5√ 272 SA = Area of faces + Area of the base

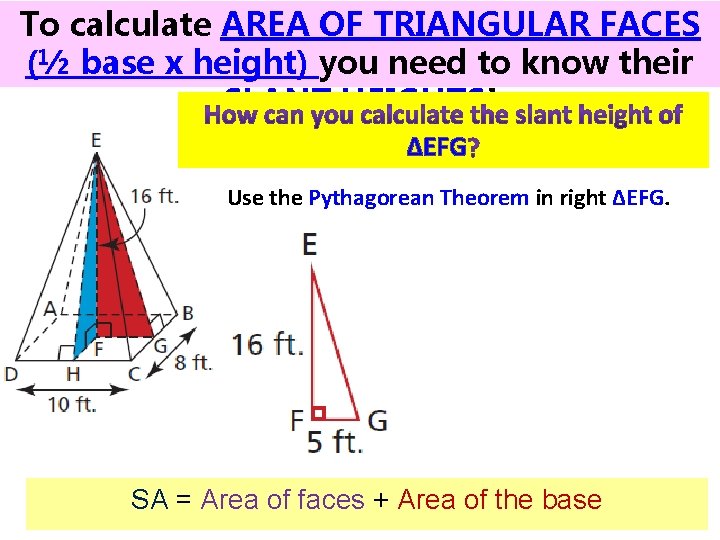
To calculate AREA OF TRIANGULAR FACES (½ base x height) you need to know their SLANT HEIGHTS! ∆EFG Use the Pythagorean Theorem in right ∆EFG. SA = Area of faces + Area of the base

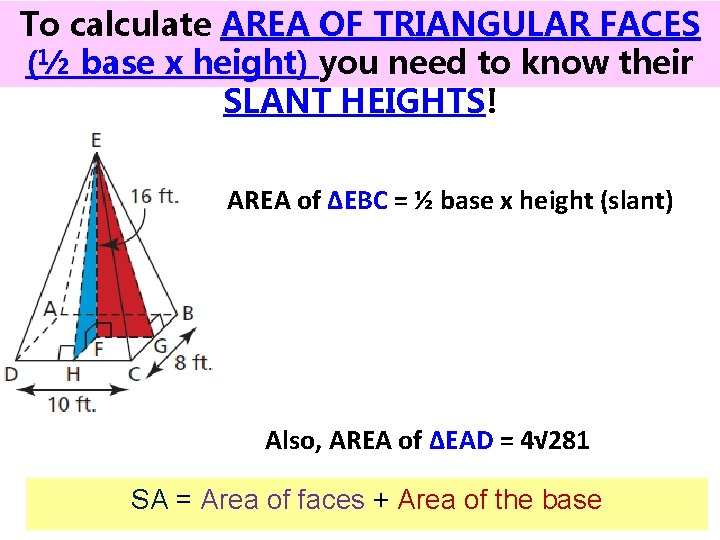
To calculate AREA OF TRIANGULAR FACES (½ base x height) you need to know their SLANT HEIGHTS! AREA of ∆EBC = ½ base x height (slant) Also, AREA of ∆EAD = 4√ 281 SA = Area of faces + Area of the base

To calculate AREA OF TRIANGULAR FACES (½ base x height) you need to know their SLANT HEIGHTS! AREA of the base □ DCBA = DC x CB SA = Area of faces + Area of the base SA = 5(√ 272) + 54(√ 281) + 80 = 379. 0286 ≈ 379 ft 2

POWERPOINT PRACTICE PROBLEM A right rectangular pyramid has base dimensions 4 m by 6 m, and a height of 8 m. Calculate the surface area of the pyramid to the nearest square metre.

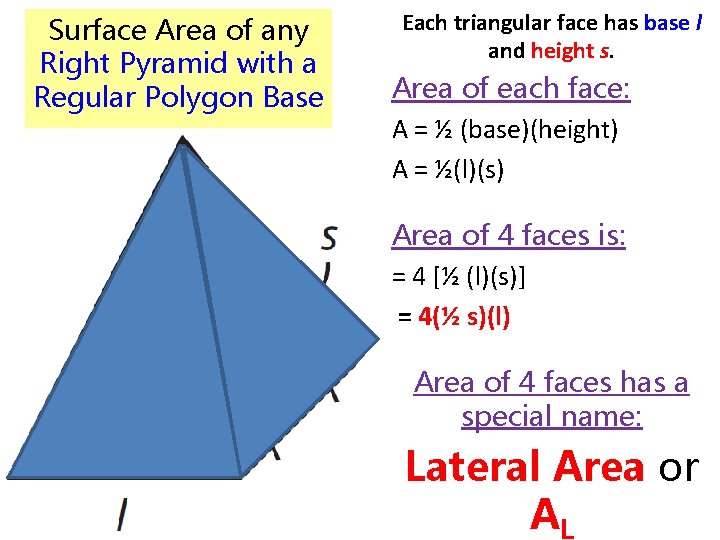
Surface Area of any Right Pyramid with a Regular Polygon Base

Surface Area of any Right Pyramid with a Regular Polygon Base Each triangular face has base l and height s. Area of each face: A = ½ (base)(height) A = ½(l)(s) Area of 4 faces is: = 4 [½ (l)(s)] = 4(½ s)(l) Area of 4 faces has a special name: Lateral Area or AL

Surface Area of any Right Pyramid with a Regular Polygon Base AL = 4(½ s)(l) = (½ s)(4 l) • (4 l) is a perimeter of the base So, SA of any pyramid with a polygon base: SA = Lateral Area + Area of base = AL + Area of base = (½ s)(perimeter of base) + Area of base

Right Circular Cone • is a 3 -dimensional (3 -D) object that has a circular base and a curved surface. • MUST know the vocabulary! • Height = the perpendicular distance from the apex to the base • Slant height = the shortest distance on the curved surface between the apex and a point on the circumference of the base

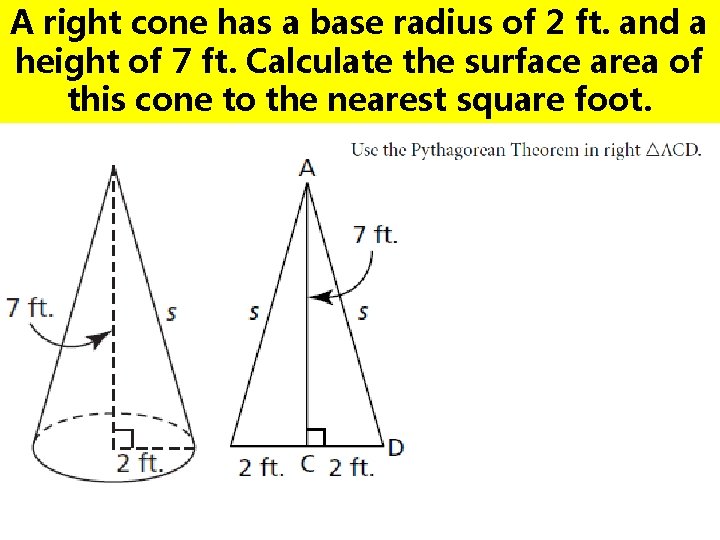
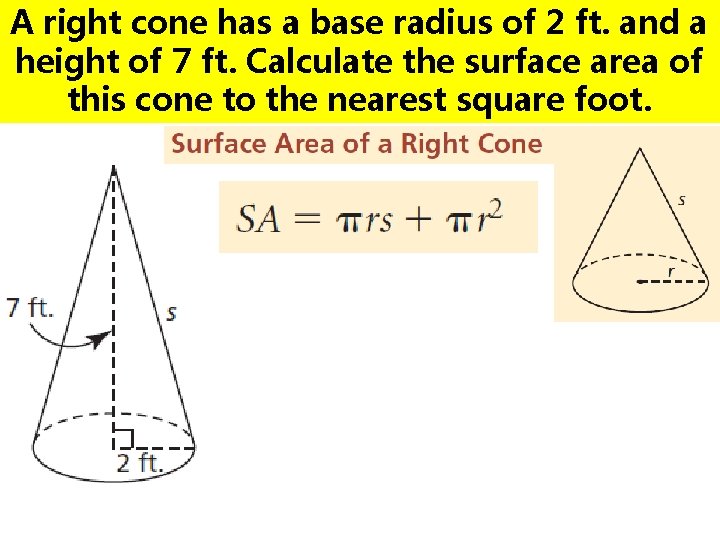
A right cone has a base radius of 2 ft. and a height of 7 ft. Calculate the surface area of this cone to the nearest square foot.

A right cone has a base radius of 2 ft. and a height of 7 ft. Calculate the surface area of this cone to the nearest square foot.

POWERPOINT PRACTICE PROBLEM A right cone has a base radius of 4 m and a height of 10 m. Calculate the surface area of this cone to the nearest square metre.

HOMEWORK �PAGE: 34 - 35 �PROBLEMS: 4, 6, 8, 9, 10, 11, 18