Review Session 1 Types of graphs SOCS 1

Review Session 1 Types of graphs, SOCS

1 of 10 Histogram • Similar to bar graph, but quantitative, and bars (usually) touch • Good for larger data sets • Break values into classes • Break up range (max-min), use judgment on # • Display count (“frequency”) in each class

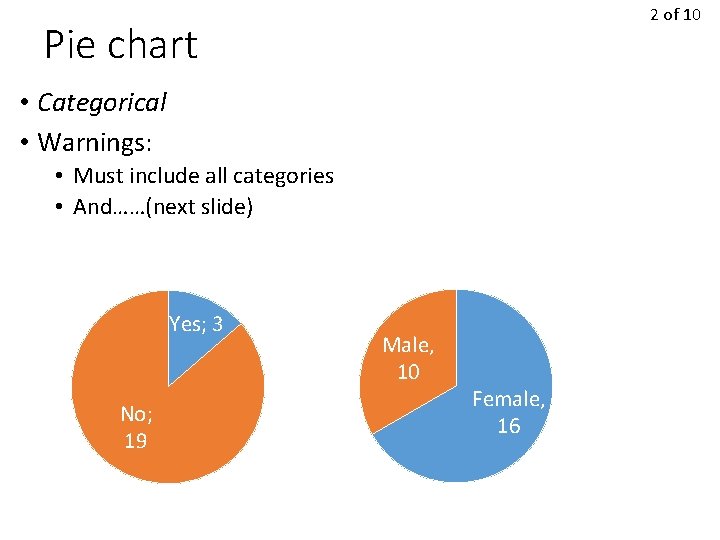
2 of 10 Pie chart • Categorical • Warnings: • Must include all categories • And……(next slide) Yes; 3 No; 19 Male, 10 Female, 16

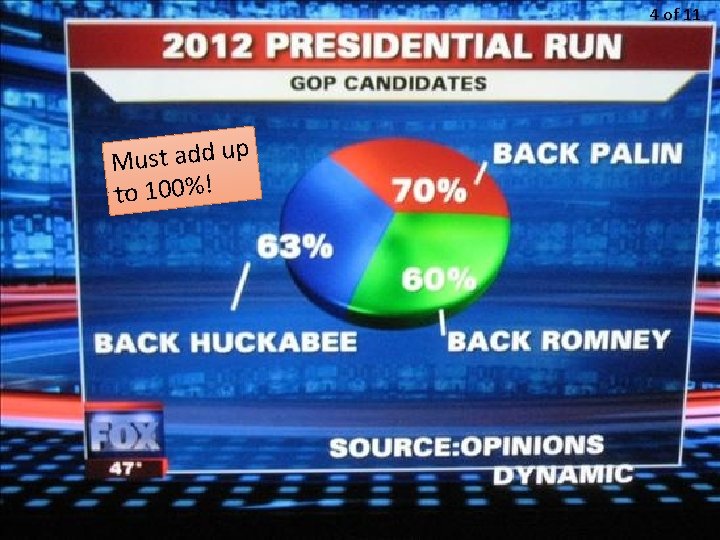
4 of 11 p Must add u to 100%!

4 of 10 Stemplot (“stem-and-leaf”) Quantitative 1. Separate into stems (usually all but last digit) and a leaf (usually last digit) 2. Stems in vertical column, consecutive. 3. Vertical line. Each leaf matches, consecutive.

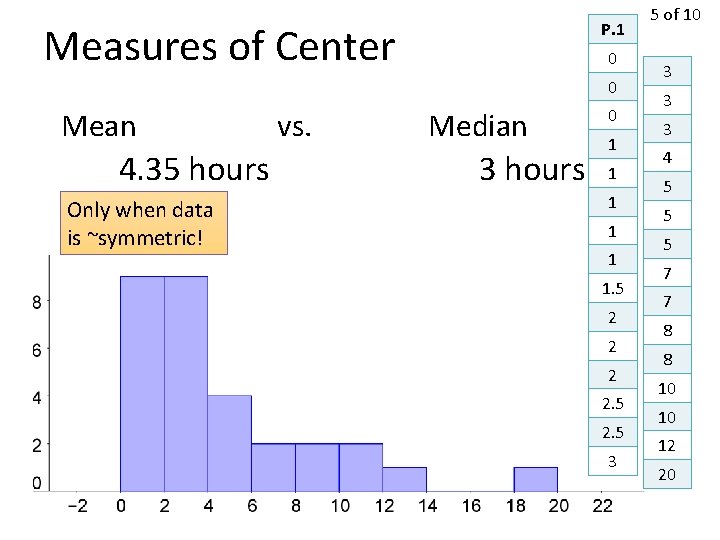
P. 1 Measures of Center 0 0 Mean 4. 35 hours Only when data is ~symmetric! vs. Median 3 hours 0 1 1 1. 5 2 2. 5 3 5 of 10 3 3 3 4 5 5 5 7 7 8 8 10 10 12 20

5 -number summary P. 2 2 0 2 0 2 • Median • Third quartile 0 3 0 3 • Maximum 0 3 0 3. 5 1 4 • Minimum • First quartile “Interquartile range” n = 30 n 6=of 2810 “Ran ge” (25 th percentile) (75 th percentile) 1. 5 x IQR Rule for Outliers An observation is an outlier if it falls more than (1. 5 x. IQR) above Q 3 or below Q 1 - (1. 5 x. IQR) Q 3 + (1. 5 x. IQR) Min 0 Q 1 0 Med 2 1 5 Q 3 3 1 5 2 8 2 9 Max 59

Standard Deviation 7 of 10 P. 2 0 • Average distance from mean. 0 • Only use when the mean is chosen as the measure of center • Sensitive to outliers 2. 25 0 – Average of the squares of the “deviations” from the mean or 1. 54 0 0 0 2 2 3 3 3 1 3. 5 1 4 1 2 2 2 5 5 8

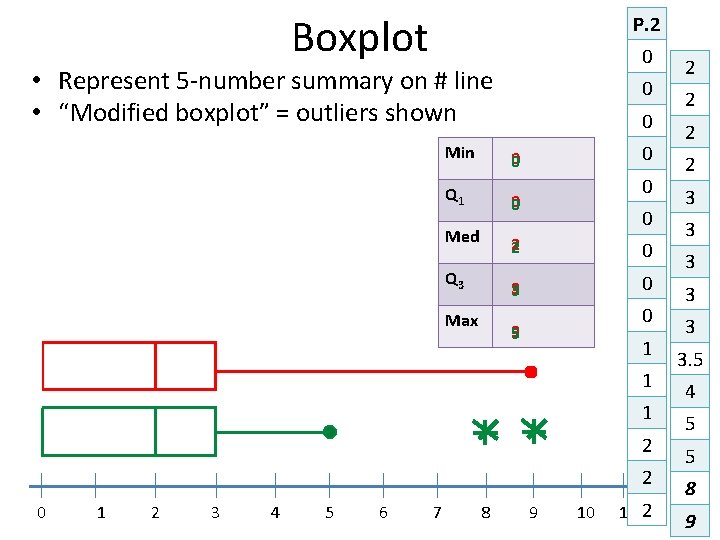
Boxplot P. 2 0 • Represent 5 -number summary on # line • “Modified boxplot” = outliers shown 0 0 0 Min 0 Q 1 0 Med 2 0 3 0 Q 3 Max 0 0 0 9 5 1 1 1 2 2 0 1 2 3 4 5 6 7 8 9 10 11 2 2 2 3 3 3. 5 4 5 5 8 9

9 of 10 Types of graphs Quantitative Categorical • Histogram (Good for large • Bar graph • Pie chart data sets) • Dotplot • Stemplot • Boxplot (Modified good for outliers)

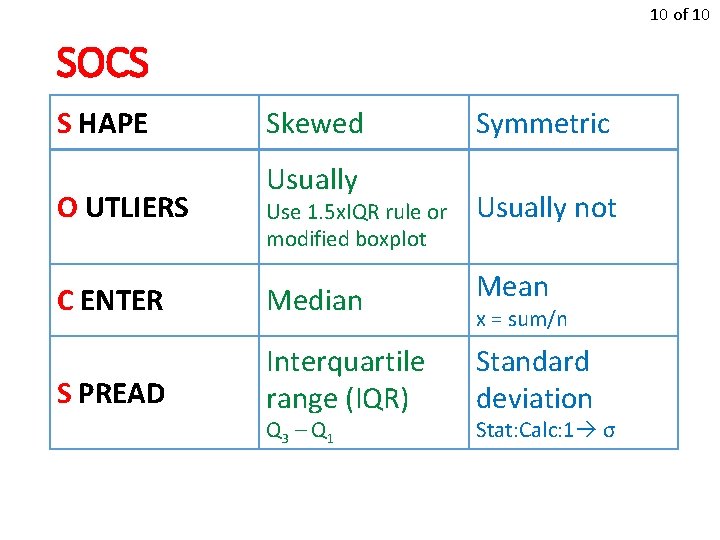
10 of 10 SOCS S HAPE O UTLIERS Skewed Usually Use 1. 5 x. IQR rule or modified boxplot Symmetric Usually not C ENTER Median Mean S PREAD Interquartile range (IQR) Standard deviation Q 3 – Q 1 x = sum/n Stat: Calc: 1 σ