Review scheme language things that make up scheme

Review: scheme language • things that make up scheme programs: • self-evaluating 23, "hello", #t • names +, pi • combinations (+ 2 3) (* pi 4) • special forms (define pi 3. 14) • syntax • combination: (oper-expression other-expressions …) • special form: special keyword as first subexpression • semantics • combinations: evaluate subexpressions in any order apply operator to operands • special forms: each one special מבוא מורחב 1

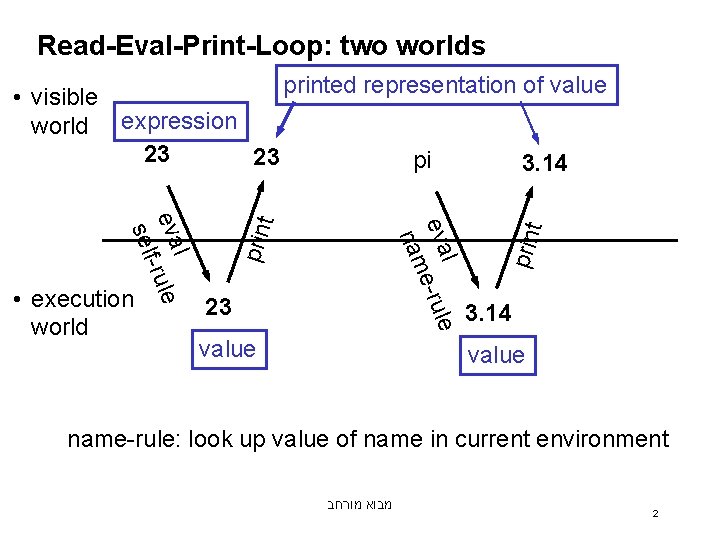
Read-Eval-Print-Loop: two worlds 23 value t prin l eva e-rule nam l eva -rule self • execution world t printed representation of value • visible world expression 23 23 pi 3. 14 value name-rule: look up value of name in current environment מבוא מורחב 2

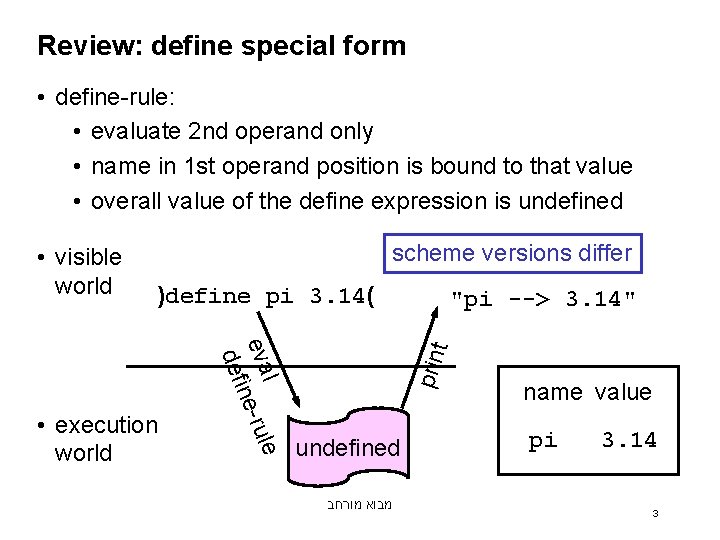
Review: define special form • define-rule: • evaluate 2 nd operand only • name in 1 st operand position is bound to that value • overall value of the define expression is undefined scheme versions differ )define pi 3. 14( t l e eva ne-rul i def • execution world "pi --> 3. 14" prin • visible world undefined מבוא מורחב name value pi 3. 14 3

Mathematical operators are just names 8 <==(5 3 +). 1 ). 2 define fred +) ==> undef ). 3 fred 4 6) ==> 10 • How to explain this? • Explanation: • + is just a name • + is bound to a value which is a procedure • line 2 binds the name fred to that same value מבוא מורחב 4

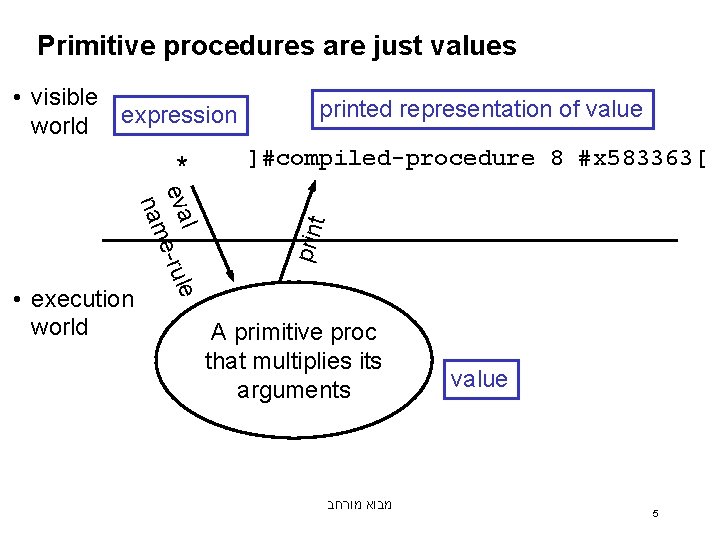
Primitive procedures are just values • visible world expression t l eva e-rule nam • execution world ]#compiled-procedure 8 #x 583363[ prin * printed representation of value A primitive proc that multiplies its arguments מבוא מורחב value 5

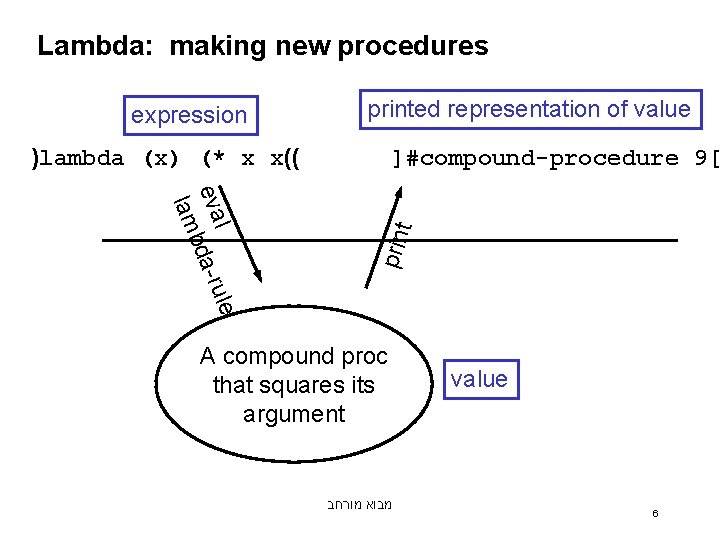
Lambda: making new procedures expression printed representation of value )lambda (x) (* x x(( prin l l eva bda-ru lam t ]#compound-procedure 9[ e A compound proc that squares its argument מבוא מורחב value 6

Interaction of define and lambda ). 1 ). 2 ). 3 )). 4 lambda (x) (* x x)) ==> #[compound-procedure 9[ define square (lambda (x) (* x x))) ==> undef square 4) ==> 16 lambda (x) (* x x)) 4) ==> 16 Syntactic Sugar: 5. (define (square x) (* x x)) ==> undef • a convenient shorthand for 2 above • this is a use of lambda! 7

Lambda special form • lambda syntax (lambda (x y) (/ (+ x y) 2)) • 1 st operand position: the parameter list (x y) • a list of names (perhaps empty) • determines the number of operands required • 2 nd operand position: the body (/ (+ x y) 2) • may be any expression • not evaluated when the lambda is evaluated • evaluated when the procedure is applied • semantics of lambda: מבוא מורחב 8

THE VALUE OF A LAMBDA EXPRESSION IS A PROCEDURE מבוא מורחב 9

Your turn: fill in each box • )define twice( )lambda (x) (* 2 x(( • )twice 2) ==> 4 (twice 3) ==> 6 • )define constant 2 (lambda () 2(( • 2 <== )constant 2( • )define second )lambda (x y z) y( ) • (second 2 15 3) ==> 15 (second 34 -5 16) ==> -5 מבוא מורחב 10

Substitution model • a way to figure out what happens during evaluation • not really what happens in the computer • to apply a compound procedure: evaluate the body of the procedure, with each parameter replaced by the corresponding operand • to apply a primitive procedure: just do it (define square (lambda (x) (* x x))) 1. 2. 3. (square 4) (* 4 4) 16 מבוא מורחב 11

Substitution model details )define square (lambda (x) (* x x))) (define average (lambda (x y) (/ (+ x y) 2((( )average 5 (square 3)) (average 5 (* 3 3)) (average 5 9) first evaluate operands, then substitute (applicative order) (/ (+ 5 9) 2) (/ 14 2) 7 if operator is a primitive procedure, replace by result of operation מבוא מורחב 12

A less trivial procedure: sum of squares • S(n) = 02 + 12 + 22 ………. …… + n 2 • Notice that S(n) = S(n-1) + n 2 • Also notice that S(0) = 0 (define sum-sq (lambda (n) (if (= n 0) 0 (+ (sum-sq (- n 1)) (square n)))) • predicate = tests numerical equality (= 4 4) ==> #t (true) (= 4 5) ==> #f (false) • if special form (if (= 4 4) 2 3) ==> 2 (if (= 4 5) 2 3) ==> 3 predicate consequent alternative 13

IF special form (if <predicate> <consequent> <alternative>) • When the value of <predicate> is #f, the value of the expression is the value of <alternative>. Otherwise it is the value of <consequent> (if (< 2 3) 1 (/ 1 0)) ==> 1 (if (< 3 2) 0 (> 9 8 7)) ==> # t מבוא מורחב 14

)define (sum-sq n) (if (= n 0) 0 (+ (sum-sq (- n 1)) (square n(((( )sum-sq 3( (if (= 3 0) 0 (+ (sum-sq (- 3 1)) (square 3))) (if #f 0 (+ (sum-sq (- 3 1)) (square 3))) (+ (sum-sq (- 3 1)) (square 3)) (+ (sum-sq (- 3 1)) (* 3 3)) (+ (sum-sq (- 3 1)) 9) (+ (sum-sq 2) 9) (+ (if (= 2 0) 0 (+ (sum-sq (- 2 1)) (square 2))) 9) . . (+ (+ (sum-sq 1) 4) 9) . . (+ (+ (+ (sum-sq 0) 1) 4) 9) (+ (+ (+ (if (= 0 0) 0(+ (sum-sq (- 0 1)) (square 0))) 1) 4) 9) . . (+ (+ (+ 0 1) 4) 9) . . 14 מבוא מורחב 15

How to design recursive algorithms • follow the general pattern: 1. wishful thinking 2. decompose the problem 3. identify non-decomposable (smallest) problems 1. Wishful thinking • Assume the desired procedure exists. • want to implement sum-sq ? OK, assume it exists. • BUT, only solves a smaller version of the problem. מבוא מורחב 16

2. Decompose the problem • Solve a problem by 1. solve a smaller instance (using wishful thinking) 2. convert that solution to the desired solution • Step 2 requires creativity! • Must design the strategy before coding. • S(n) = S(n-1) + n 2 • solve the smaller instance, add n 2 to get the solution (define sum-sq (lambda (n) (+ (sum-sq(- n 1)) (square n)))) מבוא מורחב 17

3. Identify non-decomposable problems • Decomposing not enough by itself • Must identify the "smallest" problems and solve directly • S(0)=0 (define sum-sq (lambda (n) (if (= n 0) 0 (+ (sum-sq (- n 1)) (square n))))) מבוא מורחב 18

General form of recursive algorithms • test, base case, recursive case (define sum-sq (lambda (n) (if (= n 0) ; test for base case 0 ; base case (+ (sum-sq (- n 1)) (square n)) ; recursive case ))) • base case: smallest (non-decomposable) problem • recursive case: larger (decomposable) problem מבוא מורחב 19

Another example • odd? (define odd? (lambda (n) (if (= n 0) #f ; test for base case ; base case (not (odd? (- n 1))) ; recursive case ))) • See another way to write it in the notes מבוא מורחב 20

Short summary • Design a recursive algorithm by 1. wishful thinking 2. decompose the problem 3. identify non-decomposable (smallest) problems • Recursive algorithms have 1. test 2. recursive case 3. base case מבוא מורחב 21

Procedural abstraction • Abstractions hide complexity • Several fundamental kinds of abstraction this term • Procedural abstraction is one: • (sum-sq n) computes S(n) • user doesn't have to think about the internals מבוא מורחב 22

Procedural abstraction (sqrt) To find an approximation of square root of x: • Make a guess G • Improve the guess by averaging G and x/G • Keep improving the guess until it is good enough X=2 G=1 X/G = 2 G = ½ (1+ 2) = 1. 5 X/G = 4/3 G = ½ (3/2 + 4/3) = 17/12 = 1. 416666 X/G = 24/17 G = ½ (17/12 + 24/17) = 577/408 = 1. 4142156 מבוא מורחב 23

)define (sqrt x( ) sqrt-iter 1. 0 x(( (define (sqrt-iter guess x) (if (good-enough? guess x) guess (sqrt-iter (improve guess x) x))) (define (good-enough? guess x) (< (abs (- (square guess) x)) 0. 001)) (define (improve guess x) (average guess (/ x guess))) מבוא מורחב 24

Block Structure )define (sqrt x( ) define (good-enough? guess x( ) >) abs (- (square guess) x)) 0. 001(( ) define (improve guess x( ) average guess (/ x guess((( ) define (sqrt-iter guess x( ) if (good-enough? guess x( guess ) sqrt-iter (improve guess x) x((( ) sqrt-iter 1. 0 x(( מבוא מורחב 25

Lexical Scoping )define (sqrt x( ) define (good-enough? guess( ) >) abs (- (square guess) x)) 0. 001(( ) define (improve guess( ) average guess (/ x guess((( ) define (sqrt-iter guess( ) if (good-enough? guess( guess ) sqrt-iter (improve guess(((( ) sqrt-iter 1. 0(( מבוא מורחב 26

) <=sqrt 4( ) define (good-enough? guess( ) >) abs (- (square guess) 4)) 0. 001(( ) define (improve guess( ) average guess (/ 4 guess((( ) define (sqrt-iter guess( ) if (good-enough? guess( guess ) sqrt-iter (improve guess(((( ) sqrt-iter 1. 0( (if (good-enough? 1. 0) 1. 0 (sqrt-iter (improve 1. 0))) מבוא מורחב 27

)define (h ) define ) g (* 2 ) <=h x( (f y) (+ x y(( (g x) (f x((( 1( (define (f y) (define (g x) (g (* 2 1)) (f (+ 3 (+ 1 y)) (f x)) 2) 1 2) מבוא מורחב 28