Review Quick Sort Algorithm Time Complexity Best case

Review �Quick Sort Algorithm �Time Complexity �Best case �Average case �Worst case �Examples 1

Quick Sort Example 2

Merge Sort �Merge Sort Algorithm �Time Complexity �Best case �Average case �Worst case �Examples 3

Introduction �Merging is the process of combining two or more sorted array into a third sorted array � Apply divide-and-conquer to sorting problem � Divide the array into approximately n/2 sub-arrays of size two and sort the elements in each sub array � Merging each sub-array with the adjacent sub-array will get another sorted sub-array � Repeat this process until there is only one array remaining of size n � Since at any time the two arrays being merged are both sub-arrays of A, lower and upper bounds are required to indicate the sub-arrays being merged 4

�Let A be an array of n number of elements to be 5 sorted A[1], A[2]. . . A[n] �Step 1: Divide the array A into approximately n/2 sorted sub-array, i. e. , the elements in the (A [1], A [2]), (A [3], A [4]), (A [k], A [k + 1]), (A [n – 1], A [n]) sub-arrays are in sorted order �Step 2: Merge each pair of pairs to obtain the following list of sorted sub-array �The elements in the sub-array are also in the sorted order �(A [1], A [2], A [3], A [4)), . . . (A [k – 1], A [k + 2]), . . . (A [n – 3], A [n – 2], A [n – 1], A [n]). �Step 3: Repeat the step 2 recursively until there is

Example �To illustrate the merge sort algorithm consider the following array with 7 elements �[42], [33], [23], [74], [44], [67], [49] 6
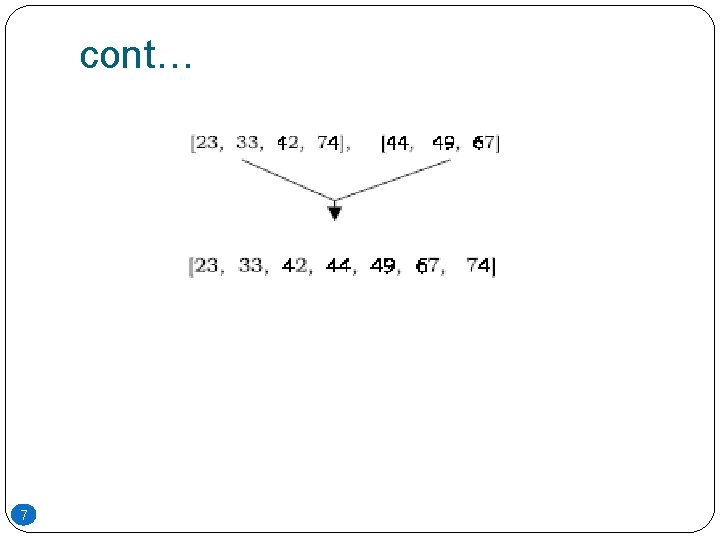
cont… 7

Merging �The key to Merge Sort is merging two sorted lists into one, such that if you have two lists X (x 1 x 2 … xm) and Y(y 1 y 2 … yn) the resulting list is Z(z 1 z 2 … zm+n) �Example: L 1 = { 3 8 9 } L 2 = { 1 5 7 } merge(L 1, L 2) = { 1 3 5 7 8 9 } 8
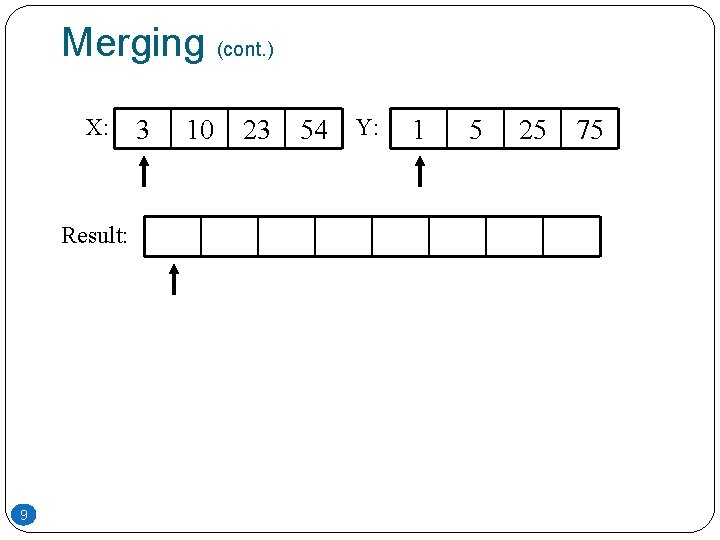
Merging (cont. ) X: Result: 9 3 10 23 54 Y: 1 5 25 75
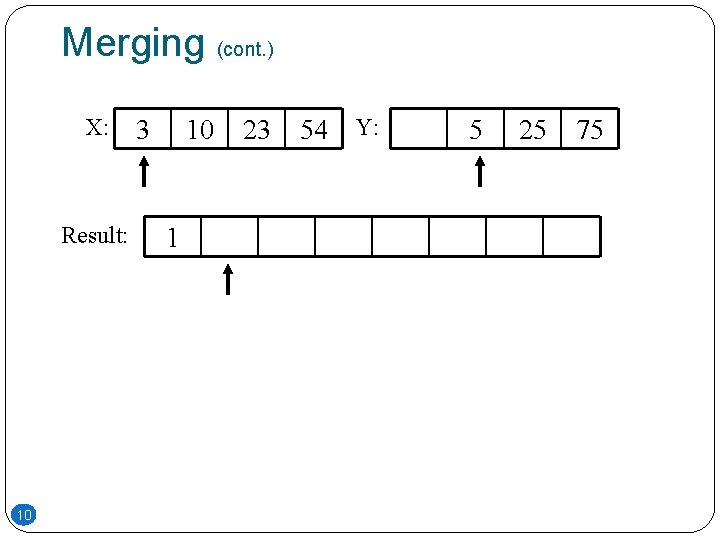
Merging (cont. ) X: Result: 10 3 10 1 23 54 Y: 5 25 75
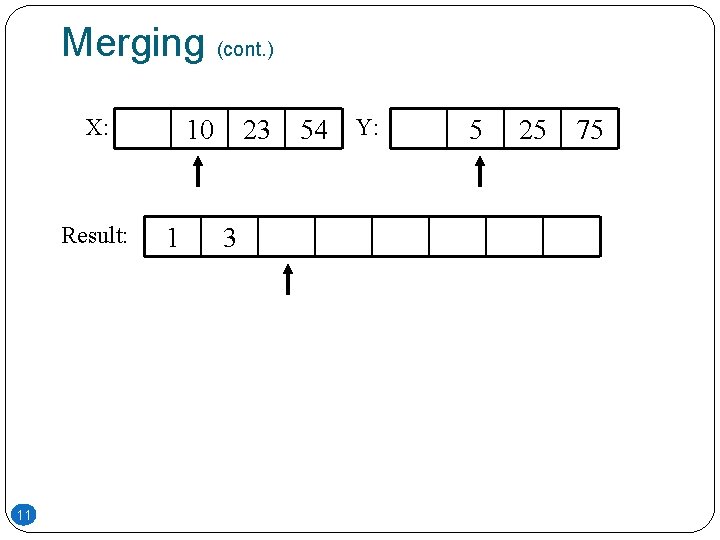
Merging (cont. ) X: Result: 11 10 1 23 3 54 Y: 5 25 75
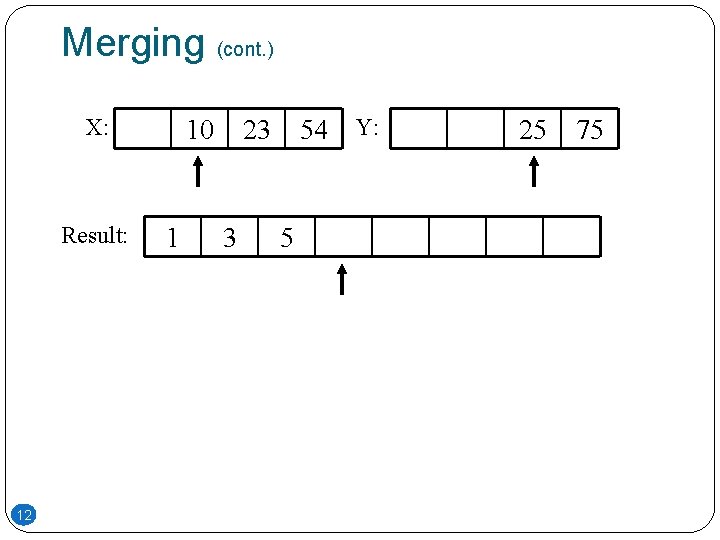
Merging (cont. ) X: Result: 12 10 1 54 Y: 23 3 5 25 75
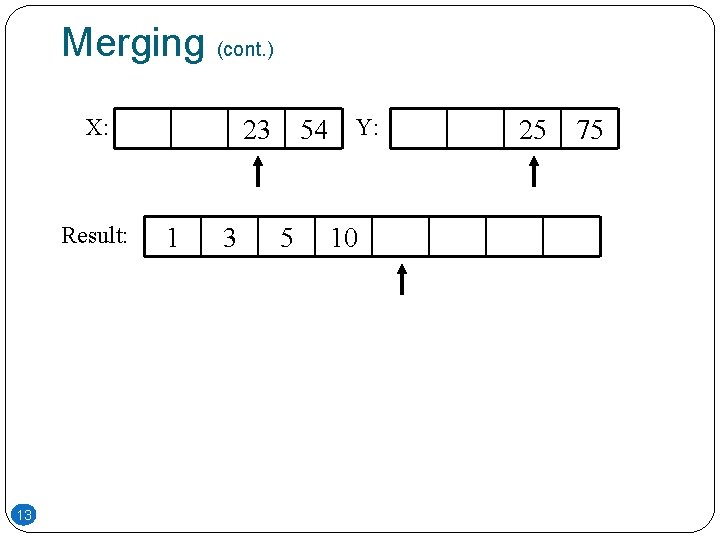
Merging (cont. ) X: Result: 13 54 Y: 23 1 3 5 10 25 75
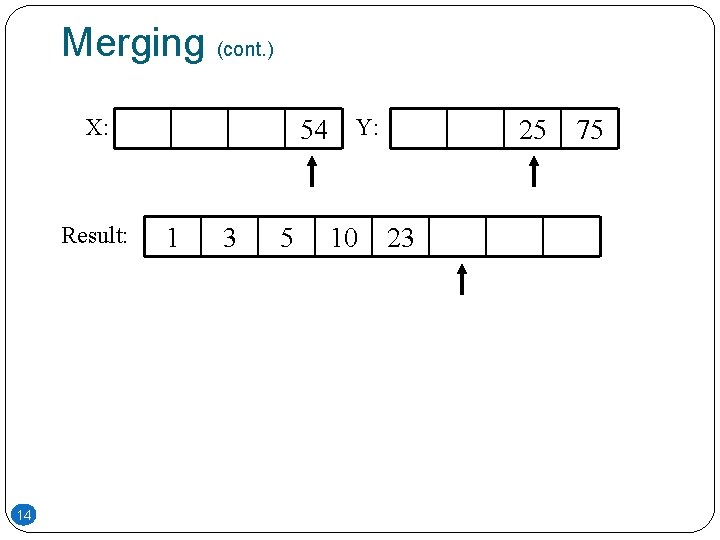
Merging (cont. ) X: Result: 14 54 Y: 1 3 5 10 25 23 75
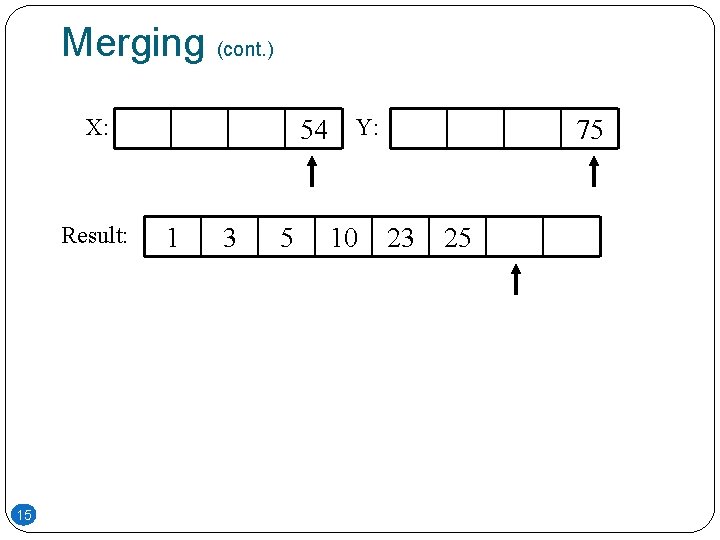
Merging (cont. ) X: Result: 15 54 Y: 1 3 5 10 75 23 25
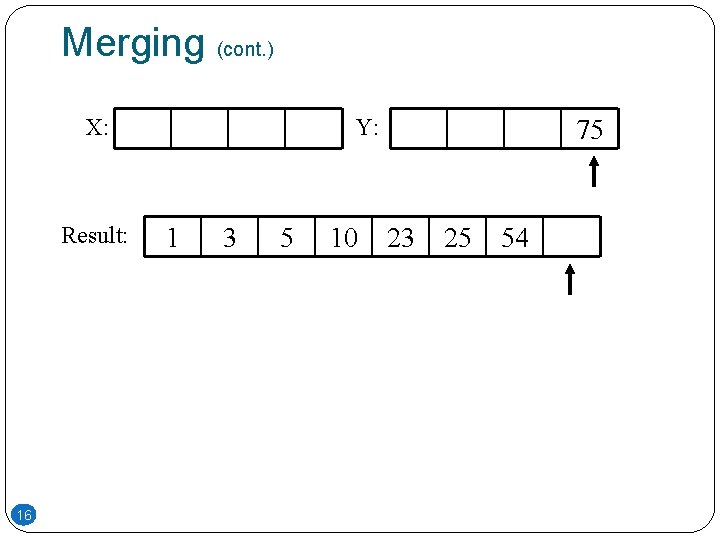
Merging (cont. ) X: Result: 16 Y: 1 3 5 10 75 23 25 54
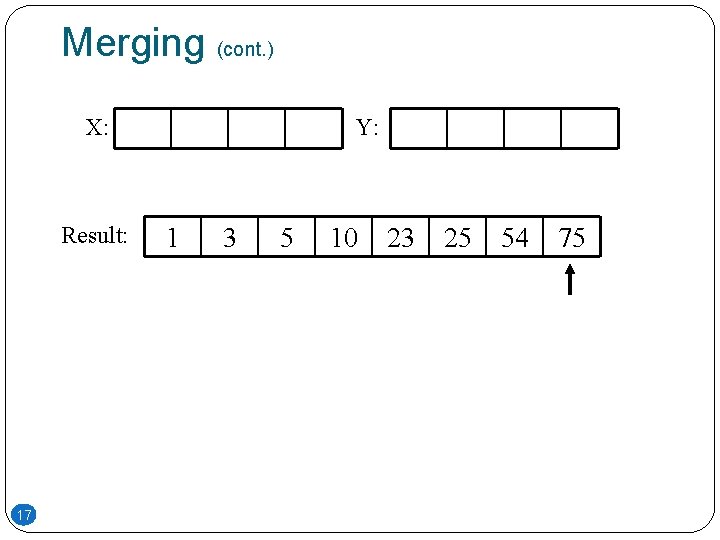
Merging (cont. ) X: Result: 17 Y: 1 3 5 10 23 25 54 75

Divide And Conquer �Merging a two lists of one element each is the same as sorting them. �Merge sort divides up an unsorted list until the above condition is met and then sorts the divided parts back together in pairs. �Specifically this can be done by recursively dividing the unsorted list in half, merge sorting the right side then the left side and then merging the right and left back together. 18

Merge Sort Algorithm Given a list L with a length k: �If k == 1 the list is sorted �Else: �Merge Sort the left side (1 thru k/2) �Merge Sort the right side (k/2+1 thru k) �Merge the right side with the left side 19

Merge Sort Example 99 20 6 86 15 58 35 86 4 0
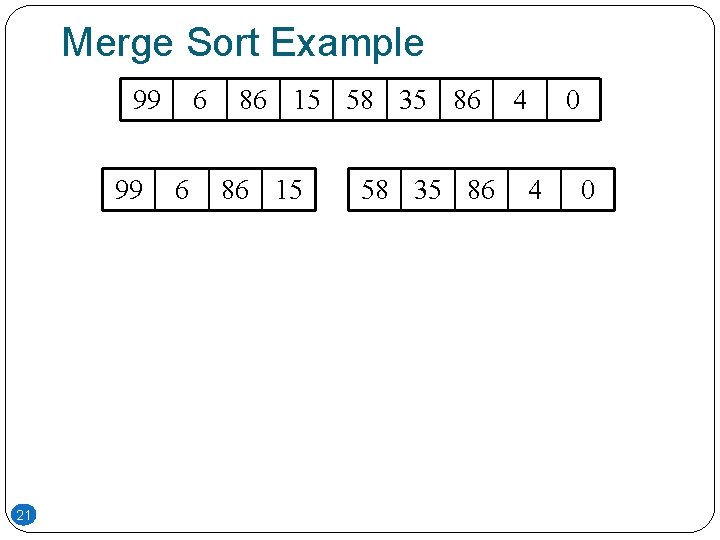
Merge Sort Example 99 99 21 6 6 86 15 58 35 86 4 0
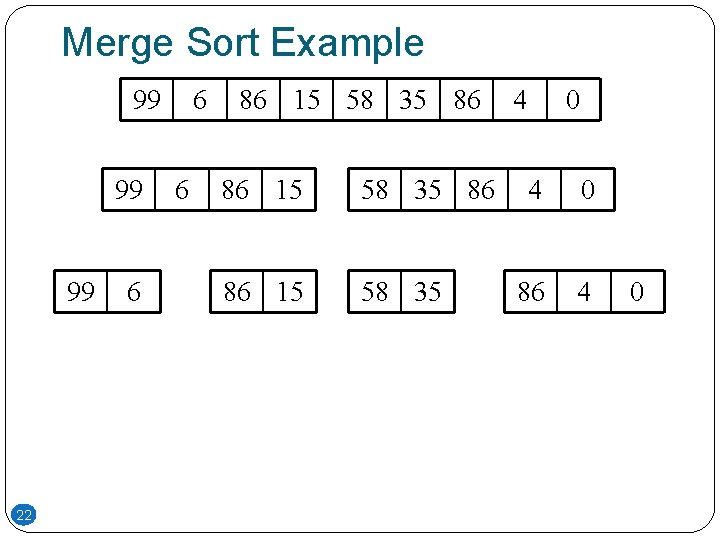
Merge Sort Example 99 99 99 22 6 6 6 86 15 58 35 86 86 15 58 35 4 0 86 4 0
Merge Sort Example 99 99 23 6 6 86 15 58 35 86 86 15 4 0 58 35 86 4 58 86 35 0 4 0
Merge Sort Example 99 99 24 6 6 86 15 58 35 86 86 15 4 0 58 35 86 4 58 86 35 0 4 4 0 0
Merge Sort Example 99 Merge 25 6 86 15 58 35 86 0 4 4 0
Merge Sort Example 6 99 Merge 26 99 6 15 86 86 15 58 35 0 58 86 35 4 86 0 4
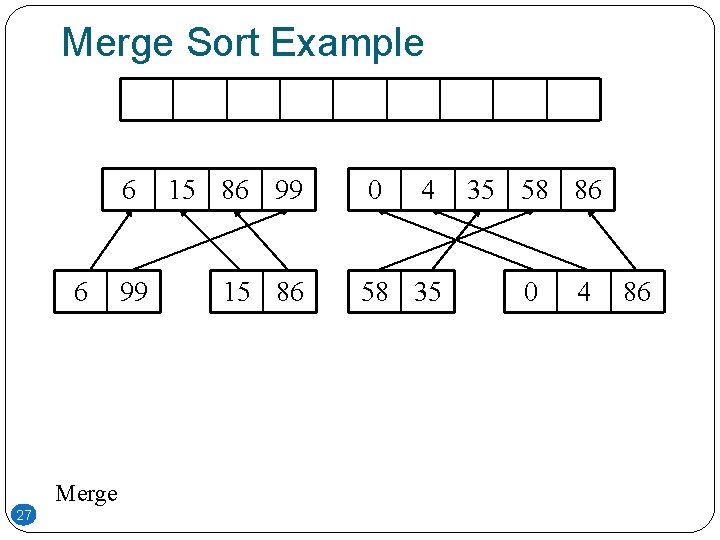
Merge Sort Example 6 6 Merge 27 99 15 86 0 4 58 35 35 58 86 0 4 86

Merge Sort Example 0 6 Merge 28 4 6 15 35 58 86 86 99 15 86 99 0 4 35 58 86

Merge Sort Example 0 29 4 6 15 35 58 86 86 99

Implementing Merge Sort � There are two basic ways to implement merge sort: �In Place: Merging is done with only the input array �Pro: Requires only the space needed to hold the array �Con: Takes longer to merge because if the next element is in the right side then all of the elements must be moved down. �Double Storage: Merging is done with a temporary array of the same size as the input array. �Pro: Faster than In Place since the temp array holds the resulting array until both left and right sides are merged into the temp array, then the temp array is appended over the input array. �Con: The memory requirement is doubled. 30

Merge Sort Analysis The Double Memory Merge Sort runs O (N log N) for all cases, because of its Divide and Conquer approach. T(N) = 2 T(N/2) + N = O(N log. N) 31

Cont… There are other variants of Merge Sorts including kway merge sorting, but the common variant is the Double Memory Merge Sort. Though the running time is O(N log. N) and runs much faster than insertion sort and bubble sort, merge sort’s large memory demands makes it not very practical for main memory sorting. 32
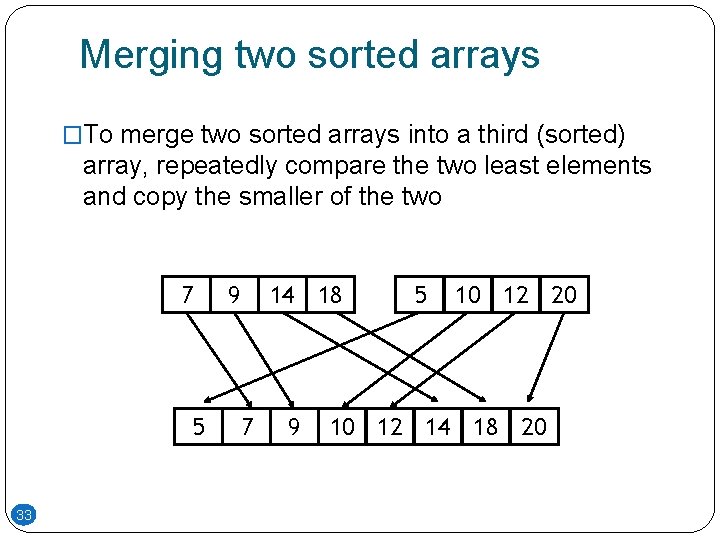
Merging two sorted arrays �To merge two sorted arrays into a third (sorted) array, repeatedly compare the two least elements and copy the smaller of the two 7 5 33 9 7 14 18 9 5 10 12 20 10 12 14 18 20
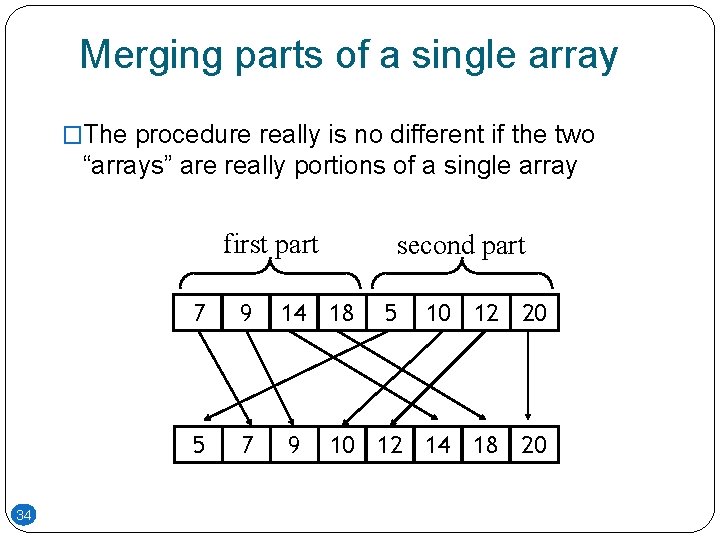
Merging parts of a single array �The procedure really is no different if the two “arrays” are really portions of a single array first part 34 second part 7 9 14 18 5 7 9 5 10 12 20 10 12 14 18 20
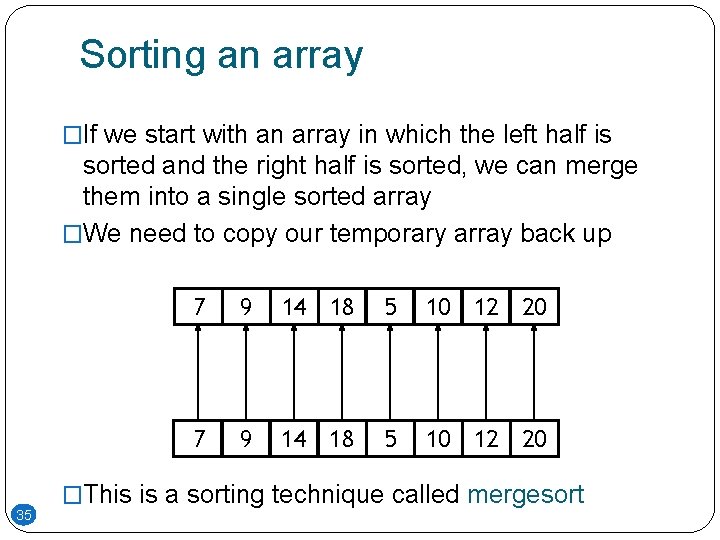
Sorting an array �If we start with an array in which the left half is sorted and the right half is sorted, we can merge them into a single sorted array �We need to copy our temporary array back up 35 7 9 14 18 5 10 12 20 �This is a sorting technique called mergesort

Recursion �How did the left and right halves of our array get sorted? �Obviously, by mergesorting them �To mergesort an array: �Mergesort the left half �Mergesort the right half �Merge the two sorted halves �Each recursive call is with a smaller portion of the array �The base case: Mergesort an array of size 1 36
![The actual code private void rec. Merge. Sort(long[] workspace, int lower. Bound, int upper. The actual code private void rec. Merge. Sort(long[] workspace, int lower. Bound, int upper.](http://slidetodoc.com/presentation_image_h2/66af25d0401ee9ea4b332a8caca8ee2c/image-37.jpg)
The actual code private void rec. Merge. Sort(long[] workspace, int lower. Bound, int upper. Bound) { if (lower. Bound == upper. Bound) return; int mid = (lower. Bound + upper. Bound) / 2; rec. Merge. Sort(workspace, lower. Bound, mid); rec. Merge. Sort(workspace, mid + 1, upper. Bound); merge(workspace, lower. Bound, mid + 1, upper. Bound); } from Lafore, p. 287 37

The merge method �The merge method is too ugly to show �It requires: �The index of the first element in the left subarray �The index of the last element in the right subarray �The index of the first element in the right subarray �That is, the dividing line between the two subarrays �The index of the next value in the left subarray �The index of the next value in the right subarray �The index of the destination in the workspace �But conceptually, it isn’t difficult! 38

Analysis of the merge operation �The basic operation is: compare two elements, move one of them to the workspace array �This takes constant time �We do this comparison n times �Hence, the whole thing takes O(n) time �Now we move the n elements back to the original array �Each move takes constant time �Hence moving all n elements takes O(n) time �Total time: O(n) + O(n) = O(n) 39
But wait. . . there’s more � So far, we’ve found that it takes O(n) time to merge two sorted halves of an array � How did these subarrays get sorted? � At the next level down, we had four subarrays, and we merged them pairwise � Since merging arrays is linear time, when we cut the 40 array size in half, we cut the time in half � But there are two arrays of size n/2 � Hence, all merges combined at the next lower level take the same amount of time as a single merge at the upper level

Analysis II �So far we have seen that it takes �O(n) time to merge two subarrays of size n/2 �O(n) time to merge four subarrays of size n/4 into two subarrays of size n/2 �O(n) time to merge eight subarrays of size n/8 into four subarrays of size n/4 �Etc. �How many levels deep do we have to proceed? �How many times can we divide an array of size n into two halves? �log 2 n, of course 41

Analysis III �So if our recursion goes log n levels deep. . . �. . . and we do O(n) work at each level. . . �. . . our total time is: log n * O(n). . . �. . . or in other words, O(n log n) �For large arrays, this is much better than Bubblesort, Selection sort, or Insertion sort, all of which are O(n 2) �Mergesort does, however, require a “workspace” array as large as our original array 42
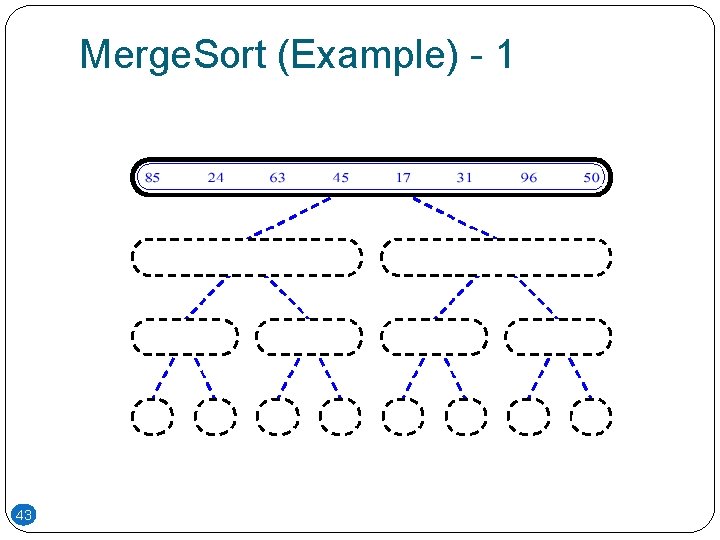
Merge. Sort (Example) - 1 43
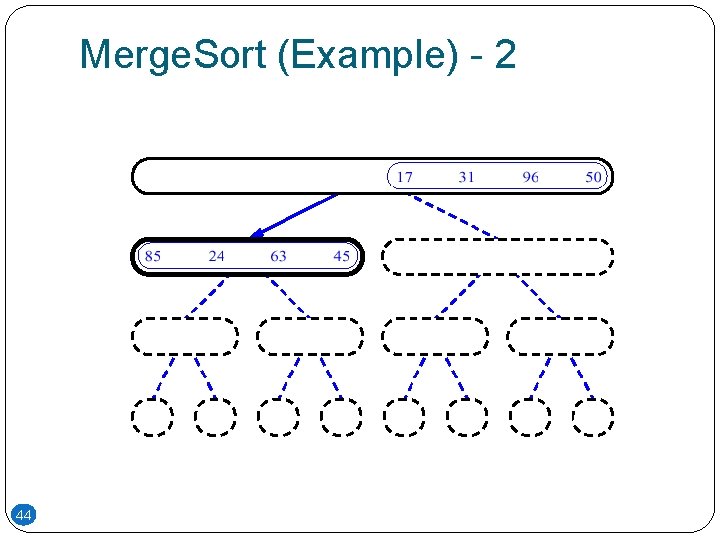
Merge. Sort (Example) - 2 44
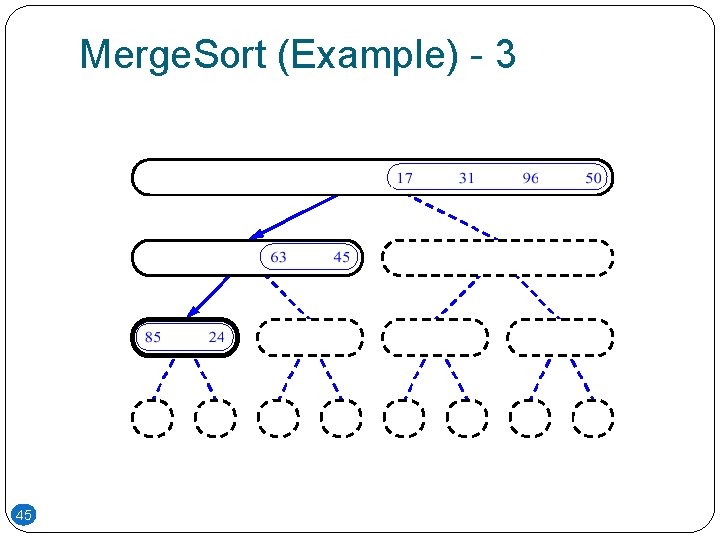
Merge. Sort (Example) - 3 45
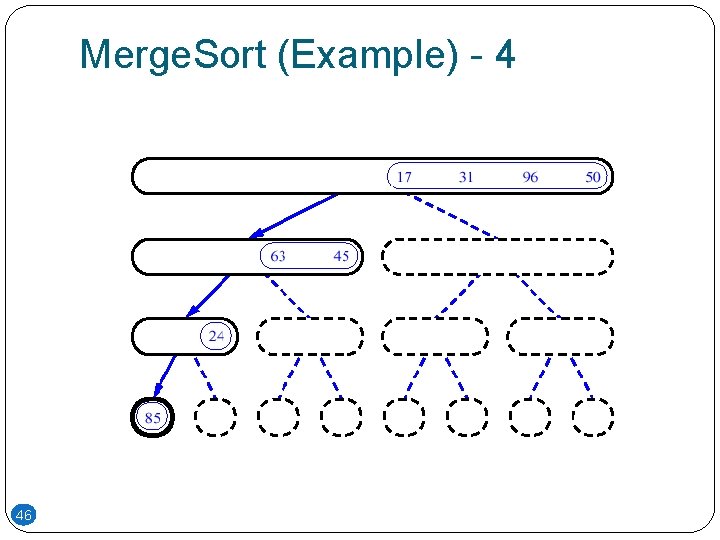
Merge. Sort (Example) - 4 46
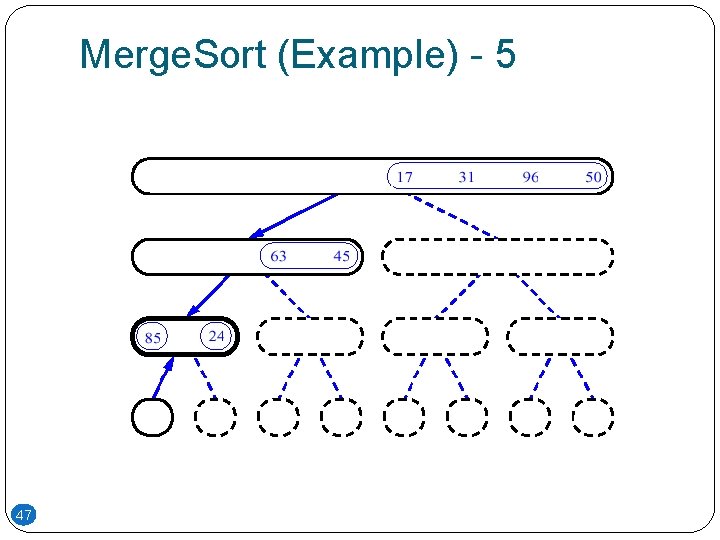
Merge. Sort (Example) - 5 47
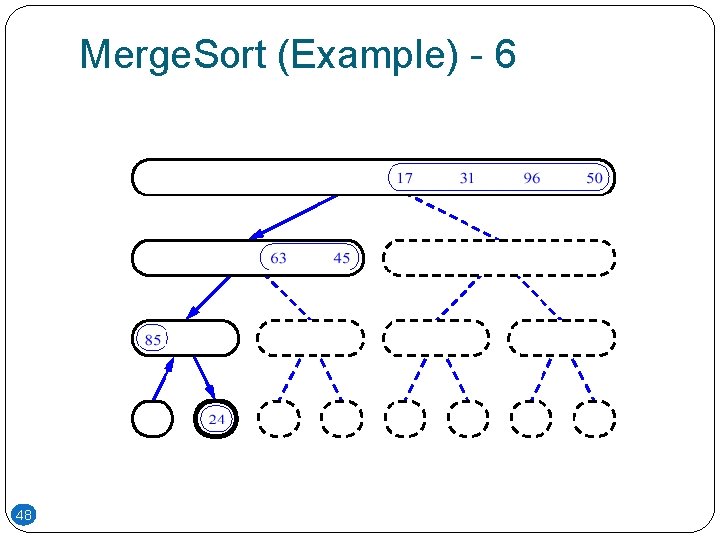
Merge. Sort (Example) - 6 48
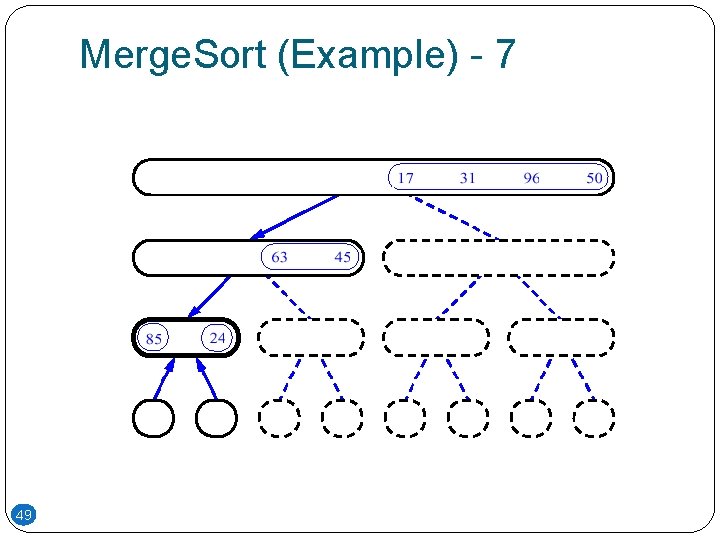
Merge. Sort (Example) - 7 49
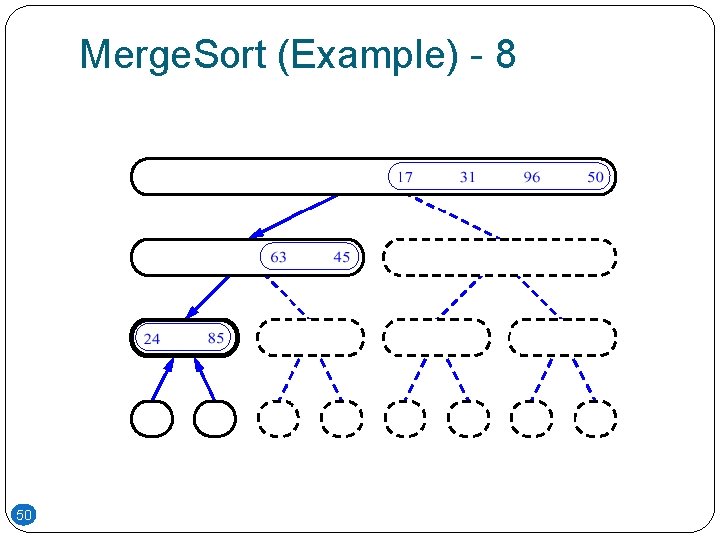
Merge. Sort (Example) - 8 50
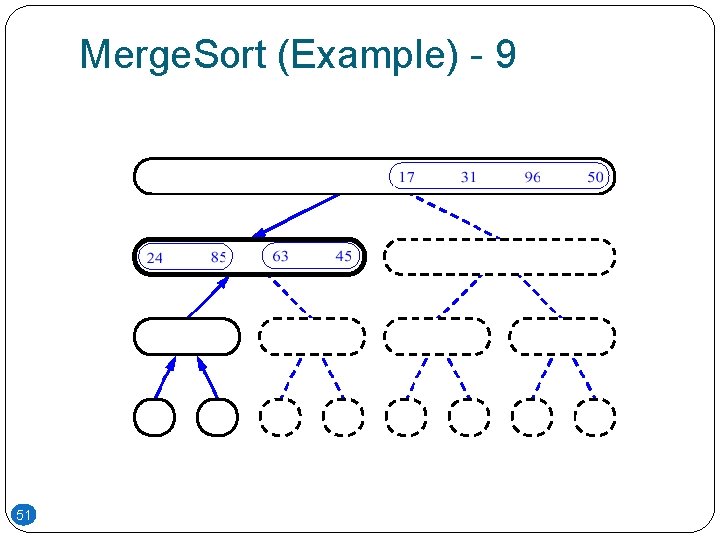
Merge. Sort (Example) - 9 51
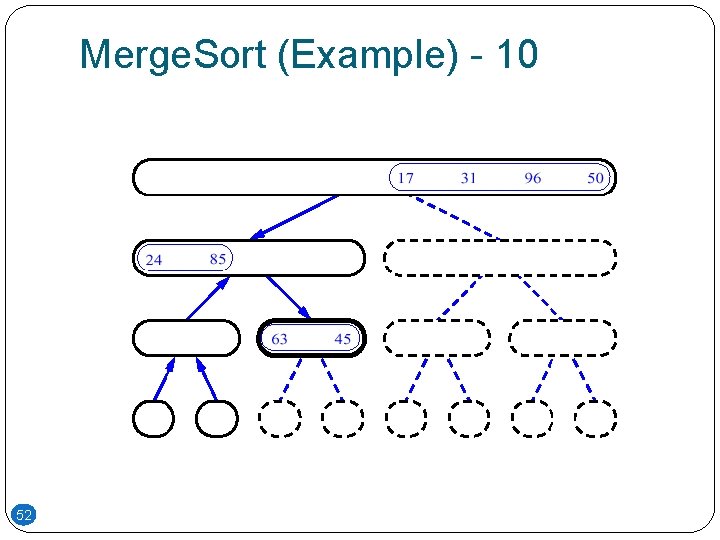
Merge. Sort (Example) - 10 52
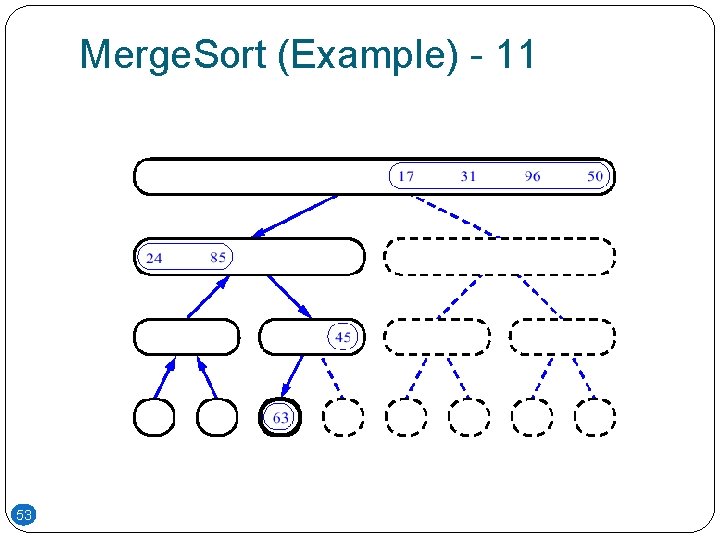
Merge. Sort (Example) - 11 53
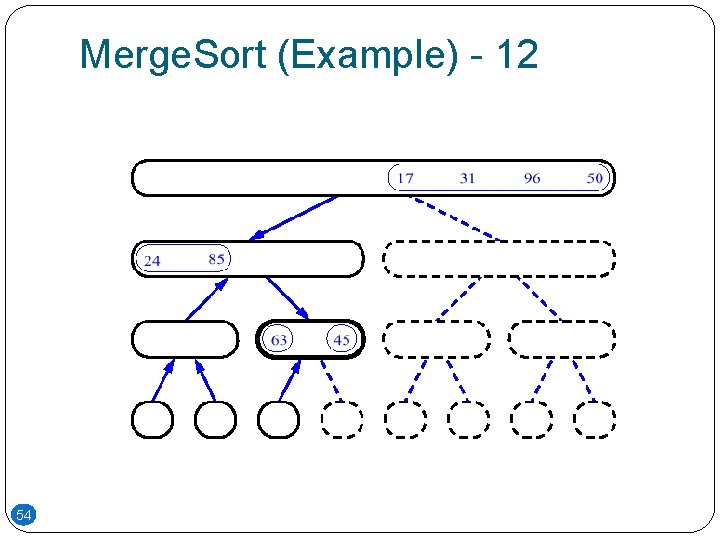
Merge. Sort (Example) - 12 54
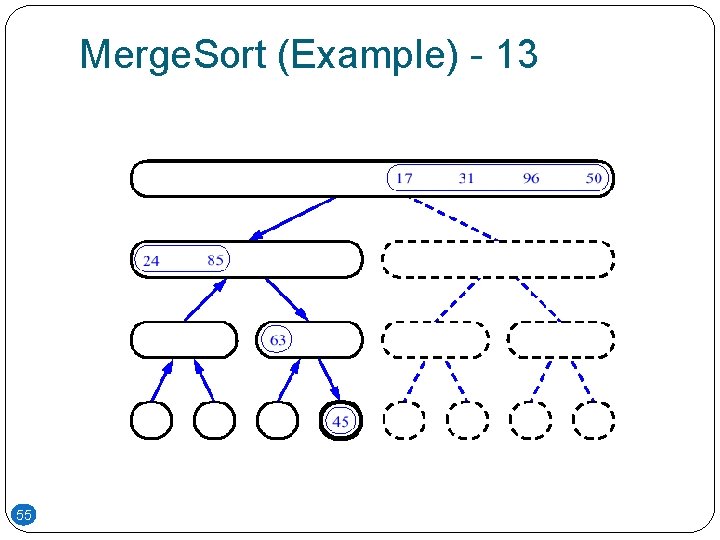
Merge. Sort (Example) - 13 55
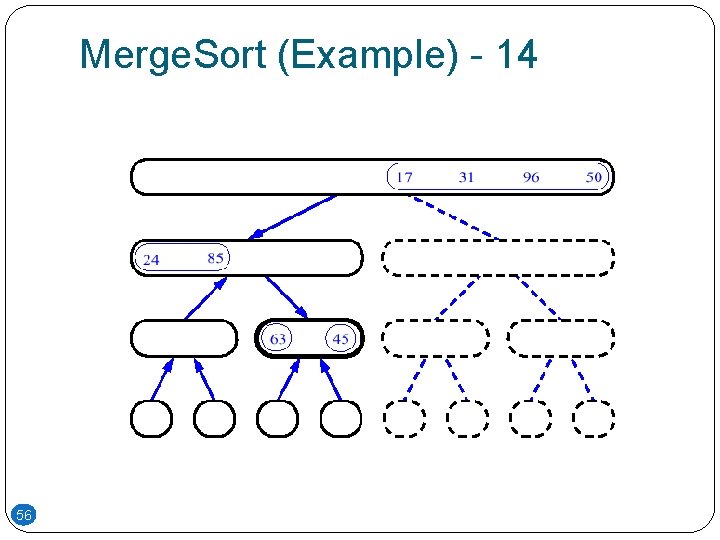
Merge. Sort (Example) - 14 56
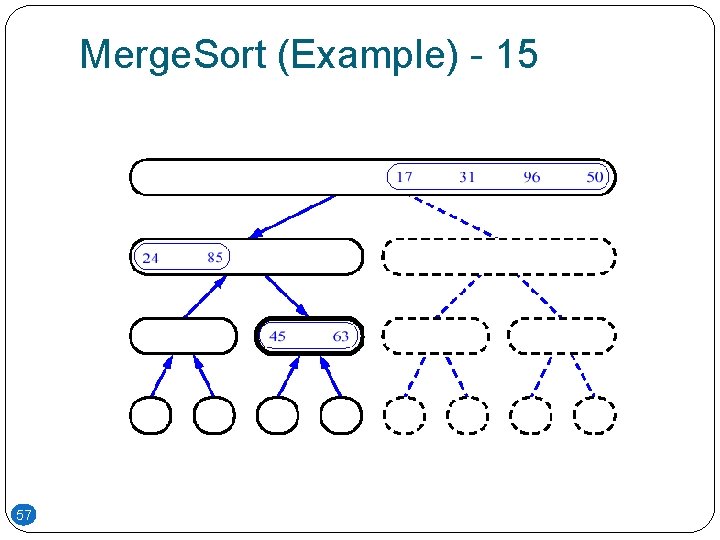
Merge. Sort (Example) - 15 57
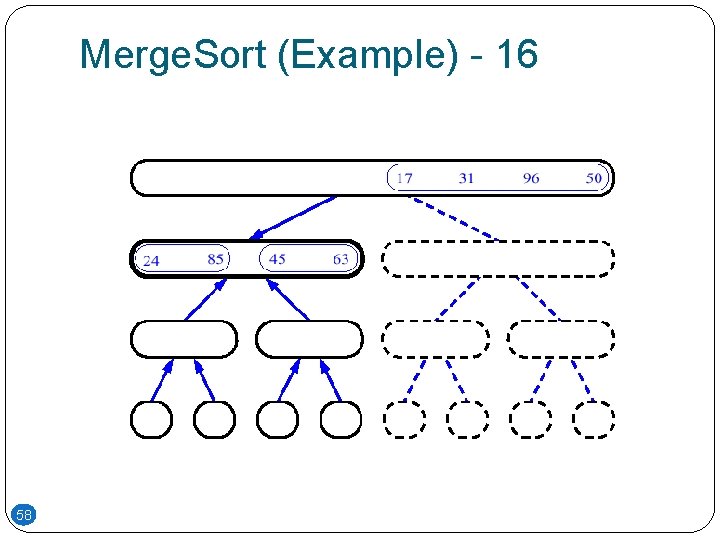
Merge. Sort (Example) - 16 58
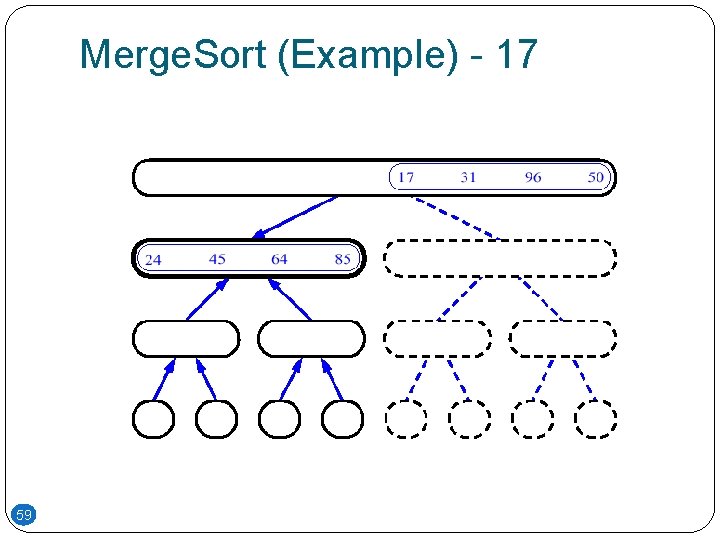
Merge. Sort (Example) - 17 59
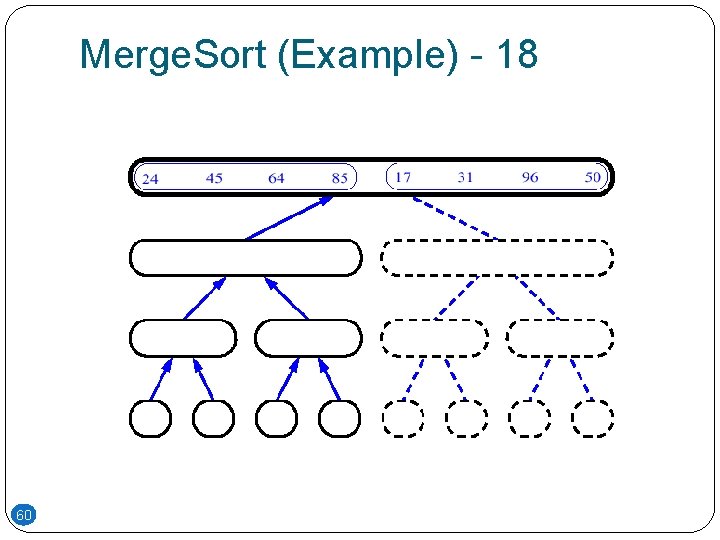
Merge. Sort (Example) - 18 60
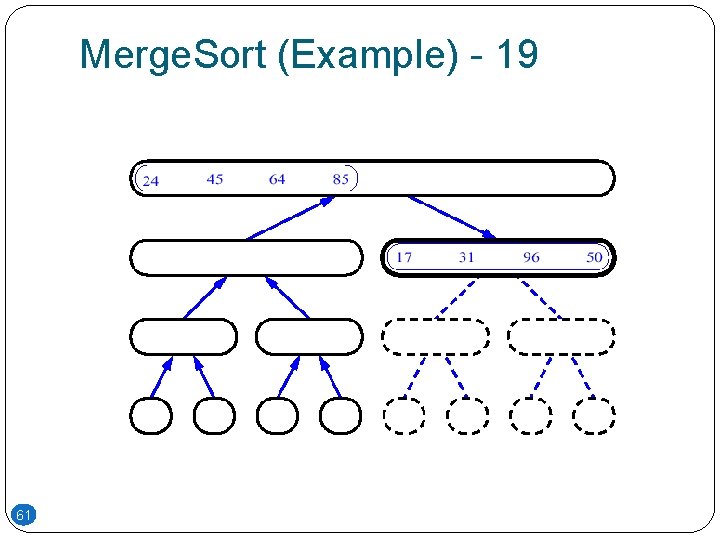
Merge. Sort (Example) - 19 61
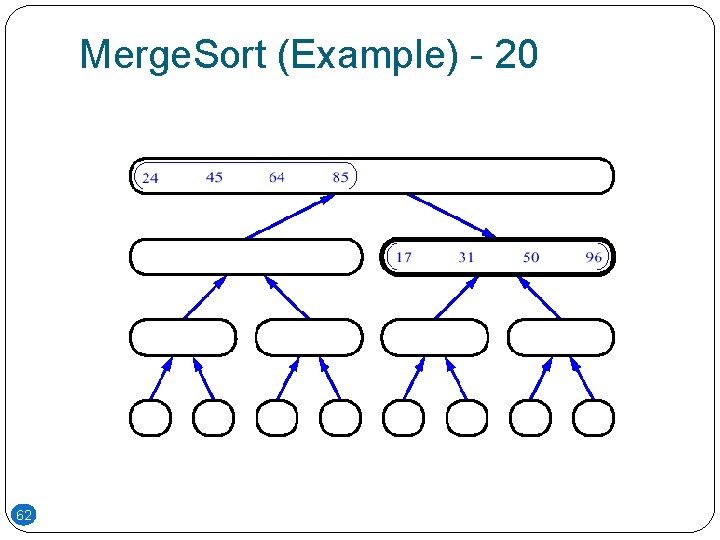
Merge. Sort (Example) - 20 62
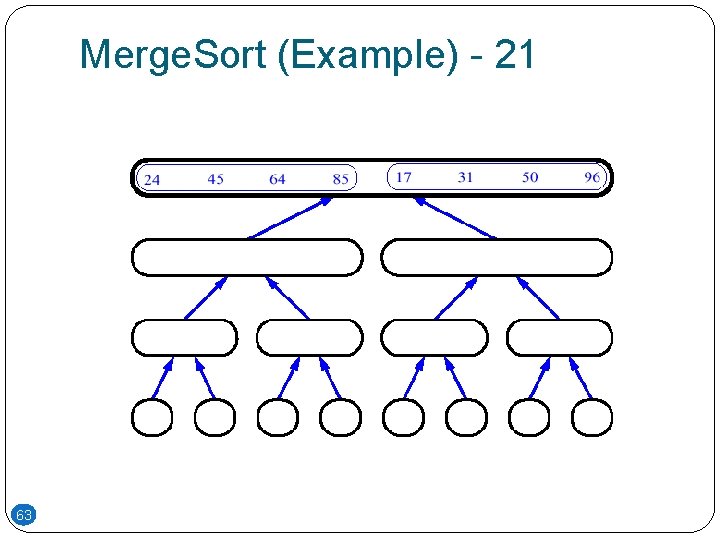
Merge. Sort (Example) - 21 63
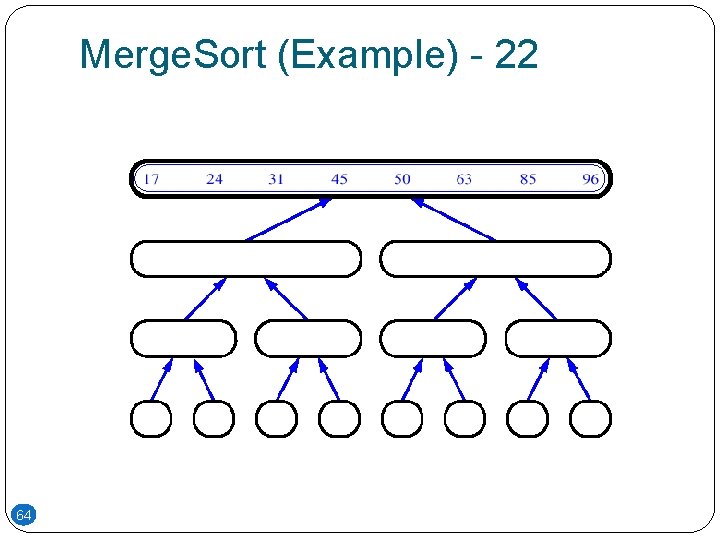
Merge. Sort (Example) - 22 64
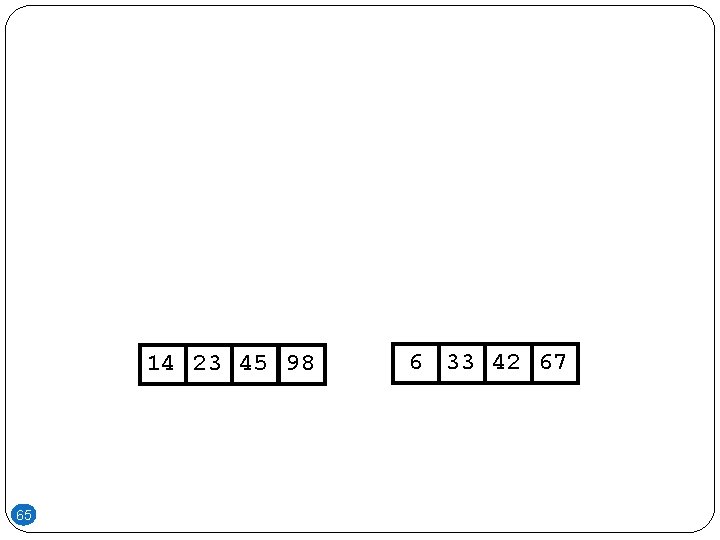
14 23 45 98 65 6 33 42 67
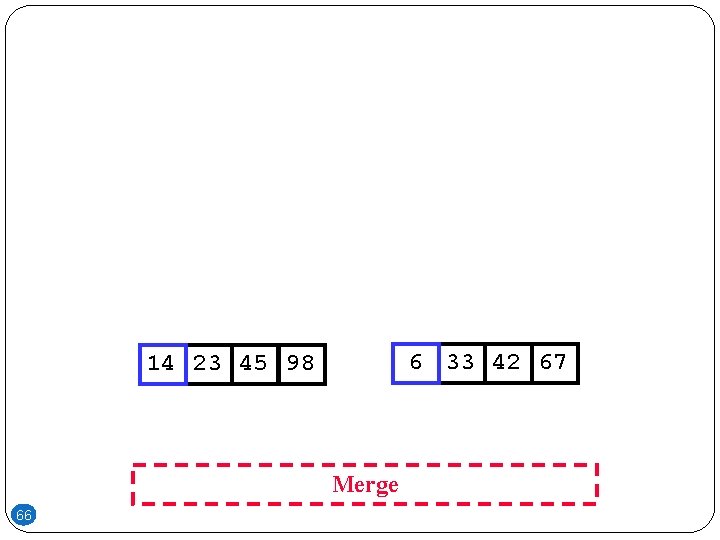
6 33 42 67 14 23 45 98 Merge 66
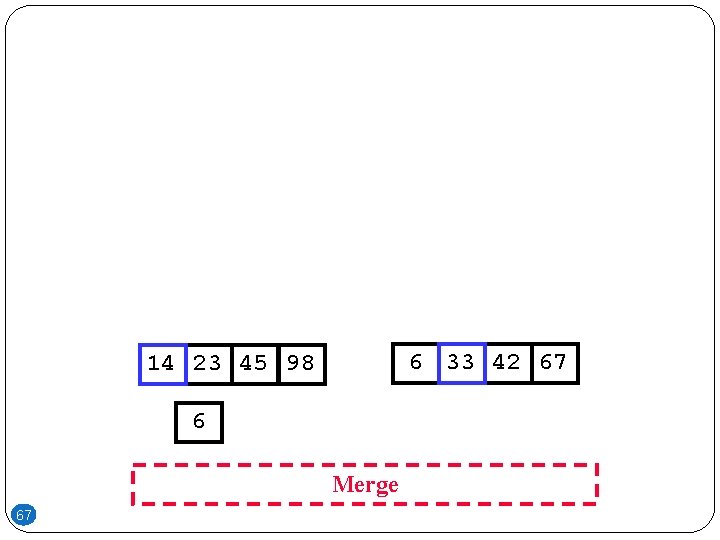
6 33 42 67 14 23 45 98 6 Merge 67
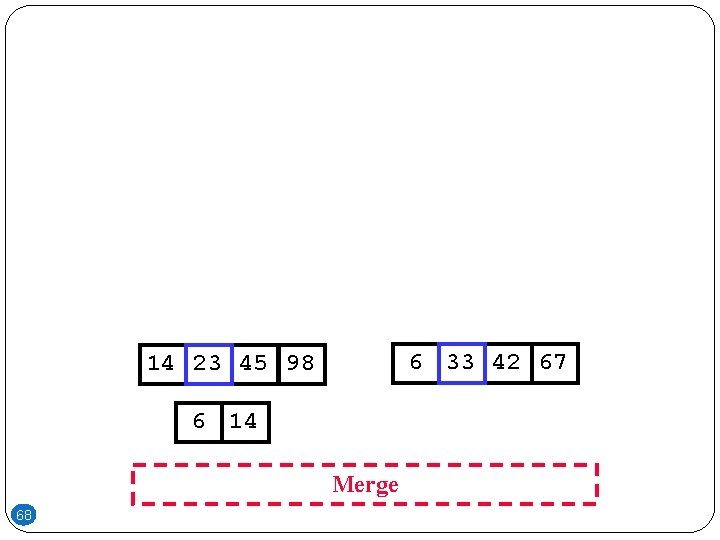
6 33 42 67 14 23 45 98 6 14 Merge 68
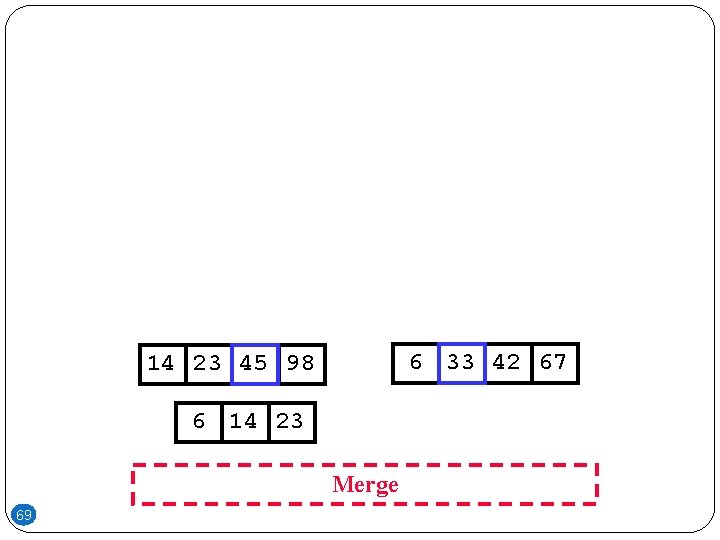
6 33 42 67 14 23 45 98 6 14 23 Merge 69
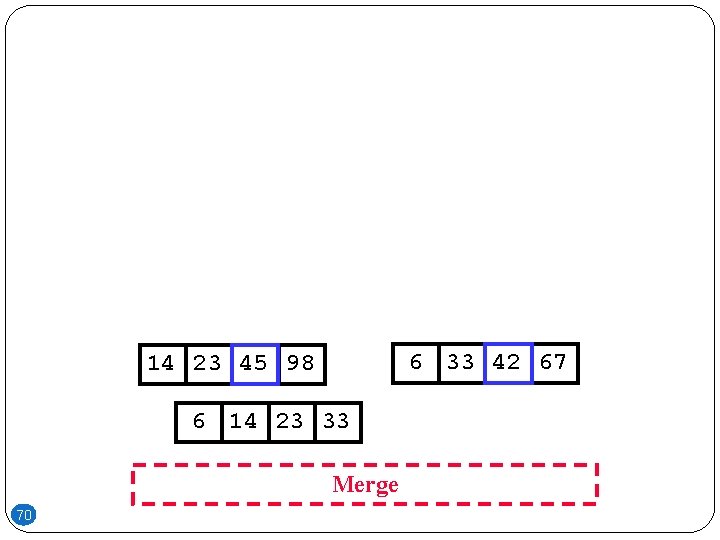
6 33 42 67 14 23 45 98 6 14 23 33 Merge 70
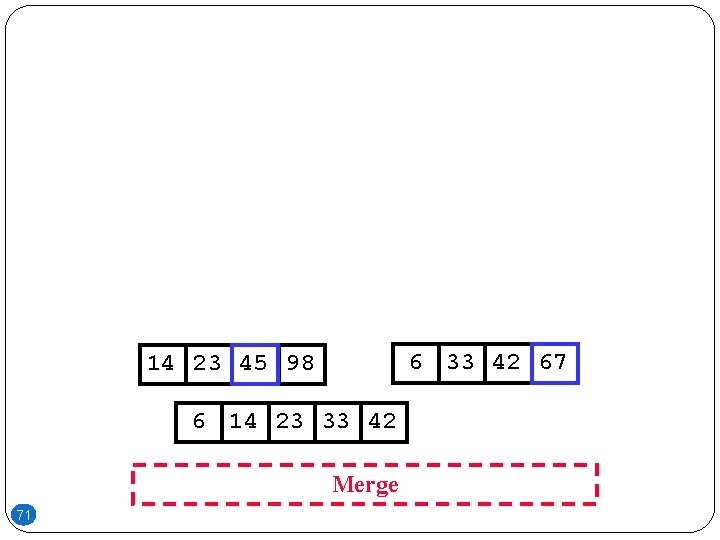
6 33 42 67 14 23 45 98 6 14 23 33 42 Merge 71
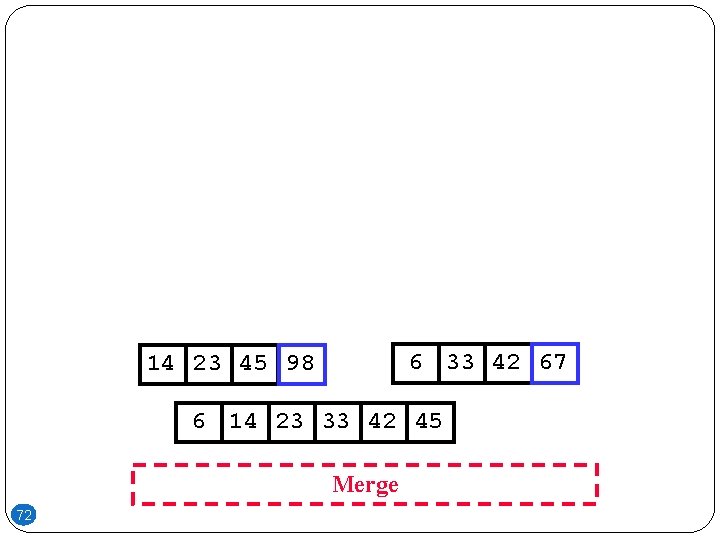
6 33 42 67 14 23 45 98 6 14 23 33 42 45 Merge 72
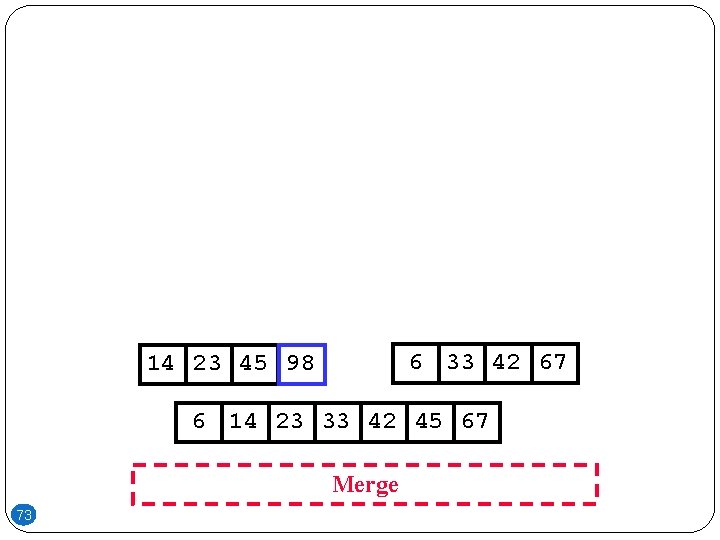
6 33 42 67 14 23 45 98 6 14 23 33 42 45 67 Merge 73
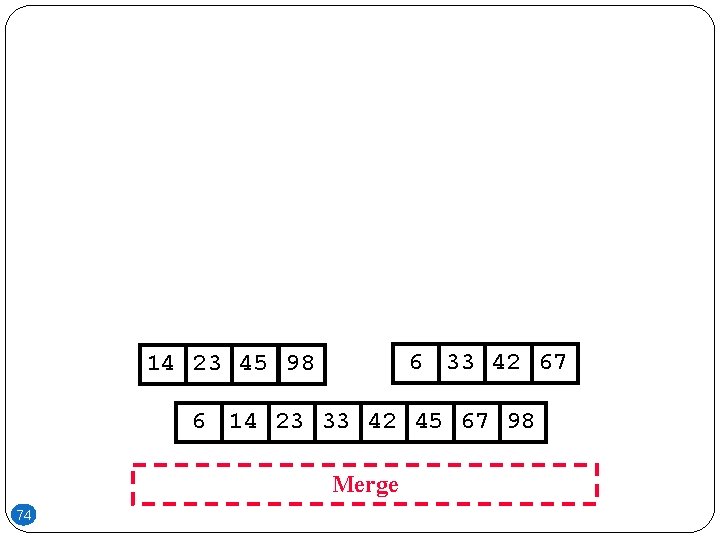
6 33 42 67 14 23 45 98 6 14 23 33 42 45 67 98 Merge 74

Merge Sort Example 75

Summary �Merge Sort Algorithm �Time Complexity �Best case �Average case �Worst case �Examples 76
- Slides: 76