Review Overview of Cryptography Classical Symmetric Cipher Substitution

Review • Overview of Cryptography • Classical Symmetric Cipher – Substitution Cipher – Transposition Cipher – Product Cipher • Modern Symmetric Ciphers (DES)

Basic Terminology • plaintext - the original message • ciphertext - the coded message • cipher - algorithm for transforming plaintext to ciphertext • key - info used in cipher known only to sender/receiver • encipher (encrypt) - converting plaintext to ciphertext • decipher (decrypt) - recovering ciphertext from plaintext • cryptography - study of encryption principles/methods • cryptanalysis (codebreaking) - the study of principles/ methods of deciphering ciphertext without knowing key • cryptology - the field of both cryptography and cryptanalysis

Feistel Cipher Structure • Feistel cipher implements Shannon’s S-P network concept – based on invertible product cipher • Process through multiple rounds which – partitions input block into two halves – perform a substitution on left data half – based on round function of right half & subkey – then have permutation swapping halves

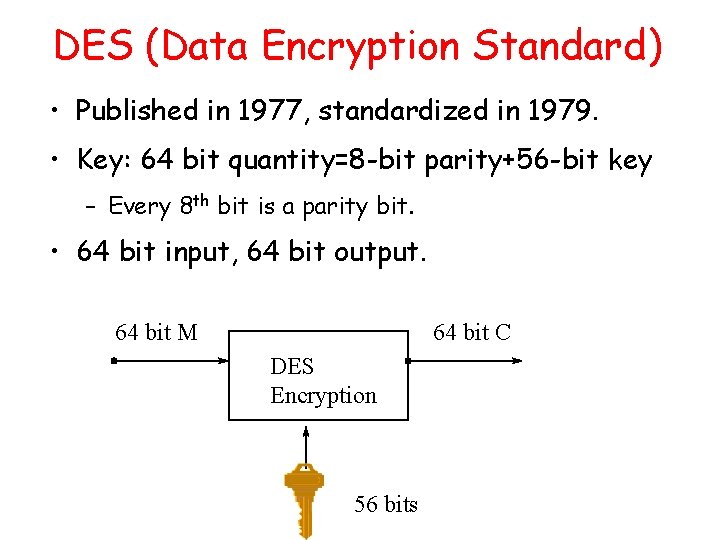
DES (Data Encryption Standard) • Published in 1977, standardized in 1979. • Key: 64 bit quantity=8 -bit parity+56 -bit key – Every 8 th bit is a parity bit. • 64 bit input, 64 bit output. 64 bit M 64 bit C DES Encryption 56 bits

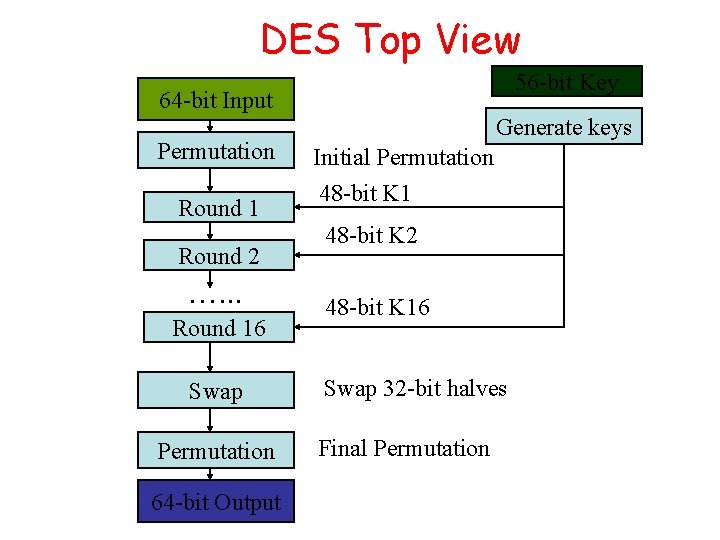
DES Top View 56 -bit Key 64 -bit 48 -bit. Input K 1 Permutation Round 1 Round 2 …. . . Round 16 Swap Permutation 64 -bit Output Generate keys Initial Permutation 48 -bit K 1 48 -bit K 2 48 -bit K 16 Swap 32 -bit halves Final Permutation

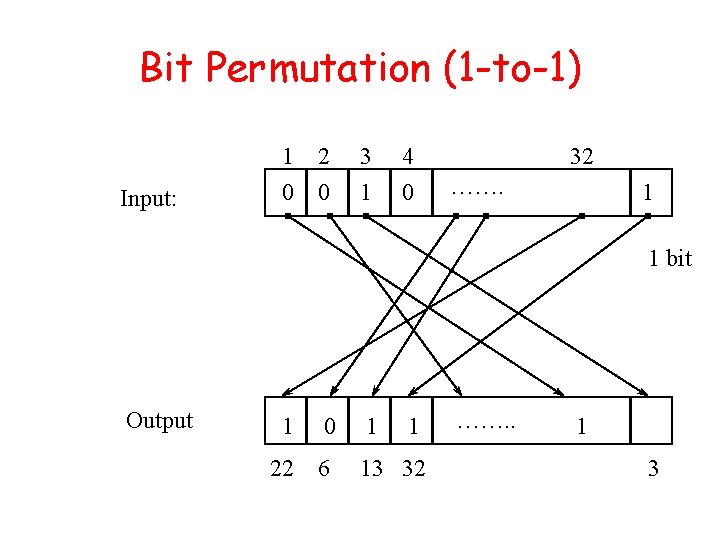
Bit Permutation (1 -to-1) Input: 1 2 0 0 3 1 4 0 32 ……. 1 1 bit Output 1 0 1 1 22 6 13 32 ……. . 1 3

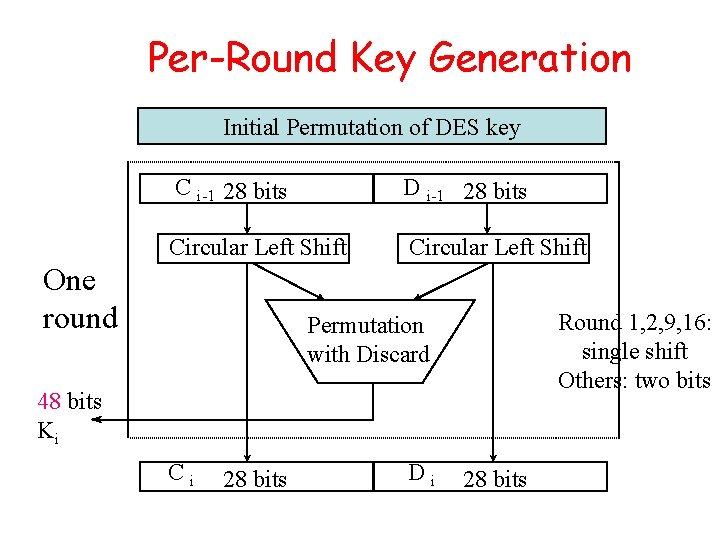
Per-Round Key Generation Initial Permutation of DES key C i-1 28 bits D i-1 28 bits Circular Left Shift One round Round 1, 2, 9, 16: single shift Others: two bits Permutation with Discard 48 bits Ki Ci 28 bits Di 28 bits

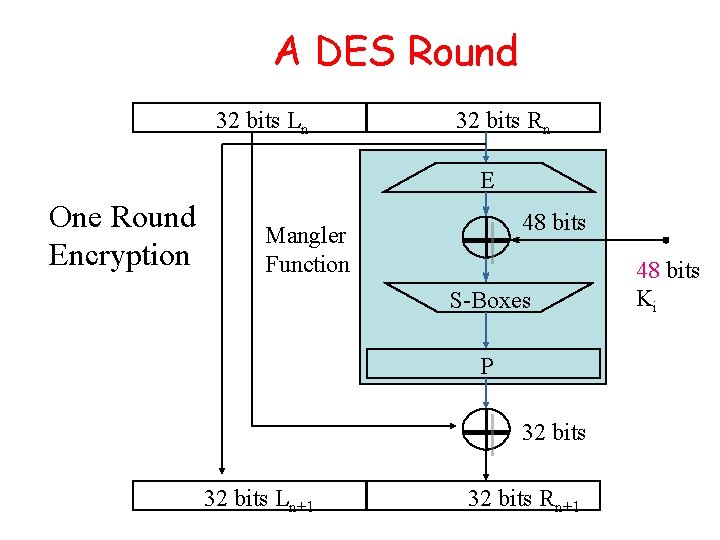
A DES Round 32 bits Ln 32 bits Rn E One Round Encryption 48 bits Mangler Function S-Boxes P 32 bits Ln+1 32 bits Rn+1 48 bits Ki

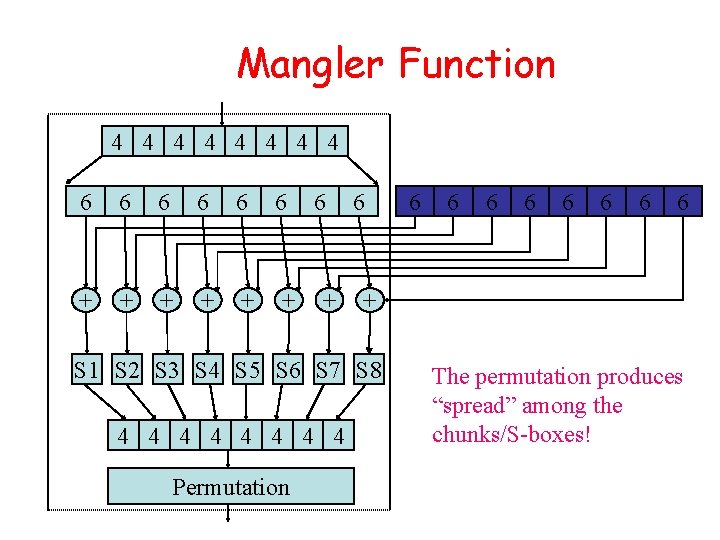
Mangler Function 4 4 4 4 6 6 6 + + + 6 + 6 Permutation 6 6 6 6 + S 1 S 2 S 3 S 4 S 5 S 6 S 7 S 8 4 4 4 4 6 The permutation produces “spread” among the chunks/S-boxes!

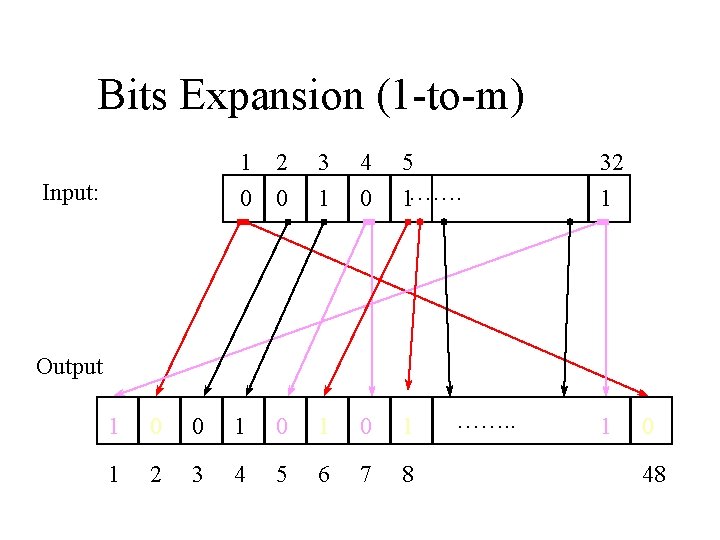
Bits Expansion (1 -to-m) Input: 1 0 2 0 3 1 4 0 5 1……. 32 1 Output 1 0 0 1 0 1 1 2 3 4 5 6 7 8 ……. . 1 0 48

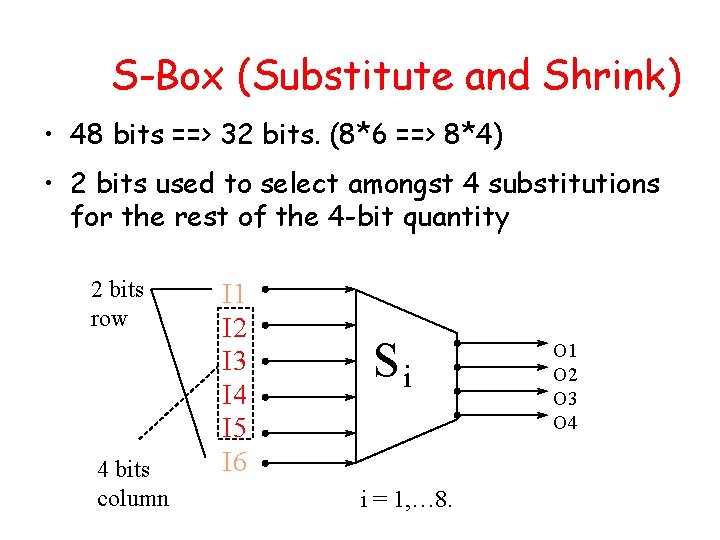
S-Box (Substitute and Shrink) • 48 bits ==> 32 bits. (8*6 ==> 8*4) • 2 bits used to select amongst 4 substitutions for the rest of the 4 -bit quantity 2 bits row 4 bits column I 1 I 2 I 3 I 4 I 5 I 6 Si i = 1, … 8. O 1 O 2 O 3 O 4

DES Standard • Cipher Iterative Action : – Input: 64 bits – Key: 48 bits • Key Generation Box : – Input: 56 bits – Output: 48 bits – Output: 64 bits One round (Total 16 rounds)

DES Box Summary • Simple, easy to implement: – Hardware/gigabits/second, software/megabits/second • 56 -bit key DES may be acceptable for noncritical applications but triple DES (DES 3) should be secure for most applications today • Supports several operation modes (ECB CBC, OFB, CFB) for different applications

Outlines • Strength/weakness of DES, AES • Public Key Cryptography • Modular Arithmetic • RSA

Avalanche Effect • Key desirable property of encryption alg • Where a change of one input or key bit results in changing more than half output bits • DES exhibits strong avalanche

Strength of DES – Key Size • 56 -bit keys have 256 = 7. 2 x 1016 values • Brute force search looks hard • Recent advances have shown is possible – in 1997 on a huge cluster of computers over the Internet in a few months – in 1998 on dedicated hardware called “DES cracker” by EFF in a few days ($220, 000) – in 1999 above combined in 22 hrs! • Still must be able to recognize plaintext • No big flaw for DES algorithms

DES Replacement • Triple-DES (3 DES) – 168 -bit key, no brute force attacks – Underlying encryption algorithm the same, no effective analytic attacks – Drawbacks • Performance: no efficient software codes for DES/3 DES • Efficiency/security: bigger block size desirable • Advanced Encryption Standards (AES) – US NIST issued call for ciphers in 1997 – Rijndael was selected as the AES in Oct-2000

AES • Private key symmetric block cipher • 128 -bit data, 128/192/256 -bit keys • Stronger & faster than Triple-DES • Provide full specification & design details • Evaluation criteria – Security: effort to practically cryptanalysis – Cost: computational efficiency and memory requirement – Algorithm & implementation characteristics: flexibility to apps, hardware/software suitability, simplicity

AES Shortlist • After testing and evaluation, shortlist in Aug-99: – MARS (IBM) - complex, fast, high security margin – RC 6 (USA) - v. simple, v. fast, low security margin – Rijndael (Belgium) - clean, fast, good security margin – Serpent (Euro) - slow, clean, v. high security margin – Twofish (USA) - complex, v. fast, high security margin • Then subject to further analysis & comment

Outlines • Strength/weakness of DES, AES • Public Key Cryptography • Modular Arithmetic • RSA

Private-Key Cryptography • Private/secret/single key cryptography uses one key • Shared by both sender and receiver • If this key is disclosed communications are compromised • Also is symmetric, parties are equal • Hence does not protect sender from receiver forging a message & claiming is sent by sender

Public-Key Cryptography • Probably most significant advance in the 3000 year history of cryptography • Uses two keys – a public & a private key • Asymmetric since parties are not equal • Uses clever application of number theoretic concepts to function • Complements rather than replaces private key crypto

Public-Key Cryptography • Public-key/two-key/asymmetric cryptography involves the use of two keys: – a public-key, which may be known by anybody, and can be used to encrypt messages, and verify signatures – a private-key, known only to the recipient, used to decrypt messages, and sign (create) signatures • Asymmetric because – those who encrypt messages or verify signatures cannot decrypt messages or create signatures

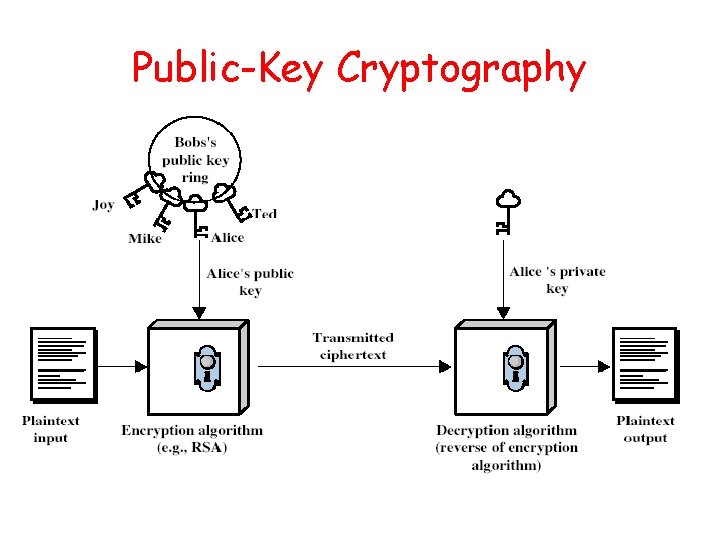
Public-Key Cryptography

Public-Key Characteristics • Public-Key algorithms rely on two keys with the characteristics that it is: – computationally infeasible to find decryption key knowing only algorithm & encryption key – computationally easy to en/decrypt messages when the relevant (en/decrypt) key is known – either of the two related keys can be used for encryption, with the other used for decryption (in some schemes) • Analogy to delivery w/ a padlocked box

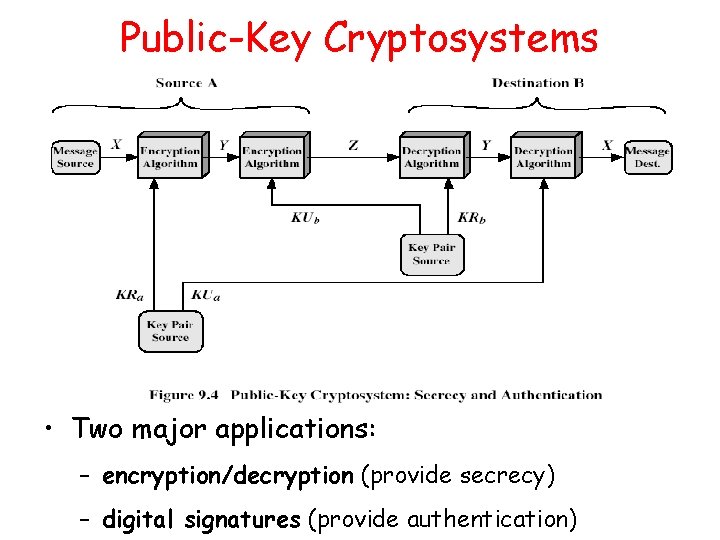
Public-Key Cryptosystems • Two major applications: – encryption/decryption (provide secrecy) – digital signatures (provide authentication)

Outlines • Strength/weakness of DES, AES • Public Key Cryptography • Modular Arithmetic • RSA

Modular Arithmetic • Public key algorithms are based on modular arithmetic. • Modular addition. • Modular multiplication. • Modular exponentiation.

Modular Addition • Addition modulo (mod) K – Poor cipher with (dk+dm) mod K, e. g. , if K=10 and dk is the key. + 0 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 1 1 2 3 4 5 6 7 8 9 0 2 2 3 4 5 6 7 8 9 0 1 3 3 4 5 6 7 8 9 0 1 2 • Additive inverse: addition mod K yields 0. • “Decrypt” by adding inverse.

Modular Multiplication • Multiplication modulo K * 0 1 2 3 4 5 6 7 8 9 0 0 0 1 2 3 4 5 6 7 8 9 2 0 2 4 6 8 3 0 3 6 9 2 5 8 1 4 7 • Multiplicative inverse: multiplication mod K yields 1 • Only some numbers have inverse

Modular Multiplication • Only the numbers relatively prime to n will have mod n multiplicative inverse • x, m relative prime: no other common factor than 1 – Eg. 8 & 15 are relatively prime - factors of 8 are 1, 2, 4, 8 and of 15 are 1, 3, 5, 15 and 1 is the only common factor

Totient Function • Totient function ø(n): number of integers less than n relatively prime to n – if n is prime, • ø(n)=n-1 – if n=p q, and p, q are primes, p != q • ø(n)=(p-1)(q-1) – E. g. , • ø(37) = 36 • ø(21) = (3– 1)×(7– 1) = 2× 6 = 12

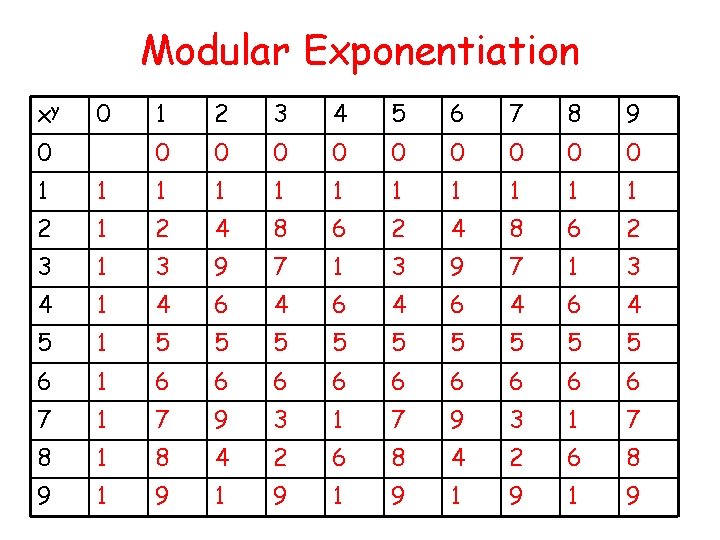
Modular Exponentiation xy 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 1 1 1 2 4 8 6 2 3 1 3 9 7 1 3 4 1 4 6 4 6 4 5 1 5 5 5 5 5 6 1 6 6 6 6 6 7 1 7 9 3 1 7 8 1 8 4 2 6 8 9 1 9 1 9 1 9

Modular Exponentiation • xy mod n = xy mod ø(n) mod n • if y = 1 mod ø(n) then xy mod n = x mod n

Outlines • Strength/weakness of DES, AES • Public Key Cryptography • Modular Arithmetic • RSA

RSA (Rivest, Shamir, Adleman) • The most popular one. • Support both public key encryption and digital signature. • Assumption/theoretical basis: – Factoring a big number is hard. • Variable key length (usually 512 bits). • Variable plaintext block size. – Plaintext must be “smaller” than the key. – Ciphertext block size is the same as the key length.

What Is RSA? • To generate key pair: – Pick large primes (>= 256 bits each) p and q – Let n = p*q, keep your p and q to yourself! – For public key, choose e that is relatively prime to ø(n) =(p-1)(q-1), let pub = <e, n> – For private key, find d that is the multiplicative inverse of e mod ø(n), i. e. , e*d = 1 mod ø(n), let priv = <d, n>

RSA Example 1. Select primes: p=17 & q=11 2. Compute n = pq =17× 11=187 3. Compute ø(n)=(p– 1)(q-1)=16× 10=160 4. Select e : gcd(e, 160)=1; choose e=7 5. Determine d: de=1 mod 160 and d < 160 Value is d=23 since 23× 7=161= 10× 160+1 6. Publish public key KU={7, 187} 7. Keep secret private key KR={23, 17, 11}

How Does RSA Work? • Given pub = <e, n> and priv = <d, n> – encryption: c = me mod n, m < n – decryption: m = cd mod n – signature: s = md mod n, m < n – verification: m = se mod n • given message M = 88 (nb. 88<187) • encryption: C = 887 mod 187 = 11 • decryption: M = 1123 mod 187 = 88

Why Does RSA Work? • Given pub = <e, n> and priv = <d, n> – n =p*q, ø(n) =(p-1)(q-1) – e*d = 1 mod ø(n) – xe d = x mod n – encryption: c = me mod n – decryption: m = cd mod n = me d mod n = m (since m < n) – digital signature (similar)

Is RSA Secure? • Factoring 512 -bit number is very hard! • But if you can factor big number n then given public key <e, n>, you can find d, hence the private key by: – Knowing factors p, q, such that, n = p*q – Then ø(n) =(p-1)(q-1) – Then d such that e*d = 1 mod ø(n) • Threat – Moore’s law – Refinement of factorizing algorithms • For the near future, a key of 1024 or 2048 bits needed

Symmetric (DES) vs. Public Key (RSA) • Exponentiation of RSA is expensive ! • AES and DES are much faster – 100 times faster in software – 1, 000 to 10, 000 times faster in hardware • RSA often used in combination in AES and DES – Pass the session key with RSA