Review on Magnetism Chapter 28 Magnetism 1 Magnetism

Review on Magnetism Chapter 28 Magnetism 1

Magnetism • Refrigerators are attracted to magnets! Magnetism 2

Where is Magnetism Used? ? • Motors • Navigation – Compass • Magnetic Tapes – Music, Data • Television – Beam deflection Coil • Magnetic Resonance Imaging (MRI) • High Energy Physics Research Magnetism 3

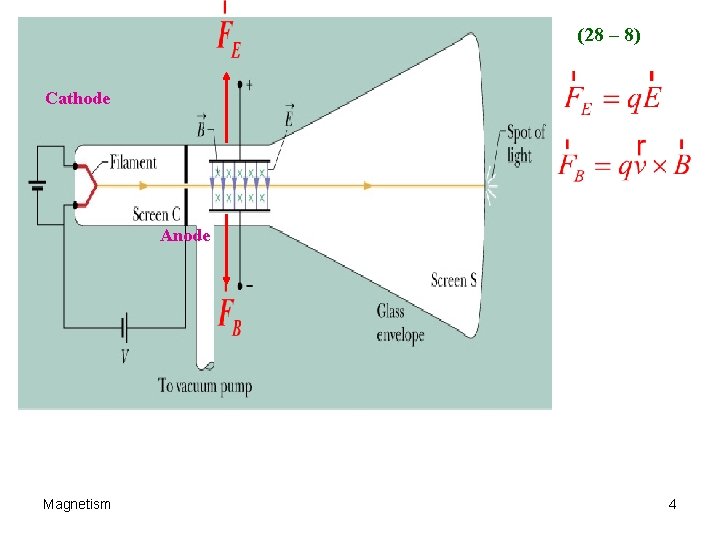
(28 – 8) Cathode Anode Magnetism 4

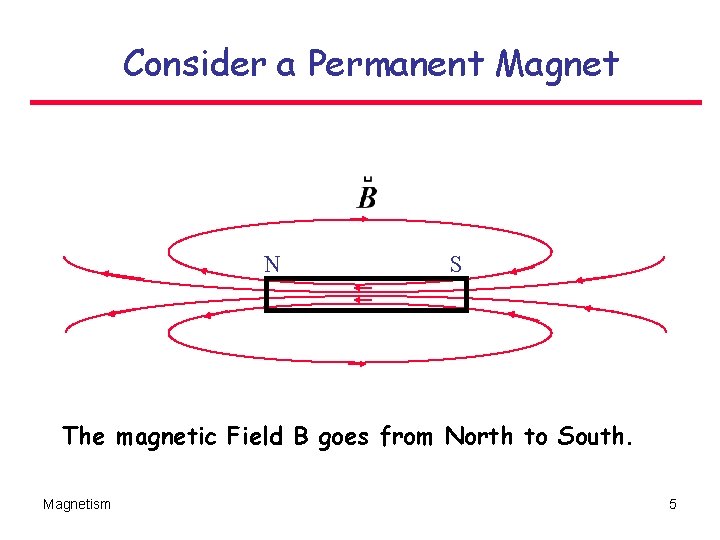
Consider a Permanent Magnet N S The magnetic Field B goes from North to South. Magnetism 5

Units Magnetism 6

Typical Representation Magnetism 7

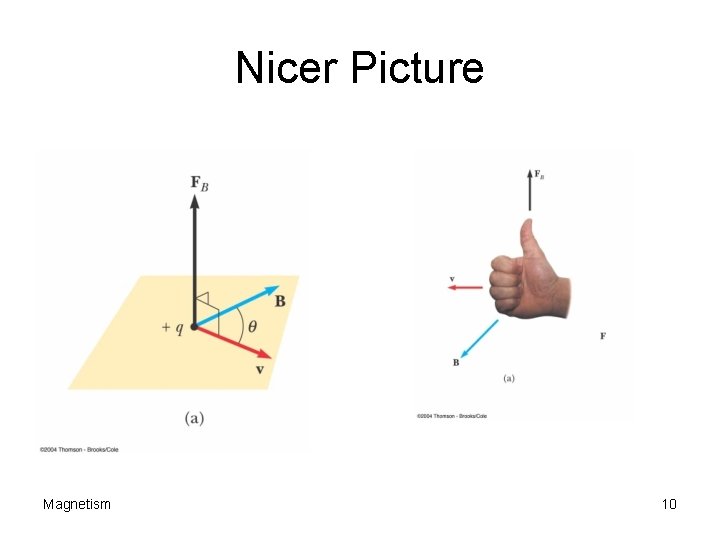
A Look at the Physics q There is NO force on a charge placed into a magnetic field if the charge is NOT moving. There is no force if the charge moves parallel to the field. q • If the charge is moving, there is a force on the charge, perpendicular to both v and B. F=qvx. B Magnetism 8

The Lorentz Force This can be summarized as: F or: v B mq q is the angle between B and V Magnetism 9

Nicer Picture Magnetism 10

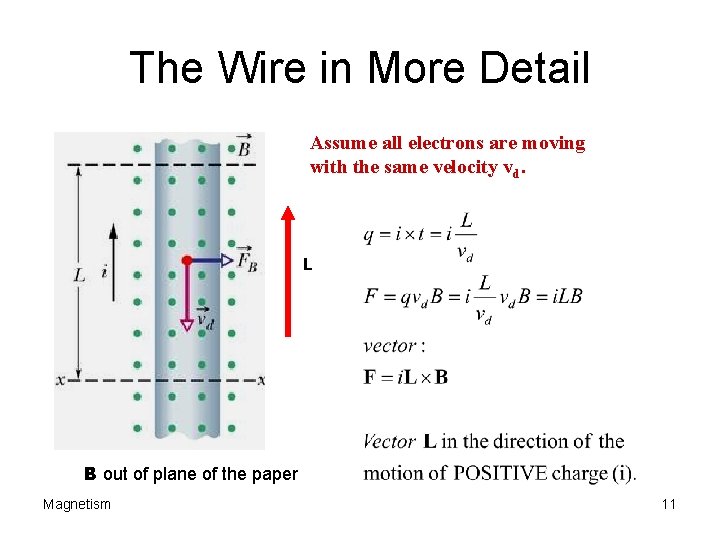
The Wire in More Detail Assume all electrons are moving with the same velocity vd. L B out of plane of the paper Magnetism 11

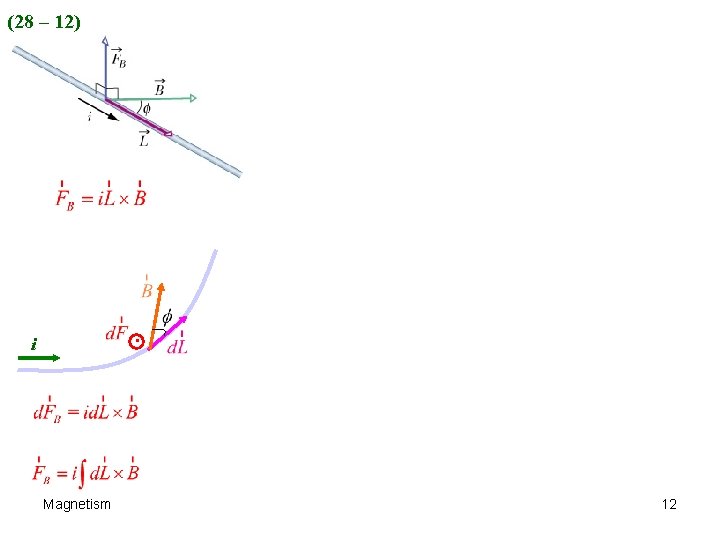
(28 – 12) . i Magnetism 12

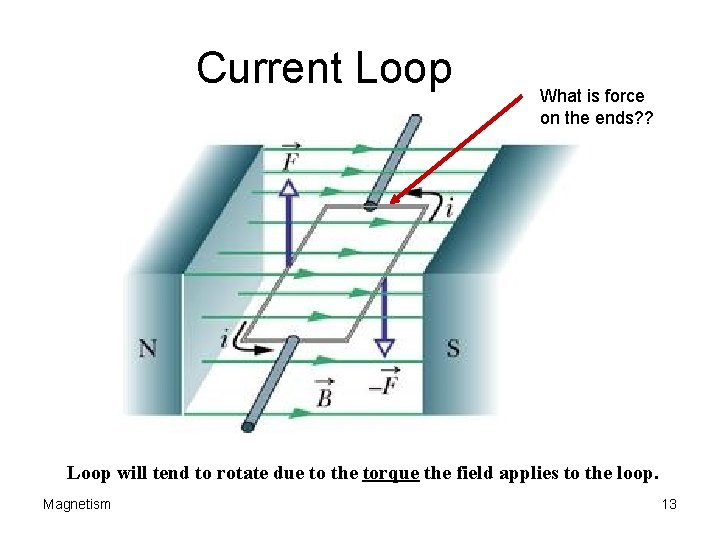
Current Loop What is force on the ends? ? Loop will tend to rotate due to the torque the field applies to the loop. Magnetism 13

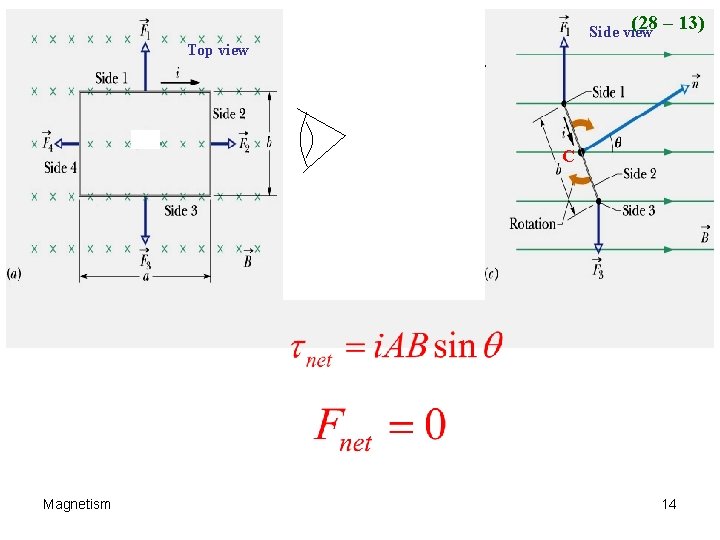
(28 – 13) Side view Top view C C Magnetism 14

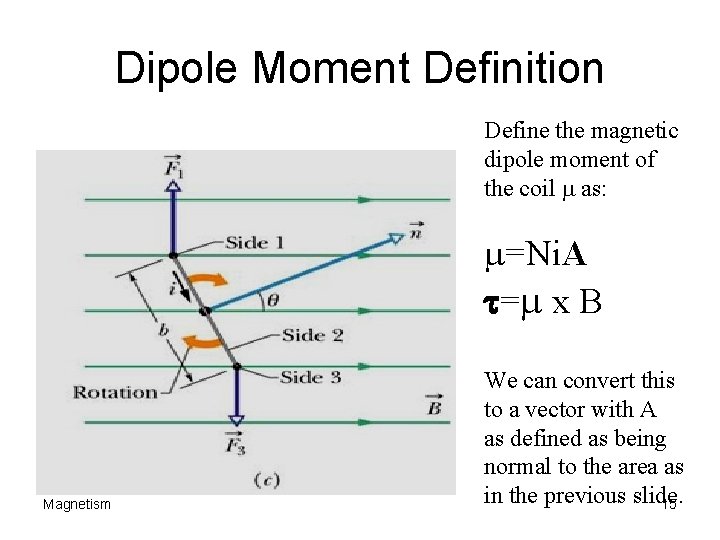
Dipole Moment Definition Define the magnetic dipole moment of the coil m as: m=Ni. A t=m x B Magnetism We can convert this to a vector with A as defined as being normal to the area as in the previous slide. 15

Magnetism 16 (28 – 14)

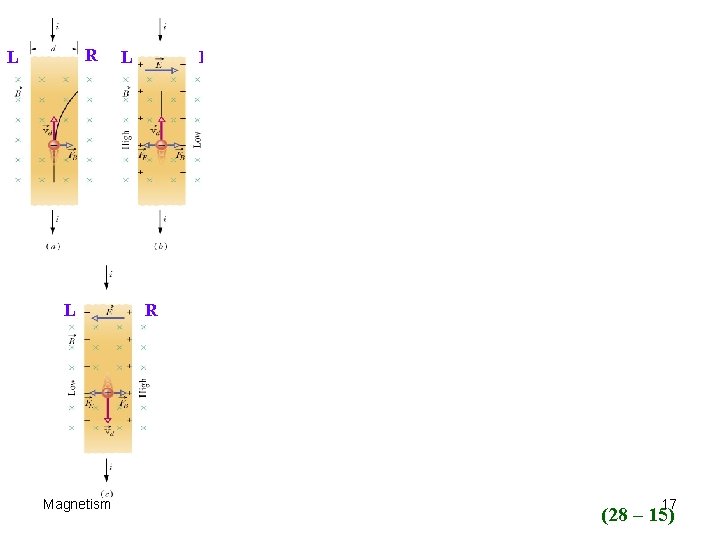
R L L Magnetism L R R 17 (28 – 15)

Motion of a charged particle in a magnetic Field Magnetism 18

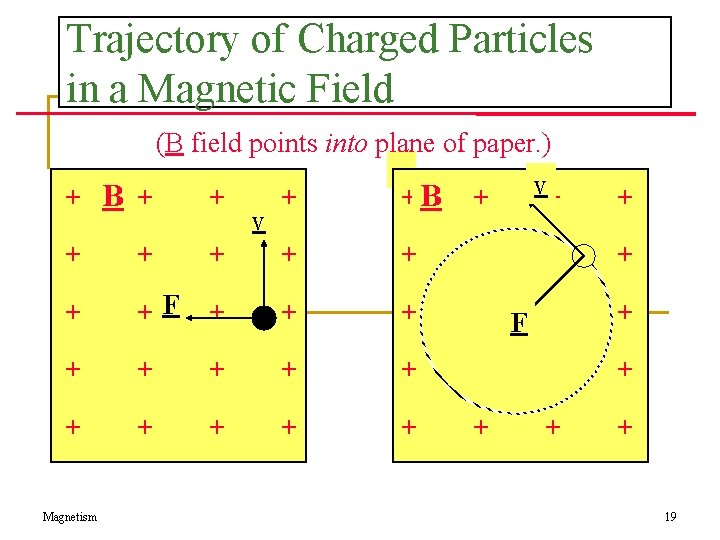
Trajectory of Charged Particles in a Magnetic Field (B field points into plane of paper. ) + +B + v+ + + + + F + + + + + + B + + + Magnetism v 19

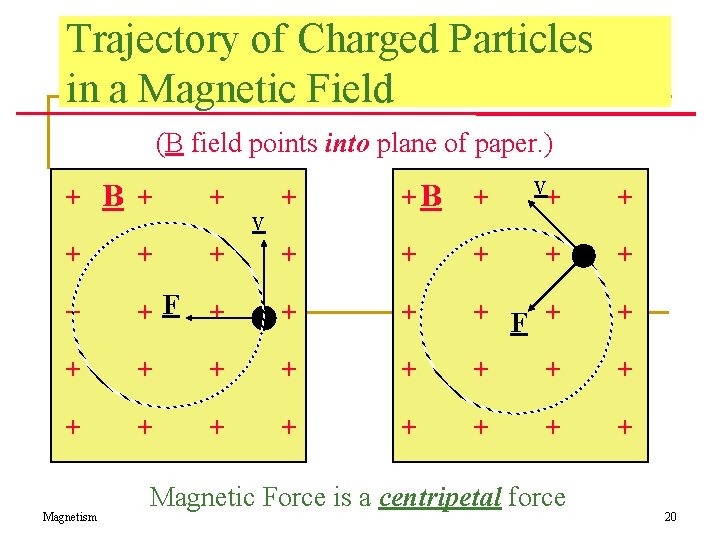
Trajectory of Charged Particles in a Magnetic Field (B field points into plane of paper. ) v+ + B + +B + v + + + F + + + + + + Magnetism Magnetic Force is a centripetal force 20

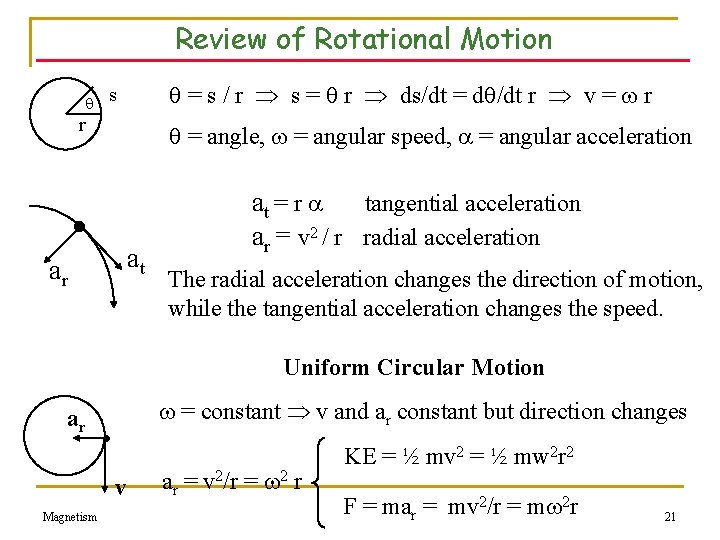
Review of Rotational Motion = s / r s = r ds/dt = d /dt r v = r s r = angle, = angular speed, = angular acceleration at ar at = r tangential acceleration ar = v 2 / r radial acceleration The radial acceleration changes the direction of motion, while the tangential acceleration changes the speed. Uniform Circular Motion ar = constant v and ar constant but direction changes v Magnetism ar = v 2/r = 2 r KE = ½ mv 2 = ½ mw 2 r 2 F = mar = mv 2/r = m 2 r 21

Magnetism 22

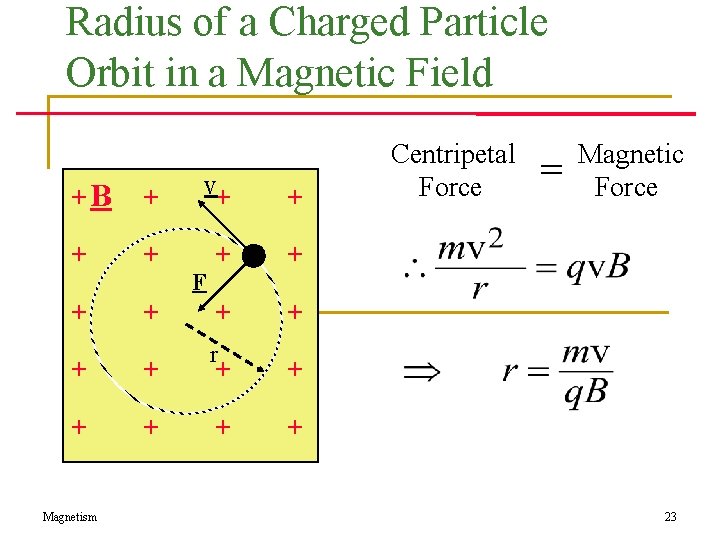
Radius of a Charged Particle Orbit in a Magnetic Field +B + v+ + + r + + + Magnetism F + Centripetal Force = Magnetic Force 23

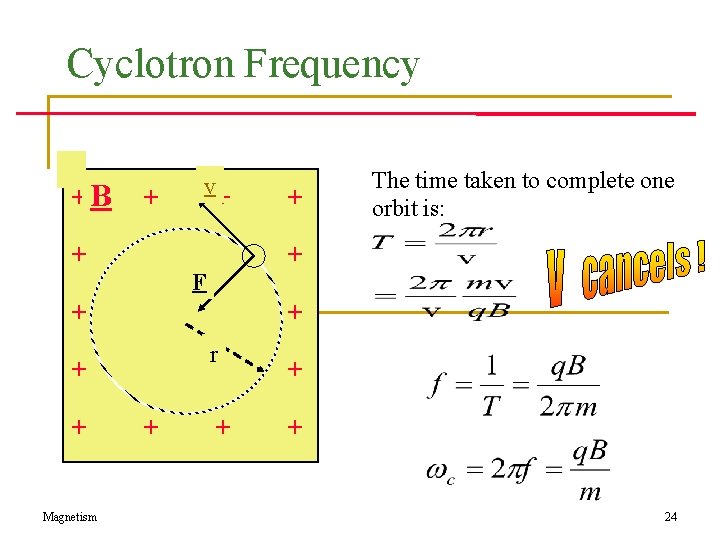
Cyclotron Frequency +B + v + + + r + + + Magnetism F + The time taken to complete one orbit is: 24

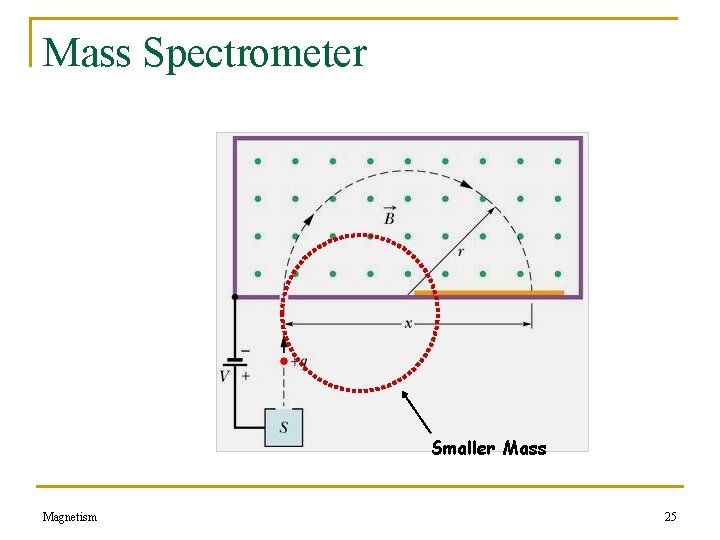
Mass Spectrometer Smaller Mass Magnetism 25

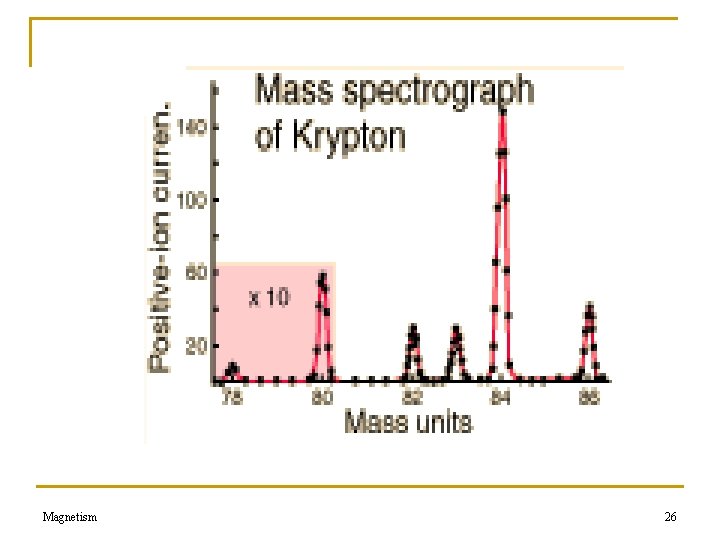
Magnetism 26

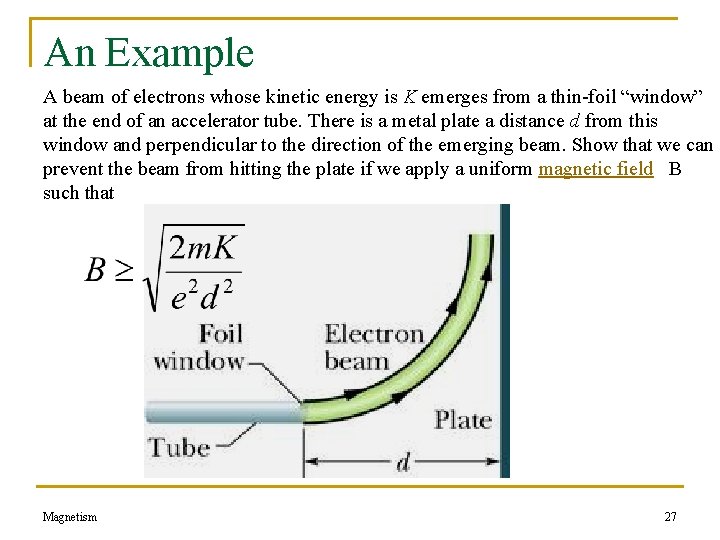
An Example A beam of electrons whose kinetic energy is K emerges from a thin-foil “window” at the end of an accelerator tube. There is a metal plate a distance d from this window and perpendicular to the direction of the emerging beam. Show that we can prevent the beam from hitting the plate if we apply a uniform magnetic field B such that Magnetism 27

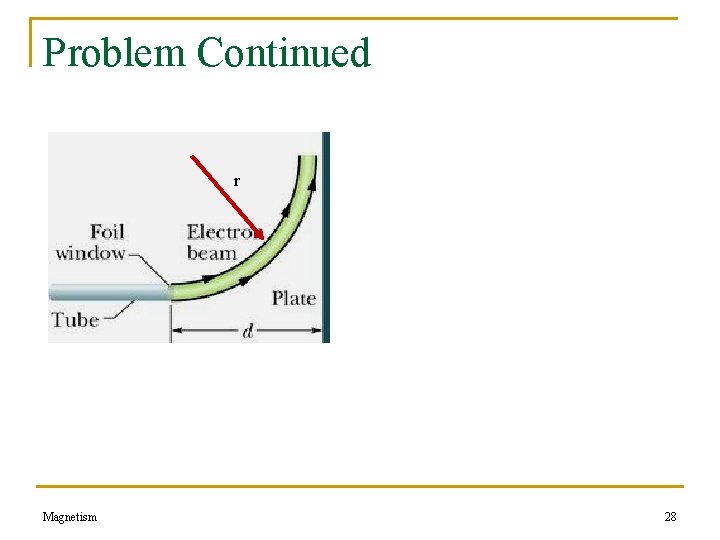
Problem Continued r Magnetism 28

#14 Chapter 28 A metal strip 6. 50 cm long, 0. 850 cm wide, and 0. 760 mm thick moves with constant velocity through a uniform magnetic field B= 1. 20 m. Tdirected perpendicular to the strip, as shown in the Figure. A potential difference of 3. 90 ηV is measured between points x and y across the strip. Calculate the speed v. FIGURE 2837 Magnetism Problem 14. 29

n 21. (a) Find the frequency of revolution of an electron with an energy of 100 e. V in a uniform magnetic field of magnitude 35. 0 µT. (b) Calculate the radius of the path of this electron if its velocity is perpendicular to the magnetic field. Magnetism 30

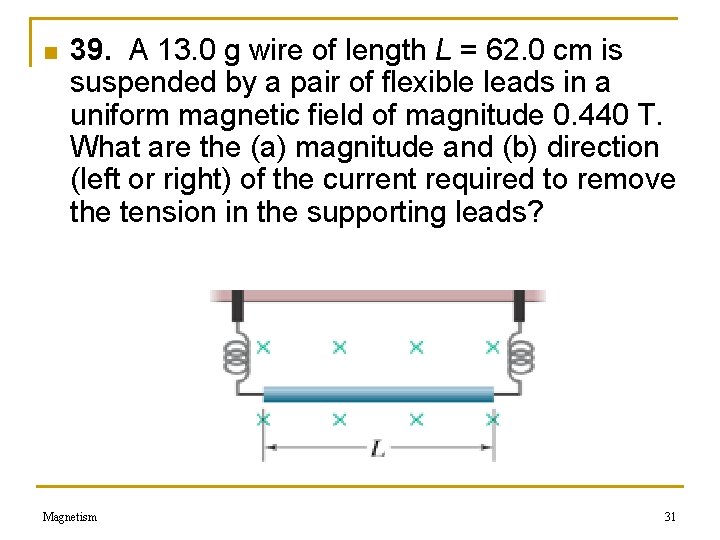
n 39. A 13. 0 g wire of length L = 62. 0 cm is suspended by a pair of flexible leads in a uniform magnetic field of magnitude 0. 440 T. What are the (a) magnitude and (b) direction (left or right) of the current required to remove the tension in the supporting leads? Magnetism 31