Review of Sequential Representations Previously introduced data structures

Review of Sequential Representations • Previously introduced data structures, including array, queue, and stack, they all have the property that successive nodes of data object were stored a fixed distance apart. • The drawback of sequential mapping for ordered lists is that operations such as insertion and deletion become expensive. • Also sequential representation tends to have less space efficiency when handling multiple various sizes of ordered lists.

Linked List • A better solutions to resolve the aforementioned issues of sequential representations is linked lists. • Elements in a linked list are not stored in sequential in memory. Instead, they are stored all over the memory. They form a list by recording the address of next element for each element in the list. Therefore, the list is linked together. • A linked list has a head pointer that points to the first element of the list. • By following the links, you can traverse the linked list and visit each element in the list one by one.

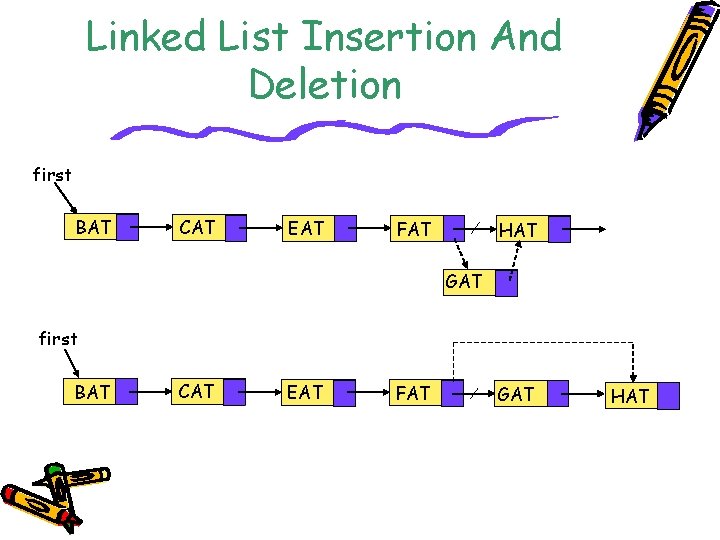
Linked List Insertion • To insert an element into the three letter linked list: – Get a node that is currently unused; let its address be x. – Set the data field of this node to GAT. – Set the link field of x to point to the node after FAT, which contains HAT. – Set the link field of the node cotaining FAT to x.

Linked List Insertion And Deletion first BAT CAT EAT FAT HAT GAT first BAT CAT EAT FAT GAT HAT

Designing a List in C++ • Design Attempt 1: Use a global variable first which is a pointer of Three. Letter. Node. – Unable to access to private data members: data and link. • Design Attempt 2: Make member functions public. – Defeat the purpose of data encapsulation. • Design Attempt 3: Use of two classes. Create a class that represents the linked list. The class contains the items of another objects of another class.

Program 4. 1 Composite Classes class Three. Letter. List; // forward delcarion class Three. Letter. Node { friend class Three. Letter. List; private: char data[3]; Three. Letter. Node * link; }; class Three. Letter. List { public: // List Manipulation operations. . private: Three. Letter. Node *first; };

Nested Classes • The Three Letter List problem can also use nested classes to represent its structure. class Three. Letter. List { public: // List Manipulation operations. . private: class Three. Letter. Node { // nested class public: char data[3]; Three. Letter. Node *link; }; Three. Letter. Node *first; };

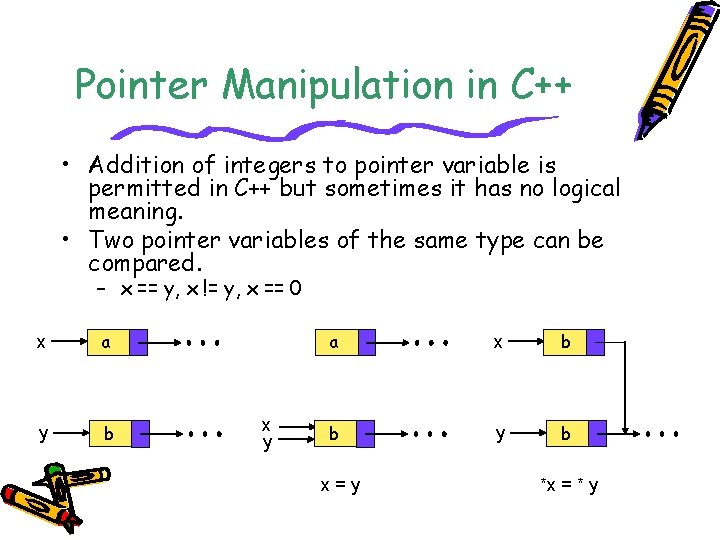
Pointer Manipulation in C++ • Addition of integers to pointer variable is permitted in C++ but sometimes it has no logical meaning. • Two pointer variables of the same type can be compared. – x == y, x != y, x == 0 x a y b x y a x b b y b x=y *x = * y

Define A Linked List Template • A linked list is a container class, so its implementation is a good template candidate. • Member functions of a linked list should be general that can be applied to all types of objects. • When some operations are missing in the original linked list definition, users should not be forced to add these into the original class design. • Users should be shielded from the detailed implementation of a linked list while be able to traverse the linked list. Solution => Use of List. Iterator

List Iterator • A list iterator is an object that is used to traverse all the elements of a container class. • List. Iterator<Type> is delcared as a friend of both List<Type> and List. Node<Type>. • A List. Iterator<Type> object is initialized with the name of a List<Type> object l with which it will be associated. • The List. Iterator<Type> object contains a private data member current of type List. Node<Type> *. At all times, current points to a node of list l. • The List. Iterator<Type> object defines public member functions Not. Null(), Next. Not. Null(), First(), and Next() to perform various tests on and to retrieve elements of l.

Program 4. 8 Template of Linked Lists Enum Boolean { FALSE, TRUE}; template <class Type> class List. Iterator; template <class Type> class List. Node { friend class List<Type>; friend class List. Iterator <Type>; private: Type data; List. Node *link; }; Template <class Type> class List { friend class List. Iterator <Type>; public: List() {first = 0; }; // List manipulation operations. . private: List. Node <Type> *first; };

Program 4. 8 Template of Linked Lists (Cont. ) template <class Type> class List. Iterator { public: List. Iterator(const List<Type> &l): list(l), current(l. first) {}; Boolean Not. Null(); Boolean Next. Not. Null(); Type * First(); Type * Next(); Private: const List<Type>& list; // refers to an existing list List. Node<Type>* current; // points to a node in list };

Program 4. 11 Attaching A Node To The End Of A List Template <class Type> Void List<Type>: : Attach(Type k) { List. Node<Type>*newnode = new List. Node<Type>(k); if (first == 0) first = last =newnode; else { last->link = newnode; last = newnode; } };

Program 4. 13 Concatenating Two Chains Template <class Type> void List<Type>: : Concatenate(List<Type> b) // this = (a 1, …, am) and b = (b 1, …, bn) m, n ≥ , // produces the new chain z = (a 1, …, am, b 1, bn) in this. { if (!first) { first = b. first; return; } if (b. first) { for (List. Node<Type> *p = first; p->link; p = p->link); // no body p->link = b. first; } }

When Not To Reuse A Class • If efficiency becomes a problem when reuse one class to implement another class. • If the operations required by the application are complex and specialized, and therefore not offered by the class.

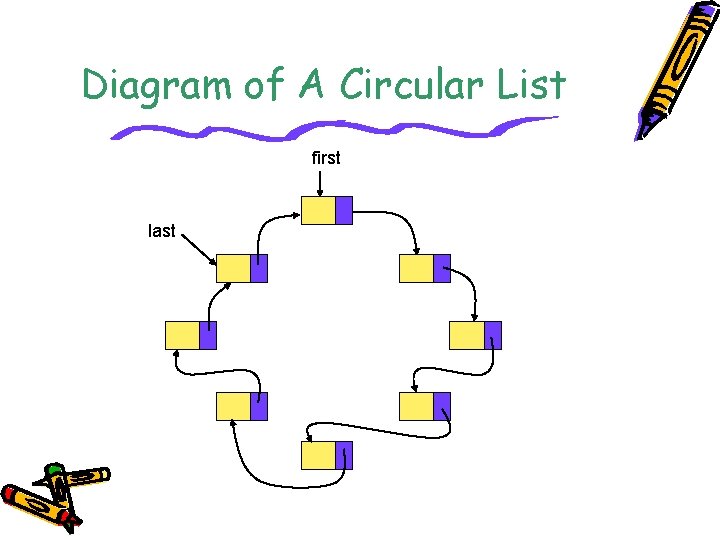
Circular Lists • By having the link of the last node points to the first node, we have a circular list. – Need to make sure when current is pointing to the last node by checking for current->link == first. – Insertion and deletion must make sure that the circular structure is not broken, especially the link between last node and first node.

Diagram of A Circular List first last

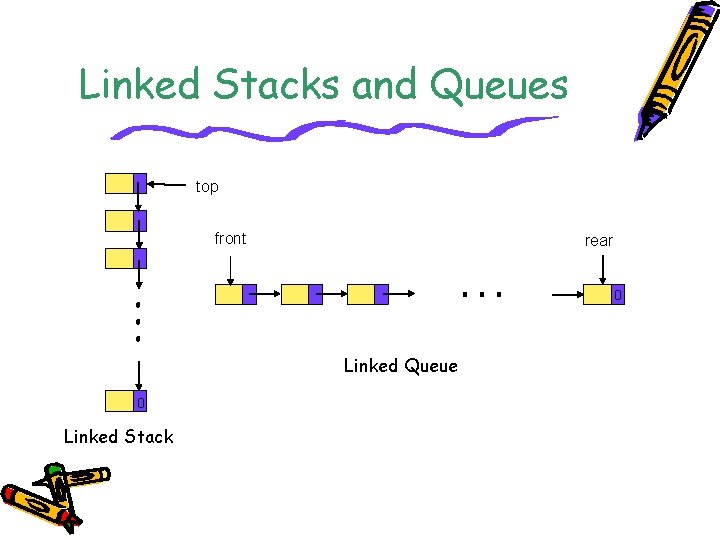
Linked Stacks and Queues top front rear 0 Linked Queue 0 Linked Stack

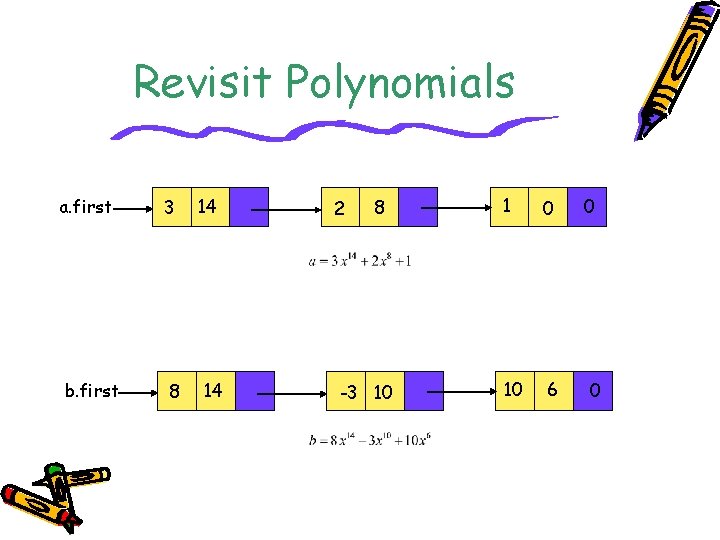
Revisit Polynomials a. first b. first 3 8 14 14 2 8 -3 10 1 0 10 6 0 0

Program 4. 20 Polynomial Class Definition struct Term // all members of Terms are public by default { int coef; // coefficient int exp; // exponent void Init(int c, int e) {coef = c; exp = e; }; }; class Polynomial { friend Polynomial operator+(const Polynomial&, const Polynomial&); private: List<Term> poly; };

Operating On Polynomials • With linked lists, it is much easier to perform operations on polynomials such as adding and deleting. – E. g. , adding two polynomials a and b a. first 3 14 2 8 1 0 0 -3 10 10 6 0 p b. first 8 14 q c. first 11 14 0 (i) p->exp == q->exp

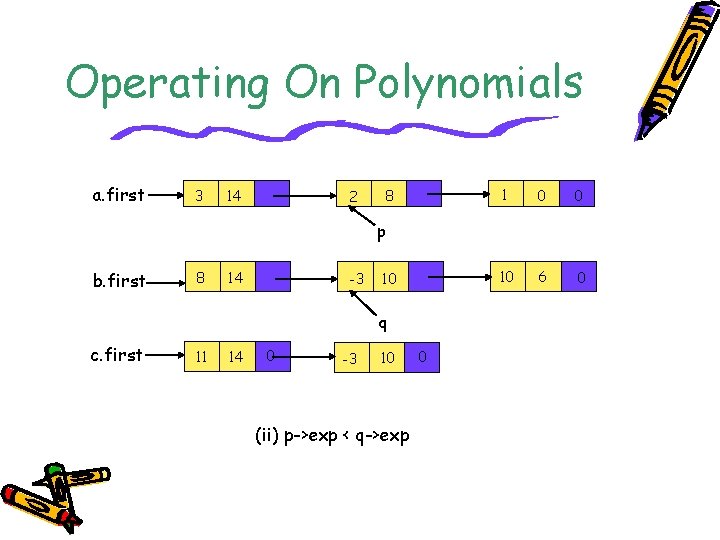
Operating On Polynomials a. first 3 14 2 8 1 0 0 10 6 0 p b. first 8 14 -3 10 q c. first 11 14 0 -3 10 (ii) p->exp < q->exp 0

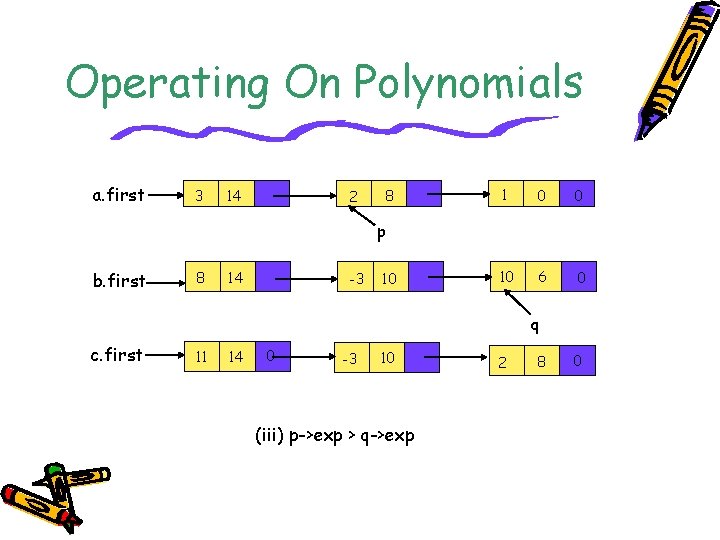
Operating On Polynomials a. first 3 14 2 8 1 0 0 10 6 0 p b. first 8 14 -3 10 q c. first 11 14 0 -3 10 (iii) p->exp > q->exp 2 8 0

Memory Leak • When polynomials are created for computation and then later on out of the program scope, all the memory occupied by these polynomials is supposed to return to system. But that is not the case. Since List. Node<Term> objects are not physically contained in List<Term> objects, the memory they occupy is lost to the program and is not returned to the system. This is called memory leak. • Memory leak will eventually occupy all system memory and causes system to crash. • To handle the memory leak problem, a destructor is needed to properly recycle the memory and return it back to the system.

List Destructor Template <class Type> List<Type>: : ~List() // Free all nodes in the chain { List. Node<Type>* next; for (; first = next) { next = first->link; delete first; } }

Free Pool • When items are created and deleted constantly, it is more efficient to have a circular list to contain all available items. • When an item is needed, the free pool is checked to see if there is any item available. If yes, then an item is retrieved and assigned for use. • If the list is empty, then either we stop allocating new items or use new to create more items for use.

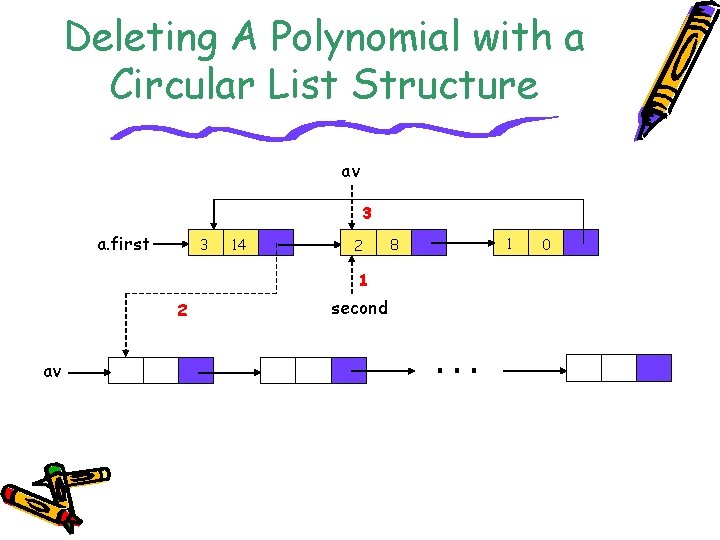
Using Circular Lists For Polynomials • By using circular lists for polynomials and free pool mechanism, the deleting of a polynomial can be done in a fixed amount of time independent of the number of terms in the polynomial.

Deleting A Polynomial with a Circular List Structure av 3 a. first 3 14 2 1 2 av second 8 1 0

Equivalence Class • For any polygon x, x ≡ x. Thus, ≡ is reflexive. • For any two polygons x and y, if x ≡ y, then y ≡ x. Thus, the relation ≡ is symetric. • For any three polygons x, y, and z, if x ≡ y and y ≡ z, then x ≡ z. The relation ≡ is transitive.

Equivalence Definition: A relation ≡ over a set S, is said to be an equivalence relation over S iff it is symmetric, reflexive, and transitive over S. Example: Supposed 12 polygons 0 ≡ 4, 3 ≡ 1, 6 ≡ 10, 8 ≡ 9, 7 ≡ 4, 6 ≡ 8, 3 ≡ 5, 2 ≡ 11, and 11 ≡ 0. Then they are partitioned into three equivalence classes: {0, 2, 4, 7, 11}; {1 , 3, 5}; {6, 8, 9 , 10}

Equivalence (Cont. ) • Two phases to determine equivalence – In the first phase the equivalence pairs (i, j) are read in and stored. – In phase two, we begin at 0 and find all pairs of the form (0, j). Continue until the entire equivalence class containing 0 has been found, marked, and printed. • Next find another object not yet output, and repeat the above process.

Equivalence Definition: A relation ≡ over a set S, is said to be an equivalence relation over S iff it is symmetric, reflexive, and transitive over S. Example: Supposed 12 polygons 0 ≡ 4, 3 ≡ 1, 6 ≡ 10, 8 ≡ 9, 7 ≡ 4, 6 ≡ 8, 3 ≡ 5, 2 ≡ 11, and 11 ≡ 0. Then they are partitioned into three equivalence classes: {0, 2, 4, 7, 11}; {1 , 3, 5}; {6, 8, 9 , 10}

Equivalence (Cont. ) • Two phases to determine equivalence – In the first phase the equivalence pairs (i, j) are read in and stored. – In phase two, we begin at 0 and find all pairs of the form (0, j). Continue until the entire equivalence class containing 0 has been found, marked, and printed. • Next find another object not yet output, and repeat the above process.

Equivalence Classes (Cont. ) • If a Boolean array pairs[n][n] is used to hold the input pairs, then it might waste a lot of space and its initialization requires complexity Θ(n 2). • The use of linked list is more efficient on the memory usage and has less complexity, Θ(m+n).

Linked List Representation [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10][11] data link 11 data link 4 0 3 0 11 0 5 7 1 0 0 0 3 0 8 10 0 4 0 6 9 0 8 0 6 0 0 2 0

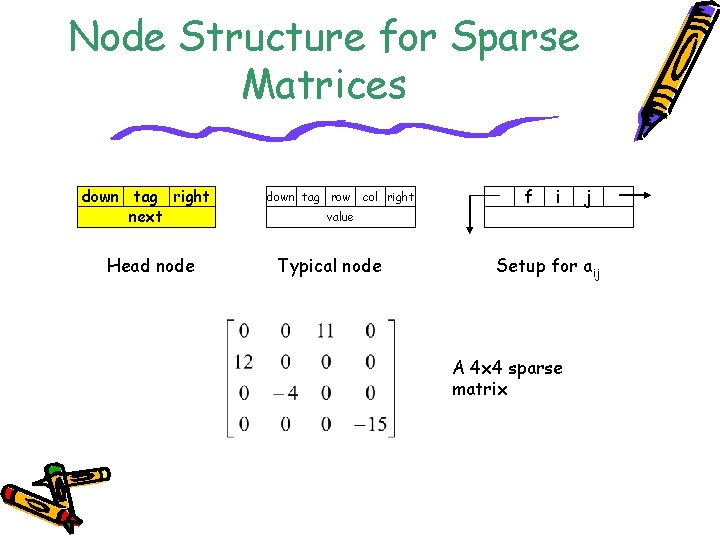
Linked List for Sparse Matrix • Sequential representation of sparse matrix suffered from the same inadequacies as the similar representation of Polynomial. • Circular linked list representation of a sparse matrix has two types of nodes: – head node: tag, down, right, and next – entry node: tag, down, row, col, right, value • Head node i is the head node for both row i and column i. • Each head node is belonged to three lists: a row list, a column list, and a head node list. • For an nxm sparse matrix with r nonzero terms, the number of nodes needed is max{n, m} + r + 1.

Node Structure for Sparse Matrices down tag right next Head node down tag row col right value Typical node f i j Setup for aij A 4 x 4 sparse matrix

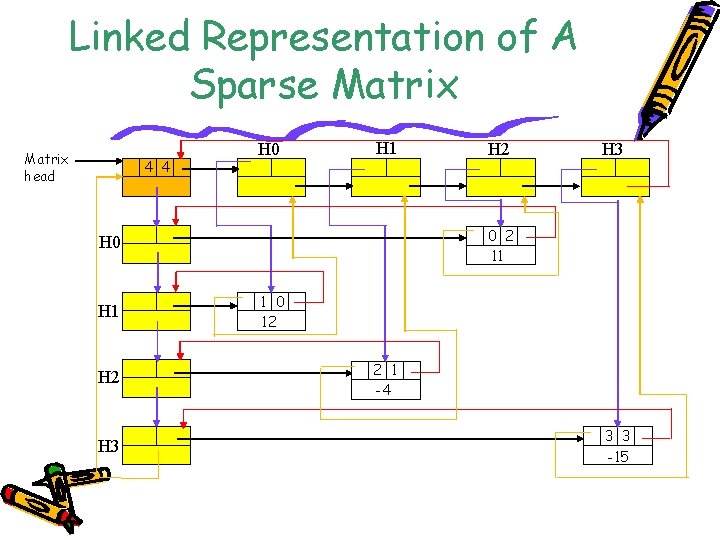
Linked Representation of A Sparse Matrix head 4 4 H 0 H 1 H 2 H 3 0 2 11 H 0 H 1 H 2 1 0 12 2 1 -4 3 3 -15

Reading In A Sparse Matrix • Assume the first line consists of the number of rows, the number of columns, and the number of nonzero terms. Then followed by num-terms lines of input, each of which is of the form: row, column, and value. • Initially, the next field of head node i is to keep track of the last node in column i. Then the column field of head nodes are linked together after all nodes has been read in.

Complexity Analysis • Input complexity: O(max{n, m} + r) = O(n + m + r) • Complexity of ~Maxtrix(): Since each node is in only one row list, it is sufficient to return all the row lists of a matrix. Each row is circularly linked, so they can be erased in a constant amount of time. The complexity is O(m+n).

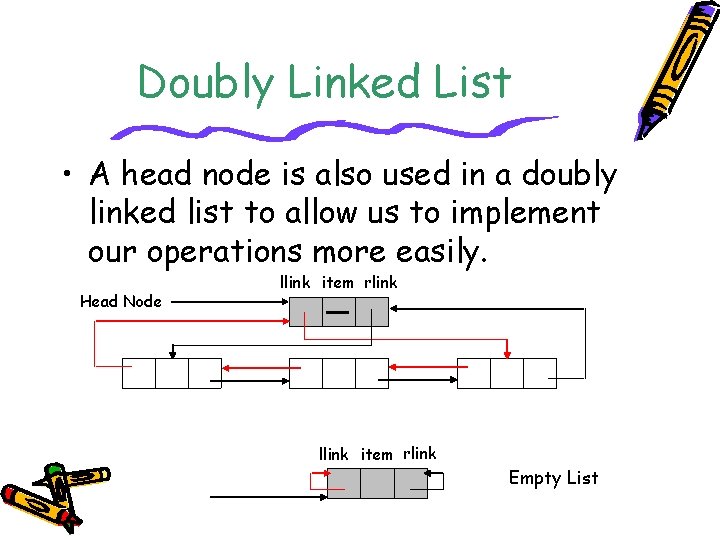
Doubly Linked Lists • The problem of a singly linked list is that supposed we want to find the node precedes a node ptr, we have to start from the beginning of the list and search until find the node whose link field contains ptr. • To efficiently delete a node, we need to know its preceding node. Therefore, doubly linked list is useful. • A node in a doubly linked list has at least three fields: left link field (llink), a data field (item), and a right link field (rlink).

Doubly Linked List • A head node is also used in a doubly linked list to allow us to implement our operations more easily. Head Node llink item rlink Empty List

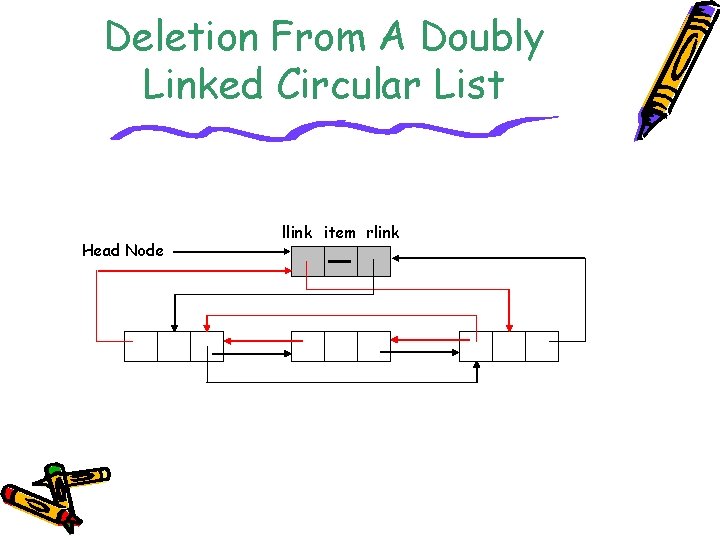
Deletion From A Doubly Linked Circular List Head Node llink item rlink

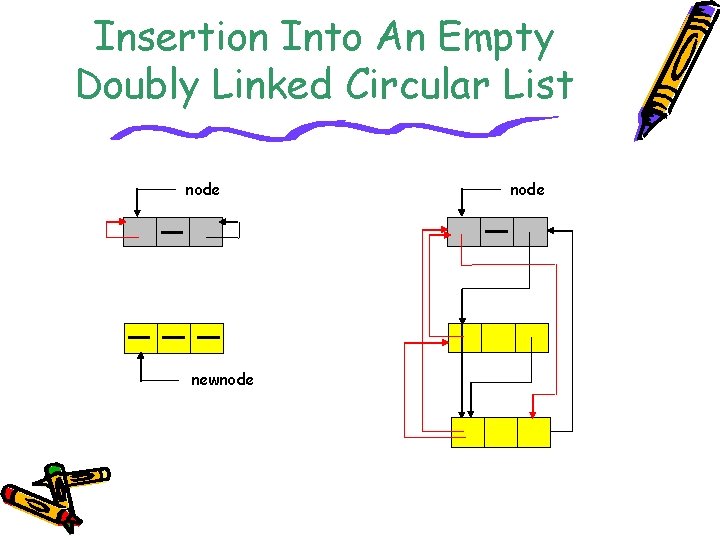
Insertion Into An Empty Doubly Linked Circular List node newnode

Generalized Lists • Definition: A generalized list, A, is a finite sequence of n ≥ 0 elements, α 0, α 1, α 2, …, αn-1, where αi, is either an atom or a list. The elements αi, 0≤ i ≤ n – 1, that are not atoms are said to be the sublists of A. • A list A is written as A = (α 0, …, αn-1 ), and the length of the list is n. • Conventionally, a capital letter is used to represent a list and a lower case letter is to represent an atom. • The α 0 is the head of list A and the rest (α 1, …, αn 1) is the tail of list A.

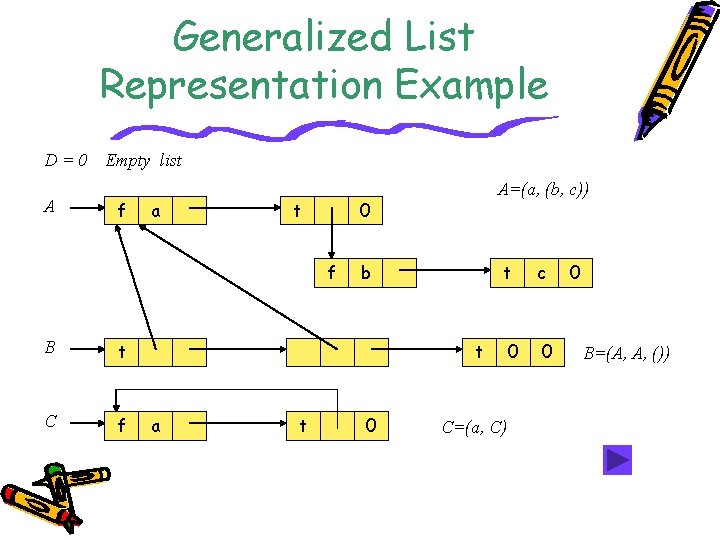
Generalized List Examples • D = ( ): the null, or empty, list; its length is zero. • A = (a, (b, c)): a list of length of two; its first element is the atom a, and its second element is the linear list (b, c). • B = (A, A, ( )): A list of length of three whose first two elements are the list A, and the third element is the null list D. • C = (a, C): is a recursive list of length two; C corresponds to the infinite list C = (a, (a, …))).

Generalized Lists • head(A) = ‘a’ and tail(A) = (b, c), head(tail(A) ) = (b, c) and tail(A)) = (). • Lists may be shared by other lists • Lists may be recursive.

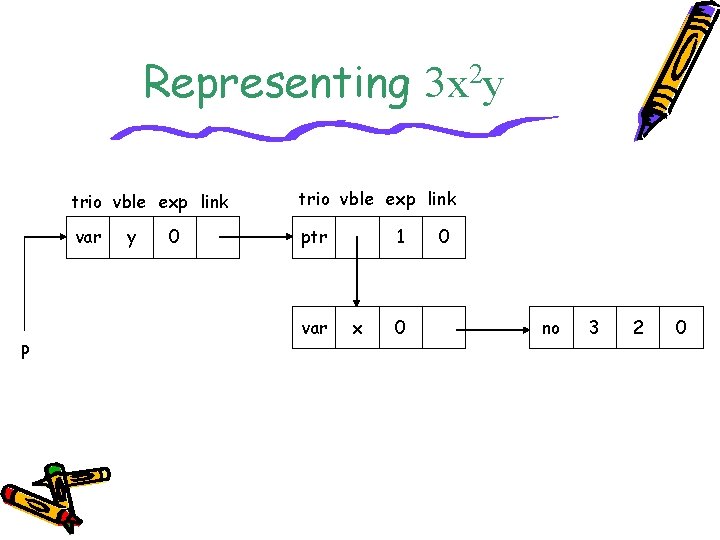
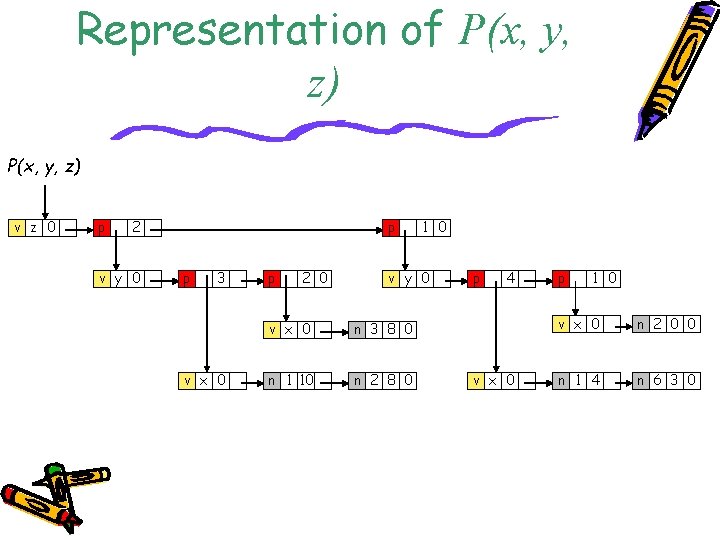
Generalized List Application Example • Consider the polynomial P(x, y, z) with various variables. It is obvious the sequential representation is not suitable to this. • What if a linear list is used? – The size of the node will vary in size, causing problems in storage management. • Let’s try the generalized list.

Generalized List Application Example • P(x, y, z) can be rewritten as follows: • The above can be written as Cz 2 + Dz. Both C and D are polynomials themselves but with variables x and y only. • If we look at polynomial C only, it is actually of the form Ey 3 + Fy 2, where E and F are polynomial of x only. • Continuing this way, every polynomial consists of a variable plus coefficient-exponent pairs. Each coefficient is itself a polynomial.

Poly. Node Class in C++ enum Triple{ var, ptr, no }; class Poly. Node { Poly. Node *link; int exp; Triple trio; union { char vble; Poly. Node *dlink; int coef; }; };

Poly. Node in C++ (Cont. ) • trio == var: the node is a head node. – vble indicates the name of the variable. Or it is an integer point to the variable in a variable table. – exp is set to 0. • trio == ptr: coefficient itself is a list and is pointed by the field dlink. exp is the exponent of the variable on which the list is based on. • trio == no, coefficient is an integer and is stored in coef. exp is the exponent of the variable on which the list is based on.

Representing P 2 3 x y trio vble exp link var ptr y 0 var 1 x 0 0 no 3 2 0

Representation of P(x, y, z) v z 0 p 2 v y 0 p p 3 v x 0 p 2 0 1 0 v y 0 v x 0 n 3 8 0 n 1 10 n 2 8 0 p 4 v x 0 p 1 0 v x 0 n 2 0 0 n 1 4 n 6 3 0

Recursive Algorithms For Lists • A recursive algorithm consists of two components: – The recursive function (the workhorse); declared as a private function – A second function that invokes the recursive function at the top level (the driver); declared as a public function.

Program 4. 6 Copying A List // Driver void Gen. List: : Copy(const Gen. List& l) { first = Copy(l. first); } // Workhorse Gen. List. Node* Gen. List: : Copy(Gen. List. Node *p) // Copy the nonrecursive list with no shared sublists pointed at by p { Gen. List. Node *q = 0; if (p) { q = new Gen. List. Node; q->tag = p->tag; if (!p->tag) q->data = p->data; else q->dlink = Copy(p->dlink); q->link = Copy(p->link); } return q; }

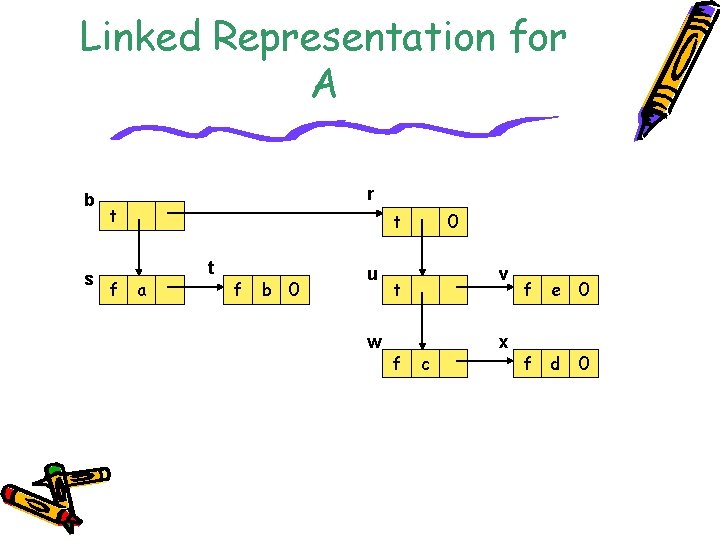
Linked Representation for A b s r t f t a t f b 0 u w 0 v t f c x f e 0 f d 0

Generalized List Representation Example D=0 A Empty list f a t 0 f B t C f A=(a, (b, c)) b t c 0 0 t a t 0 C=(a, C) 0 B=(A, A, ())

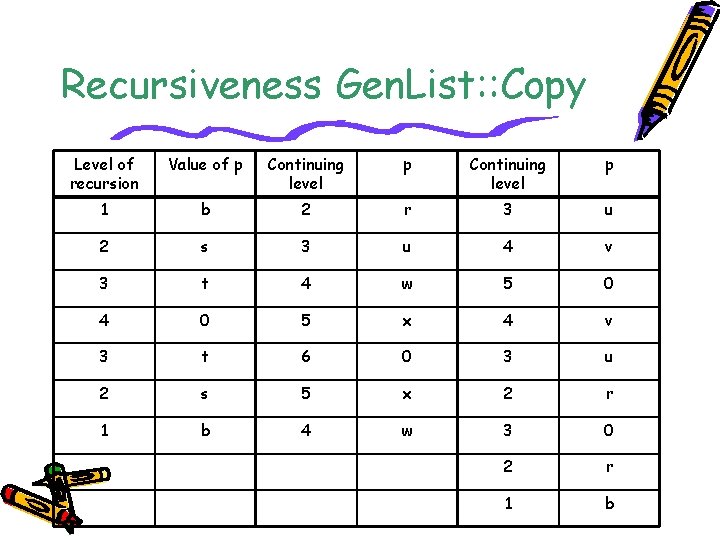
Recursiveness Gen. List: : Copy Level of recursion Value of p Continuing level p 1 b 2 r 3 u 2 s 3 u 4 v 3 t 4 w 5 0 4 0 5 x 4 v 3 t 6 0 3 u 2 s 5 x 2 r 1 b 4 w 3 0 2 r 1 b

Important List Functions • List Equality (Program 4. 37) • List Depth (Program 4. 38) – An empty list has depth 0.

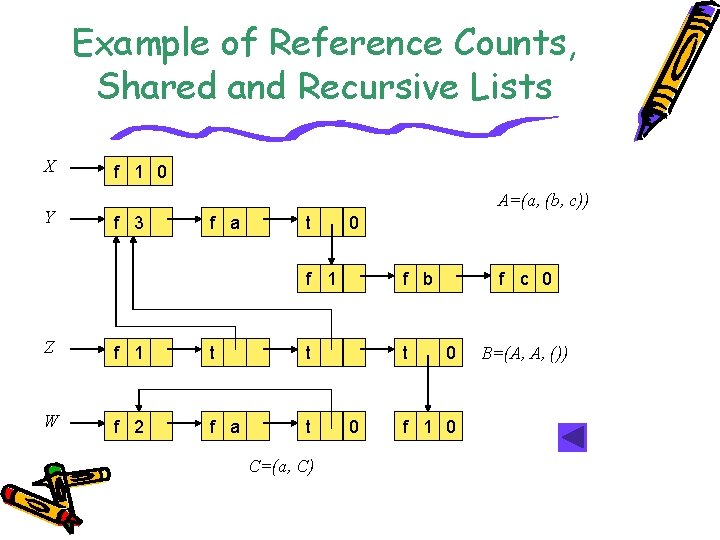
Reference Counts, Shared and Recursive Lists • Lists may be shared by other lists for the purpose of space saving. • Lists that are shared by other lists create problems when performing add or delete functions. For example, let’s look at the previous A, B, C, D example. When deleting the front node of list A would requires List B to update its pointers. • The use of the data field of a head node to record the reference count can resolve the aforementioned problem. The list can not be deleted unless the reference count is 0.

Example of Reference Counts, Shared and Recursive Lists X Y f 1 0 A=(a, (b, c)) f 3 f a t 0 f 1 f b t Z f 1 t t W f 2 f a t C=(a, C) 0 f c 0 0 f 1 0 B=(A, A, ())

Erasing A List Recursively // Driver Gen. List: : ~Gen. List() // Each head node has a reference count. We assume first ≠ 0. { Delete(first); first = 0; } // Workhorse void Gen. List: : Delete(Gen. List. Node* x) { x->ref--; // decrement reference coutn of head node. if (!x->ref) { Gen. List. Node *y = x; // y traverses top-level of x. while (y->link) { y= y->link; if (y->tag == 1) Delete (y->dlink); } y->link = av; // Attach top-level nodes to av list av = x; } }

Issue In Erasing Recursive Lists • When erasing a recursive list (either direct recursive or indirect recursive), the reference count does not become 0. Then the nodes are not returned to available list. This will cause memory leak issue.

Virtual Functions and Dynamic Binding in C++ • A pointer to a derived class type is implicitly converted to a pointer to its base class; similar to the reference. – E. g. , Rectangle r; // instance of derived class Polygon *s = &r; // Assign rectangle to polygon

Virtual Functions and Dynamic Binding in C++ • What happen if a member function is designed for rectangle and we call this function on object s? – The implementation for the Polygon would be used. – Virtual functions in C++ is designed to resolve this issue. – A virtual function is dynamically bound - that is, the operation corresponding to the dynamic type of the object that invoked it, is used.

Virtual Member Functions • Virtual member functions: – A member function of a base class is virtual if its prototype in its class definition is preceded by the keyword virtual. If a virtual function, whose implementation is redefined in a derived class, is invoked by a base class object, then the implementation corresponding to the current dynamic type of that base object is used. – If the implementation of a virtual function is not redefined, then the implementation of the virtual function in the base class is used. Rectangle r; : // assume r is initialized at this point Polygon *s = &r; s->Concave(); // returns FALSE

Non-Virtual Member Functions • Functions that do not have the key word virtual precedes them in the base class is called non-virtual member function. Usually, they should not be redefined in derived class.

Pure Virtual Functions • A virtual member function is said to be pure if it is implemented by its class. It is assigned the value 0 to indicate that it is pure. – If a base class contains one or more pure virtual functions, it is called an abstract class. • You are not allowed to create instances of the abstract base class. Polygon p; Polygon *p; // illegal // legal • Pure virtual functions must be redefined in the derived class. • A pure virtual function is used when it is obvious that a case class must support a particular function that only a derived class can provide. For example, the function perimeter() for polygon class.

Heterogeneous Lists • A heterogeneous list is one that contains nodes of different types. – If merging nodes by using union, then each node is allocated for the largest node type. This would waste space. – Use of public inheritance and virtual functions can resolve this issue.

Using union To Implement A List of Mixed Nodes struct Data { int id; // id = 0, 1, or 2 if the node contains a char, an int, or a float union { int i; char c; float f; }; }; class Combined. Node // Use union to merge different node types into one class definition { friend class List; friend class List. Iterator; private: Data data; Space allocation is Combined. Node *link; based on the largest }; data type, which is float.

Using union To Implement A List of Mixed Nodes (Cont. ) class list { friend class List. Iterator; public: // List manipulation operations follow. private: Combined. Node *first; }; // the return type of class List. Iterator is Data*

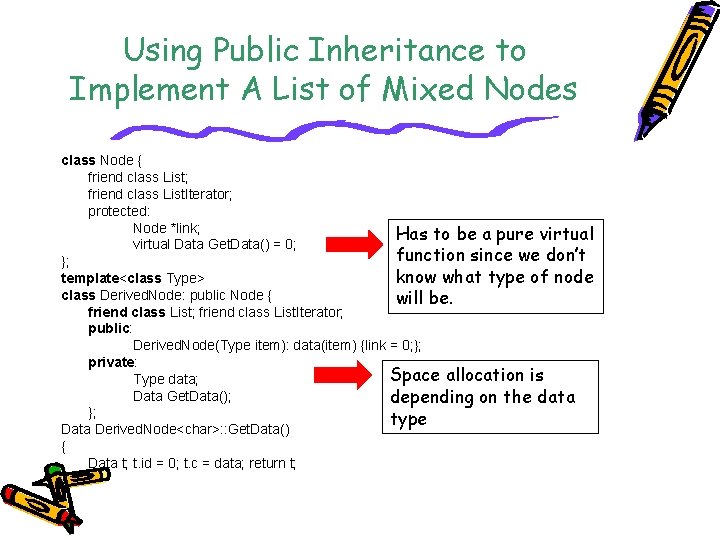
Using Public Inheritance to Implement A List of Mixed Nodes class Node { friend class List; friend class List. Iterator; protected: Node *link; Has to be a pure virtual Data Get. Data() = 0; function since we don’t }; know what type of node template<class Type> class Derived. Node: public Node { will be. friend class List; friend class List. Iterator; public: Derived. Node(Type item): data(item) {link = 0; }; private: Space allocation is Type data; Data Get. Data(); depending on the data }; type Data Derived. Node<char>: : Get. Data() { Data t; t. id = 0; t. c = data; return t; }

Using Public Inheritance to Implement A List of Mixed Nodes (Cont. ) class List { friend class List. Iterator; public: Node *first; }; class List. Iterator { public: List. Iterator(const List & l); list(l), current(l. first){ }; Data* First(); // minor change in homogeneous list implementation Data* Next(); // minor change in homogeneous list implementation Boolean Not. Null(); // implemented as for homogeneous lists Boolean Next. Not. Null(); // implemented as for homogeneous lists private: const List& list; Node* current; Data temp; }; Data* List. Iterator: : First() { if(list. first) { temp = list. first->Get. Data(); // use Get. Data to retrieve element return &temp; } return 0; };

Key Point of Using Dynamic Typing and Public Inheritance • Key point: using the dynamic typing through public inheritance, a pointer to a Node* may be used to point to nodes of type Derived. Node<char>, Derived. Node<int>, and Derived. Node<float>. This elements the problem that necessitated the artificial union of the different node types.