Review of graphing inequalities 1 start by graphing
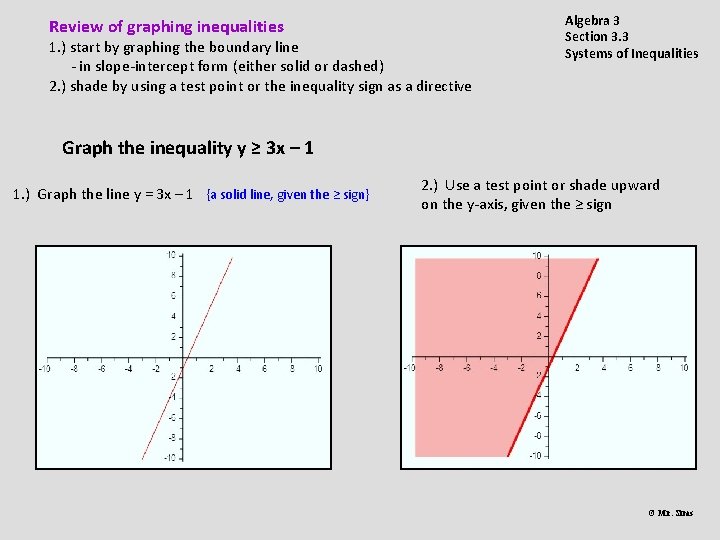
Review of graphing inequalities 1. ) start by graphing the boundary line - in slope-intercept form (either solid or dashed) 2. ) shade by using a test point or the inequality sign as a directive Algebra 3 Section 3. 3 Systems of Inequalities Graph the inequality y ≥ 3 x – 1 1. ) Graph the line y = 3 x – 1 {a solid line, given the ≥ sign} 2. ) Use a test point or shade upward on the y-axis, given the ≥ sign © Mr. Sims
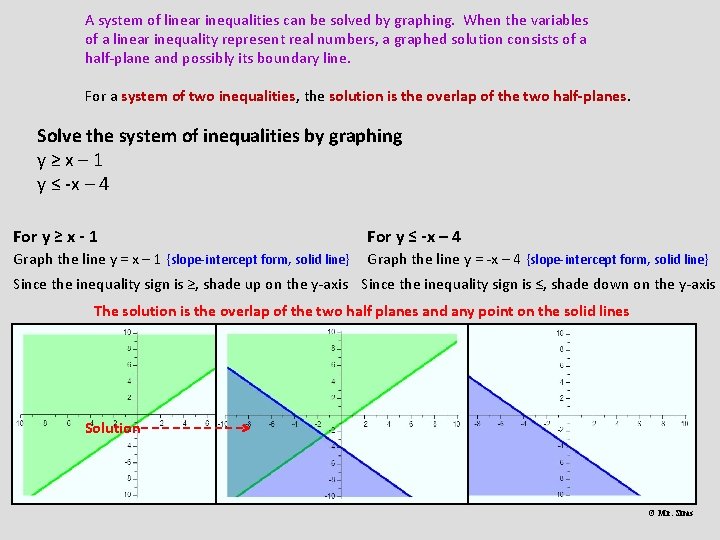
A system of linear inequalities can be solved by graphing. When the variables of a linear inequality represent real numbers, a graphed solution consists of a half-plane and possibly its boundary line. For a system of two inequalities, the solution is the overlap of the two half-planes. Solve the system of inequalities by graphing y≥x– 1 y ≤ -x – 4 For y ≥ x - 1 For y ≤ -x – 4 Graph the line y = x – 1 {slope-intercept form, solid line} Graph the line y = -x – 4 {slope-intercept form, solid line} Since the inequality sign is ≥, shade up on the y-axis Since the inequality sign is ≤, shade down on the y-axis The solution is the overlap of the two half planes and any point on the solid lines Solution © Mr. Sims
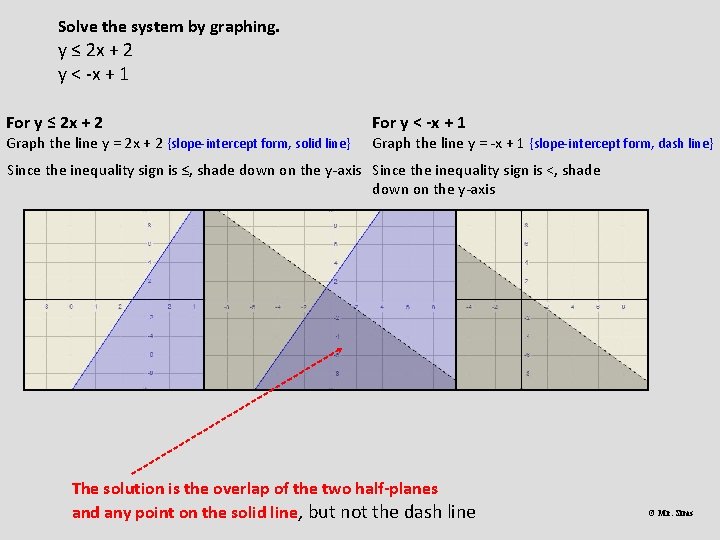
Solve the system by graphing. y ≤ 2 x + 2 y < -x + 1 For y ≤ 2 x + 2 Graph the line y = 2 x + 2 {slope-intercept form, solid line} For y < -x + 1 Graph the line y = -x + 1 {slope-intercept form, dash line} Since the inequality sign is ≤, shade down on the y-axis Since the inequality sign is <, shade down on the y-axis The solution is the overlap of the two half-planes and any point on the solid line, but not the dash line © Mr. Sims
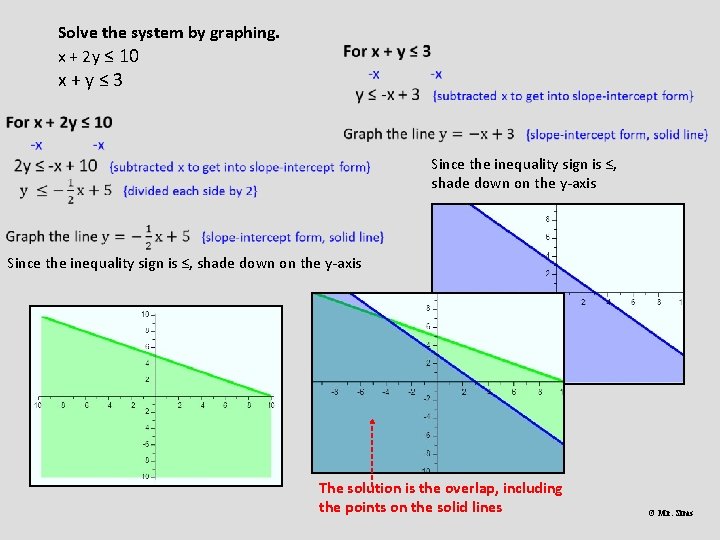
Solve the system by graphing. x + 2 y ≤ 10 x+y≤ 3 Since the inequality sign is ≤, shade down on the y-axis The solution is the overlap, including the points on the solid lines © Mr. Sims
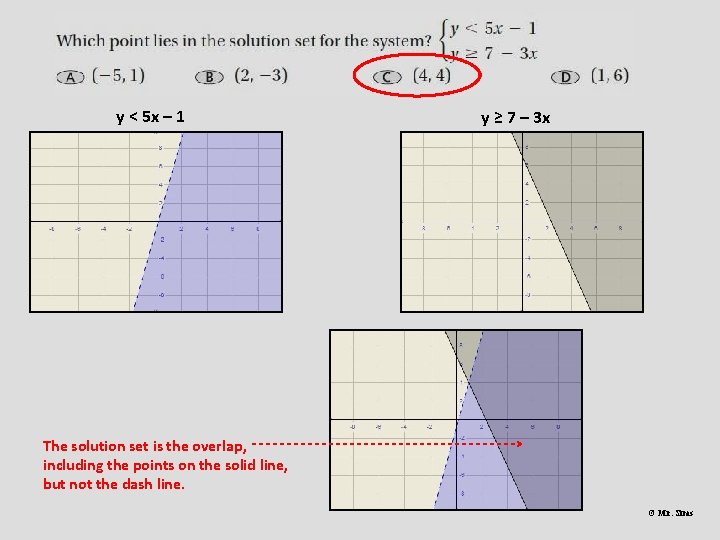
y < 5 x – 1 y ≥ 7 – 3 x The solution set is the overlap, including the points on the solid line, but not the dash line. © Mr. Sims

Any rebroadcast, reproduction, modification or other use of the work, presentations, and materials from this site without the express written consent of Mr. Sims, is prohibited. © Mr. Sims. All rights reserved. © Mr. Sims
- Slides: 6