Review of Functions Domain Range Function Relation Vertical






- Slides: 24

Review of Functions Domain, Range, Function, Relation, Vertical Line Test

A relation is any set of ordered pairs.

The ordered pair for B is (3, -2).

A function is a set of ordered pairs where each input value has only one output value. Why does the second table NOT show a function?

A function is a set of ordered pairs where each input value has only one output value. There are two outputs for the input value 4.

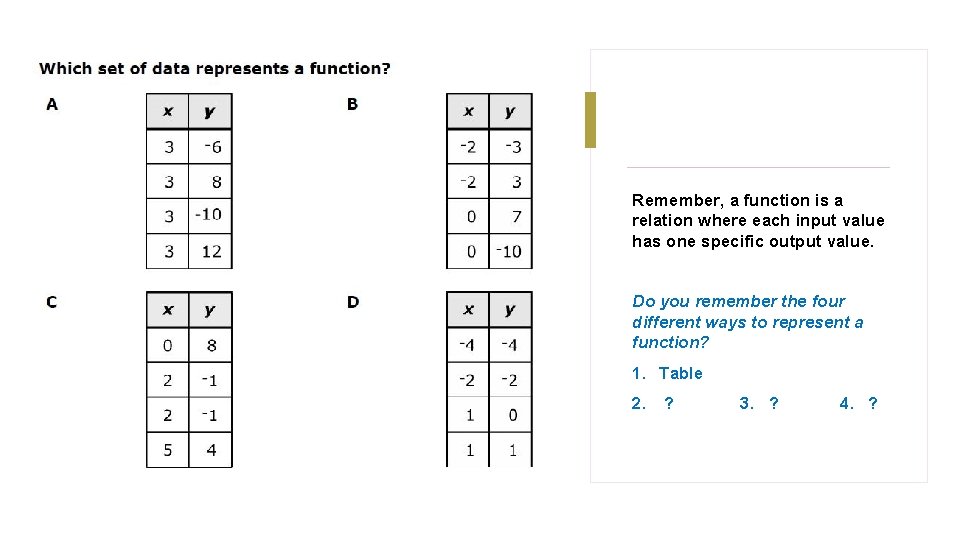
Remember, a function is a relation where each input value has one specific output value. Do you remember the four different ways to represent a function? 1. Table 2. ? 3. ? 4. ?

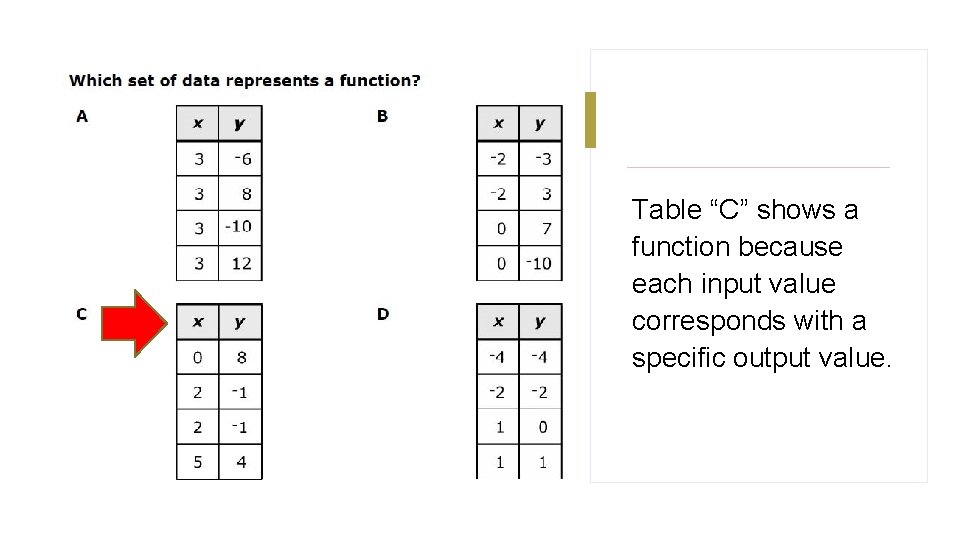
Table “C” shows a function because each input value corresponds with a specific output value.

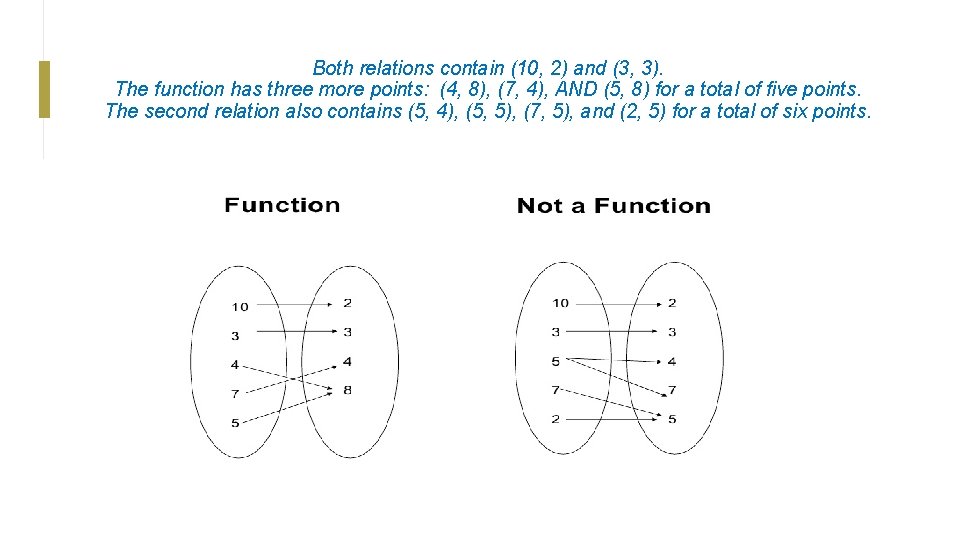
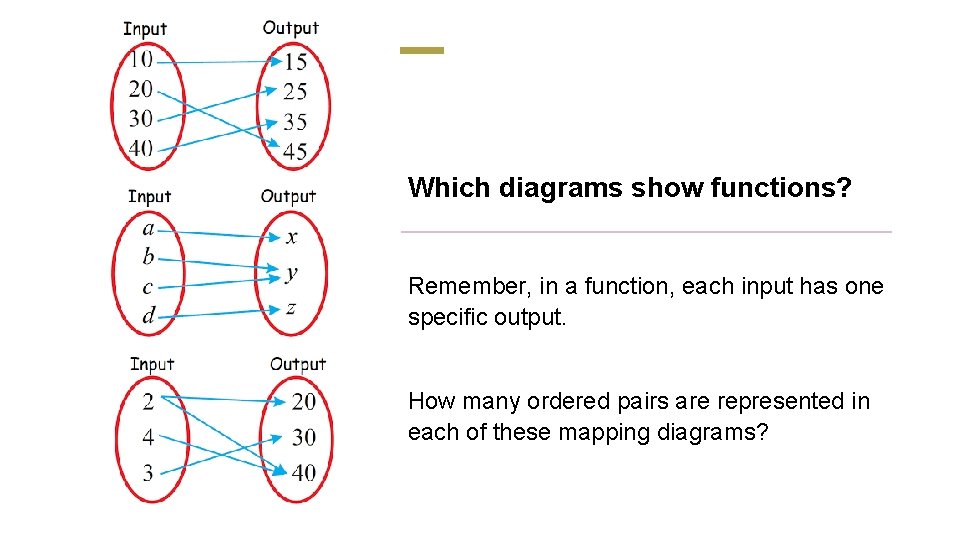
Relations can be shown as mapping diagrams. How many ordered pairs are in each relation?

Both relations contain (10, 2) and (3, 3). The function has three more points: (4, 8), (7, 4), AND (5, 8) for a total of five points. The second relation also contains (5, 4), (5, 5), (7, 5), and (2, 5) for a total of six points.

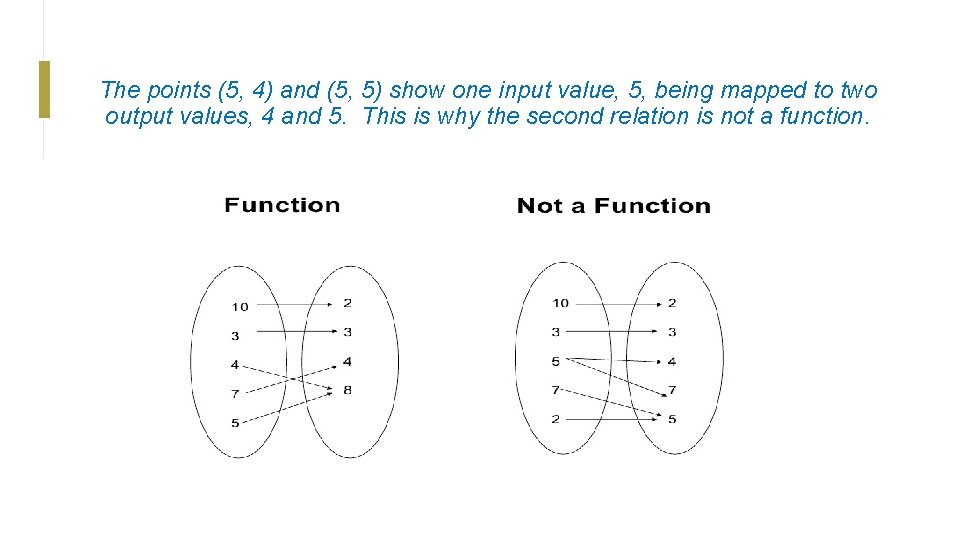
The points (5, 4) and (5, 5) show one input value, 5, being mapped to two output values, 4 and 5. This is why the second relation is not a function.

Which diagrams show functions? Remember, in a function, each input has one specific output. How many ordered pairs are represented in each of these mapping diagrams?

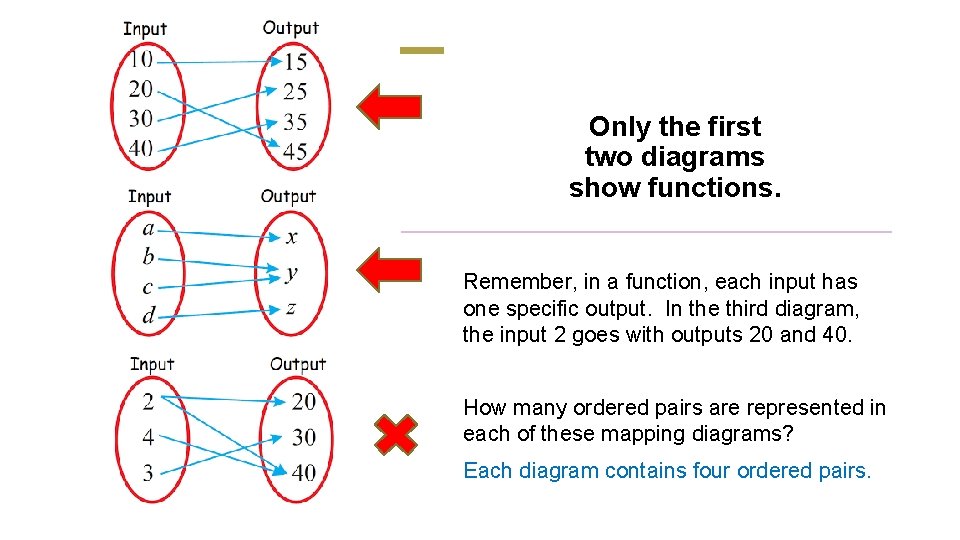
Only the first two diagrams show functions. Remember, in a function, each input has one specific output. In the third diagram, the input 2 goes with outputs 20 and 40. How many ordered pairs are represented in each of these mapping diagrams? Each diagram contains four ordered pairs.

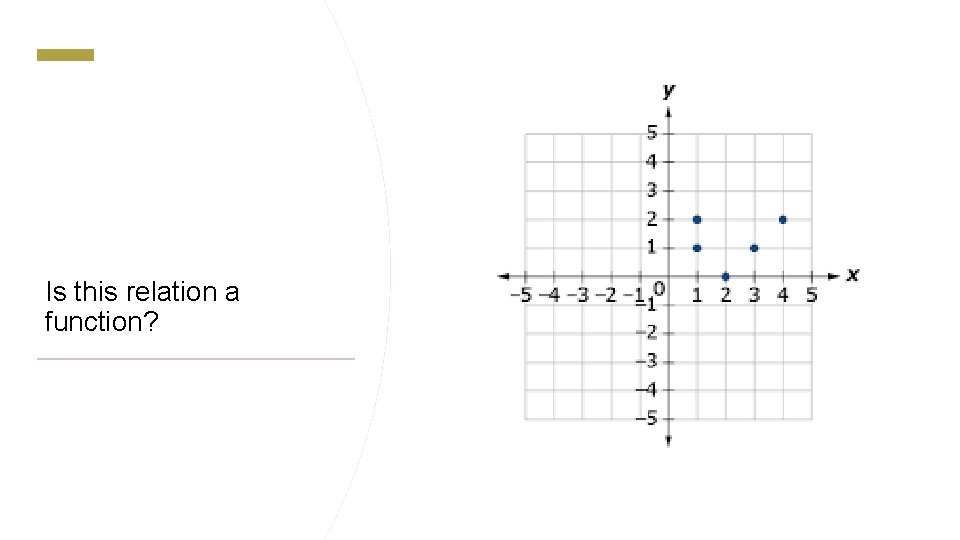
Is this relation a function?

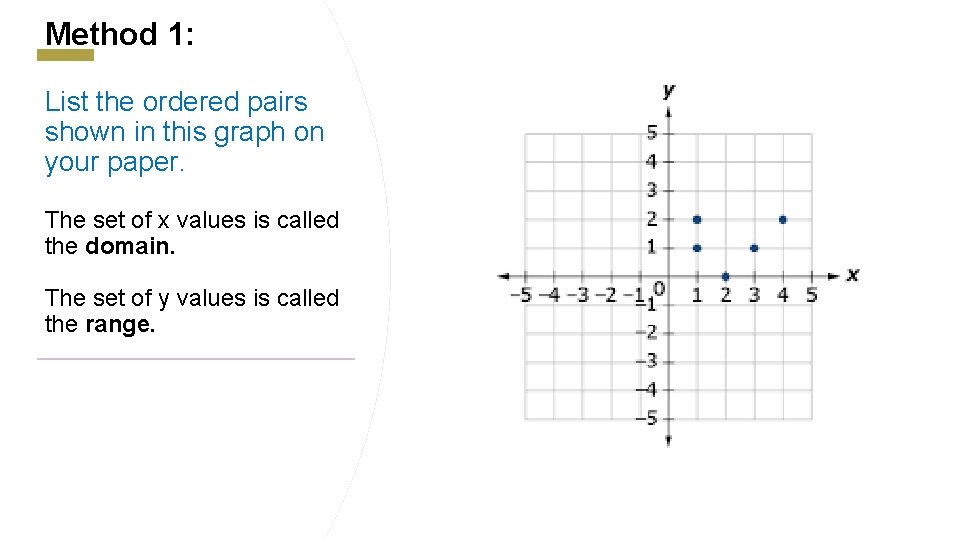
Method 1: List the ordered pairs shown in this graph on your paper. The set of x values is called the domain. The set of y values is called the range.

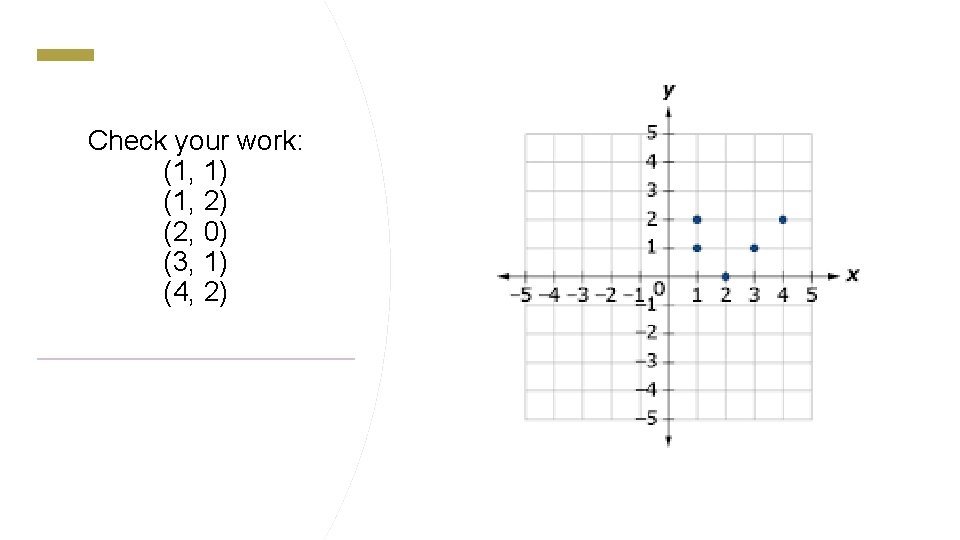
Check your work: (1, 1) (1, 2) (2, 0) (3, 1) (4, 2)

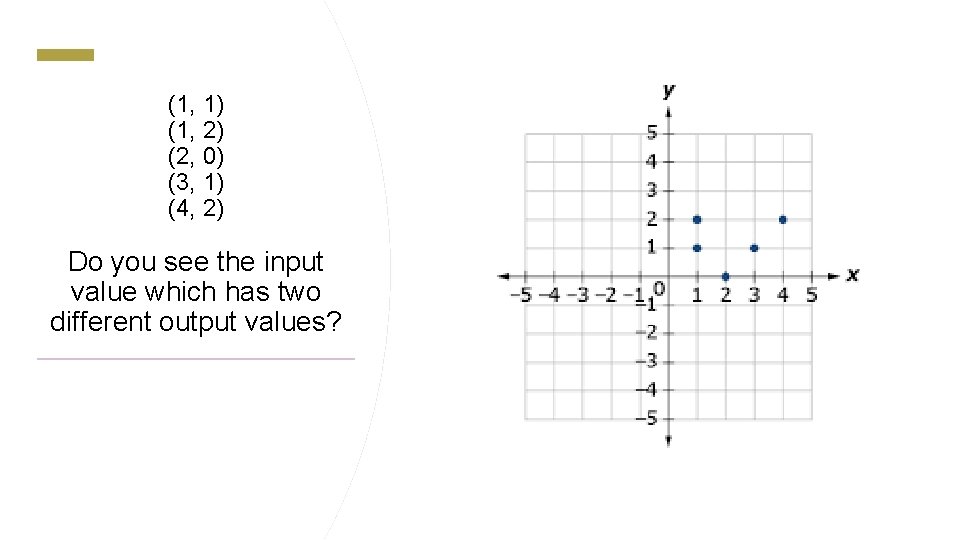
(1, 1) (1, 2) (2, 0) (3, 1) (4, 2) Do you see the input value which has two different output values?

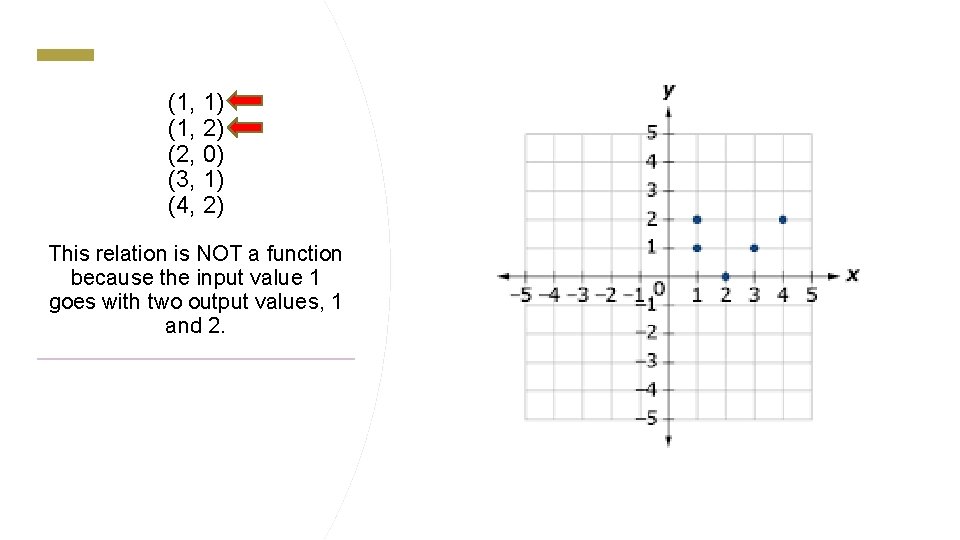
(1, 1) (1, 2) (2, 0) (3, 1) (4, 2) This relation is NOT a function because the input value 1 goes with two output values, 1 and 2.

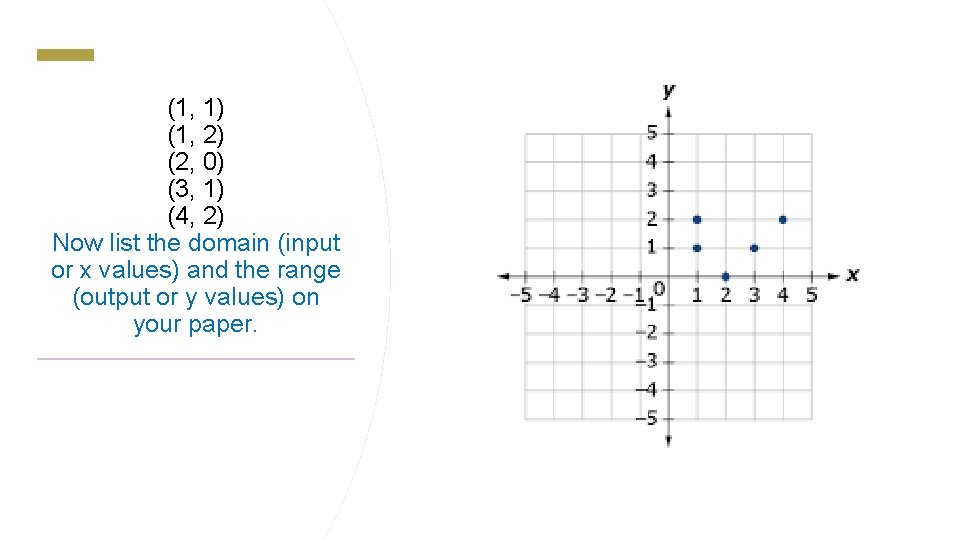
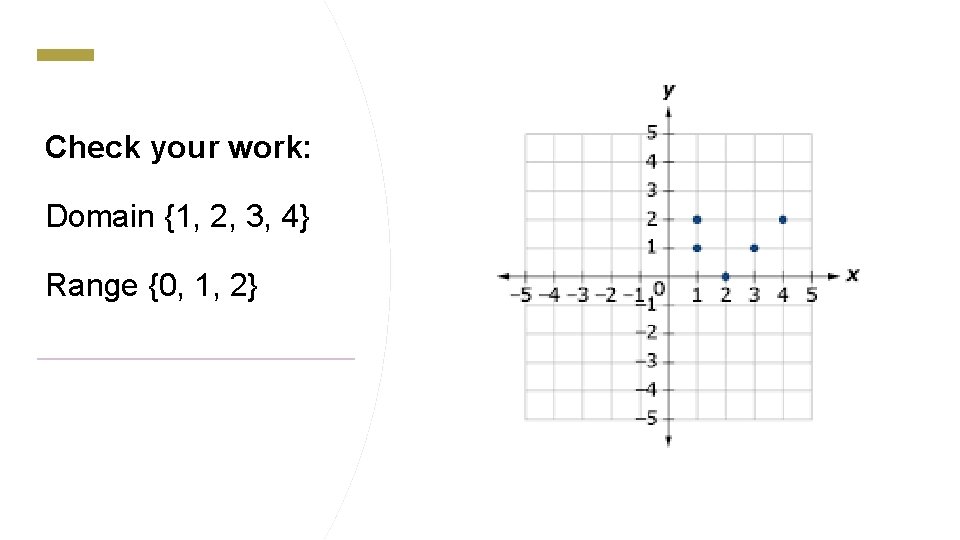
(1, 1) (1, 2) (2, 0) (3, 1) (4, 2) Now list the domain (input or x values) and the range (output or y values) on your paper.

Check your work: Domain {1, 2, 3, 4} Range {0, 1, 2}


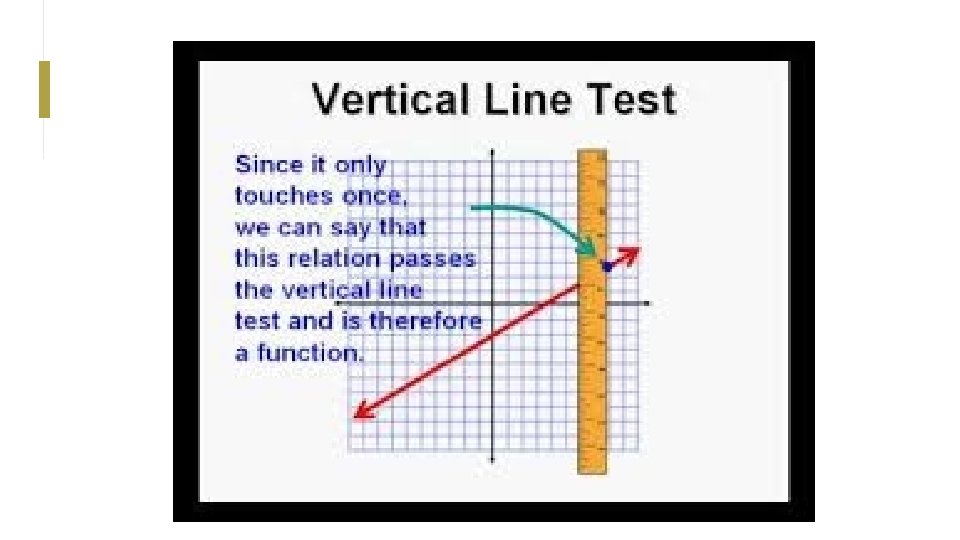
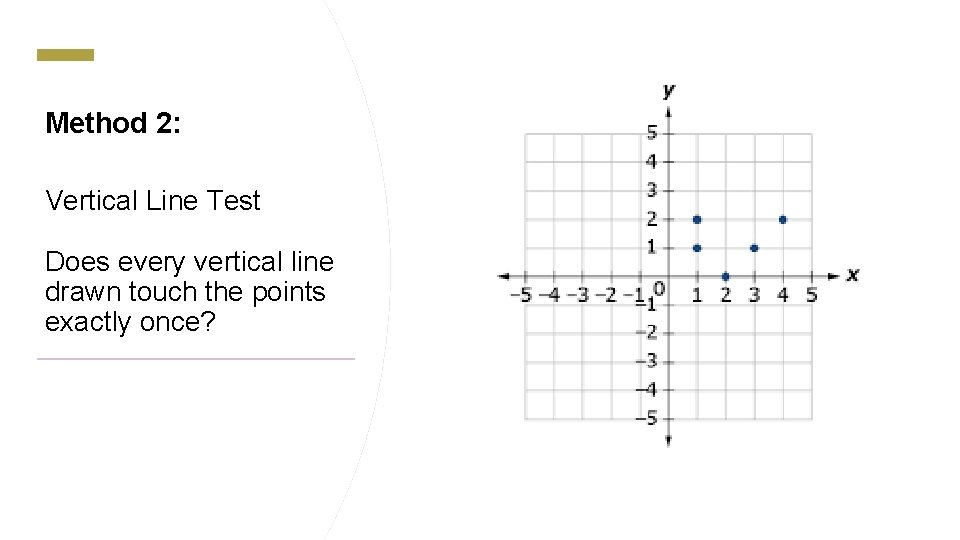
Method 2: Vertical Line Test Does every vertical line drawn touch the points exactly once?

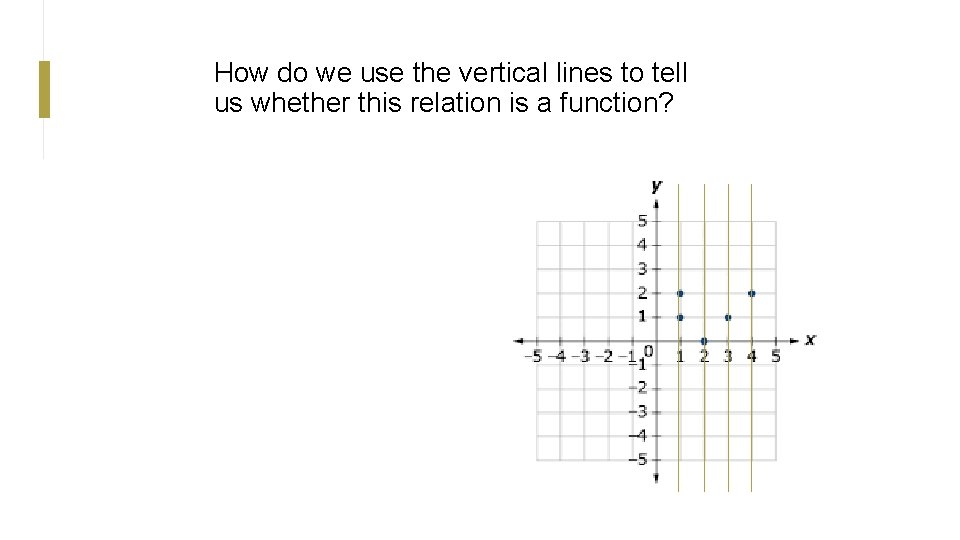
How do we use the vertical lines to tell us whether this relation is a function?

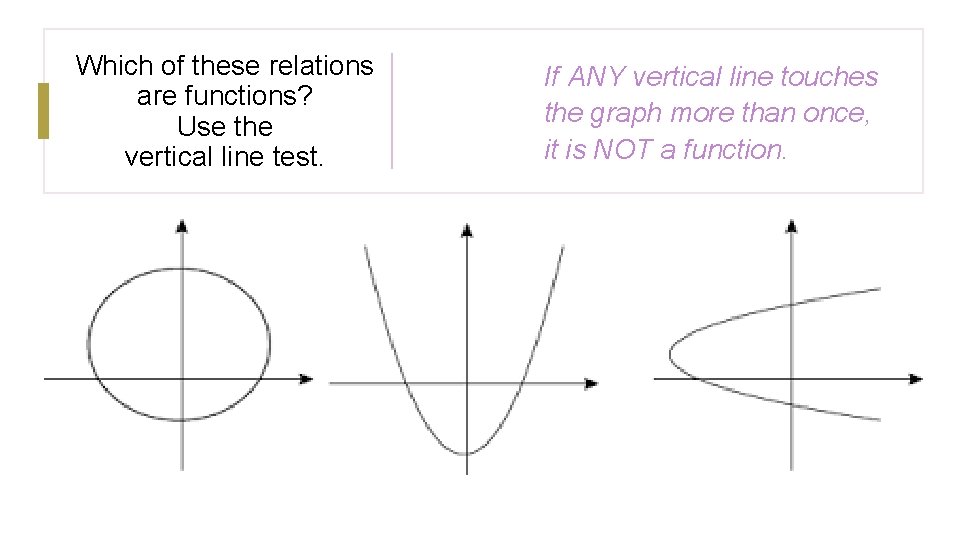
Which of these relations are functions? Use the vertical line test. If ANY vertical line touches the graph more than once, it is NOT a function.

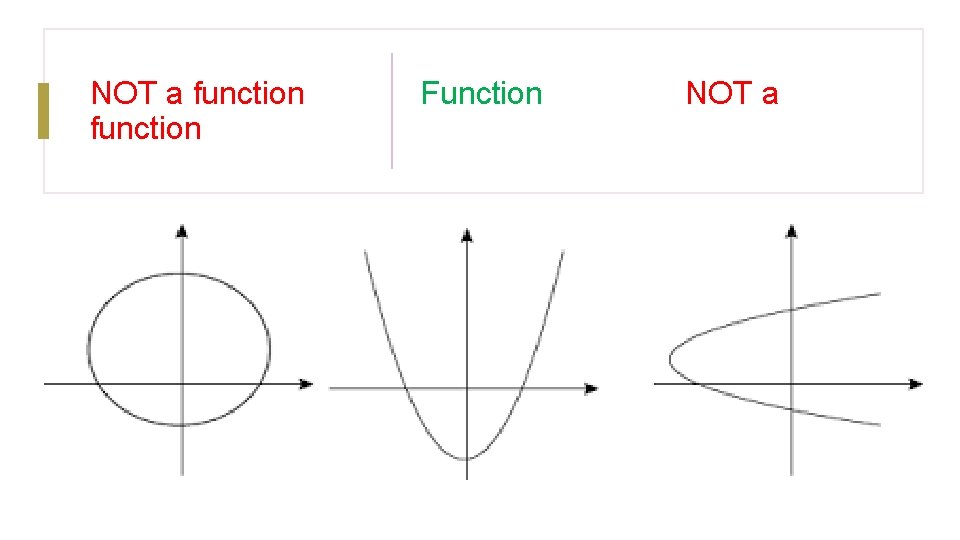
NOT a function Function NOT a