Review of DSP 1 Signal and Systems n

Review of DSP 1

Signal and Systems: n Signal are represented mathematically as functions of one or more independent variables. n Digital signal processing deals with the transformation of signal that are discrete in both amplitude and time. n Discrete time signal are represented mathematically as sequence of numbers. 2

Signals and Systems: n A discrete time system is defined mathematically as a transformation or operator. ¨ y[n] = T{ x[n] } x [n] T{. } y [n] 3

Linear Systems: n The class of linear systems is defined by the principle of superposition. n And n Where a is the arbitrary constant. ¨ The first property is called the additivity property and the second is called the homogeneity or scaling property. 4

Linear Systems: n These two property can be combined into the principle of superposition, H Linear System H H 5

Time-Invariant Systems: n A Time-Invariant system is a system for which a time shift or delay of the input sequence cause a corresponding shift in the output sequence. H H 6

LTI Systems: n n A particular important class of systems consists of those that are linear and time invariant. LTI systems can be completely characterized by their impulse response. n From principle of superposition: n Property of TI: 7

LTI Systems (Convolution): n Above equation commonly called convolution sum and represented by the notation 8

Convolution properties: n Commutativity: n Associativity: n Distributivity: n Time reversal: 9

…Convolution properties: n If two systems are cascaded, H 1 H 2 ¨ The overall impulse response of the combined system is the convolution of the individual IR: ¨ The overall IR is independent of the order: H 2 H 1 10

Duration of IR: n Infinite-duration impulse-response (IIR). n Finite-duration impulse-response (FIR) n In this case the IR can be read from the right-hand side of: 11

Transforms: Transforms are a powerful tool for simplifying the analysis of signals and of linear systems. n Interesting transforms for us: n ¨ Linearity applies: ¨ Convolution is replaced by simpler operation: 12

…Transforms: n Most commonly transforms that used in communications engineering are: ¨ Laplace transforms (Continuous in Time & Frequency) ¨ Continuous ¨ Discrete ¨Z Fourier transforms (Continuous in Time) Fourier transforms (Discrete in Time) 13

The Z Transform: n Definition Equations: ¨ Direct Z transform ¨ The Region Of Convergence (ROC) plays an essential role. 14

The Z Transform n (Elementary functions) : Elementary functions and their Z-transforms: ¨ Unit impulse: ¨ Delayed unit impulse: 15

The Z Transform ¨ Unit (…Elementary functions) : Step: ¨ Exponential: 16

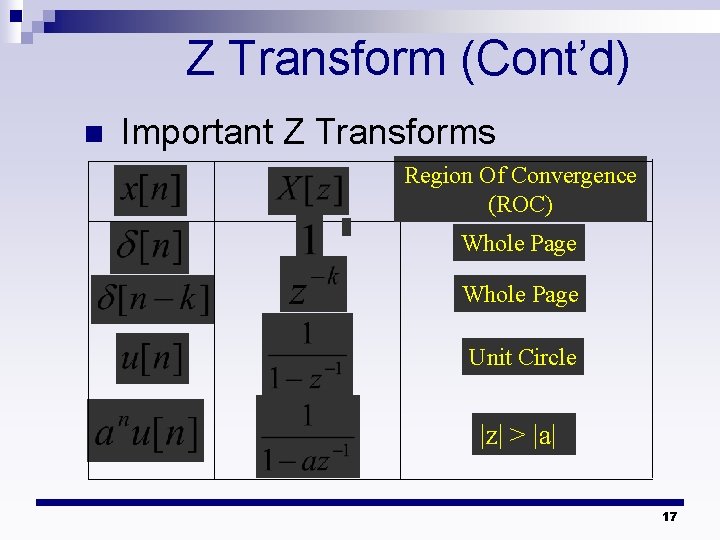
Z Transform (Cont’d) n Important Z Transforms Region Of Convergence (ROC) Whole Page Unit Circle |z| > |a| 17

The Z Transform n (Elementary properties) : Elementary properties of the Z transforms: ¨ Linearity: ¨ Convolution: if , Then 18

The Z Transform (…Elementary properties) : ¨ Shifting: ¨ Differences: n Forward differences of a function, n Backward differences of a function, 19

The Z Transform (…Region Of Convergence for Z transform) : ¨ Since the shifting theorem 20

The Z Transform (Region Of Convergence for Z transform) : n The ROC is a ring or disk in the z-plane centered at the origin : i. e. , n The Fourier transform of x[n] converges at absolutely if and only if the ROC of the ztransform of x[n] includes the unit circle. n The ROC can not contain any poles. 21

The Z Transform (…Region Of Convergence for Z transform) : n If x[n] is a finite-duration sequence, then the ROC is the entire z-plane, except possibly or. n If x[n] is a right-sided sequence, the ROC extends outward from the outermost finite pole in to. n The ROC must be a connected region. 22

The Z Transform (…Region Of Convergence for Z transform) : n A two-sided sequence is an infinite-duration sequence that is neither right sided nor left sided. n If x[n] is a two-sided sequence, the ROC will consist of a ring in the z-plane, bounded on the interior and exterior by a pole and not containing any poles. n If x[n] is a left-sided sequence, the ROC extends in ward from the innermost nonzero pole in to. 23

The Z Transform n n (Application to LTI systems) : We have seen that n By the convolution property of the Z transform n Where H(z) is the transfer function of system. Stability ¨A system is stable if a bounded input produced a bounded output, and a LTI system is stable if: 24

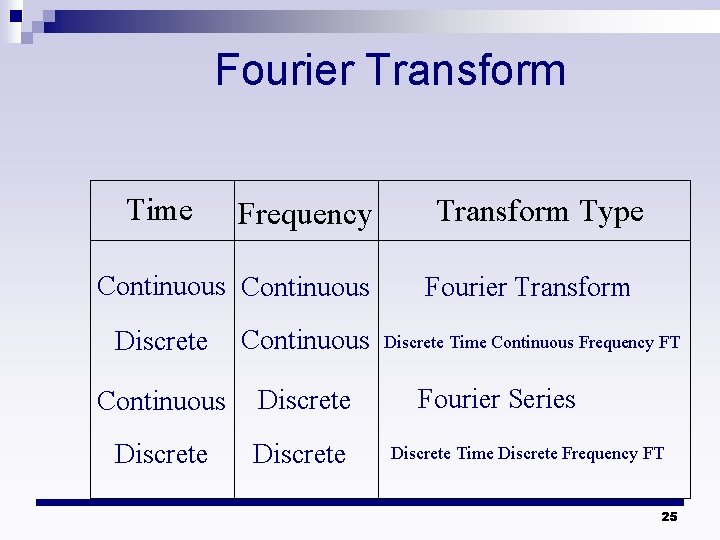
Fourier Transform Time Frequency Continuous Discrete Transform Type Fourier Transform Discrete Time Continuous Frequency FT Fourier Series Discrete Time Discrete Frequency FT 25

The Discrete Fourier Transform (DFT) n Discrete Fourier transform ¨ It is customary to use the ¨ Then the direct form is: 26

The Discrete Fourier Transform (DFT) ¨ With the same notation the inverse DFT is 27

The DFT (Elementary functions): n Elementary functions and their DFT: ¨ Unit impulse: ¨ Shifted unit impulse: 28

The DFT (…Elementary functions): ¨ Constant: ¨ Complex exponential: 29

The DFT (…Elementary functions): ¨ Cosine function: 30

The DFT n (Elementary properties) : Elementary properties of the DFT: ¨ Symmetry: If , Then ¨ Linearity: if and , Then 31

The DFT (…Elementary properties) : ¨ Shifting: because of the cyclic nature of DFT domains, shifting becomes a rotation. if , Then ¨ Time reversal: if , Then 32

The DFT (…Elementary properties) : ¨ Cyclic convolution: convolution is a shift, multiply and add operation. Since all shifts in the DFT are circular, convolution is defined with this circularity included. 33