Review of Components Analysis Aerospace Engineering International School

Review of Components Analysis Aerospace Engineering, International School of Engineering (ISE) Academic year : 2012 -2013 (August – December, 2012) Jeerasak Pitakarnnop , Ph. D. Jeerasak. p@chula. ac. th jeerasak@nimt. or. th November 17, 2012 Aircraft Propulsion 2

Component Analysis • Diffuser – Free Stream to Diffuser Inlet – Diffuser Inlet to Outlet • Nozzle – Fixed Divergent Nozzle – Diverging Converging Nozzle • Axial Flow Compressor • Axial Flow Turbine November 17, 2012 Aircraft Propulsion 3

Engine without Inlet Cone • Free Stream to Diffuser Inlet • Subsonic Flow • Supersonic Flow with Shock • Diffuser Inlet to Outlet • Ideal Diffuser – Isentropic Flow • Non Ideal Diffuser – Fanno Line Flow November 17, 2012 Aircraft Propulsion 4

Free Stream to Diffuser Inlet πo represents loss from free stream to the inlet. Supersonic Flow Shock • πo < 1 Subsonic Flow • πo ≈ 1 (= 1: ideal isentropic flow) November 17, 2012 Aircraft Propulsion 5

Supersonic Flow with Normal Shocks • Shocks usually occur exterior to, or near, the inlet plane of the diffuser when an aircraft flies supersonically. • The strongest shocks is the normal shocks. Oct. 13, 2012 Aircraft Propulsion 6

Ex 1: Normal Shocks A standing normal shock occurs on an aircraft flying at Mach 1. 50. The internal recovery factor of the diffuser is 0. 98, and the specific heat ratio is 1. 40. Find the total recovery factor of the diffuser. Oct. 13, 2012 Aircraft Propulsion 7

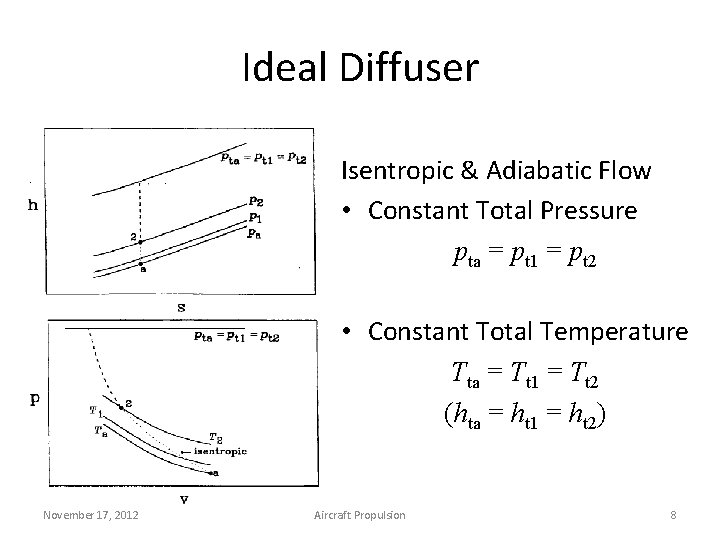
Ideal Diffuser Isentropic & Adiabatic Flow • Constant Total Pressure pta = pt 1 = pt 2 • Constant Total Temperature Tta = Tt 1 = Tt 2 (hta = ht 1 = ht 2) November 17, 2012 Aircraft Propulsion 8

Isentropic Flow Mach Number and Local Speed of Sound Stagnation Relations Area Ratio Oct. 13, 2012 Aircraft Propulsion 9

Limit on Pressure Rise Separation is one of the limits of the diffuser operation. Aligned Inlet Flow: for flow without separation. Mis-Aligned Inlet Flow: Upper limit on the pressure coefficient will be reduced appreciably to perhaps 0. 1 to 0. 2. Oct. 13, 2012 Aircraft Propulsion 10

Ex 2: Separation Limit Design an ideal diffuser to attain the maximum pressure rise if the incoming Mach no. is 0. 8. That is find the diffuser area ratio, pressure ratio and the resulting exit Mach number. Assuming isentropic flow and γ = 1. 4. Oct. 13, 2012 Aircraft Propulsion 11

Non Ideal Diffuser Low Speed/Flow To quantify loss from the free accelerates/Pressure stream to the diffuser exit, we decreases introduce: High Speed/Flow decelerates/ • Total Pressure Recovery Factor: Pressure increases where • πr is the diffuser pressure recovery factor, and • πo represents loss from free stream to the inlet. November 17, 2012 Nearly Adiabatic Flow, assume: • Constant Total Enthalpy hta = ht 1 = ht 2 • Constant Total Temperature Tta = Tt 1 = Tt 2 Aircraft Propulsion 12

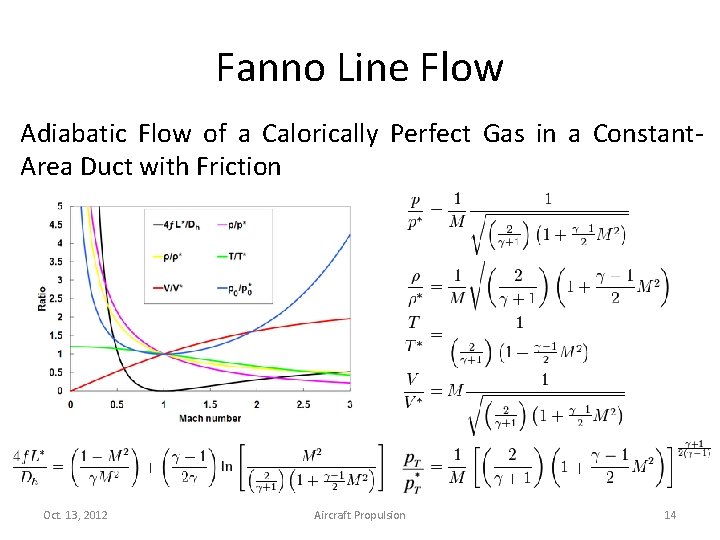
Friction Flow Viscous flows are the primary means by which total pressure losses occur!! Fanno Line Flow: flow with friction but no heat transfer Fanno Line Flow could be used when: • Exit-to-inlet area ratio is near unity, • The flow does not separate. Oct. 13, 2012 Aircraft Propulsion 13

Fanno Line Flow Adiabatic Flow of a Calorically Perfect Gas in a Constant. Area Duct with Friction Oct. 13, 2012 Aircraft Propulsion 14

Engine with Inlet Cone • Oblique Shock – Oblique Planar Shock – Oblique Conical Shock • Mode of Operation – Design Condition – Off Design Condition November 17, 2012 Aircraft Propulsion 15

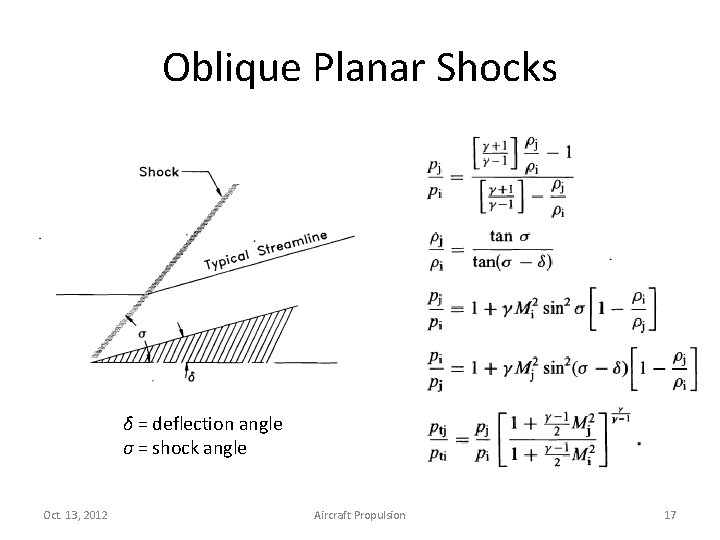
Oblique Planar Shocks • 2 D planar shock is simpler than conical shock. • Occur when an inlet is attached to the fuselage of the aircraft, the inlet is more or less rectangular, resulting in planar shock. • Flow behind the planar shock is uniformly parallel to the wedge. Oct. 13, 2012 Aircraft Propulsion 16

Oblique Planar Shocks δ = deflection angle σ = shock angle Oct. 13, 2012 Aircraft Propulsion 17

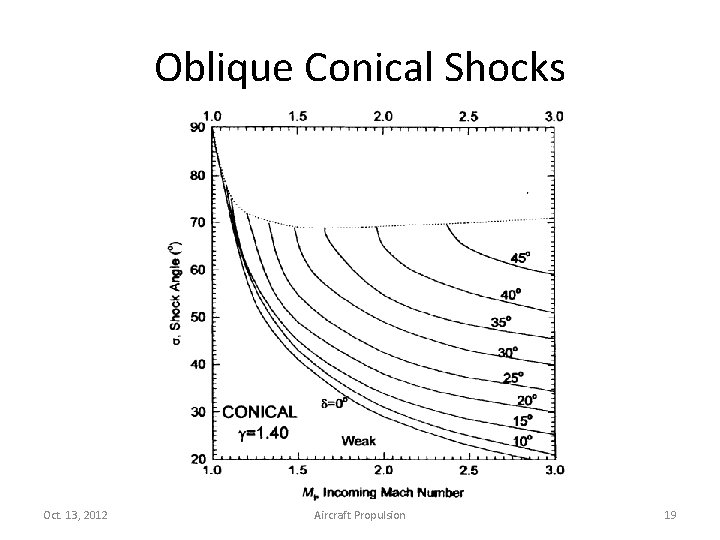
Oblique Conical Shocks • Found in many aircraft applications. • A conical ramp is used to generate an oblique shock, which decelerate flow to a less supersonic conditions. • A normal shock further decelerates the flow to a subsonic condition for the internal flow in the diffuser. Spike on Black. Bird Oct. 13, 2012 Aircraft Propulsion 18

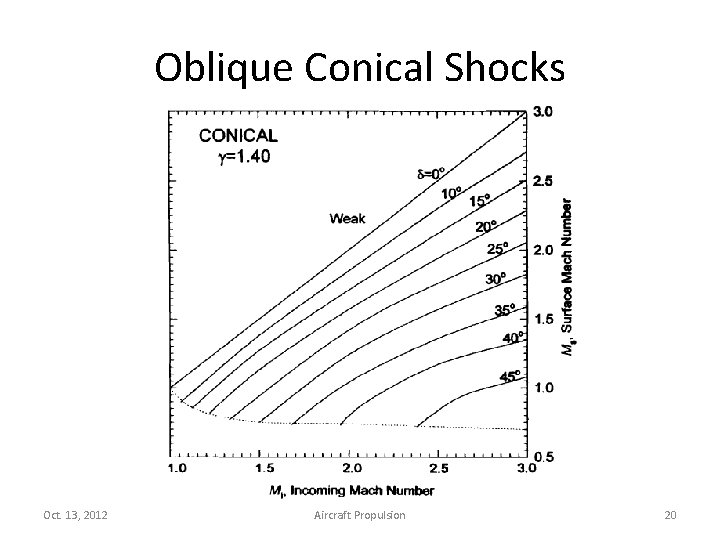
Oblique Conical Shocks Oct. 13, 2012 Aircraft Propulsion 19

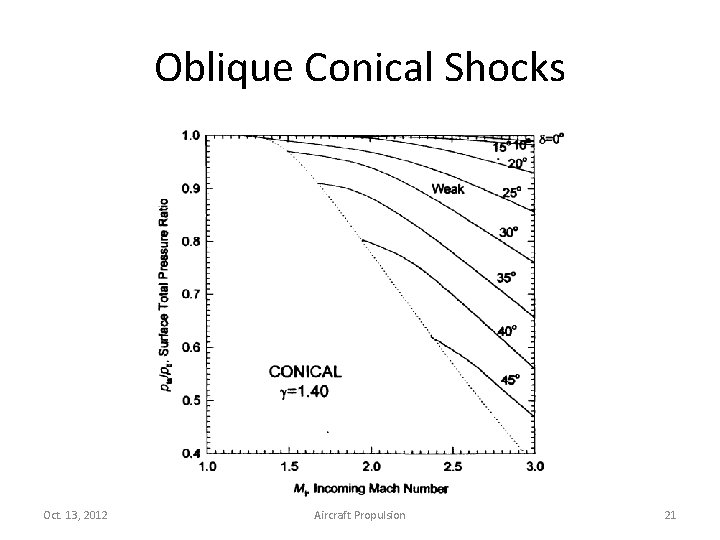
Oblique Conical Shocks Oct. 13, 2012 Aircraft Propulsion 20

Oblique Conical Shocks Oct. 13, 2012 Aircraft Propulsion 21

Modes of Operation Design Condition: the oblique shock intersects the diffuser cowl All the air that cross oblique shock enters the engine Flow rate decreases Pressure in the diffuser decreases Mach no. in the diffuser decreases Shock is pushed out!! Shock is stronger larger total pressure loss Some of the air will be spilled high pressure additive drag Shock is used to compress air outside shock wasting power Flow rate increases Pressure in the diffuser drops Shock moves into the diffuser Acting like a supersonic nozzle Shock occurs in diverging section with high Mach no. More total pressure is lost. Oct. 13, 2012 Aircraft Propulsion 22

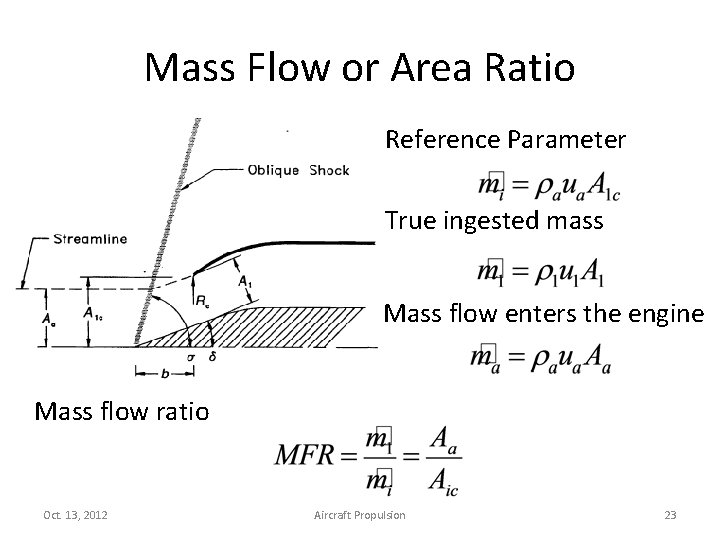
Mass Flow or Area Ratio Reference Parameter True ingested mass Mass flow enters the engine Mass flow ratio Oct. 13, 2012 Aircraft Propulsion 23

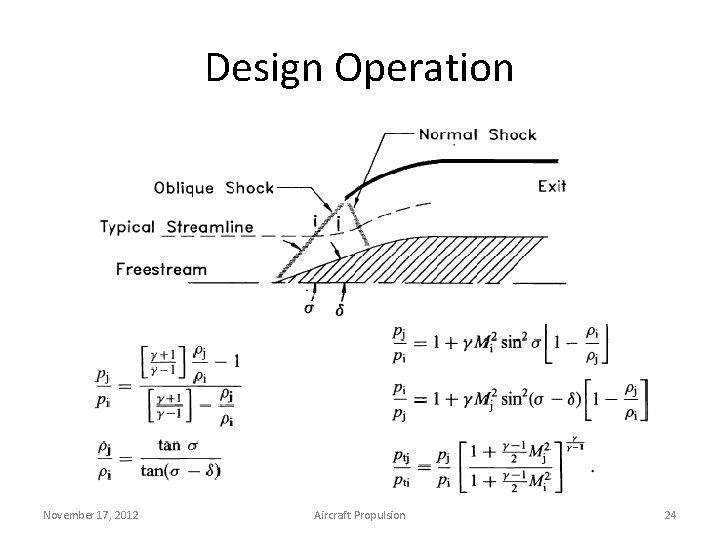
Design Operation November 17, 2012 Aircraft Propulsion 24

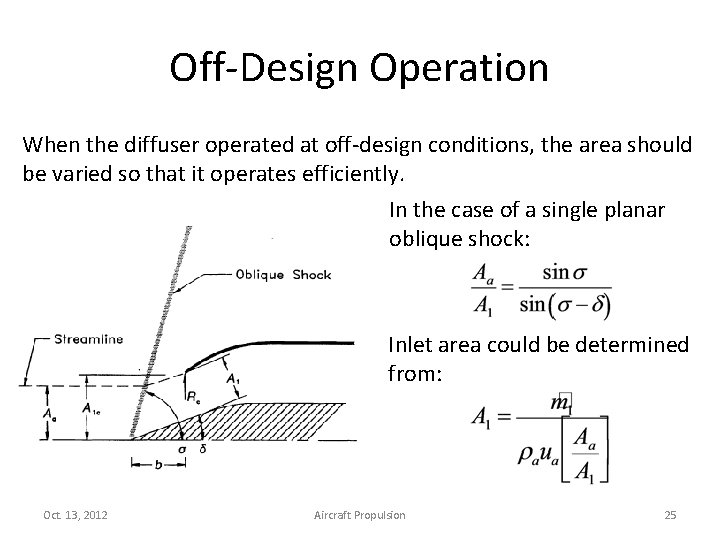
Off-Design Operation When the diffuser operated at off-design conditions, the area should be varied so that it operates efficiently. In the case of a single planar oblique shock: Inlet area could be determined from: Oct. 13, 2012 Aircraft Propulsion 25

Ex 3: Supersonic Diffuser A diffuser with a spike is used on a supersonic aircraft. The freestream Mach number is 2. 2, and the cone halfangle is 24°. The standing oblique shock is attached to the spike and cowl, and a converging inlet section with a throat of area Am is used to decelerate the flow through internal compression. Assume γ = 1. 4 and πr = 0. 98. a. Estimate πd on the assumption the inlet starts. Also, find the required Am/A 1 b. Find πd on the assumption the inlet doesn’t start and has a standing normal shock located in front of the spike. Oct. 13, 2012 Aircraft Propulsion 26

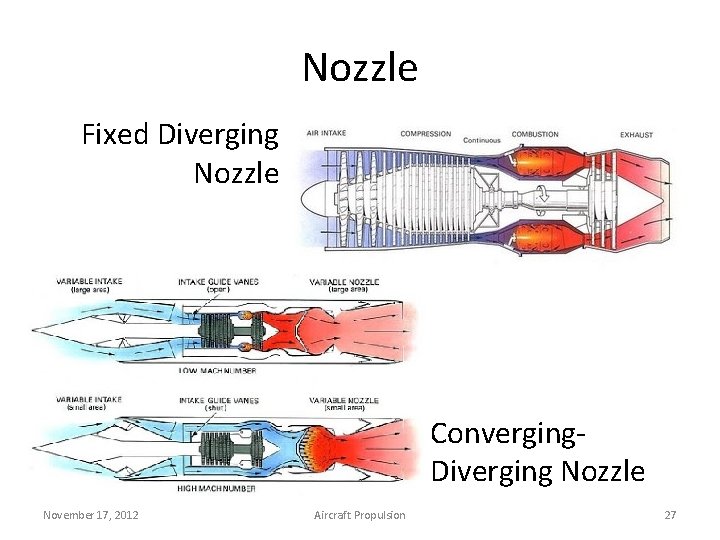
Nozzle Fixed Diverging Nozzle Converging. Diverging Nozzle November 17, 2012 Aircraft Propulsion 27

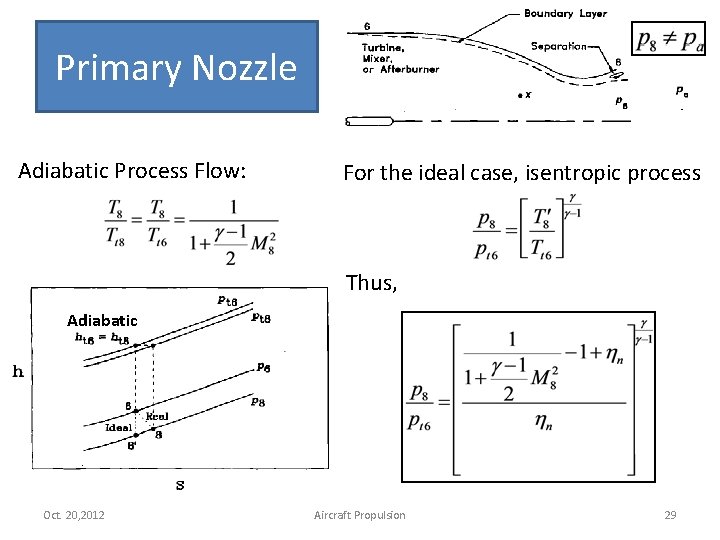
Primary Nozzle In real analysis: Ø Pexit may not match Pa due to incorrect nozzle area proportion. Ø Frictional losses are include but adiabatic process still be assumed. Nozzle Efficiency Constant cp Specific heat Adiabatic Exit Velocity Oct. 20, 2012 Aircraft Propulsion 28

Primary Nozzle Adiabatic Process Flow: For the ideal case, isentropic process Thus, Adiabatic Oct. 20, 2012 Aircraft Propulsion 29

Primary Nozzle Choke condition: If p* > pa, the nozzle is choke If p*= p 8, M 8 = 1 If p* < pa , M 8 < 1 and p 8 = pa Then, Oct. 20, 2012 Aircraft Propulsion 30

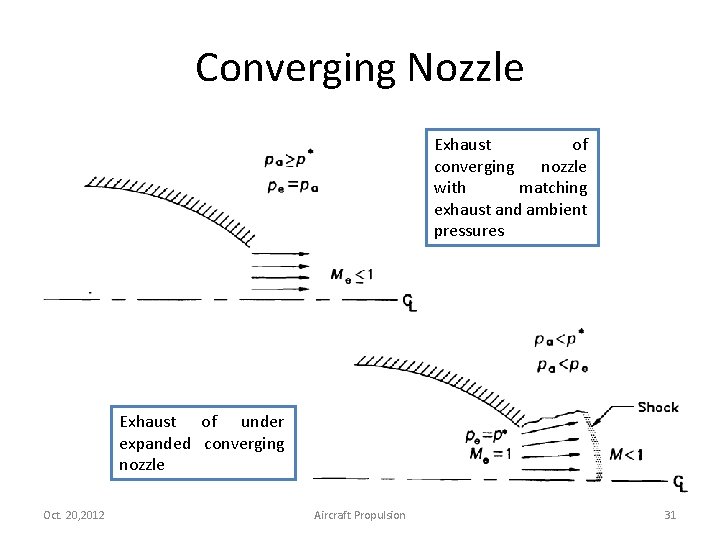
Converging Nozzle Exhaust of converging nozzle with matching exhaust and ambient pressures Exhaust of under expanded converging nozzle Oct. 20, 2012 Aircraft Propulsion 31

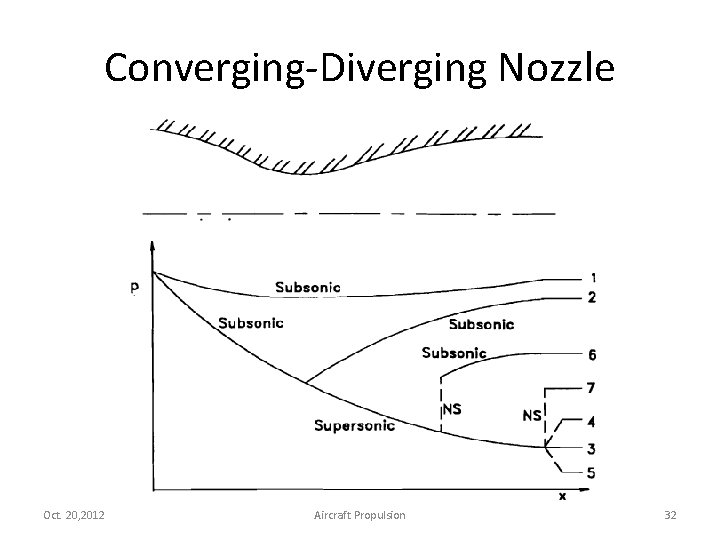
Converging-Diverging Nozzle Oct. 20, 2012 Aircraft Propulsion 32

1 st – 3 rd Condition of CD nozzle • Case 1: pexhaust = pambient and Subsonic Flow Through out the nozzle. • Case 2: pexhaust = pambient and Subsonic Flow Through out the nozzle but Mthroat =1. • Case 3: pexhaust = pambient , Subsonic Flow in the converging section and Supersonic Flow in the diverging section. – MAXIMUM THRUST – Design Condition for the ideal case Oct. 20, 2012 Aircraft Propulsion 33

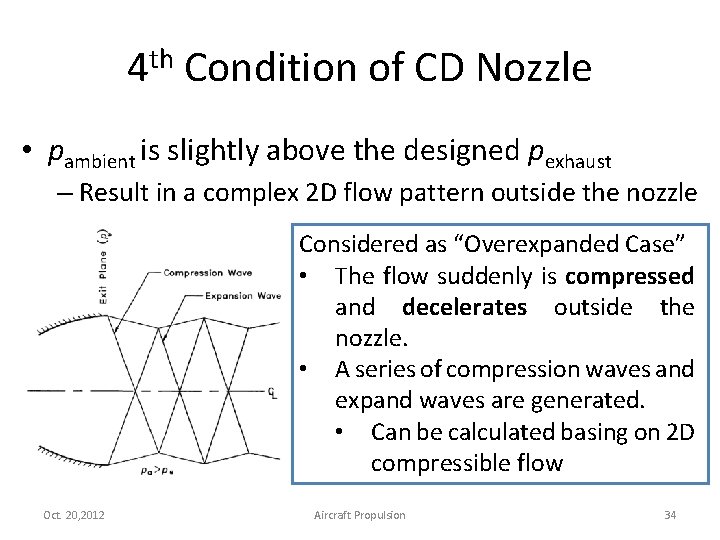
4 th Condition of CD Nozzle • pambient is slightly above the designed pexhaust – Result in a complex 2 D flow pattern outside the nozzle Considered as “Overexpanded Case” • The flow suddenly is compressed and decelerates outside the nozzle. • A series of compression waves and expand waves are generated. • Can be calculated basing on 2 D compressible flow Oct. 20, 2012 Aircraft Propulsion 34

5 th Condition of CD Nozzle • pambient is below the designed pexhaust – Result in a complex 2 D flow pattern outside the nozzle Considered as “Underexpanded Case” or “Super Critical Case” • The flow continues to expand accelerates outside the nozzle. • A series of compression waves and expanded waves are generated resulting in a series of shock diamonds. Oct. 20, 2012 Aircraft Propulsion 35

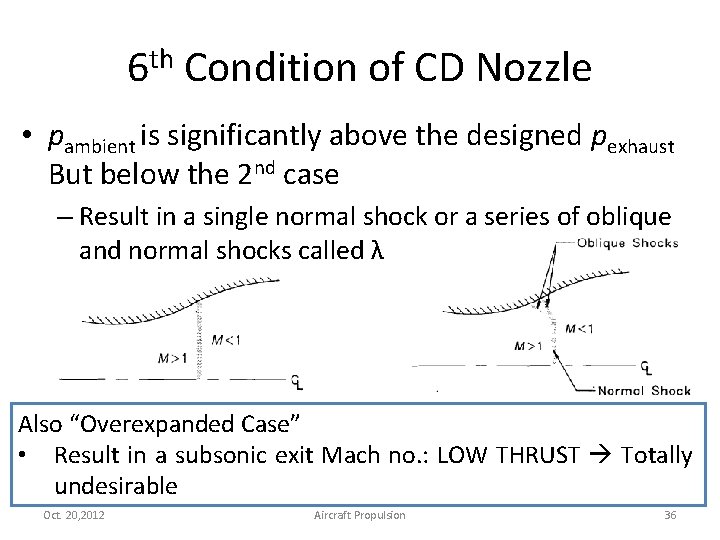
6 th Condition of CD Nozzle • pambient is significantly above the designed pexhaust But below the 2 nd case – Result in a single normal shock or a series of oblique and normal shocks called λ Also “Overexpanded Case” • Result in a subsonic exit Mach no. : LOW THRUST Totally undesirable Oct. 20, 2012 Aircraft Propulsion 36

7 th Condition of CD Nozzle • pambient is significantly above the designed pexhaust Limit condition of the 6 th case – Exit pressure causes a normal shock exactly at the exit plane – Case 4 falls between case 7 and 3. Oct. 20, 2012 Aircraft Propulsion 37

Ex 4: Converging-Diverging Nozzle A converging-diverging nozzle with an exit area of 0. 2258 m 2 and a minimum area of 0. 1774 m 2 has an upstream total pressure of 137. 895 k. Pa. The nozzle efficiency is 0. 965 and the specific heat ratio is 1. 35. a. At what atmospheric pressure will the nozzle flow be shockless? b. At what atmospheric pressure will a normal shock stand in the exit plane? Oct. 20, 2012 Aircraft Propulsion 38

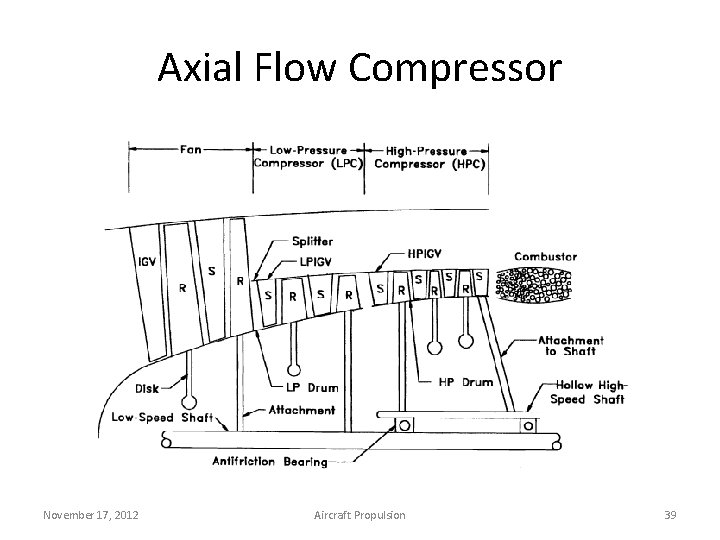
Axial Flow Compressor November 17, 2012 Aircraft Propulsion 39

Velocity Polygon November 17, 2012 Aircraft Propulsion 40

Total Pressure Ratio The equations is derived for a single stage (rotor and stator) using 2 D planar mean line c. v. approach. “Midway between hub and tip” • Power Input to the Shaft • Total Pressure Ratio of the Stage Control Volume definition for compressor stage October 27, 2012 Aircraft Propulsion 41

Percent Reaction A relation that approximates the relative loading of the rotor and stator based on the enthalpy rise: October 27, 2012 Aircraft Propulsion 42

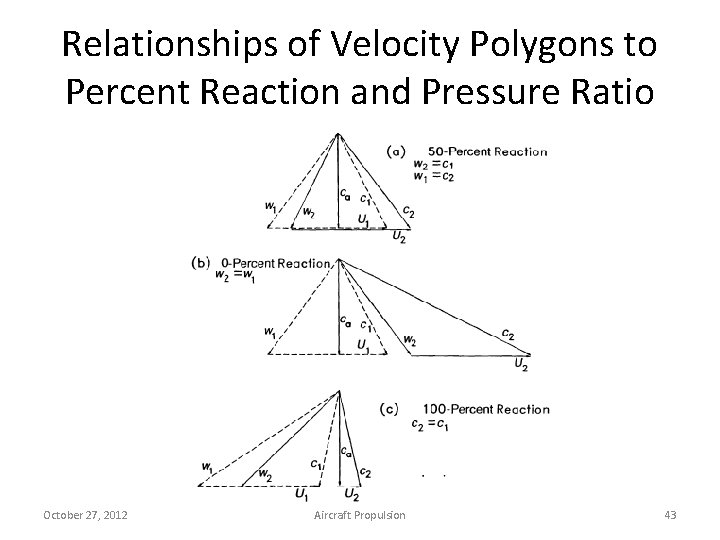
Relationships of Velocity Polygons to Percent Reaction and Pressure Ratio October 27, 2012 Aircraft Propulsion 43

Limit on Stage Pressure Ratio • The rotor is moving, the relative velocity must be used: • For the stator, which is stationary the relative velocity must be used: 1 and 2 refer to the stage inlet and midstage properties. October 27, 2012 Aircraft Propulsion 44

Limit on Stage Pressure Ratio Rotor October 27, 2012 Stator Aircraft Propulsion 45

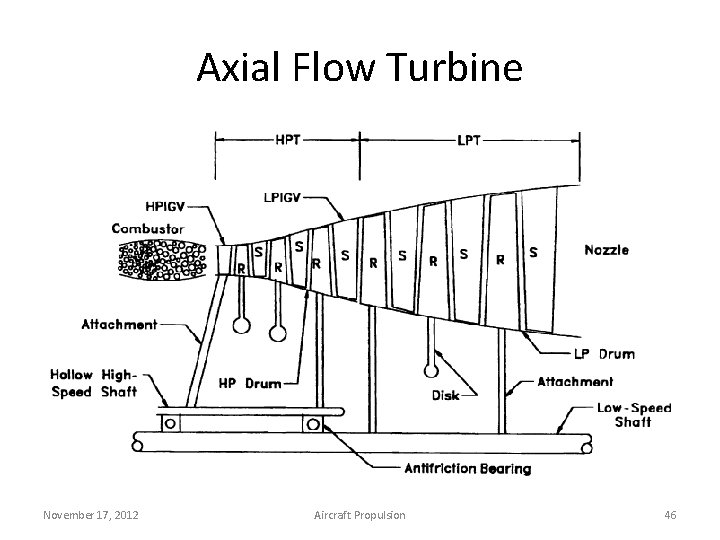
Axial Flow Turbine November 17, 2012 Aircraft Propulsion 46

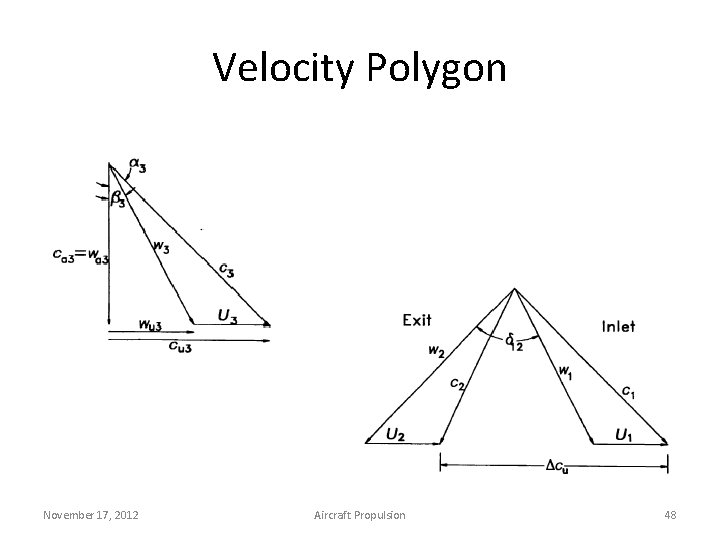
Velocity Polygon November 17, 2012 Aircraft Propulsion 47

Velocity Polygon November 17, 2012 Aircraft Propulsion 48

Total Pressure Ratio The equations is derived for a single stage (rotor and stator) using 2 D planar mean line c. v. approach. “Midway between hub and tip” The continuity, momentum and energy equations are used for the delivered shaft power: • Power Input to the Shaft • Total Pressure Ratio of the Stage November 17, 2012 Aircraft Propulsion 49

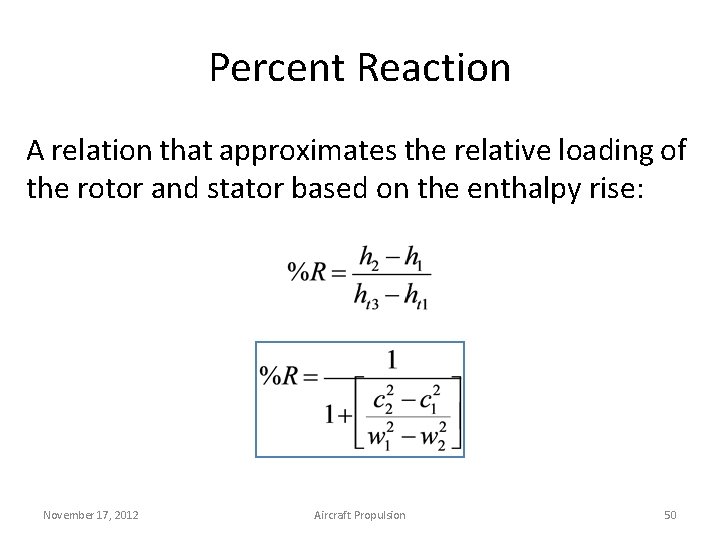
Percent Reaction A relation that approximates the relative loading of the rotor and stator based on the enthalpy rise: November 17, 2012 Aircraft Propulsion 50

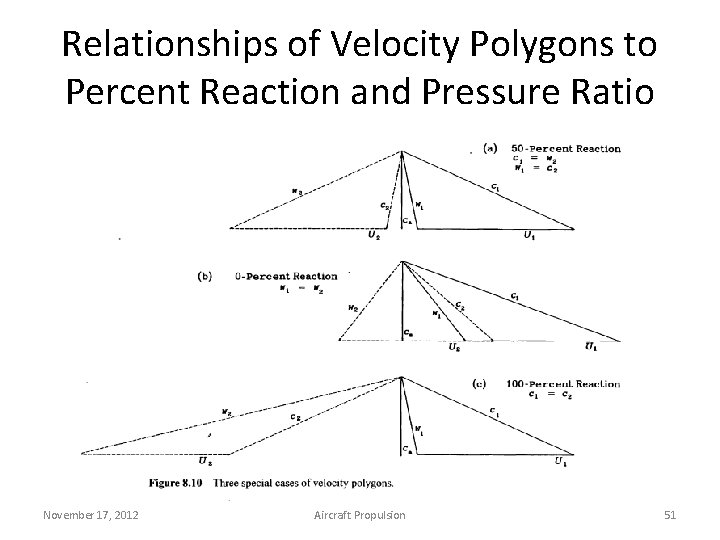
Relationships of Velocity Polygons to Percent Reaction and Pressure Ratio November 17, 2012 Aircraft Propulsion 51

Turbine and Compressor Matching 1. 2. 3. 4. 5. Select operating speed. Assume turbine inlet temperature. Assume compressor pressure ratio. Calculate compressor work. Calculate turbine pressure ratio required to produce this work. November 17, 2012 Aircraft Propulsion 52

Turbine and Compressor Matching 6. Check to see if compressor mass flow plus fuel flow equals turbine mass flow; if it does not, assume a new value of compressor pressure ratio and repeat step 4, 5, and 6 until continuity is satisfied. Note: No need to do the iteration in the exam, I will provide a required values to determine other value. November 17, 2012 Aircraft Propulsion 53

Turbine and Compressor Matching Note: No need to do the iteration in the exam, I will provide a required values to determine the others from compressor and turbine performance maps. Ex. For given rotational speed, mass flow rate and total pressure ratio across each component, efficiency could be determined. November 17, 2012 Aircraft Propulsion 54

Good Luck!!! November 17, 2012 Aircraft Propulsion 55