Review of Complex numbers Rectangular Form Imag Exponential

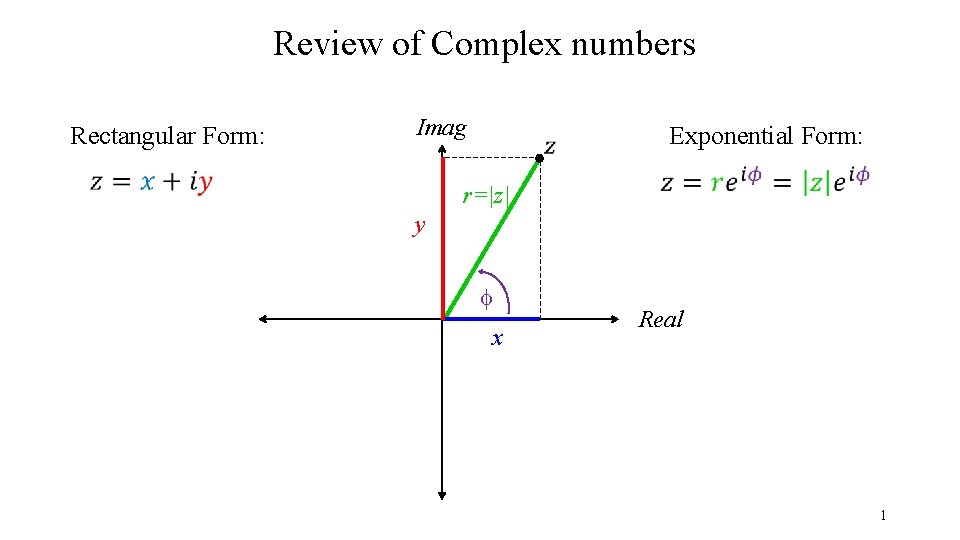
Review of Complex numbers Rectangular Form: Imag Exponential Form: r=|z| y f x Real 1

Real & Imaginary Parts of Rectangular Form The real and imaginary parts of a complex number in rectangular form are real numbers: Imag y=Im(z) Therefore, rectangular form can be equivalently written as: x=Re(z) Real

Geometry Relating the Forms The real and imaginary components of exponential form can be found using trigonometry: Imag r=|z| f x Real Imag r=|z| y f Real

Geometry Relating the Forms: Real & Imaginary Parts The real and imaginary parts of a complex number can be expressed as follows: Imag r=|z| Real

Geometry Relating the Forms: Quadrants Imag r=|z| y Real f x Real

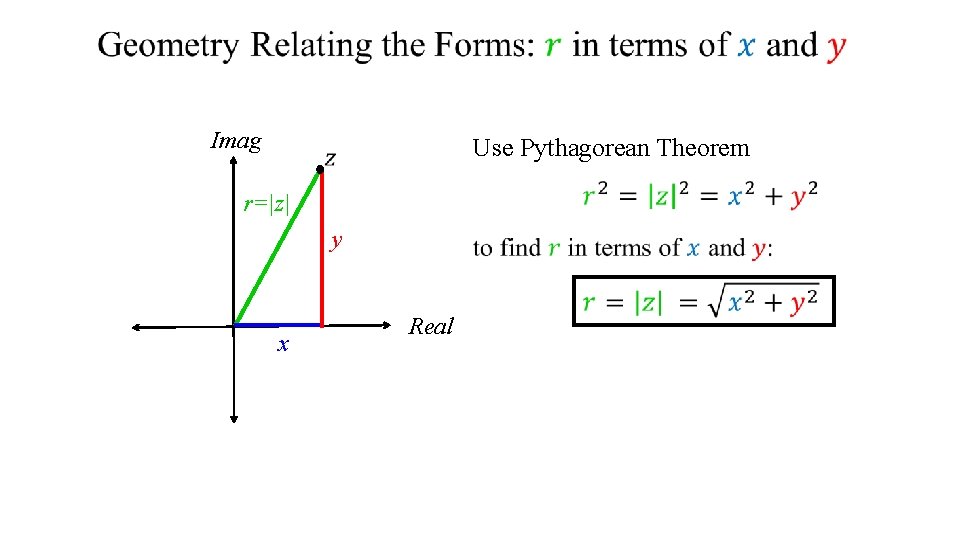
Imag Use Pythagorean Theorem r=|z| y x Real

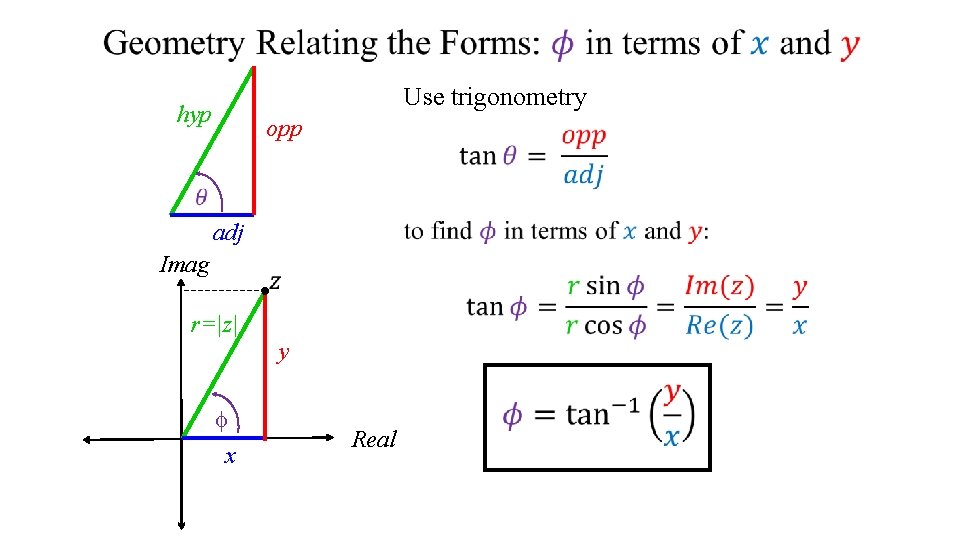
Use trigonometry hyp opp adj Imag r=|z| y f x Real

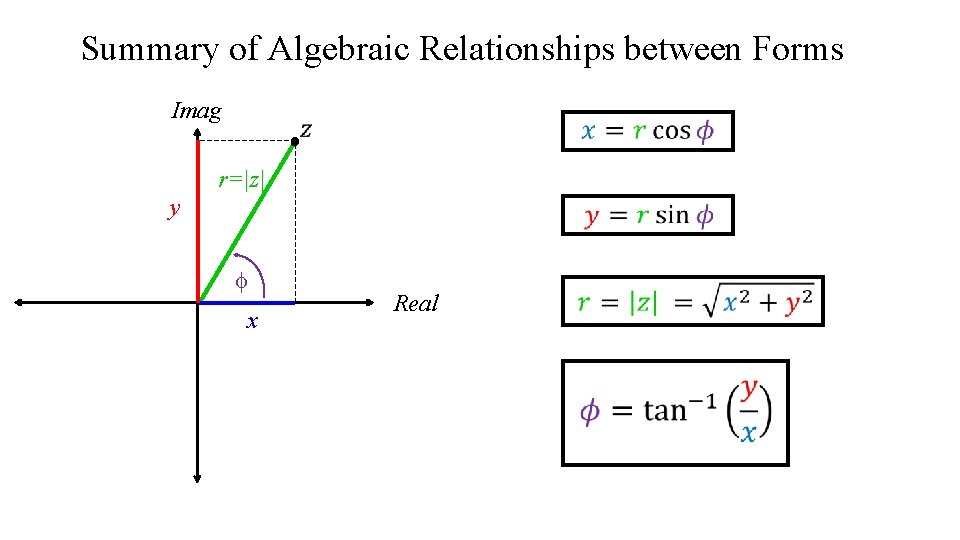
Summary of Algebraic Relationships between Forms Imag r=|z| y f x Real

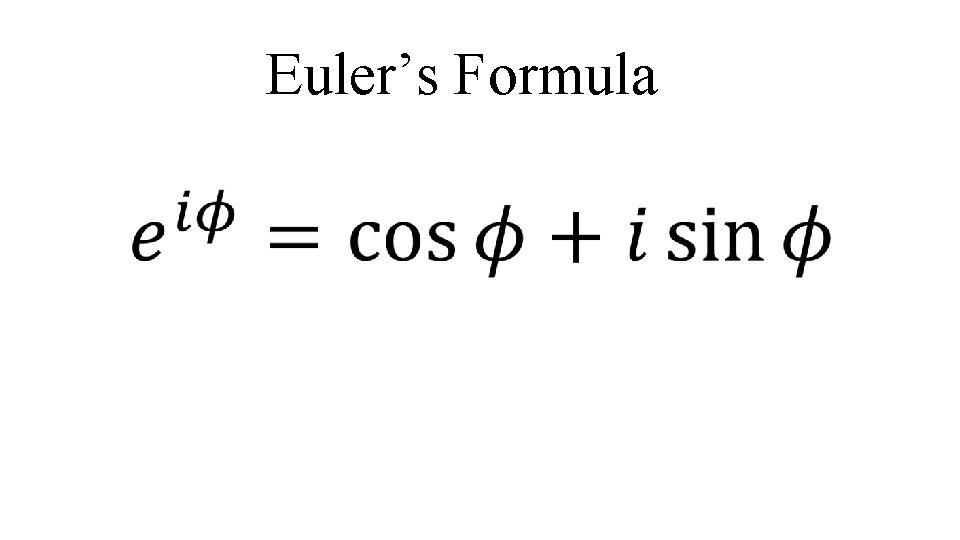
Euler’s Formula

Consistency argument If these represent the same thing, then the assumed Euler relationship says: Rectangular Form: Exponential Form:

Euler’s Formula Can be used with functions: 11

Addition & Subtraction of Complex Numbers Addition and subtraction of complex numbers is easy in rectangular form Addition and subtraction are analogous to vector addition and subtraction y Imag b b a c d Real a c x d 12

Multiplication of Complex Numbers Multiplication of complex numbers is easy in exponential form Imag Real 13

Division of Complex Numbers Division of complex numbers is easy in exponential form Division of complex numbers is sometimes easy in rectangular form Multiply by 1 using the complex conjugate of the denominator 14

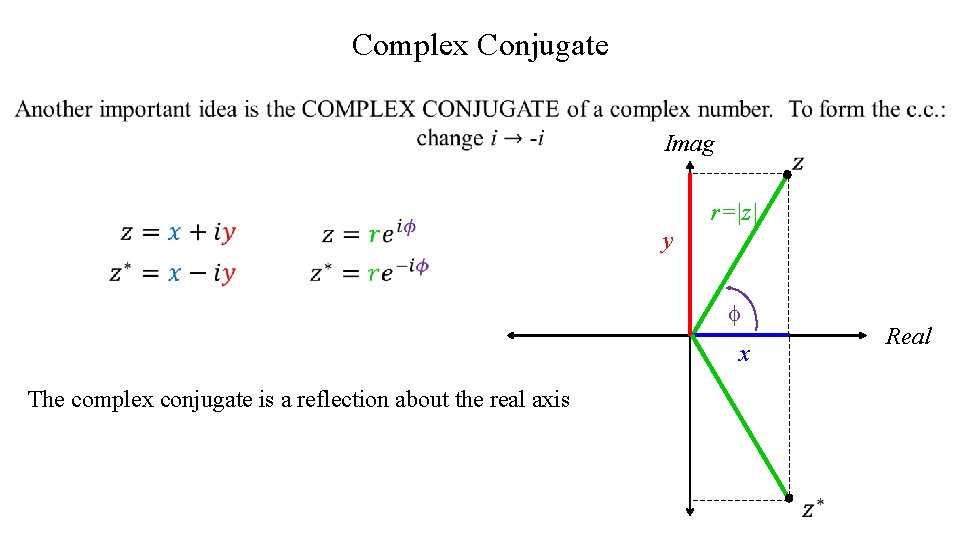
Complex Conjugate Imag r=|z| y f x The complex conjugate is a reflection about the real axis Real

Common Operations with the Complex Conjugate Addition of the complex number and its complex conjugate results in a real number Imag r=|z| y The product of a complex number and its complex conjugate is REAL. f x Real