Review of Basics and Elementary introduction to quantum

Review of Basics and Elementary introduction to quantum postulates

Requirements On Mathematics Apparatus • Physical states • Mathematic entities • Interference phenomena • Nondeterministic predictions • Model the effects of measurement • Distinction between evolution and measurement

What’s Quantum Mechanics • A mathematical framework • Description of the world known • Rather simple rules but counterintuitive applications

Introduction to Linear Algebra • Quantum mechanics ØThe basis for quantum computing and quantum information • Why Linear Algebra? ØPrerequisities • What is Linear Algebra concerning? ØVector spaces ØLinear operations

Basic linear algebra useful in QM • • Complex numbers Vector space Linear operators Inner products Unitary operators Tensor products …

Dirac-notation: Bra and Ket • For the sake of simplification • “ket” stands for a vector in Hilbert • “bra” stands for the adjoint of • Named after the word “bracket”

Hilbert Space Fundamentals • Inner product space: linear space equipped with inner product • Hilbert Space (finite dimensional): can be considered as inner product space of a quantum system • Orthogonality: • Norm: • Unit vector parallel to |v :

Hilbert Space (Cont’d) • Orthonormal basis: a basis set where • Can be found from an arbitrary basis set by Gram-Schmidt Orthogonalization

Inner Products

Inner Products • Inner Product is a function combining two vectors • It yields a complex number • It obeys the following rules • •

Unitary Operator • An operator U is unitary, if • Preserves Inner product

Tensor Product • Larger vector space formed from two smaller ones • Combining elements from each in all possible ways • Preserves both linearity and scalar multiplication

Qubit on Bloch Sphere

Mathematically, what is a qubit ? (1) • We can form linear combinations of states • A qubit state is a unit vector in a two dimensional complex vector space

Qubits Cont'd • We may rewrite as… We can ignore eia as it has no observable effect • From a single measurement one obtains only a single bit of information about the state of the qubit • There is "hidden" quantum information and this information grows exponentially

Any pair of linearly independent vectors can be a basis!

Measurements of the same qubit in various bases 1/ 2

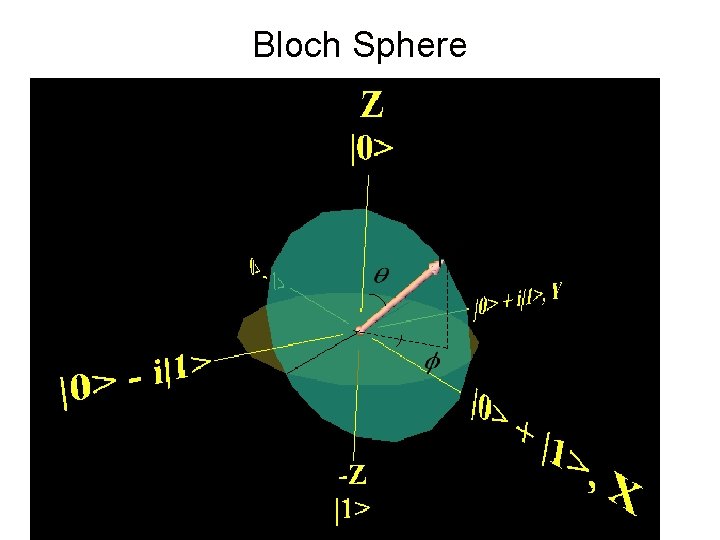
Bloch Sphere

Measurements

AXIOMS OF QUANTUM MECHANICS

Postulates in QM • Why are postulates important? Ø… they provide the connections between the physical, real, world and the quantum mechanics mathematics used to model these systems - Isaak L. Chuang 24

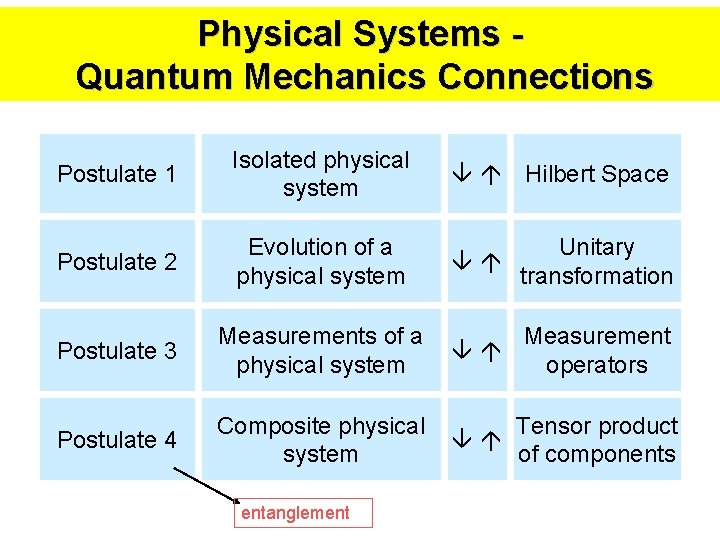
Physical Systems Quantum Mechanics Connections Postulate 1 Isolated physical system Hilbert Space Postulate 2 Evolution of a physical system Unitary transformation Postulate 3 Measurements of a physical system Postulate 4 Composite physical system Tensor product of components entanglement Measurement operators

Summary on Postulates

Postulate 3 in rough form

From last slide

compare Manin was first

Postulate 4 You can apply the constant to each Distributive properties

Entanglement

Entanglement

Some convenctions implicit in postulate 4

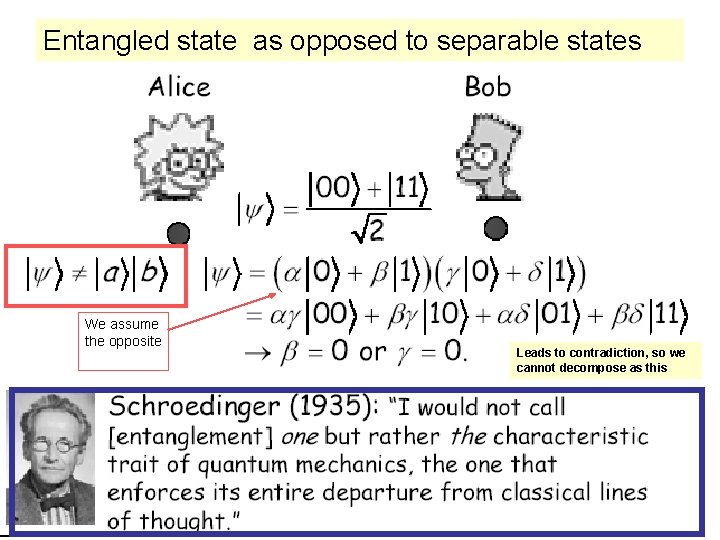
Entangled state as opposed to separable states We assume the opposite Leads to contradiction, so we cannot decompose as this

Composed quantum systems – results of Postulate 4

Composite quantum system

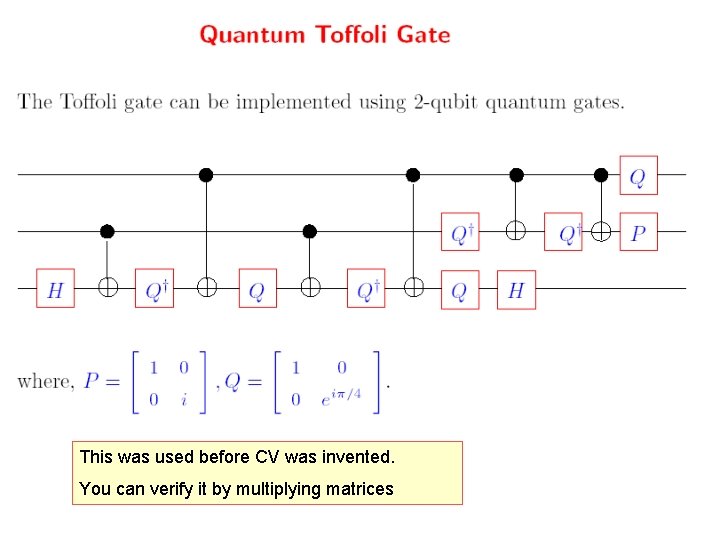
This was used before CV was invented. You can verify it by multiplying matrices

The Measurement Problem Can we deduce postulate 3 from 1 and 2? Joke. Do not try it. Slides are from MIT.

Sources Quantum Computing Mathematics and Postulates Anuj Dawar , Michael Nielsen Presented by Chensheng Qiu Supervised by Dplm. Ing. Gherman Advanced topic seminar SS 02 “Innovative Computer architecture and concepts” Examiner: Prof. Wunderlich

• Covered in 2007, 2011