Review of Basic Statistical Concepts Farideh DehkordiVakil Review

Review of Basic Statistical Concepts Farideh Dehkordi-Vakil

Review of Basic Statistical Concepts n Descriptive Statistics n Methods that organize and summarize data. n n n Numerical summary Graphical Methods Inferential Statistics n Generalizing from a sample to the population from which it was selected. n n Estimation Hypothesis testing

Review of Basic Statistical Concepts n Population n n The entire collection of individuals or objects about which information is desired. Sample n A subset of the population selected in some prescribed manner for study.

Review of Basic Statistical Concepts n Numerical summaries n Measure of central tendencies n n n Mean Median Measure of variability n n n Variance, Standard deviation Range Quartiles

Review of Basic Statistical Concepts n The Mean n n To find the mean of a set of observations, add their values and divide by the number of observations. If the n observations are , their mean is In a more compact notation,

Example: Books Page Length A sample of n = 8 books is selected from a library’s collection, and page length of each one is determined, resulting in the following data set. X 1=247, X 2=312, X 3=198, X 4=780, X 5=175, X 6=286, X 7=293, X 8=258

Review of Basic Statistical Concepts n Median M n The Median M is the midpoint of a distribution, the number such that half of the observations are smaller and the other half are larger. To find the median of a distribution: 1. 2. 3. Arrange all observations in order of size, from smallest to largest. If the number of observations n is odd, the median M is the center observation in the ordered list. If the number of observations n is even, the median M is the mean of the two center observations in the ordered list.

Review of Basic Statistical Concepts n Quartiles Q 1 and Q 3 n To calculate the quartiles: 1. 2. 3. Arrange the observations in increasing order and locate the median M in the ordered list of observations. The first quartile Q 1 is the median of the observations whose position in the ordered list is to the left of the location of the overall median. The third quartile Q 3 is the median of the observations whose position in the ordered list is to the right of the location of the overall median.

Example: Books Page Length n Median: n Order the list 175, 198, 247, 258, 286, 293, 312, 780 n n There are two middle numbers 258, and 286. The median is the average of these two numbers

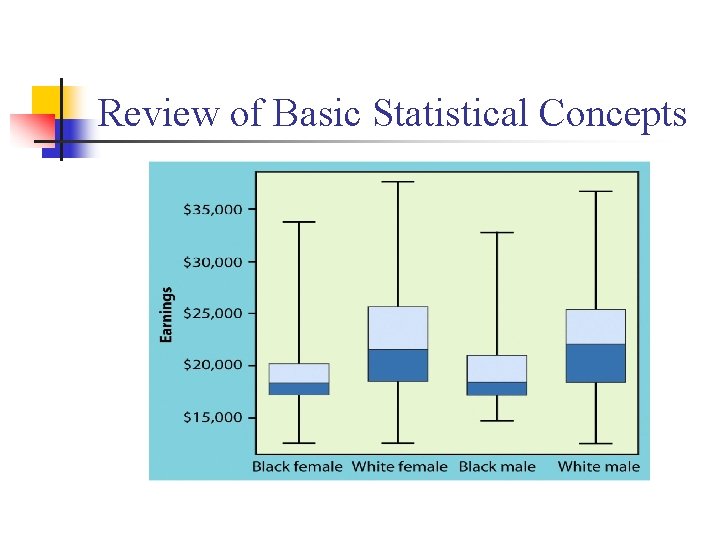
Review of Basic Statistical Concepts n The Five Number Summary and Box-Plot n The five number summary of a distribution consists of the smallest observation, the first quartile, the median, the third quartile, and the largest observation, written in order from smallest to largest. In symbols, the five number summary is: Minimum Q 1 M Q 3 Maximum

Review of Basic Statistical Concepts n A box-plot is a graph of the five number Summary. n n A central box spans the quartiles. A line in the box marks the median. Lines extend from the box out to the smallest and largest observations. Box-plots are most useful for side-by-side comparison of several distributions.
Review of Basic Statistical Concepts

Review of Basic Statistical Concepts n The Variance s 2 n n The Variance s 2 of a set of observations is the average of the squares of the deviations of the observations from their mean. In symbols, the variance of n observations is or, more compactly,

Review of Basic Statistical Concepts n The Standard Deviation s n n The standard deviation s is the square root of the variance s 2: Computational formula for variance

Example: Book page length

Review of Basic Statistical Concepts n Choosing a Summary n The five number summary is usually better than the mean and standard deviation for describing a skewed distribution or a distribution with extreme outliers. Use , and s only for reasonably symmetric distributions that are free of outliers.

Review of Basic Statistical Concepts n Introduction to Inference n n n The purpose of inference is to draw conclusions from data. Conclusions take into account the natural variability in the data, therefore formal inference relies on probability to describe chance variation. We will go over the two most prominent types of formal statistical inference n n n Confidence Intervals for estimating the value of a population parameter. Tests of significance which asses the evidence for a claim. Both types of inference are based on the sampling distribution of statistics.

Review of Basic Statistical Concepts n Parameters and Statistics n A parameter is a number that describes the population. n n A parameter is a fixed number, but in practice we do not know its value. A statistic is a number that describes a sample. n n The value of a statistic is known when we have taken a sample, but it can change from sample to sample. We often use statistic to estimate an unknown parameter.

Review of Basic Statistical Concepts n n n Since both methods of formal inference are based on sampling distributions, they require probability model for the data. The model is most secure and inference is most reliable when the data are produced by a properly randomized design. When we use statistical inference we assume that the data come from a randomly selected sample (SRS) or a randomized experiment.

Example: Consumer attitude towards shopping n A recent survey asked a nationwide random sample of 2500 adults if they agreed or disagreed with the following statement I like buying new cloths, but shopping is often frustrating and time consuming. n n Of the respondents, 1650 said they agreed. The proportion of the sample who agreed that cloths shopping is often frustrating is:

Example: Consumer attitude towards shopping n n n The number =. 66 is a statistic. The corresponding parameter is the proportion (call it P) of all adult U. S. residents who would have said “Yes” if asked the same question. We don’t know the value of parameter P, so we use as its estimate.

Review of Basic Statistical Concepts n n If the marketing firm took a second random sample of 2500 adults, the new sample would have different people in it. It is almost certain that there would not be exactly 1650 positive responses. That is, the value of will vary from sample to sample. Random samples eliminate bias from the act of choosing a sample, but they can still be wrong because of the variability that results when we choose at random.

Review of Basic Statistical Concepts n n n The first advantage of choosing at random is that it eliminates bias. The second advantage is that if we take lots of random samples of the same size from the same population, the variation from sample to sample will follow a predictable pattern. All statistical inference is based on one idea: to see how trustworthy a procedure is, ask what would happen if we repeated it many times.

Review of Basic Statistical Concepts n Sampling Distribution of Statistics n n Suppose that exactly 60% of adults find shopping for cloths frustrating and time consuming. That is, the truth about the population is that P = 0. 6. (parameter) We select a SRS (Simple Random Sample) of size 100 from this population and use the sample proportion( , statistic) to estimate the unknown value of the population proportion P. What is the distribution of ?

Review of Basic Statistical Concepts n To answer this question: n n Take a large number of samples of size 100 from this population. Calculate the sample proportion for each sample. Make a histogram of the values of. Examine the distribution displayed in the histogram for shape, center, and spread, as well as outliers or other deviations.
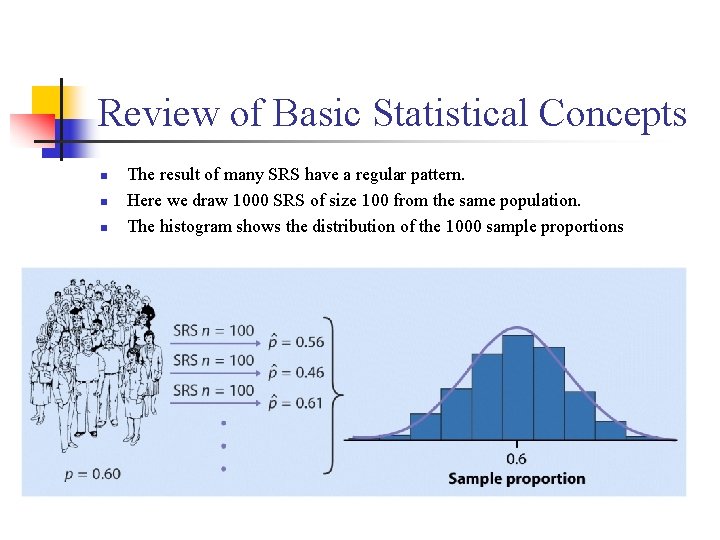
Review of Basic Statistical Concepts n n n The result of many SRS have a regular pattern. Here we draw 1000 SRS of size 100 from the same population. The histogram shows the distribution of the 1000 sample proportions

Review of Basic Statistical Concepts n Sampling Distribution n The sampling distribution of a statistic is the distribution of values taken by the statistic in all possible samples of the same size from the same population.
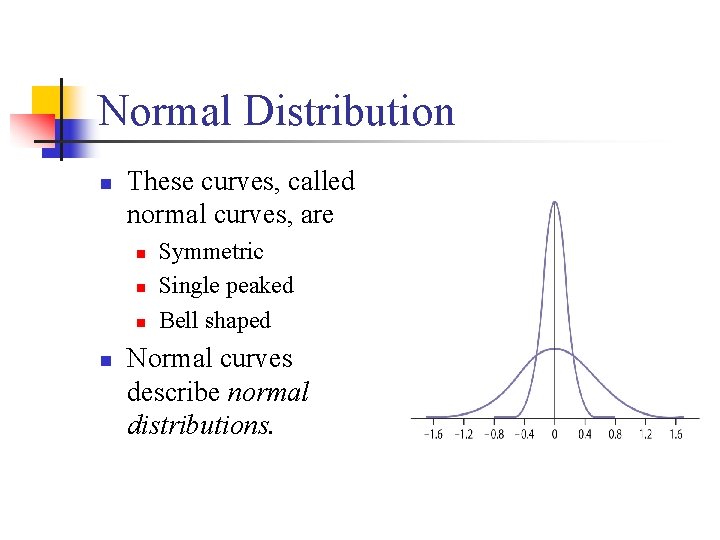
Normal Distribution n These curves, called normal curves, are n n Symmetric Single peaked Bell shaped Normal curves describe normal distributions.

Normal Density Curve n n n The exact density curve for a particular normal distribution is described by giving its mean and its standard deviation . The mean is located at the center of the symmetric curve and it is the same as the median. The standard deviation controls the spread of a normal curve.
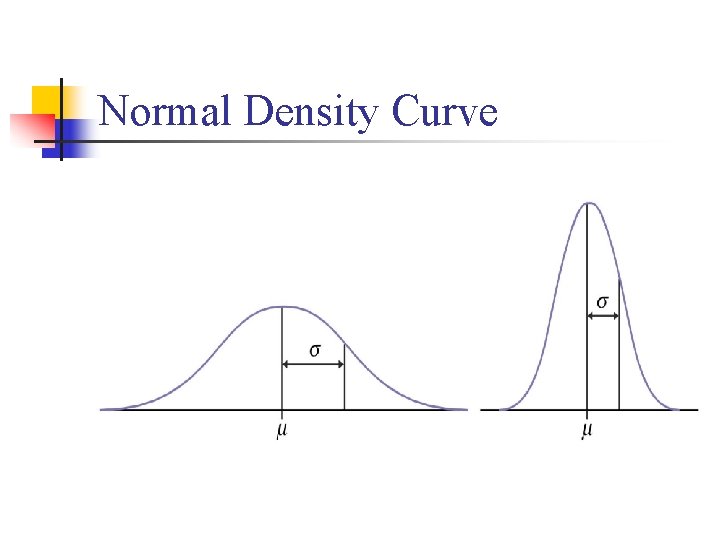
Normal Density Curve
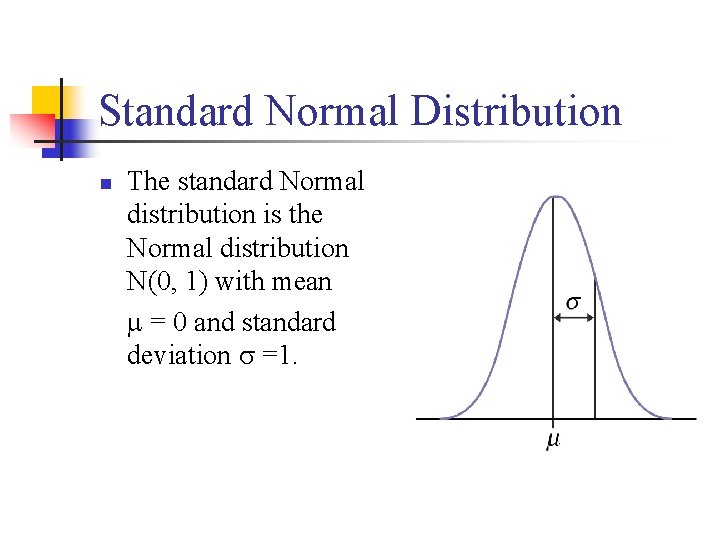
Standard Normal Distribution n The standard Normal distribution is the Normal distribution N(0, 1) with mean = 0 and standard deviation =1.

Standard Normal Distribution n If a variable x has any normal distribution N( , ) with mean and standard deviation , then the standardized variable has the standard Normal distribution.
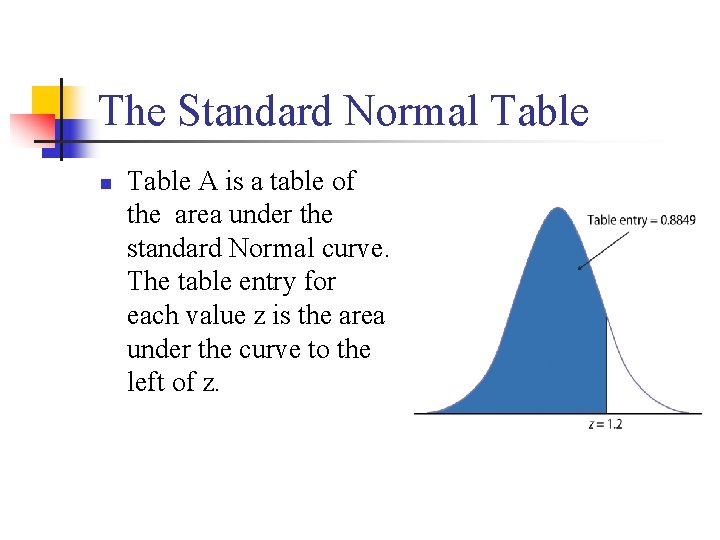
The Standard Normal Table n Table A is a table of the area under the standard Normal curve. The table entry for each value z is the area under the curve to the left of z.

The Standard Normal Applet n Or you can use this applet http: /www. stat. sc. edu~west/applets/normaldemo. html
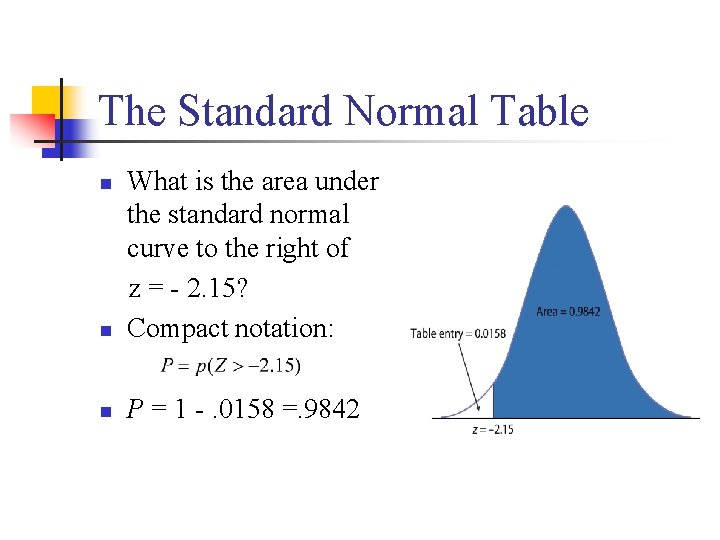
The Standard Normal Table n What is the area under the standard normal curve to the right of z = - 2. 15? Compact notation: n P = 1 -. 0158 =. 9842 n
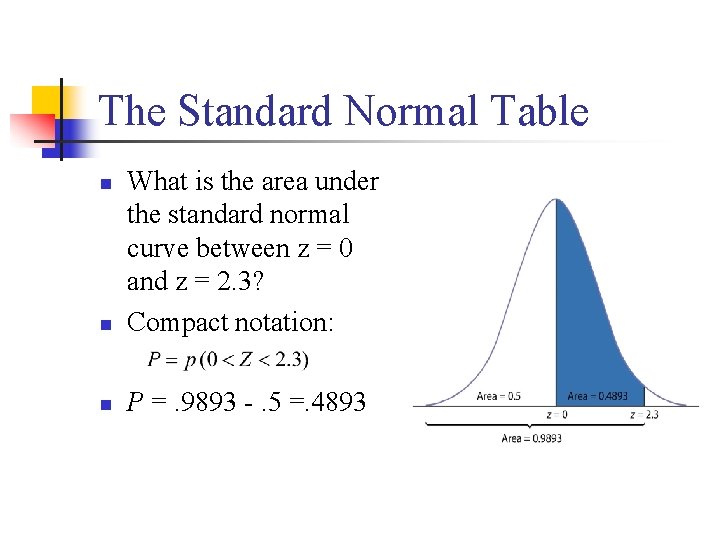
The Standard Normal Table n What is the area under the standard normal curve between z = 0 and z = 2. 3? Compact notation: n P =. 9893 -. 5 =. 4893 n

Example: Annual rate of return on stock indexes The annual rate of return on stock indexes (which combine many individual stocks) is approximately Normal. Since 1954, the Standard & Poor’s 500 stock index has had a mean yearly return of about 12%, with standard deviation of 16. 5%. Take this Normal distribution to be the distribution of yearly returns over a long period. The market is down for the year if the return on the index is less than zero. In what proportion of years is the market down?

Example: Annual rate of return on stock indexes n State the problem n n Call the annual rate of return for Standard & Poor’s 500 -stocks Index x. The variable x has the N(12, 16. 5) distribution. We want the proportion of years with X < 0. Standardize n Subtract the mean, then divide by the standard deviation, to turn x into a standard Normal z:
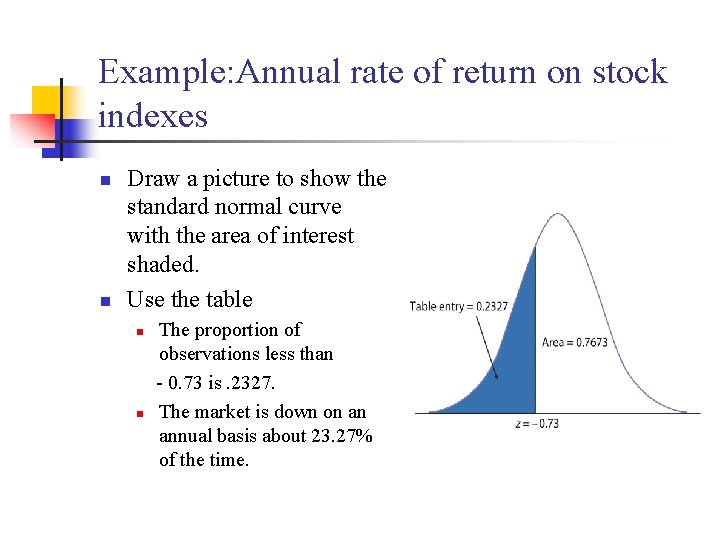
Example: Annual rate of return on stock indexes n n Draw a picture to show the standard normal curve with the area of interest shaded. Use the table n n The proportion of observations less than - 0. 73 is. 2327. The market is down on an annual basis about 23. 27% of the time.

Example: Annual rate of return on stock indexes n What percent of years have annual return between 12% and 50%? n State the problem n Standardize
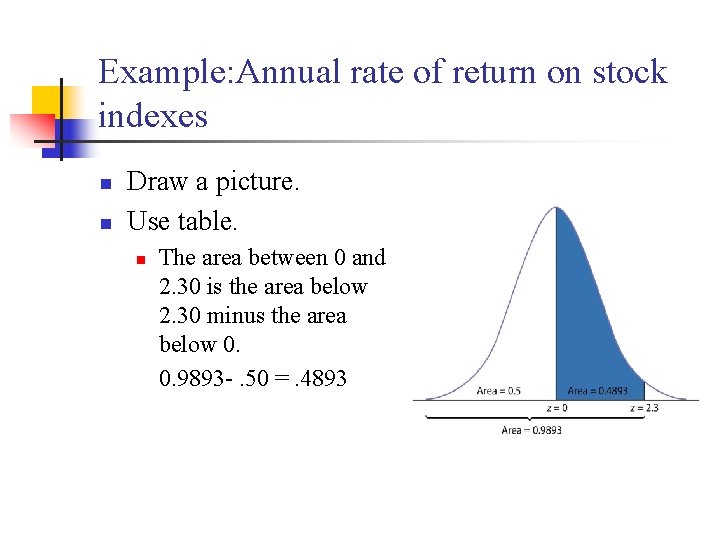
Example: Annual rate of return on stock indexes n n Draw a picture. Use table. n The area between 0 and 2. 30 is the area below 2. 30 minus the area below 0. 0. 9893 -. 50 =. 4893

Estimation n n So far, we have used our sample estimates as point estimates of parameters, for example: These estimators have properties.

Estimators n They are both unbiased estimators n The expected value of an unbiased estimator is equal to the parameter that it is trying to estimate.

Estimators n For Example: n It tends to give an answer that is a little too small.

Estimators n n n is also a minimum variance estimator of . This means that it has the smallest variability among all estimators of . What if we want to do more than just provide a point estimate?

Estimating with Confidence n Suppose we are interested in the value of some parameter, and we want to construct a confidence interval for it, with some desired level of confidence

Estimating with Confidence n n Suppose we can estimate this parameter from sample data, and we know the distribution of this estimator, then we can use this knowledge and construct a probability statement involving both the estimator and the true value of the parameter. This statement is manipulated mathematically to produce confidence intervals.

Confidence intervals n n The general form of a confidence interval is: sample value of estimator (Factor) (SE of estimator) The value of the factor will depend on the level of confidence desired, and the distribution of the estimator.

Estimating with Confidence n Community banks are banks with less than a billion dollars of assets. There approximately 7500 such banks in the United States. In many studies of the industry these banks are considered separately from banks that have more than a billion dollars of assets. The latter banks are called “large institutions. ” The community bankers Council of the American bankers Association (ABA) conducts an annual survey of community banks. For the 110 banks that make up the sample in a recent survey, the mean assets are = 220 (in millions of dollars). What can we say about , the mean assets of all community banks?

Estimating with Confidence n n The sample mean is the natural estimator of the unknown population mean . We know that n n is an unbiased estimator of . The law of large numbers says that the sample mean must approach the population mean as the size of the sample grows. Therefore, the value = 220 appears to be a reasonable estimate of the mean assets for all community banks. But, how reliable is this estimate?

Standard Error of Estimator n n n An estimate without an indication of its variability is of limited value. Questions about variation of an estimator is answered by looking at the spread of its sampling distribution. According to Central Limit theorem: n If the entire population of community bank assets has mean and standard deviation , then in repeated samples of size 110 the sample mean approximately follows the N( , 110) distribution

Standard Error of Estimator n Suppose that the true standard deviation is equal to the sample standard deviation s = 161. n n This is not realistic, although it will give reasonably accurate results for samples as large as 100. Later on we will learn how to proceed when is not known. Therefore, by Central Limit theorem. In repeated sampling the sample mean is approximately normal, centered at the unknown population mean , with standard deviation

Confidence Interval for the Population Mean n n We use the sampling distribution of the sample mean to construct a level C confidence interval for the mean of a population. We assume that data are a SRS of size n. The sampling distribution is exactly N( ) when the population has the N( , ) distribution. The Central Limit Theorem says that this same sampling distribution is approximately correct for large samples whenever the population mean and standard deviation are and .

Confidence Interval for a Population Mean n Choose a SRS of size n from a population having unknown mean and known standard deviation . A level C confidence interval for is Here z* is the critical value with area C between –z* and z* under the standard Normal curve. The quantity is the margin of error. The interval is exact when the population distribution is normal and is approximately correct when n is large in other cases.

Confidence Interval for a Population Mean n Recall the community bank Example n n What is a 90% confidence interval for the mean assets of all community banks? Estimator = Standard error of the sample mean = Factor =

Example: Banks’ loan –to-deposit ration n The ABA survey of community banks also asked about the loan-to-deposit ratio (LTDR), a bank’s total loans as a percent of its total deposits. The mean LTDR for the 110 banks in the sample is and the standard deviation is s = 12. 3. This sample is sufficiently large for us to use s as the population here. Find a 95% confidence interval for the mean LTDR for community banks.

Confidence Interval for a Population Mean n What if the sample size is small and the population standard deviation is not known? n n n Then the sampling distribution of will be student’s t. The Student’s t distribution has a symmetric, bellshaped density centered at zero, and depends on a parameter called the degrees of freedom. The number of degrees of freedom depends upon the sample size.

Students’ T Distribution n n The density of the Student’s t distribution differs from that of the standard normal density. The distribution of the density in the tails and flanks is different from the normal distribution: n The tails are higher and wider than that of a standard normal density, indicating that the standard deviation is larger than the standard normal, especially for small sample sizes. 0
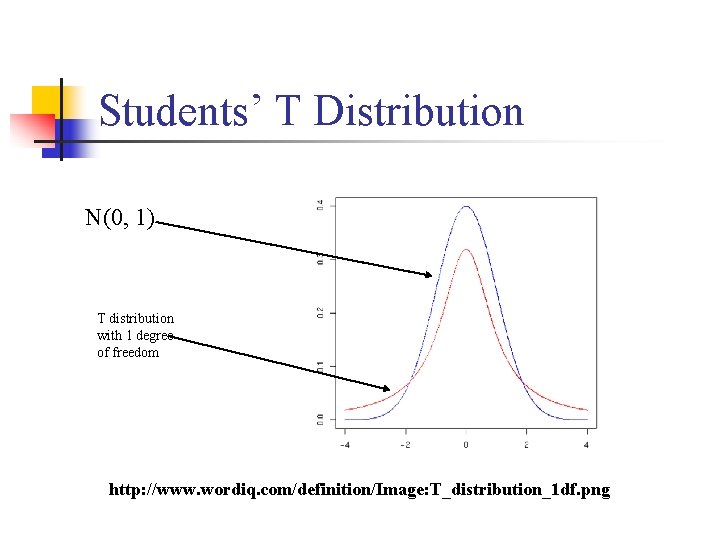
Students’ T Distribution N(0, 1) T distribution with 1 degree of freedom http: //www. wordiq. com/definition/Image: T_distribution_1 df. png

Students’ T Distribution n n As the sample size becomes larger, the degrees of freedom of the Student's t distribution also become larger. As the degrees of freedom become larger, the Student's t distribution approaches the standard normal distribution.
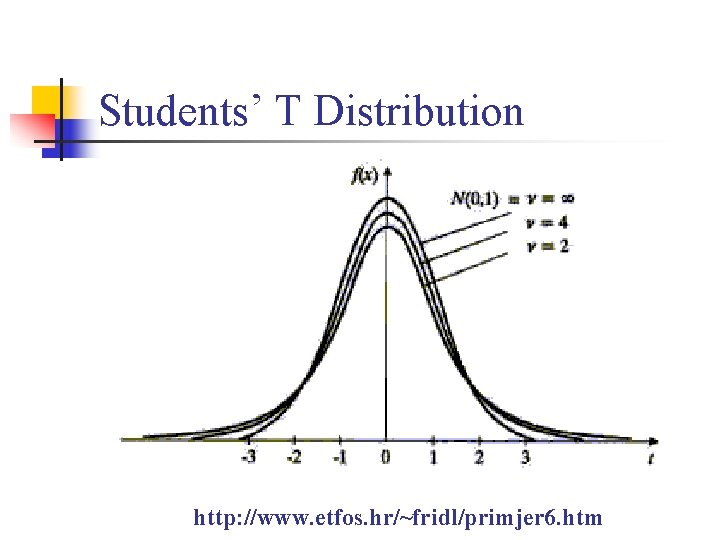
Students’ T Distribution http: //www. etfos. hr/~fridl/primjer 6. htm

Students’ T Distribution n A level C confidence interval for when the sample size is small and the population standard deviation is not known is: n n The t-distribution has n-1 degrees of freedom. Given the confidence level. the value can be determined from published tables for t-distribution.

Students’ T Distribution n Example: n If the sample size is 15, the critical value for a 95% confidence interval from a t-table is: 2. 14. n n Note the degrees of freedom is 14. If the sample size is 25, what is the critical value for a 90% confidence interval?

Tests of Significance n n n Confidence intervals are appropriate when our goal is to estimate a population parameter. The second type of inference is directed at assessing the evidence provided by the data in favor of some claim about the population. A significance test is a formal procedure for comparing observed data with a hypothesis whose truth we want to assess. The hypothesis is a statement about the parameters in a population or model. The results of a test are expressed in terms of a probability that measures how well the data and the hypothesis agree.

Example: Bank’s net income n The community bank survey described in previously also asked about net income and reported the percent change in net income between the first half of last year and the first half of this year. The mean change for the 110 banks in the sample is Because the sample size is large, we are willing to use the sample standard deviation s = 26. 4% as if it were the population standard deviation . The large sample size also makes it reasonable to assume that is approximately normal.

Example: Bank’s net income n n n Is the 8. 1% mean increase in a sample good evidence that the net income for all banks has changed? The sample result might happen just by chance even if the true mean change for all banks is = 0%. To answer this question we ask another n n Suppose that the truth about the population is that = 0% (this is our hypothesis) What is the probability of observing a sample mean at least as far from zero as 8. 1%?

Example: Bank’s net income n The answer is: n n n Because this probability is so small, we see that the sample mean is incompatible with a population mean of = 0. We conclude that the income of community banks has changed since last year.

Example: Bank’s net income n The fact that the calculated probability is very small leads us to conclude that the average percent change in income is not in fact zero. Here is why. n n If the true mean is = 0, we would see a sample mean as far away as 8. 1% only six times per 10000 samples. So there are only two possibilities: n n = 0 and we have observed something very unusual, or is not zero but has some other value that makes the observed data more probable

Example: Bank’s net income n n We calculated a probability taking the first of these choices as true ( = 0 ). That probability guides our final choice. If the probability is very small, the data don’t fit the first possibility and we conclude that the mean is not in fact zero.

Tests of Significance: Formal details n n The first step in a test of significance is to state a claim that we will try to find evidence against. Null Hypothesis H 0 n n n The statement being tested in a test of significance is called the null hypothesis. The test of significance is designed to assess the strength of the evidence against the null hypothesis. Usually the null hypothesis is a statement of “no effect” or “no difference. ” We abbreviate “null hypothesis” as H 0.

Tests of Significance: Formal details n A null hypothesis is a statement about a population, expressed in terms of some parameter or parameters. n n The null hypothesis in our bank survey example is H 0 : = 0 It is convenient also to give a name to the statement we hope or suspect is true instead of H 0. This is called the alternative hypothesis and is abbreviated as Ha. In our bank survey example the alternative hypothesis states that the percent change in net income is not zero. We write this as Ha : 0

Tests of Significance: Formal details n n n Since Ha expresses the effect that we hope to find evidence for we often begin with Ha and then set up H 0 as the statement that the Hoped-for effect is not present. Stating Ha is not always straight forward. It is not always clear whether Ha should be one-sided or two-sided. n The alternative Ha : 0 in the bank net income example is two-sided. n In any give year, income may increase or decrease, so we include both possibilities in the alternative hypothesis.

Tests of Significance: Formal details n Test statistics n We will learn the form of significance tests in a number of common situations. Here are some principles that apply to most tests and that help in understanding the form of tests: n n The test is based on a statistic that estimate the parameter appearing in the hypotheses. Values of the estimate far from the parameter value specified by H 0 gives evidence against H 0.

Example: bank’s income n The test statistic n n In our banking example The null hypothesis is H 0: = 0, and a sample gave the. The test statistic for this problem is the standardized version of : This statistic is the distance between the sample mean and the hypothesized population mean in the standard scale of z-scores.

Example: Bank’s net income n p-values n n P-value is the probability that the test statistic would take a value as large or larger than one observed assuming that H 0 is true. The smaller the p-value, the stronger the evidence against H 0.

Example: Bank’s net income n Conclusion n n One approach is to state in advance how much evidence against H 0 we will require in order to reject it. The level that says “this evidence is strong enough “ is called significance level and is denoted by letter . We compare the p-value with the significance level. We reject H 0 if the p-value is smaller than the significance level, and say that the data are statistically significant at level .

One sample t-test n n n Suppose we have a simple random sample of size n from a Normally distributed population with mean and standard deviation . The standardized sample mean, or one-sample z statistic has the standard Normal distribution N(0, 1). When we substitute the standard deviation of the mean (standard error) s / n for the / n, the statistic does not have a Normal distribution.

The t-distribution n t-test n Suppose that a SRS of size n is drawn from a N( , ) population. Then the one sample t statistic has the t-distribution with n-1 degrees of freedom. n There is a different t distribution for each sample size. n A particular t distribution is specified by giving the degrees of freedom.

Exploring Relationships between Two Quantitative Variables n Scatter plots n n Represent the relationship between two different continuous variables measured on the same subjects. Each point in the plot represents the values for one subject for the two variables.
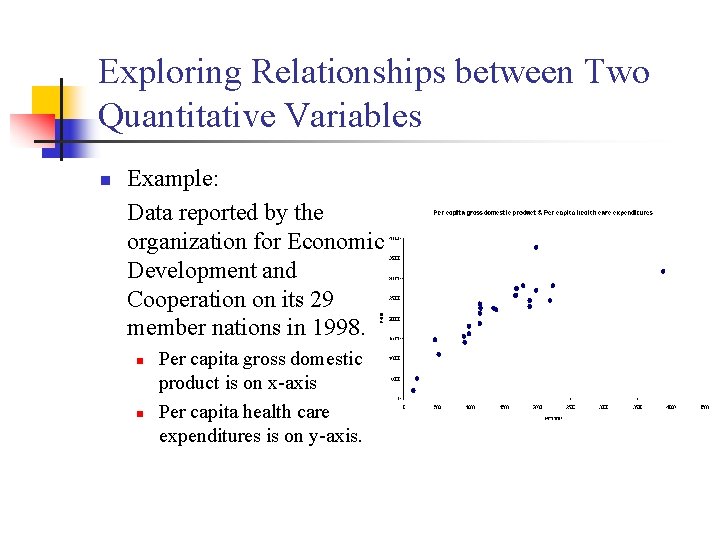
Exploring Relationships between Two Quantitative Variables n Example: Data reported by the organization for Economic Development and Cooperation on its 29 member nations in 1998. n n Per capita gross domestic product is on x-axis Per capita health care expenditures is on y-axis.

Exploring Relationships between Two Quantitative Variables n We can describe the overall pattern of scatter plot by n n n Form or shape Direction strength

Exploring Relationships between Two Quantitative Variables n Form or shape n n The form shown by the scatter plot is linear if the points lie in a straight-line pattern. Strength n The relation ship is strong if the points lie close to a line, with little scatter.

Exploring Relationships between Two Quantitative Variables n Direction n Positive and negative association n n Two variables are positively associated when aboveaverage values of one variable tend to occur in individuals with above average values for the other variable, and below average values of both also tend to occur together. Two variable are negatively associated when above average values for one tend to occur in subjects with below average values of the other, and vice-versa
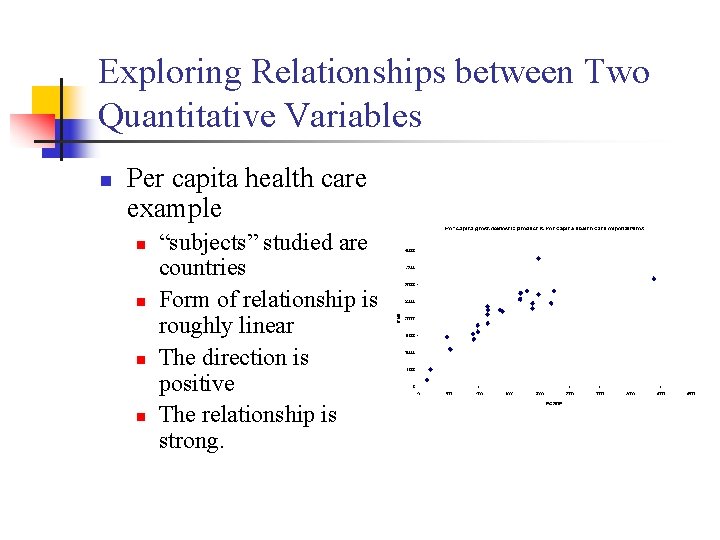
Exploring Relationships between Two Quantitative Variables n Per capita health care example n n “subjects” studied are countries Form of relationship is roughly linear The direction is positive The relationship is strong.

Correlation n It is often useful to have a measure of degree of association between two variables. For example, you may believe that sales may be affected by expenditures on advertising, and want to measure the degree of association between sales and advertising. n n Correlation coefficient is a numeric measure of the direction and strength of linear relationship between two continuous variables The notation for sample correlation coefficient is r.

Correlation n There are several alternative ways to write the algebraic expression for the correlation coefficient. The following is one. n n n X and Y represent the two variables of interest. For example advertising and sales or per capita gross domestic product, and per capita health care expenditure. n is the number of subjects in the sample The notation for population correlation coefficient is .

Correlation n Facts about correlation coefficient n n n r has no unit. r > 0 indicates a positive association; r < 0 indicates a negative association r is always between – 1 and +1 Values of r near 0 imply a very weak linear relationship Correlation measures only the strength of linear association.

Correlation n n We could perform a hypothesis test to determine whether the value of a sample correlation coefficient (r) gives us reason to believe that the population correlation ( ) is significantly different from zero The hypothesis test would be H 0: = 0 Ha : 0

Correlation n The test statistic would be n n The test statistic has a t-distribution with n-2 degrees of freedom. Reject H 0 if

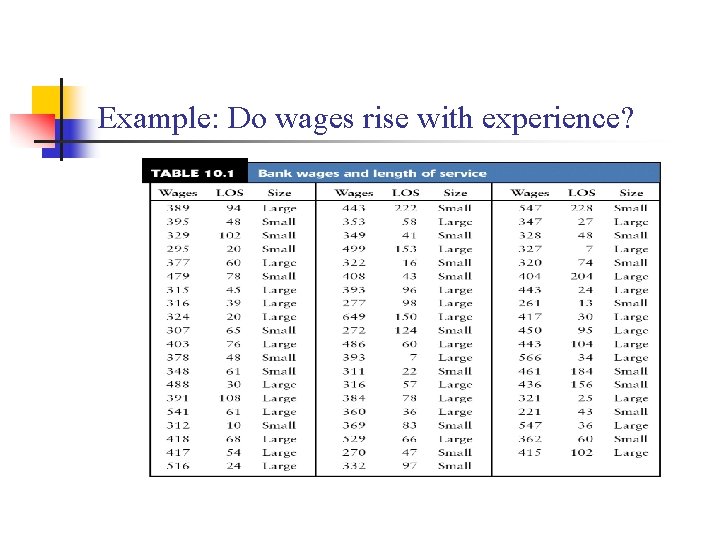
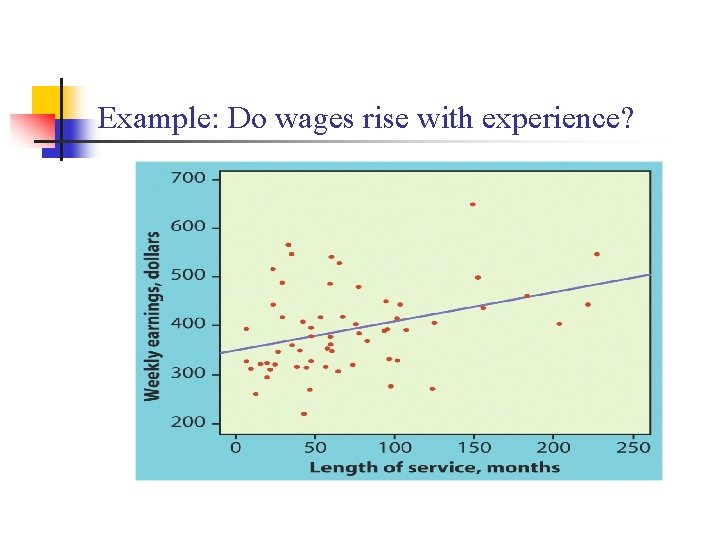
Example: Do wages rise with experience? n Many factors affect the wages of workers: the industry they work in, their type of job, their education and their experience, and changes in general levels of wages. We will look at a sample of 59 married women who hold customer service jobs in Indiana banks. The following table gives their weekly wages at a specific point in time also their length of service with their employer, in month. The size of the place of work is recorded simply as “large” (100 or more workers) or “small. ” Because industry, job type, and the time of measurement are the same for all 59 subjects, we expect to see a clear relationship between wages and length of service.
Example: Do wages rise with experience?
Example: Do wages rise with experience?

Example: Do wages rise with experience? n n The correlation between wages and length of service for the 59 bank workers is r = 0. 3535. We expect a positive correlation between length of service and wages in the population of all married female bank workers. Is the sample result convincing that this is true?

Example: Do wages rise with experience? n To compute correlation: we need: n Replacing these in the formula n We want to test H 0: = 0 The test statistic is Ha : > 0

Example: Do wages rise with experience? n n Comparing t = 2. 853 with critical values from the t-table with n - 2 = 57 degrees of freedom help us to make our decision. Conclusion: n n Since P( t > 2. 853) <. 005, we reject H 0. There is a positive correlation between wages and length of service.

T-distribution applet n Tail probability for student’s t-distribution can computed using the applet at the following site. http: //www. acs. ucalgary. ca/~nosal/src/Applets/T-Tail. Prob. html
- Slides: 97