Review of Basic Principle of Thermodynamics 1 1

Review of Basic Principle of Thermodynamics 1 1. Properties of Pure Substances 2. Heat and Work 3. 1 st Law for Closed Systems 4. 1 st Law for Control Volumes 5. 2 nd Law of Thermodynamics 6. Entropy Assoc. Prof. Sommai Priprem, Ph. D. Faculty of Engineering Khon Kaen University ��. ������� 1

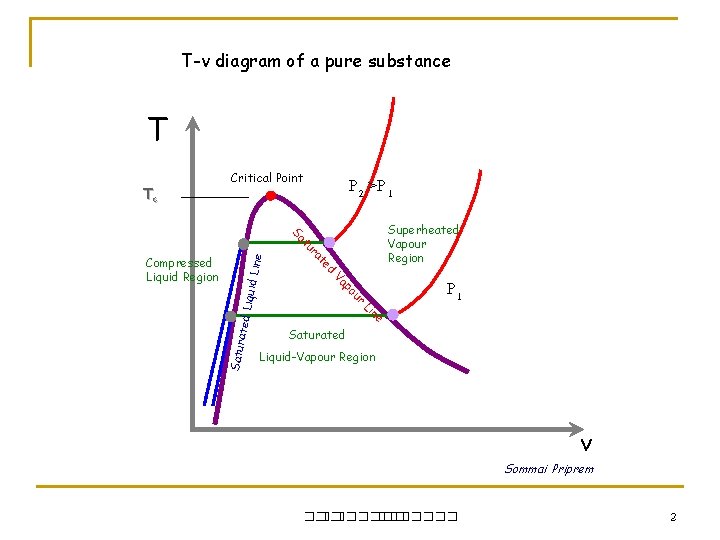
T-v diagram of a pure substance T Tc P 2 >P 1 Critical Point iquid L ine e n Li ated L r ou Satur P 1 p Va Compressed Liquid Region d te ra tu Sa Superheated Vapour Region Saturated Liquid-Vapour Region v Sommai Priprem ��. ������� 2

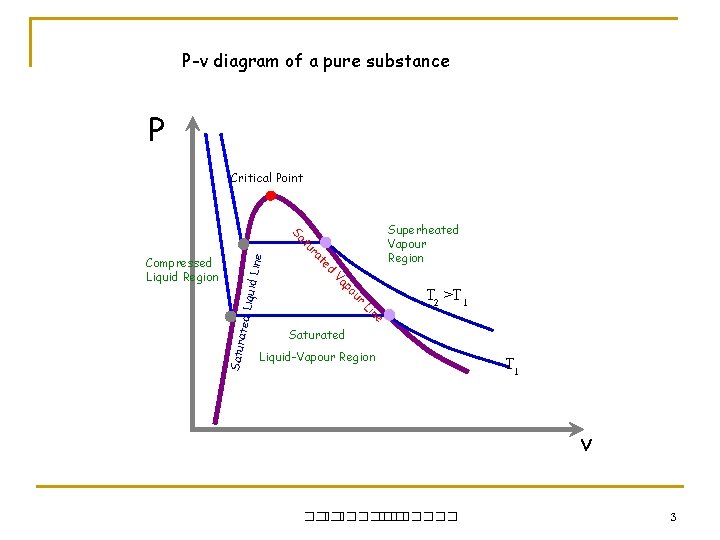
P-v diagram of a pure substance P Critical Point iquid L ine ated L T 2 >T 1 e n Li Satur r ou p Va Compressed Liquid Region d te ra tu Sa Superheated Vapour Region Saturated Liquid-Vapour Region T 1 v ��. ������� 3

Thermodynamics Table n n n Properties Relationship are too COMPLEX Not simple EQUATIONS can be represented Therefore, TABLEs are more convenion Each substance; more than one table, Each table for each REGION ie. ; q Compressed Liquid q Saturated Liquid and Saturated Vapour q Superheated Vapour (2 = T table & P table) No table for Mixture Calculate using Saturated Table + x ��. ������� 4

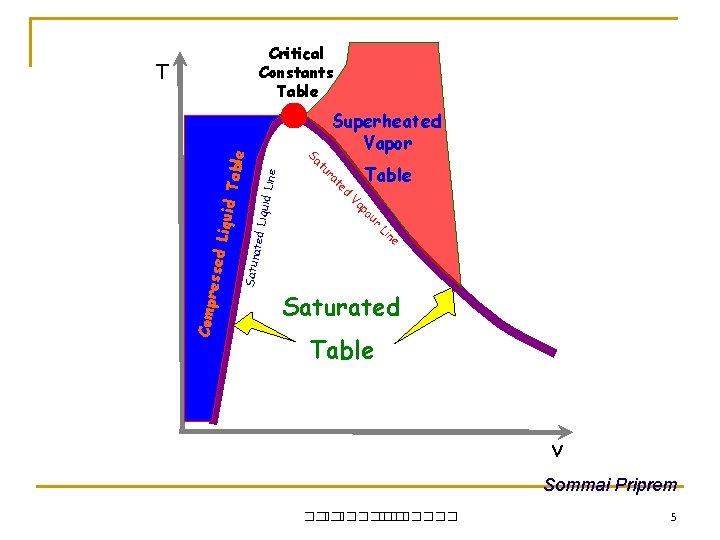
Critical Constants Table Superheated Vapor ine iquid L ur po Va Satur e n Li ated L Table ed Compr e t ra tu Sa ssed L iquid T able T Saturated Table v Sommai Priprem ��. ������� 5

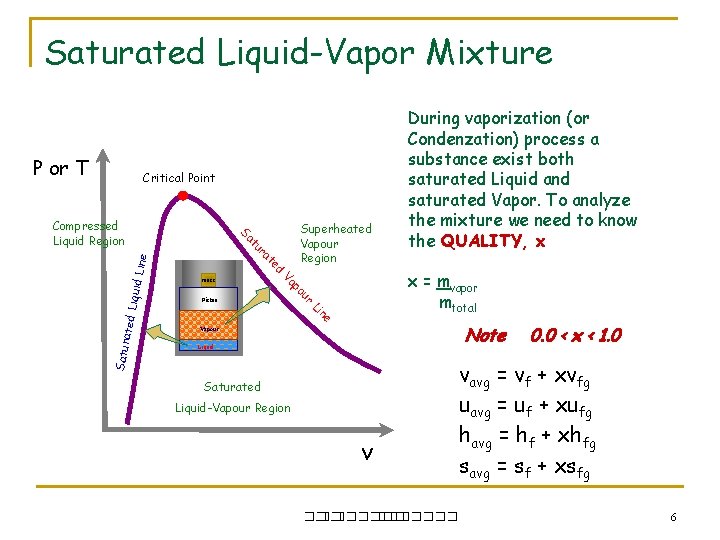
Saturated Liquid-Vapor Mixture P or T Critical Point iquid L ine Piston r Vapour e n Li ated L x = mvapor mtotal ou Satur Superheated Vapour Region p Va mass d te ra tu Sa Compressed Liquid Region During vaporization (or Condenzation) process a substance exist both saturated Liquid and saturated Vapor. To analyze the mixture we need to know the QUALITY, x Note Liquid Saturated Liquid-Vapour Region v ��. ������� 0. 0 < x < 1. 0 vavg = vf + xvfg uavg = uf + xufg havg = hf + xhfg savg = sf + xsfg 6

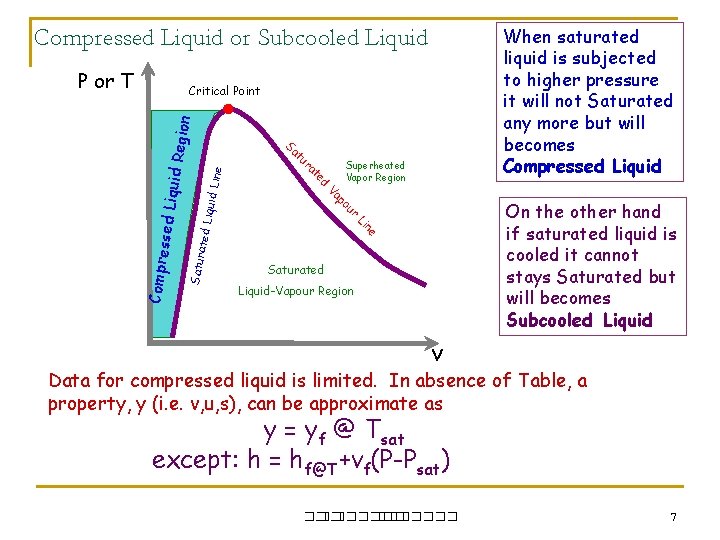
When saturated liquid is subjected to higher pressure it will not Saturated any more but will becomes Compressed Liquid or Subcooled Liquid P or T ne Li iquid L ine ated L r Satur On the other hand if saturated liquid is cooled it cannot stays Saturated but will becomes Subcooled Liquid u po ssed Li Superheated Vapor Region Va Compre ed t ra tu Sa quid Re gion Critical Point Saturated Liquid-Vapour Region v Data for compressed liquid is limited. In absence of Table, a property, y (i. e. v, u, s), can be approximate as y = yf @ Tsat except: h = hf@T+vf(P-Psat) ��. ������� 7

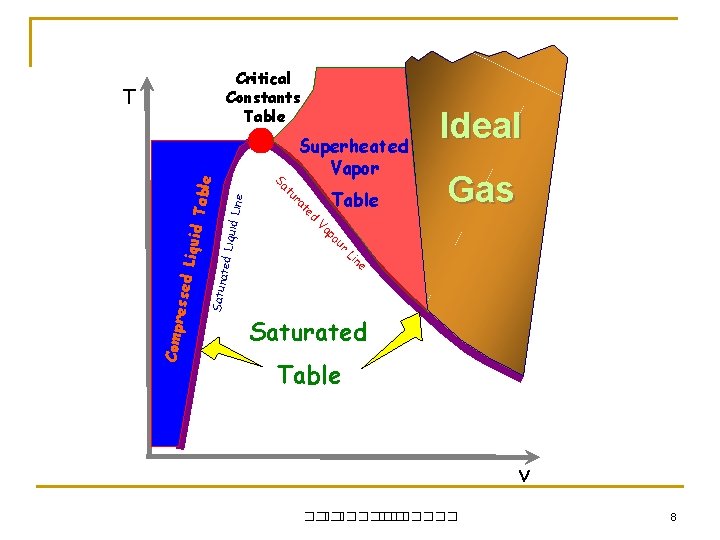
Critical Constants Table ine Gas ur po Va iquid L Table Ideal ed e n Li Satur ated L t ra tu Compr e Superheated Vapor Sa ssed L iquid T able T Saturated Table v ��. ������� 8

Ideal Gas n n n Pv =RT ideal gas equation of state R = Ru/M k. J/kg-K Ru = Universal gas constant = 8. 3143 k. J/kmol-K = 1. 868 Btu/lbmol-R = 1545 ft-lbf/lbmol-R n n n M = Molecular weight of the gas, kg/k. Mol m = n. M n = number of mole of the gas ��. ������� 9

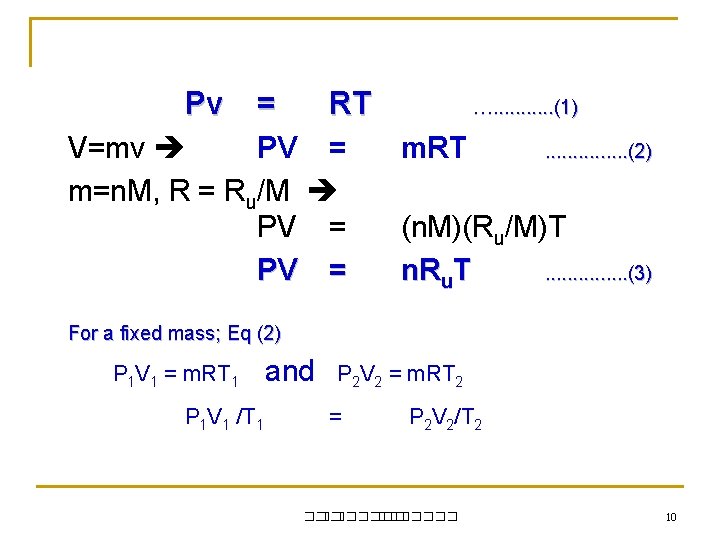
Pv = RT V=mv PV = m=n. M, R = Ru/M PV = …. . . (1) m. RT . . . . (2) (n. M)(Ru/M)T n. Ru. T. . . . (3) For a fixed mass; Eq (2) P 1 V 1 = m. RT 1 P 1 V 1 /T 1 and P 2 V 2 = m. RT 2 = P 2 V 2/T 2 ��. ������� 10

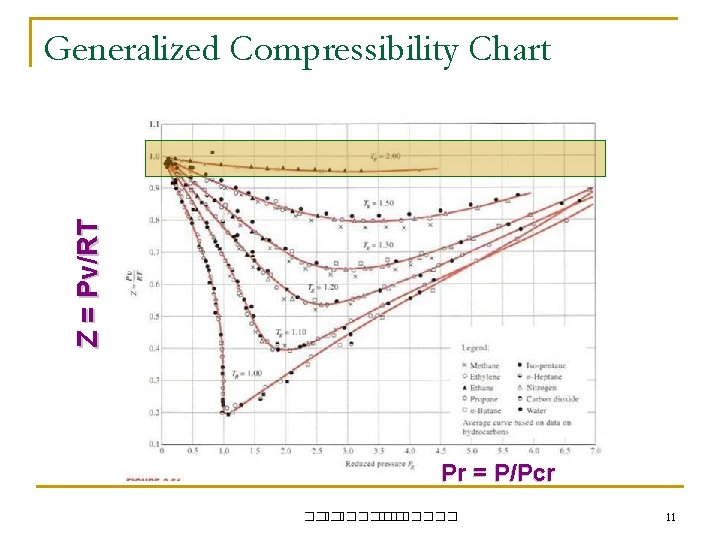
Z = Pv/RT Generalized Compressibility Chart Pr = P/Pcr ��. ������� 11

Compressibility Factor, Z– A measure of Deviation from Ideal-Gas Behavior Z = Pv/RT n Pr = P/Pcr = reduced pressure n Tr = T/Tcr = reduced temperature Conclusion from the chart n at low P; Pr << 1; good to assume ideal gas regardless of T n n at high T; Tr > 2 ; good to assume ideal gas (except when Pr >> 1) Near Critcal Point ; Greatest deviation from ideal gas behavior ��. ������� 12

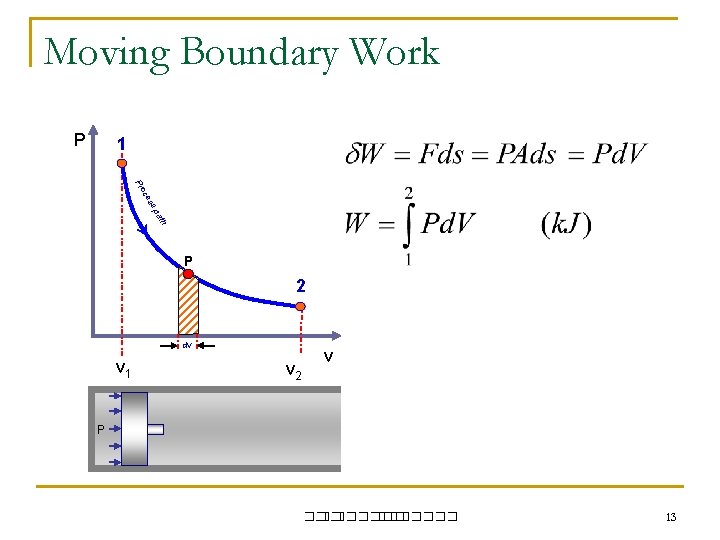
Moving Boundary Work P 1 s es oc Pr th pa P 2 dv v 1 v 2 v P ��. ������� 13

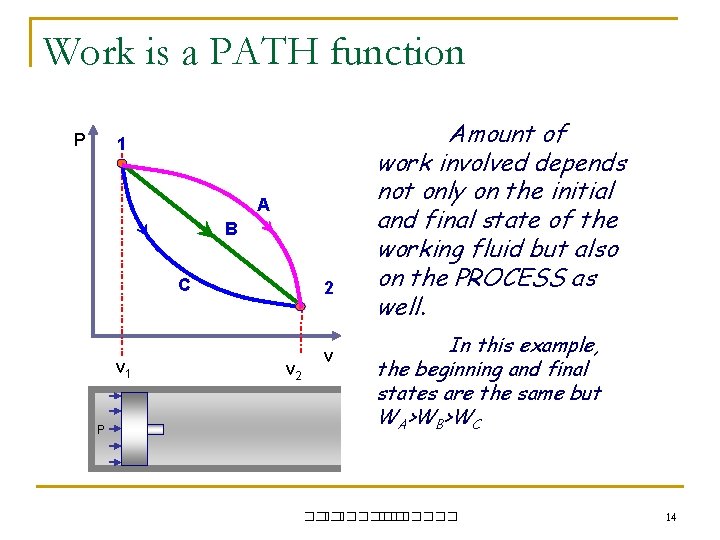
Work is a PATH function P 1 A B C v 1 P 2 v Amount of work involved depends not only on the initial and final state of the working fluid but also on the PROCESS as well. In this example, the beginning and final states are the same but WA>WB>WC ��. ������� 14

Specific Heat is defined as “the energy required to raise the temperature of a unit mass of a substance by one degree. ” For fluids there are two different specific heat: • Specific heat at constant volume, • • Specific heat at constant pressure, ��. ������� 15

Internal Energy, Enthalpy, and Specific Heat of Ideal Gases Sp. Heat @ v; Sp. Heat @ p; du = Cvd. T dh = Cpd. T ��. ������� 16

To determine Δu and Δh of Ideal Gases 3 - Ways Δu = u 2 – u 1 (Table) Δu = Cv, avΔT Δh similar ways ��. ������� 17

Conclusion of Importance Equations of Chapter 3 Boundary Work; w =∫ Pdv . . . (1) 1 st Law general ΣEin - ΣEout = ΔE Closed System; . . . . (2) Q – W = ΔU + ΔKE + ΔPE . . . . (3) Enthalpy (defined) h = u + Pv . . . (4) Specific Heat: du = Cvd. T . . . (5) dh = Cpd. T . . . (6) Cp = Cv + R . . . (7) k . . . (8) for Ideal gases: = Cp/Cv ��. ������� 18

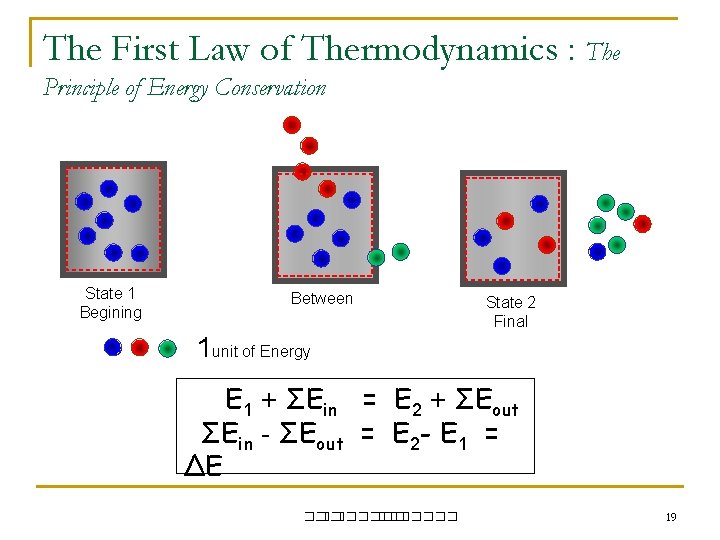
The First Law of Thermodynamics : The Principle of Energy Conservation State 1 Begining Between State 2 Final 1 unit of Energy E 1 + ΣEin = E 2 + ΣEout ΣEin - ΣEout = E 2 - E 1 = ΔE ��. ������� 19

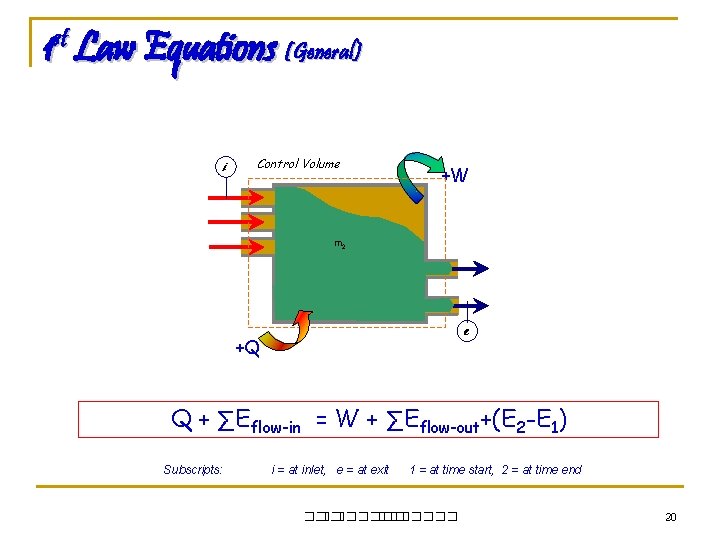
1 st Law Equations (General) i Control Volume +W m 2 m 1 e +Q Q + ∑Eflow-in = W + ∑Eflow-out+(E 2 -E 1) Subscripts: i = at inlet, e = at exit 1 = at time start, 2 = at time end ��. ������� 20

Total Energy of Fluid n n for non-flow mass inside control volume (cv) q enonflow = u +ke + pe k. J/kg 2 + zg ) q E nonflow = m(u + ½ V J for flowing fluid mass flowing in/out of cv. q q q eflow = enonflow+ flow work eflow = u + Pv + ke + pe defined: h = u + Pv eflow = h +ke + pe k. J/kg Eflow = m(h + ½ V 2 + zg ) J ��. ������� 21

Sign Convention of HEAT and WORK Heat Engine System Model Add heat to system, Qin System gives WORK, Wout +Q +W ��. ������� 22

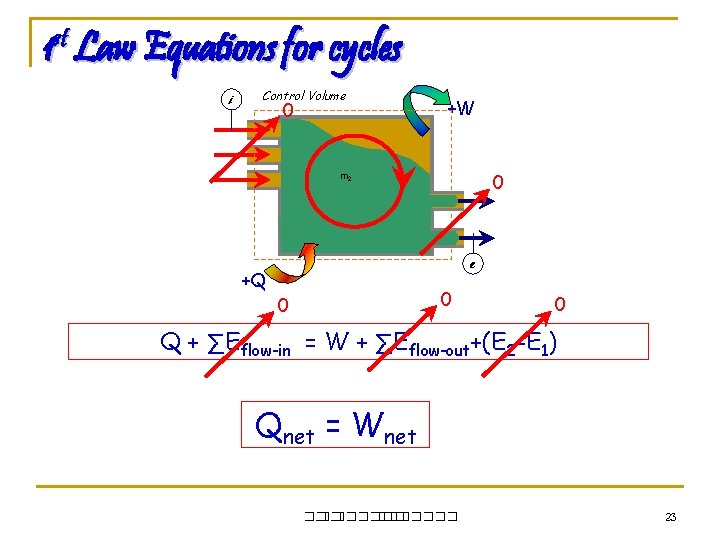
1 st Law Equations for cycles i Control Volume 0 +W 0 m 2 m 1 e +Q 0 0 0 Q + ∑Eflow-in = W + ∑Eflow-out+(E 2 -E 1) Qnet = Wnet ��. ������� 23

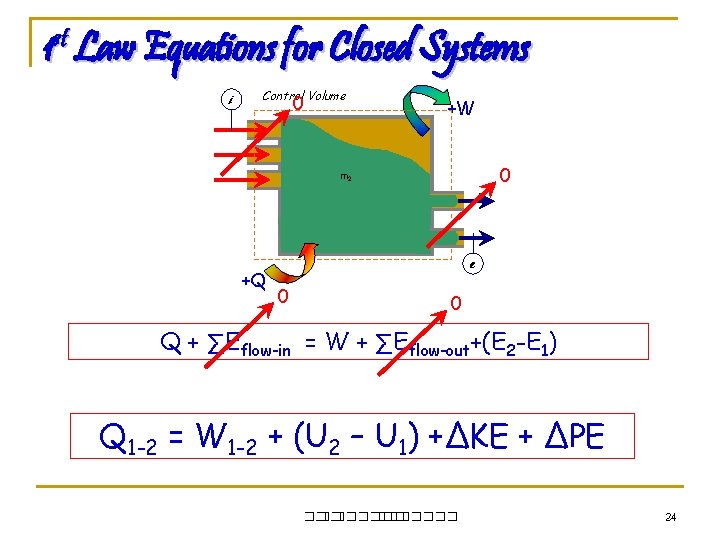
1 st Law Equations for Closed Systems i Control Volume 0 +W 0 m 2 m 1 +Q e 0 0 Q + ∑Eflow-in = W + ∑Eflow-out+(E 2 -E 1) Q 1 -2 = W 1 -2 + (U 2 – U 1) +∆KE + ∆PE ��. ������� 24

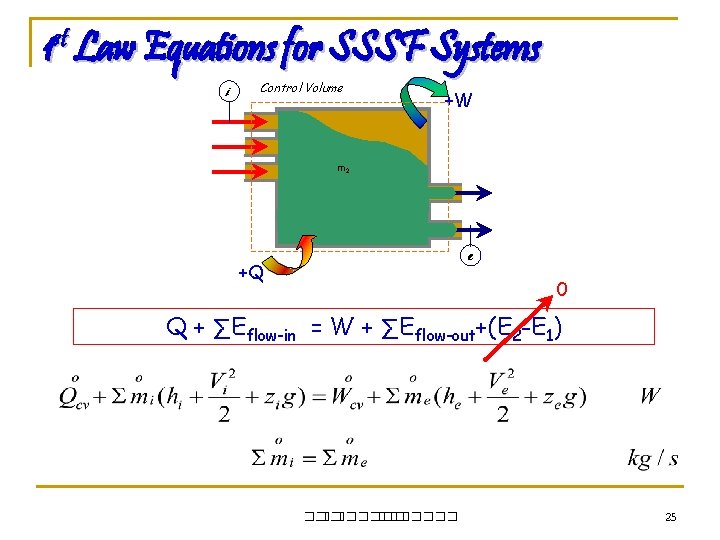
1 st Law Equations for SSSF Systems i Control Volume +W m 2 m 1 e +Q 0 Q + ∑Eflow-in = W + ∑Eflow-out+(E 2 -E 1) ��. ������� 25

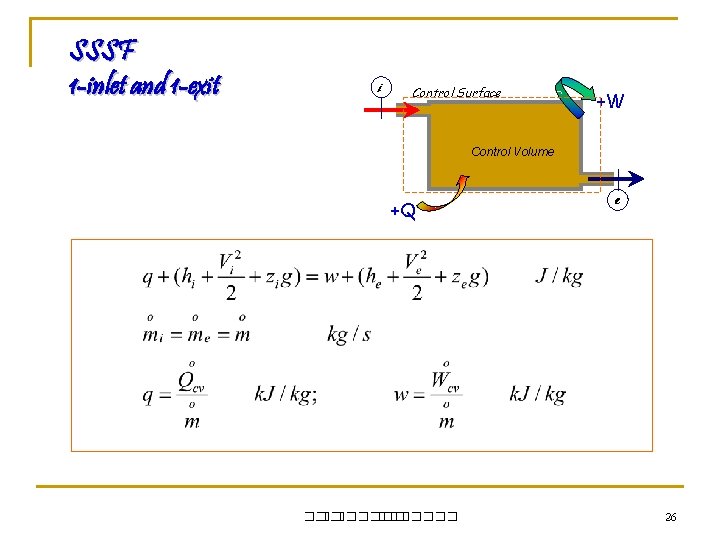
SSSF 1 -inlet and 1 -exit i Control Surface +W Control Volume +Q ��. ������� e 26

Chapter 5 2 nd Law of Thermodynamics Assoc. Prof. Sommai Priprem, Ph. D. Department of Mechanical Engineering Khon Kaen University ��. ������� 27

Summary n n n Processes occur in a certain direction, not in any direction. A process will not occur unless it satisfy both 1 st and 2 nd law. Importance Definitions: q q q Thermal Reservoir; Source, Sink Thermal Efficiency and Heat Engine Coefficient of Performance and Heat Pump Reversible Process and Irreversible Process Carnot cycle and Carnot Principles ��. ������� 28

Thermal Efficiency Performance = desired output required input (5. 1) = net work output total heat input (5. 2) Heat engine: Thermal efficiency Source, TH QH Heat Engine Wnet QL Sink, TL th = Wnet Qin (5. 3) th = 1 - QL QH (5. 4) QL and QH are magnitude (amount) of heat, their direction are already accounted for in the equation. ��. ������� 29

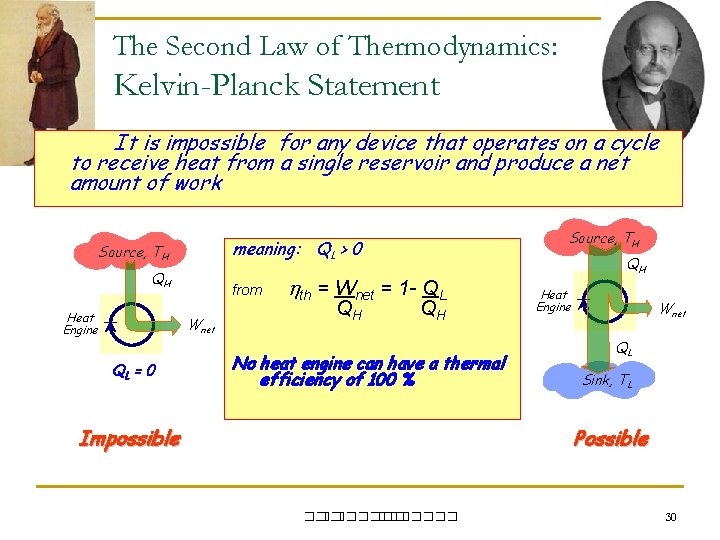
The Second Law of Thermodynamics: Kelvin-Planck Statement It is impossible for any device that operates on a cycle to receive heat from a single reservoir and produce a net amount of work Source, TH QH Heat Engine from Wnet QL = 0 Source, TH meaning: QL > 0 th = Wnet = 1 - QL QH QH No heat engine can have a thermal efficiency of 100 % Impossible QH Heat Engine Wnet QL Sink, TL Possible ��. ������� 30

The Second Law of Thermodynamics: Clausuis Statement It is impossible to construct a device that operates in a cycle and produces no effect other than the transfer of heat from a lower-temperature body to a highertemperature body. meaning: W > 0 High-Temp. Body, TH from Q Low-Temp. Body, TL COP = High-Temp. Body, TH Q W No heat pump can have a COP of QH Heat Pump W QL Low-Temp. Body, TL Possible Impossible ��. ������� 31

The Carnot Principles 1. 2. The efficiency of an irreversible heat engine is always less than the efficiency of a reversible one operating between the same two reservoirs. The efficiency of all reversible heat engines operating between the same two reservoirs are the same. High-temp. reservoir, TH 2 rev. HE 1 Irrev. HE th, 1 < th, 2 3 rev. HE th, 2 = th, 3 Low-temp. reservoir, TL ��. ������� 32

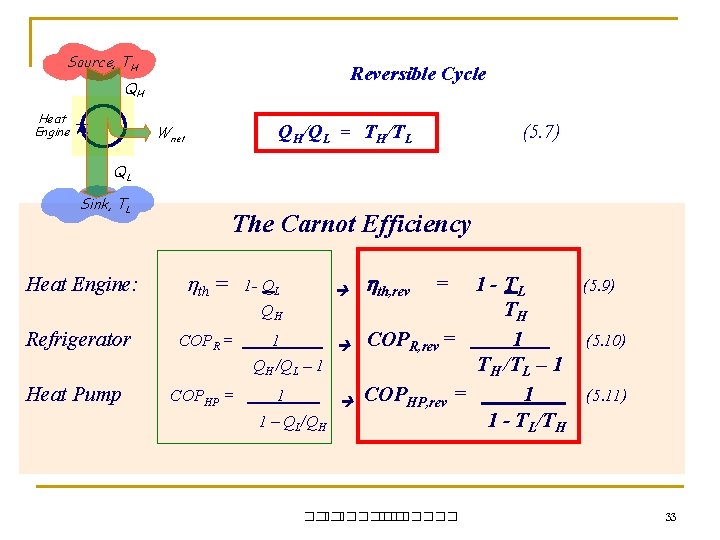
Source, TH Reversible Cycle QH Heat Engine QH/QL = TH/TL Wnet (5. 7) QL Sink, TL The Carnot Efficiency Heat Engine: th = Refrigerator COPR = 1 QH /QL – 1 Heat Pump COPHP = 1 1 – QL/QH 1 - QL QH th, rev = 1 - TL (5. 9) TH COPR, rev = 1 (5. 10) TH /TL – 1 COPHP, rev = 1 (5. 11) 1 - TL/TH ��. ������� 33

Chapter 6 ENTROPY ��. ������� 34

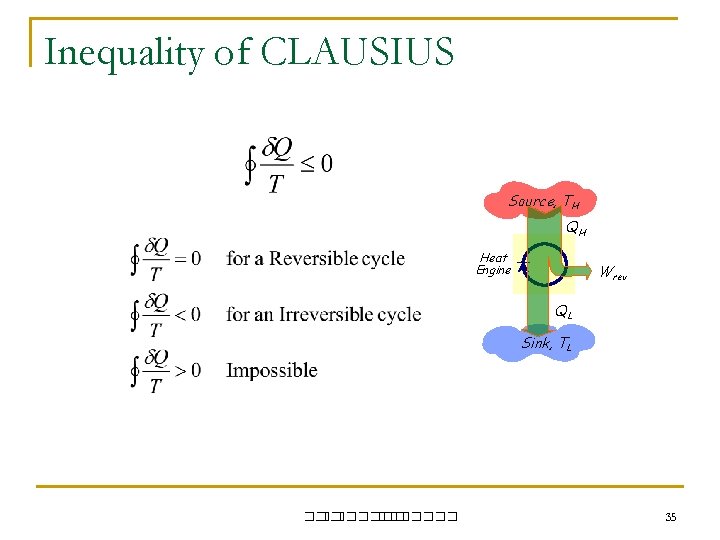
Inequality of CLAUSIUS Source, TH QH Heat Engine Wrev QL Sink, TL ��. ������� 35

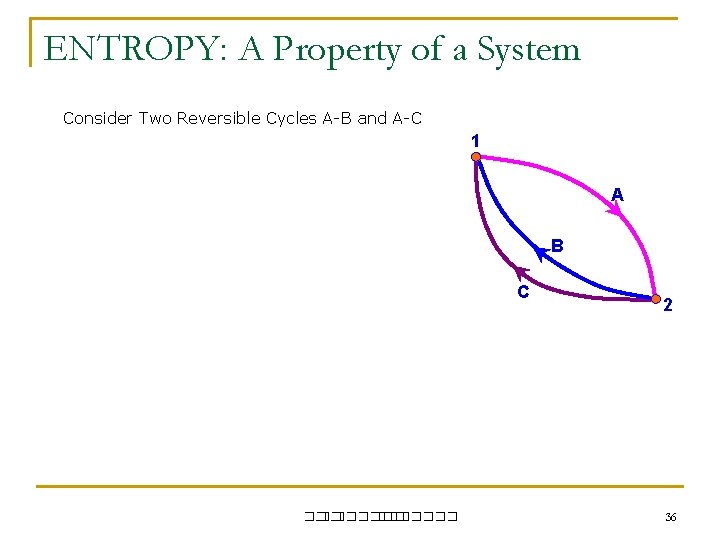
ENTROPY: A Property of a System Consider Two Reversible Cycles A-B and A-C 1 A B C ��. ������� 2 36

Two Important Thermodynamics Relations Consider a internally reversible CLOSED system; 1 st Law δQ = d. U + δW Td. S = d. U +Pd. V T ds = du + Pdv. . (6. 4) but h = u + Pv dh = du + d(Pv) dh = du + Pdv + vd. P substitute in (6. 4) Tds = dh – vd. P. . (6. 5) ��. ������� 37

Principle of Increase of Entropy Surroundings, temperature = T 0 Q System, temperature = T ��. ������� W 38

Entropy Change of a Solid or Liquid Solid & Liquid n Specific Heat = Constant n ΔV very small Δh~Δu ~ q n ds = ( Q/T)rev du/T Cd. T/T s 2 -s 1 C ln(T 2/T 1) ��. ������� 39

Entropy Change of an Ideal Gas ��. ������� 40

Isentropic Process of Ideal Gases ��. ������� 41

Reversible Polytropic Process of Ideal Gases ��. ������� 42

Second Law Efficiency ��. ������� 43