Review Normal Distributions Draw a picture Convert to

Review • Normal Distributions – Draw a picture. – Convert to standard normal (if necessary) – Use the binomial tables to look up the value. – In the case of a reverse look up we may have to now solve for x.

Estimator and Point Estimate An estimator is a “sample statistic” (such as the sample mean, or sample standard deviation) used to approximate a population parameter. A Point Estimate is a single value or point used to approximate a population parameter. A point estimator may be biased or unbiased.

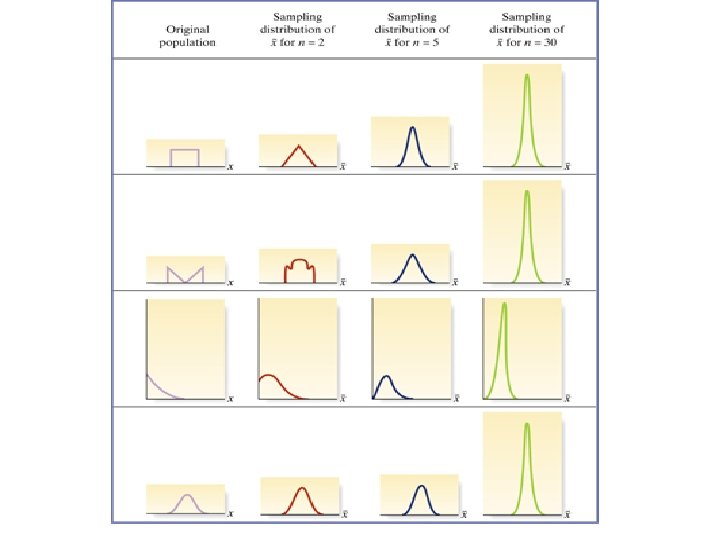
Central Limit Theorem Take ANY random variable X and compute and for this variable. If samples of size n are randomly selected from the population, then: 1) For large n, the distribution of the sample means, will be approximately a normal distribution, 2) The mean of the sample means will be the population mean and 3) The standard deviation of the sample means will be
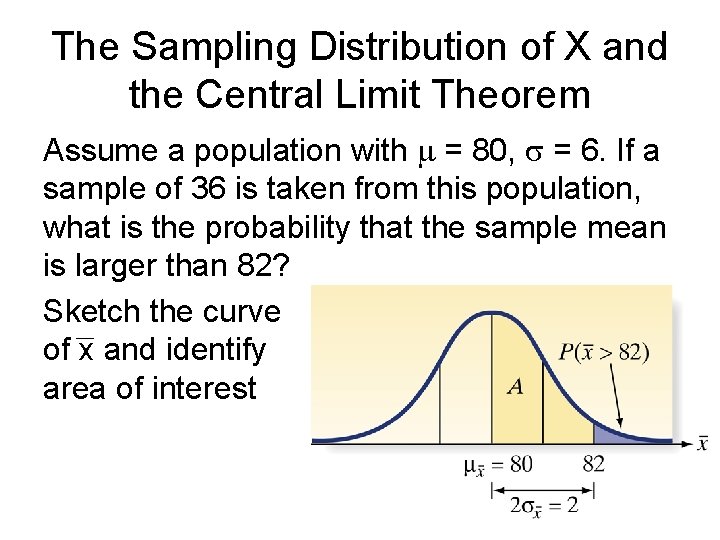
The Sampling Distribution of X and the Central Limit Theorem Assume a population with = 80, = 6. If a sample of 36 is taken from this population, what is the probability that the sample mean is larger than 82? Sketch the curve of x and identify area of interest

The Sampling Distribution of X and the Central Limit Theorem Convert 82 to z value First, calculate the standard deviation of the sampling distribution Then calculate the z value Use the tables to find probability of interest

Practice Problems • #6. 34 page 310 • #6. 41 page 311

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. What can you say about the average balance?

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. What can you say about the average balance of all VISA accounts? ANS: That it is approximately $213. (This is a point estimate.

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. If in addition you know the standard deviation for all accounts is $112, what can you say about the average balance of all VISA accounts?

Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. If in addition you know the standard deviation for all accounts is $112, what can you say about the average balance of all VISA accounts? You can create an interval (called a confidence interval) that you can be 95% sure the mean is in.

Confidence Interval A confidence interval (or interval estimate) is a range of values that estimates the true value of the population parameter. This is associated with a degree of confidence, which is a measure the probability that a randomly selected confidence interval encloses the population parameter.

Confidence Level The confidence level is equal to 1 - , and is split between the two tails of the distribution Usually the confidence level is: 90% (meaning ) 95% (meaning ) OR 99% (meaning )

Confidence Intervals The Confidence Interval is expressed as: E is called the margin of error. For samples of size > 30,

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. If in addition you know the standard deviation for all accounts is $112, what can you say about the average balance of all VISA accounts? Build a 95% confidence interval.

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. If in addition you know the standard deviation for all accounts is $112, what can you say about the average balance of all VISA accounts? Build a 95% confidence interval.

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. If in addition you know the standard deviation for all accounts is $112, what can you say about the average balance of all VISA accounts? Build a 90% confidence interval.

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. If in addition you know the standard deviation for all accounts is $112, what can you say about the average balance of all VISA accounts? Build a 90% confidence interval.

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. If in addition you know the standard deviation for all accounts is $112, what can you say about the average balance of all VISA accounts? Build a 90% confidence interval.

Example Suppose you took a sample of 100 accounts from Visa and found the mean balance was $213. If in addition you know the standard deviation for all accounts is $112, what can you say about the average balance of all VISA accounts? Build a 90% confidence interval.
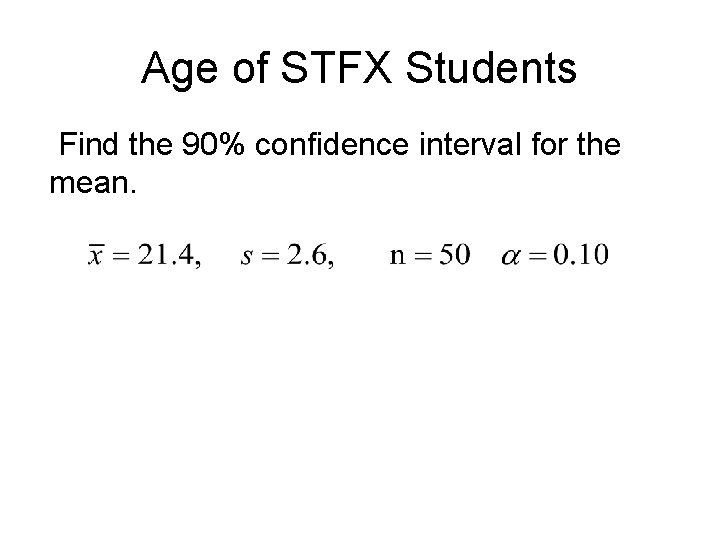
Age of STFX Students Find the 90% confidence interval for the mean.
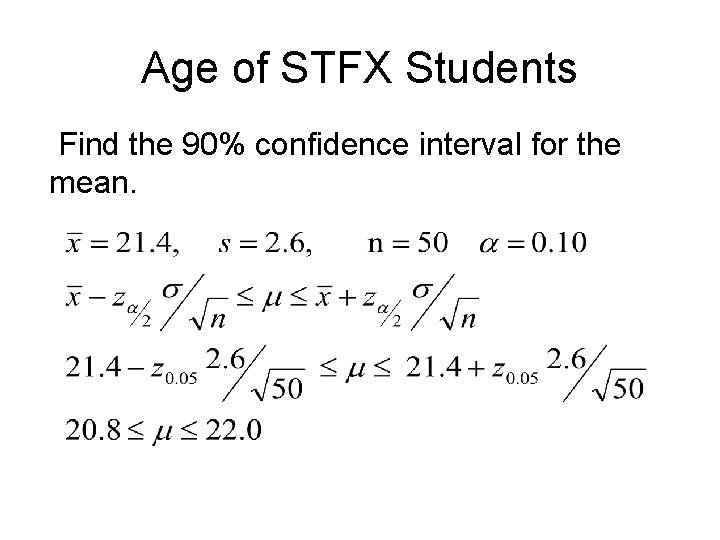
Age of STFX Students Find the 90% confidence interval for the mean.

Sample Size The sample size needed to estimate so as to be (1 -a)*100 % confident that the sample mean does not differ from more than E is: …round up

Overview • Confidence Intervals

Practice Problems • #7. 11 page 329 • #7. 19 page 331 • #7. 21 page 331

Homework • Review Chapter 7. 1, 7. 2 • Read Chapters 7. 3 -7. 5 26
- Slides: 26