Review David Kauchak cs 161 Summer 2009 Administrative

Review David Kauchak cs 161 Summer 2009

Administrative l l $ hw 6 solution out soon Remote final Check grades on coursework

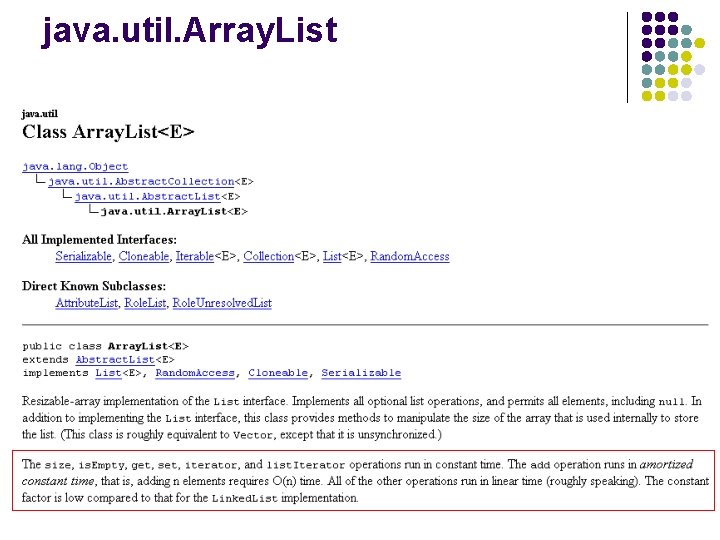
java. util. Array. List l l Extensible array implementation, i. e supports any arbitrary number of “add” operations Supports: l l Set. Index(k, x) – set element at index k to x Get. Index(k) – get the element at index k Add(x) – append the element to the end of the array They claim constant time for all these operations

Implementation? l Build on top of a basic array Initially, array is of a fixed size, say n l When an “add” happens l l l If number of elements < n l just add the new element If number of elements = n l Create a new array of size 2 n l Copy the initial n elements over l add the new element

Run time l Set. Index(k, x) l l Get. Index(k) l l O(1) Add(x) l O(n) – worst case we have to create a new array and copy all n elements over

Amortized analysis l l The time required to perform a sequence of operations is average over all of the operations performed What is the overall cost of n+1 Add operations? l l l n+1 adds n copies 2 n allocating memory (depending on the implementation) 4 n+1 operations Amortized cost of n+1 adds? l 4 n+1/n+1 = O(1)

java. util. Array. List

Sorting l Algorithms l l l Mergesort Insertion sort Selection sort Bubblesort Quicksort (randomized quicksort) Heapsort

Sorting l Algorithm features (in place, stable) Runtime Randomized quicksort analysis How they operate Decision tree model Lower bound on comparison based sorting l Divide and conquer l l l

Big O l l l O, Θ, Ω Proving bounds don’t hold Estimating bounds from real world data Comparing/ranking functions l rules of thumb

Recurrences l Solving recurrences l l recursion-tree method substitution method master method Defining recurrences from algorithms

Search trees l Trees l l Definitions Tree types/characteristics l l l l Binary search trees (BSTs) B-trees balanced full complete … What are they good for Operations Runtime

Data structures l Basic l l l l Binary heaps (i. e. priority queues) Definitions/characteristics what they’re good for operations/how they operate l linked lists stacks queues heapify building a heap runtime

Hashtables l l l Hash functions, what makes a valid hash function Collision by chaining Open addressing l l l l linear probing quadratic probing double hashing What they’re good for operations how they operate collision analysis runtime

Graphs l Types of graphs l l l l l directed undirected weighted trees dags complete bipartite cyclic connected

Graphs l Representation l l adjacency list adjacency matrix benefits/drawbacks Algorithms l l l BFS DFS Topological sort

Graphs l Algorithms l Single source shortest paths l l l Minimum spanning tress (MSTs) l l l l Dijkstra’s – positive weights Bellman-Ford – general graphs minimum cut property Kruskal’s algorithm Prim’s algorithm how they operate when to apply runtimes Developing new algorithms Runtime analysis (in terms of both |V| and |E|)

Greedy algorithms l l l What makes for a greedy problem/solution? Identifying greedy problems proving greedy problems are optimal l l “stays ahead” argument Examples l l Interval scheduling horn formulas Fractional knapsack problem Huffman coding algorithms

Dynamic programming l l l Identifying and solving dynamic programming problems Defining recursive definition Identifying repeated problems Bottom-up approach Examples l l l Fibonacci Counting binary search trees Longest commons subsequence Longest increasing subsequence Memoization Greedy vs. DP problems

String algorithms l l l Edit distance String operations String matching l l l Naïve approach FSA l building an FSA from a pattern l FSA operations Rabin-Karp algorithm How they operate Runtimes

LPs l l l Definition of an LP Normal form Graphical representation of constraints Creating LPs from word problems Solving LPs l l What makes a program solvable Simplex method l finding neighbors l determining if we’re at the max l runtime analysis

Problem solving techniques l l l Divide and conquer Dynamic programming Greedy

Material covered l l l Slides - >1300 Notes pages - 97 Comments – 458 posts on the discussion board

How far have we come… l l l Describe the algorithm for a depth first search traversal Write a function f(a, b) which takes two character string arguments and returns a string containing only the characters found in both strings in the order of a. Write a version which is order N-squared and one which is order N. You're given an array containing both positive and negative integers and required to find the sub-array with the largest sum in O(n) time. Write a routine in C for the above. Reverse a linked list Insert in a sorted linked list Write a function to find the depth of a binary tree

General exam taking practices l T/F l l l l require an explanation! Read the questions carefully! Make sure you answer everything the question asked Read over all of the questions Solve the easy ones first Don’t spend too much time on any given problem Think about how you might be able to reuse an existing algorithm/approach

Contact info l [first_name_initial][last_name]@gmail. com