Review Confidence Intervals Sample Size Estimator and Point

Review • Confidence Intervals • Sample Size

Estimator and Point Estimate An estimator is a “sample statistic” (such as the sample mean, or sample standard deviation) used to approximate a population parameter. A Point Estimate is a single value or point used to approximate a population parameter. A point estimator may be biased or unbiased.

Central Limit Theorem Take ANY random variable X and compute m and s for this variable. If samples of size n are randomly selected from the population, then: 1) For large n, the distribution of the sample means, will be approximately a normal distribution, 2) The mean of the sample means will be the population mean m and 3) The standard deviation of the sample means will be

Confidence Intervals The Confidence Interval is expressed as: E is called the margin of error. For samples of size > 30,

Sample Size The sample size needed to estimate m so as to be (1 -a)*100 % confident that the sample mean does not differ from m more than E is: …round up

Practice Problems • #7. 11 page 329 • #7. 19 page 331 • #7. 21 page 331

Small Samples What happens if and n is small (n < 30)? Our formulas from the last section no longer apply.

Small Samples What happens if and n is small (n < 30)? Our formulas from the last section no longer apply. There are two main issues that arise for small samples: 1) s no longer can be approximated by s 2) The CLT no longer holds. That is the distribution of the sampling means is not necessarily normal.

t- distribution If we have a small sample (n < 30) and wish to construct a confidence interval for the mean we can use a t-statistic, provided the sample is drawn from a normally distributed population.

t-distributions s is unknown so we use s (the sample standard deviation) as a point estimate of s. We convert the nonstandard t-distributed problem to a standard t-distributed problem through the use of the standard t-score

t-distributions • Mean 0 • Symmetric and bell-shaped • Shape depends upon the degrees of freedom, which is one less than the sample size. df = n-1 • Lower in center, higher tails than normal. • See Table inside front cover in text

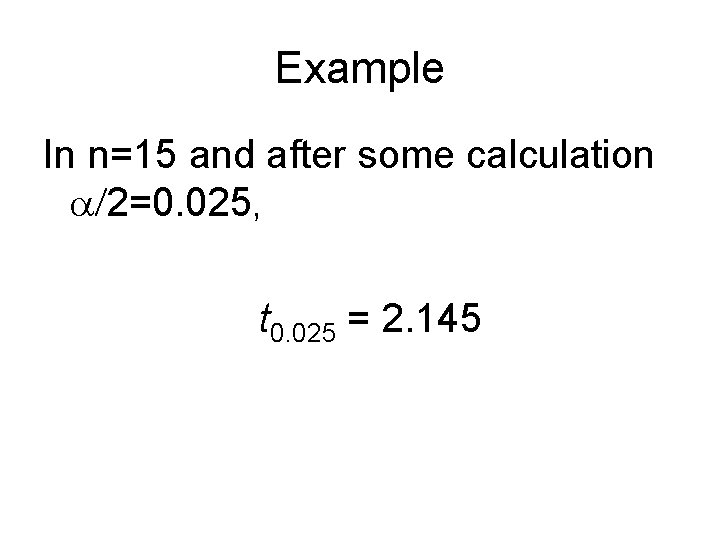
Example In n=15 and after some calculation a/2=0. 025, t 0. 025 = 2. 145

Confidence Interval for the mean when s is unknown and n is small The (1 - a)*100% confidence interval for the population mean m is The margin of error E, is in this case N. B. The sample is assumed to be drawn from a normal population.

Confidence Intervals for a small sample population mean The Confidence Interval is expressed as: The degrees of freedom is n-1.

Example The following are the heat producing capabilities of coal from a particular mine (in millions of calories per ton) 8, 500 8, 330 8, 480 7, 960 8, 030 Construct a 99% confidence interval for the true mean heat capacity. Solution: sample mean is 8260. 0 sample Std. Dev. is 251. 9 degrees of freedom = 4 a = 0. 01 7741. 4 m 8778. 6

Confidence intervals for a population proportion The objective of many surveys is to determine the proportion, p, of the population that possess a particular attribute. If the size of the population is N, and X people have this attribute, then as we already know, is the population proportion.

Confidence intervals for a population proportion If the size of the population is N, and X people have this attribute, then as we already know, is the population proportion. The idea here is to take a sample of size n, and count how many items in the sample have this attribute, call it x. Calculate the sample proportion, . We would like to use the sample proportion as an estimate for the population proportion.

Therefore at the (1 -a)*100 % level of confidence, the Error estimate of the population proportion is At the (1 -a)*100 % level of confidence, the confidence interval for the population proportion is :

Determining Sample Size In calculating the confidence interval for the population proportion we used Perhaps we might be interested in knowing how large a sample we should use if we are willing to accept a margin of error E with a degree of confidence of 1 -a.

Determining Sample Size If we already have an idea of the proportion (either through a pilot study, or previous results) one can use If we have no idea of what the proportion is then we use

In Class Exercises • #7. 31, 7. 36, 7. 41 Pages 341, 342 • #7. 50, 7. 57 on page 349, 350 • #7. 75, 7. 78 Pages 356, 357

Shortcut for finding za/2 • Recall that as n the Student’s Tdistribution approaches the normal distribution. • Look at T-table inside front cover, the last row represents the values of tn-1, a/2, as n becomes large which is essentially za/2. • Therefore, for some common values of a we are able to find za/2 quite quickly. • z 0. 025 =1. 960, z 0. 10 =1. 282

Homework • Review Chapter 7. 3 -7. 5 • Read Chapters 8. 1 -8. 3 • Quiz on Tuesday: Chapter 5 23