REVIEW CHI SQUARED TEST Gene Linkage For unlinked

REVIEW: CHI - SQUARED TEST

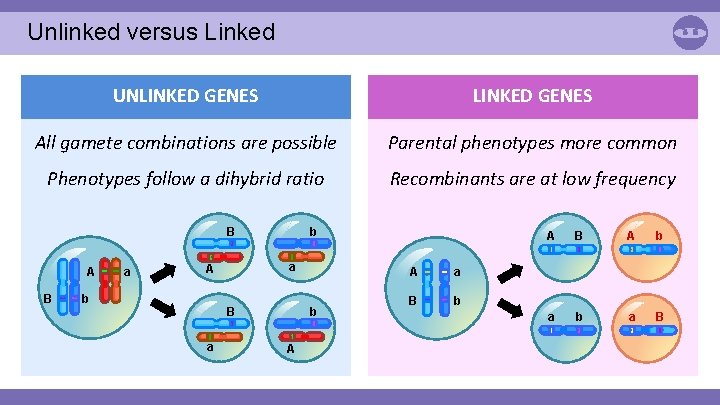
Gene Linkage For unlinked genes, any combination of traits can potentially occur in offspring • This is due to the independent assortment of chromosomes during meiosis For linked genes, only parental phenotypes commonly occur in the offspring • Recombinant phenotypes can occur, but only when crossing over occurs Hence, phenotypic ratios of offspring can be used to determine if genes are linked • Unlinked genes demonstrate expected ratios according to dihybrid patterns • Linked genes have very low frequencies of the recombinant phenotypes

Unlinked versus Linked UNLINKED GENES All gamete combinations are possible Parental phenotypes more common Phenotypes follow a dihybrid ratio Recombinants are at low frequency b B A B a a A b b B a A A a B b A B A b a B

Chi-Squared Test A chi-squared test can be used to determine if there is a statistically significant difference between the observed and expected frequencies of phenotypes A chi-squared test is completed via the following steps: • Identify a hypothesis (null hypothesis versus alternative hypothesis) • Construct a table of frequencies (observed versus expected data) • Apply the chi-squared formula to test for differences in the phenotypic ratios • Determine the degree of freedom and identify the p value (should be p<0. 05) Chi-squared tests determine whether differences in observed and expected frequency are significant

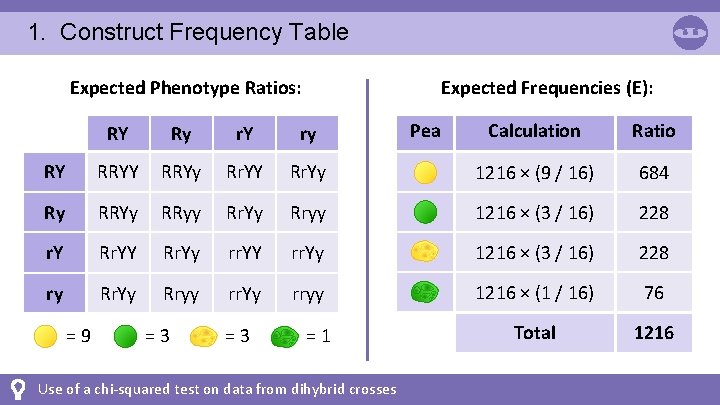
Chi-Squared Test: Worked Example A cross between two heterozygous pea plants was performed (Rr. Yy × Rr. Yy): • R = smooth • r = wrinkled • Y = yellow • y = green Smooth Yellow Smooth Green Wrinkled Yellow Wrinkled Green Total 701 peas 204 peas 243 peas 68 peas 1216 Two distinct hypotheses were formulated: • Null Hypothesis: There is no difference between frequencies (genes unlinked) • Alternative Hypothesis: There is a difference in the frequencies (genes linked) Use of a chi-squared test on data from dihybrid crosses

1. Construct Frequency Table Expected Phenotype Ratios: Expected Frequencies (E): Calculation Ratio Rr. Yy 1216 × (9 / 16) 684 Rr. Yy Rryy 1216 × (3 / 16) 228 Rr. Yy rr. YY rr. Yy 1216 × (3 / 16) 228 Rryy rr. Yy rryy 1216 × (1 / 16) 76 Total 1216 RY Ry r. Y ry RY RRYy Rr. YY Ry RRYy RRyy r. Y Rr. YY ry Rr. Yy =9 =3 =3 =1 Use of a chi-squared test on data from dihybrid crosses Pea

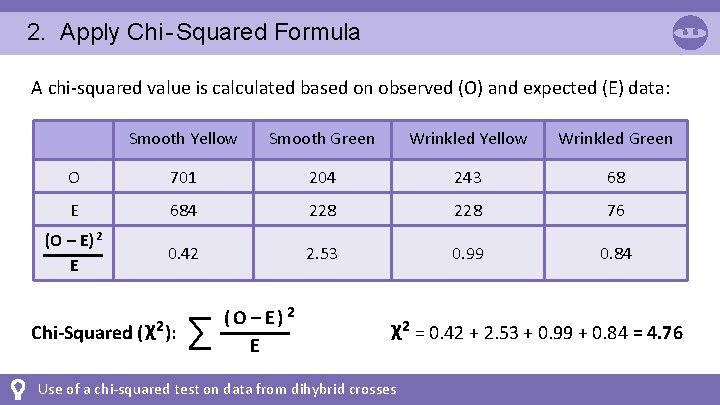
2. Apply Chi - Squared Formula A chi-squared value is calculated based on observed (O) and expected (E) data: Smooth Yellow Smooth Green Wrinkled Yellow Wrinkled Green O 701 204 243 68 E 684 228 76 (O – E) 2 E 0. 42 2. 53 0. 99 0. 84 Chi-Squared ( χ2 ): ∑ (O – E) 2 E χ2 = 0. 42 + 2. 53 + 0. 99 + 0. 84 = 4. 76 Use of a chi-squared test on data from dihybrid crosses

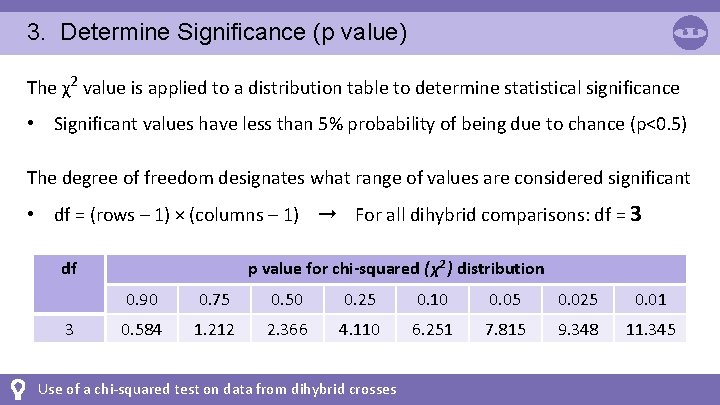
3. Determine Significance (p value) The χ2 value is applied to a distribution table to determine statistical significance • Significant values have less than 5% probability of being due to chance (p<0. 5) The degree of freedom designates what range of values are considered significant • df = (rows – 1) × (columns – 1) ➞ For all dihybrid comparisons: df = 3 p value for chi-squared ( χ2 ) distribution df 3 0. 90 0. 75 0. 50 0. 25 0. 10 0. 05 0. 025 0. 01 0. 584 1. 212 2. 366 4. 110 6. 251 7. 815 9. 348 11. 345 Use of a chi-squared test on data from dihybrid crosses

4. Draw Conclusions Based on the data collected, the distribution pattern is not statistically significant • The chi-squared (χ2) value calculated from the collected data was 4. 76 • This value lies below the minimum threshold for significance (p<0. 5 = 7. 815) As the results are not statistically significant, the alternative hypothesis is rejected • Null hypothesis: There is not a statistically significant difference detected between the observed (O) and the expected (E) frequencies • This means it can be concluded that there is no linkage (i. e. genes = unlinked) Use of a chi-squared test on data from dihybrid crosses

Topic Review Steps Involved in Chi-Squared Test: • Select traits of interest for analysis • Identify hypotheses (null vs alternative) • Collect data (phenotype numbers) • Calculate expected frequencies • Apply the chi-squared formula • Determine significance (p<0. 05) • Draw appropriate conclusions