REVIEW A matrix equation has the same solution

REVIEW A matrix equation has the same solution set as the vector equation which has the same solution set as the linear system whose augmented matrix is Therefore: Ax = b has a solution if and only if b is a linear combination of columns of A

REVIEW Theorem 4: The following statements are equivalent: 1. For each vector b, the equation has a solution. 2. Each vector b is a linear combination of the columns of A. 3. The columns of A span 4. A has a pivot position in every row. 1. Note: Theorem 4 is about a coefficient matrix A, not an augmented matrix.

1. 5 Solution Sets of Linear Systems

Definition of Homogeneous A system of linear equations is said to be homogeneous if it can be written in the form Ax = 0, where A is an matrix and 0 is the zero vector in Rm. Example: Note: Every homogeneous linear system is consistent. i. e. The homogeneous system Ax = 0 has at least one solution, namely the trivial solution, x = 0.

Important Question When does a homogenous system have a non-trivial solution? That is, when is there a non-zero vector x such that ?

Example 1: Determine if the following homogeneous system has a nontrivial solution: Geometrically, what does the solution set represent?

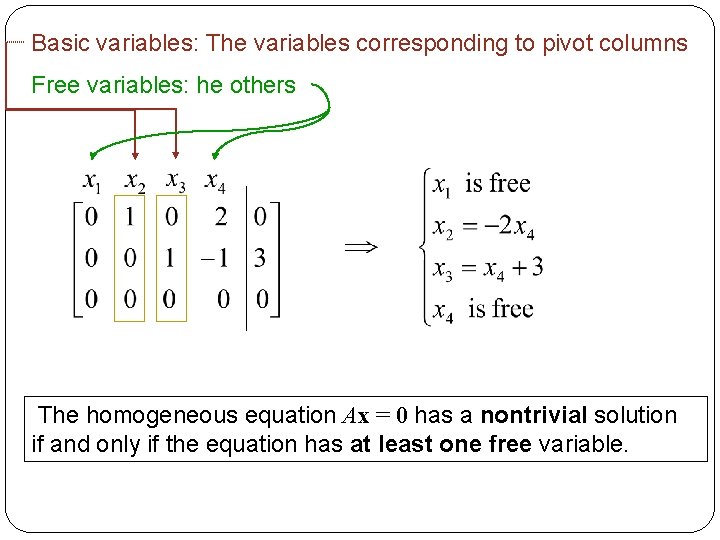
Basic variables: The variables corresponding to pivot columns Free variables: he others The homogeneous equation Ax = 0 has a nontrivial solution if and only if the equation has at least one free variable.

Example 2: Describe all solutions of the homogeneous system Geometrically, what does the solution set represent?

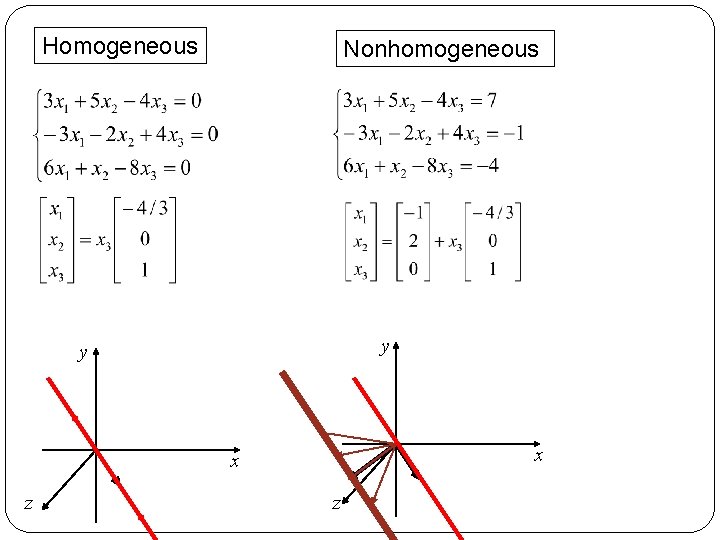
Solutions of Nonhomogeneous Systems Example 3: Describe all solutions for i. e. Describe all solutions of where and Geometrically, what does the solution set represent?

Homogeneous Nonhomogeneous

Homogeneous Nonhomogeneous y y x x z z

Theorem 6 Suppose is consistent for some given b, and let p be a solution. Then the solution set of is the set of all vectors of the form where is any solution of the homogeneous equation.