Review 3 D Transforms Continued Rotation about an

Review: 3 D Transforms Continued Rotation about an arbitrary axis Quaternions

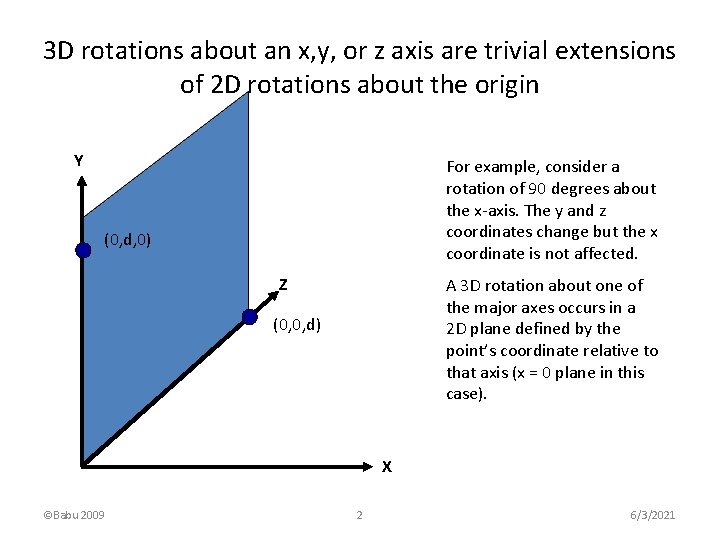
3 D rotations about an x, y, or z axis are trivial extensions of 2 D rotations about the origin Y For example, consider a rotation of 90 degrees about the x-axis. The y and z coordinates change but the x coordinate is not affected. (0, d, 0) Z A 3 D rotation about one of the major axes occurs in a 2 D plane defined by the point’s coordinate relative to that axis (x = 0 plane in this case). (0, 0, d) X ©Babu 2009 2 6/3/2021

3 D Rotation about the x axis By looking at the 2 D rotation matrix we can write down what the 3 D rotation matrix about the x axis must look like: 6/3/2021 ©Babu 2009 3

Translations are defined relative to the x, y, and z axes • Notation: P’ = Tx(5)P • Implementation • Meaning: Move the position of point P five units in a positive direction with respect to the x axis – New point is (x+5, y, z) ©Babu 2009 4 6/3/2021

Rotation about the x axis • Notation P’ = Rx(30)P • Implementation (Homogenous Coordinates) • Meaning – Rotate a point P a positive 30 degrees about the x-axis ©Babu 2009 5 6/3/2021

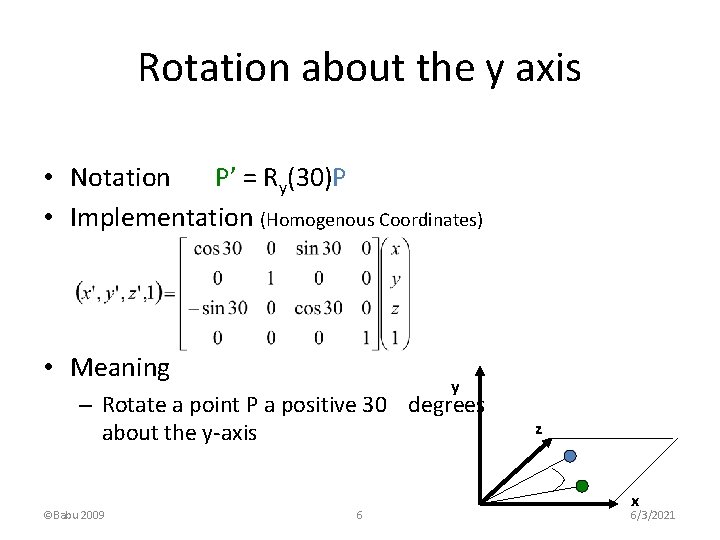
Rotation about the y axis • Notation P’ = Ry(30)P • Implementation (Homogenous Coordinates) • Meaning y – Rotate a point P a positive 30 degrees about the y-axis ©Babu 2009 6 z x 6/3/2021

Rotation about the z axis • Notation P’ = Rz(30)P • Implementation (Homogenous Coordinates) • Meaning – Rotate a point P a positive 30 degrees about the z-axis ©Babu 2009 7 6/3/2021

Rotation About An Arbitrary Axis p 2 u Z θ p 1 Y 6/3/2021 ©S. Babu X 8

Rotation About An Arbitrary Axis Translate p to origin 1 p 2 T(-p 1) u Z p 1 u' 6/3/2021 ©S. Babu Y X 9

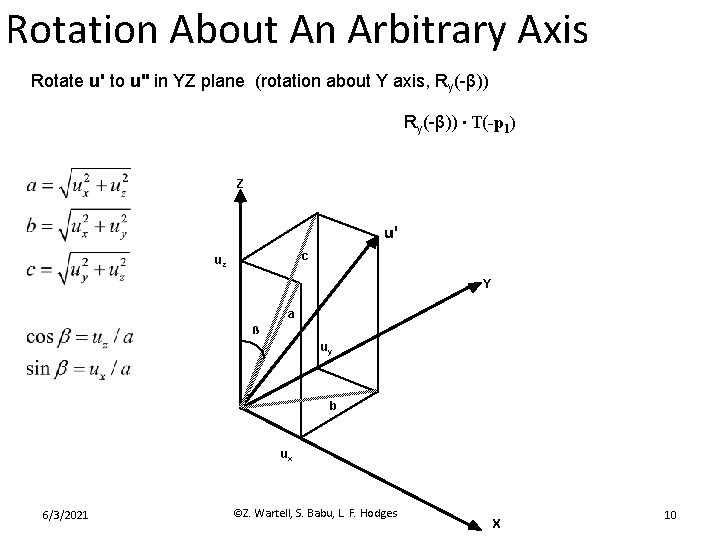
Rotation About An Arbitrary Axis Rotate u' to u'' in YZ plane (rotation about Y axis, Ry(-β)) ∙ T(-p 1) Z u' c uz Y a ß uy b ux 6/3/2021 ©Z. Wartell, S. Babu, L. F. Hodges X 10

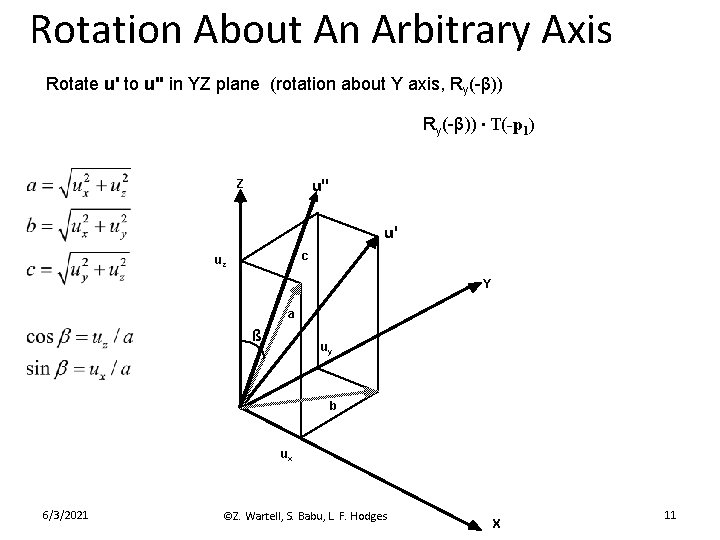
Rotation About An Arbitrary Axis Rotate u' to u'' in YZ plane (rotation about Y axis, Ry(-β)) ∙ T(-p 1) u'' Z u' c uz Y a ß uy b ux 6/3/2021 ©Z. Wartell, S. Babu, L. F. Hodges X 11

Rotation About An Arbitrary Axis After Ry(-ß), angle α and u'' lies in the y-z plane. Next, Rotate u'' to Z axis (u''') (rotation about X axis, Rx(α)) Rx(α) ∙ Ry(-β) ∙ T(-p 1) u'' Z a c uz Y α uy ux 6/3/2021 ©S. Babu X 12

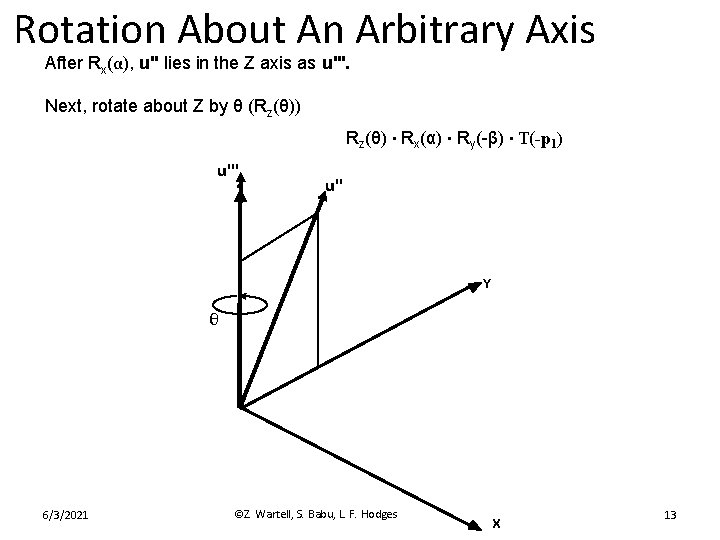
Rotation About An Arbitrary Axis After Rx(α), u'' lies in the Z axis as u'''. Next, rotate about Z by θ (Rz(θ)) Rz(θ) ∙ Rx(α) ∙ Ry(-β) ∙ T(-p 1) u''' Z u'' Y θ 6/3/2021 ©Z. Wartell, S. Babu, L. F. Hodges X 13

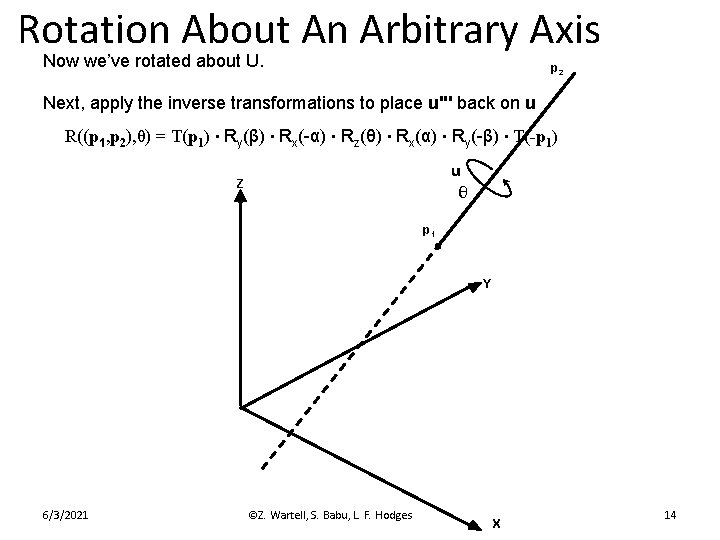
Rotation About An Arbitrary Axis Now we’ve rotated about U. p 2 Next, apply the inverse transformations to place u''' back on u R((p 1, p 2), θ) = T(p 1) ∙ Ry(β) ∙ Rx(-α) ∙ Rz(θ) ∙ Rx(α) ∙ Ry(-β) ∙ T(-p 1) u θ Z p 1 Y 6/3/2021 ©Z. Wartell, S. Babu, L. F. Hodges X 14

Rotation About An Arbitrary Axis 6/3/2021 ©Z. Wartell, S. Babu 15

Quaternions Alternative rotation representation: 4 real numbers interpolation between quaternions well defined (“slerp”) no gimbal lock composition of quaternions: 16 *’s, 9+’s (matrix 27 *’s and 18 +’s) 6/3/2021 ©Z. Wartell, S. Babu 16

Quaternions • Rotation representation: Relation to axis-angle representation (u, θ) is: y u θ

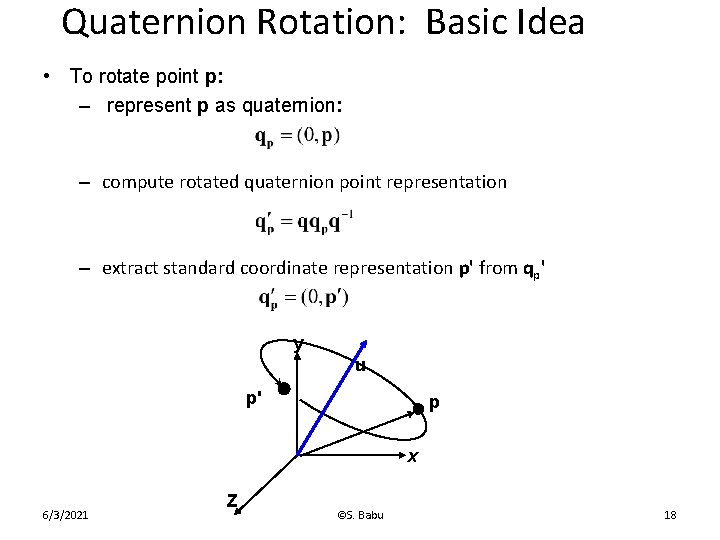
Quaternion Rotation: Basic Idea • To rotate point p: – represent p as quaternion: – compute rotated quaternion point representation – extract standard coordinate representation p' from qp' y u p' p x 6/3/2021 Z ©S. Babu 18

Details of Rotation • How do you multiply quaternions: • How do you find inverse of quaternion: • For rotations we assume unit quaternions, hence: 6/3/2021 ©S. Babu 19

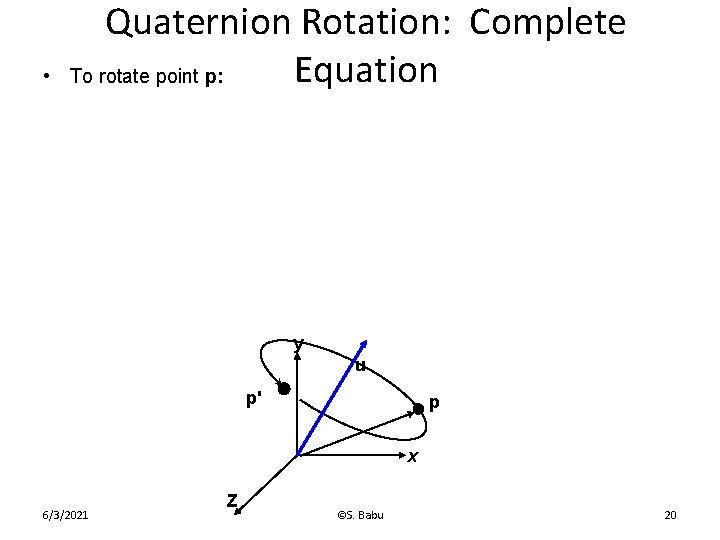
• Quaternion Rotation: Complete Equation To rotate point p: y u p' p

How do quaternions help? • Quaternion composition: requires 16 *’s, 12+’s while 3 x 3 matrix composition needs 27*’s and 18+’s • No gimbal lock • interpolation between two orientations using “spherical linear interpolation” (slerp) of their quaternions: -constant angular velocity -unique interpolation -interpolation that is same regardless of coordinate system used for computation 6/3/2021 ©Z. Wartell, S. Babu 21