Reversible and irreversible processes In the previos chapter

Reversible and irreversible processes

• In the previos chapter the energy equations for non flow and flow processes are derived. • The concept of reversibility and irreversibility are introduced and the properties of vapours and perfect gases are discussed. • It is the purpose of this chapter to consider processes in practice , and to combine with the work of previous chapter.

Reversible non flow processes Constant volume process • In a constant volume process the working substance is contained in a rigid vessel • hence the boundaries of the systems are immoveable • and no work can be done on or by the system. • It will be assumed that “constant volume “ implies zero work unless stated otherwise.

• From the non flow energy equation , for unit mass Q + w = u 2 – u 1 • Since no work is done, we therefore have Q= u 2 - u 1 • or for mass m, of the working substance Q= u 2 - u 1 • All the heat supplied in a constant volume process goes to increase the internal energy.

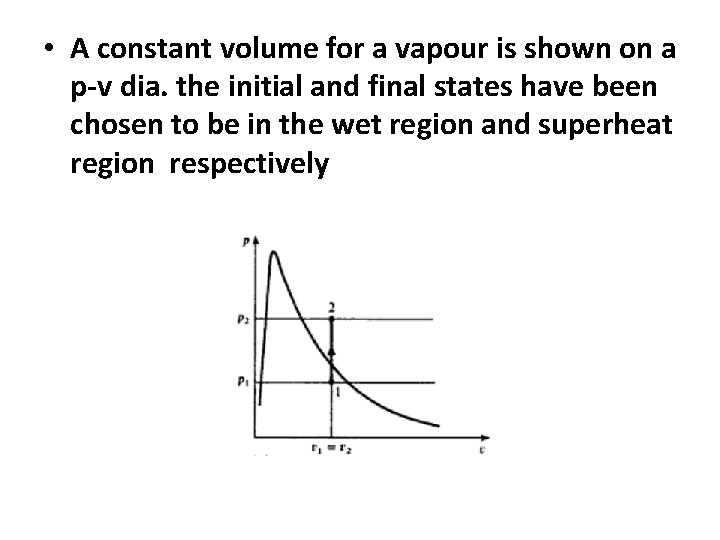
• A constant volume for a vapour is shown on a p-v dia. the initial and final states have been chosen to be in the wet region and superheat region respectively

• a constant volume process is shown on p- v diagram for a perfect gas. For a perfect gas we have from equation. • Q= mc (T 2 - T 1)

COSTANT PRESSURE PROCESS. • It can be seen from the figs in previous slides that when the boundary of the system is inflexible as in a constant volume process , then the pressure rises when heat is supplied • hence for a constant pressure, the boundry must move against an external resistance as heat is supplied. • For instance a fluid in a cylinder behind a piston can be made to undergo a constant pressure process. • Since the piston is pushed through a certain distance by the force exerted by the fluid, then the work is done by the fluid on the surroundings.

• From the equation of work done(first chapter) • Since p is constt • From the non flow equation Q + w = u 2 – u 1 hence for a reversible constant pressure process

• now from the equation enthalpy h=u + pv hence q= h 2 – h 1 • or for mass m, of a fluid. Q = H 2 - H 1

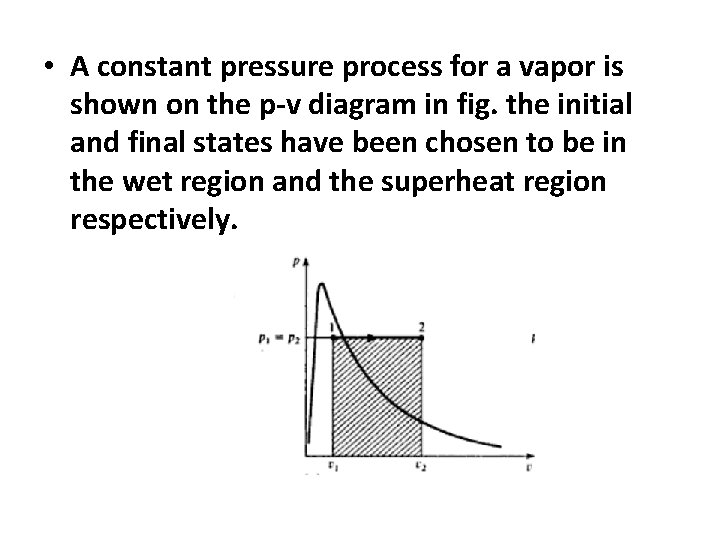
• A constant pressure process for a vapor is shown on the p-v diagram in fig. the initial and final states have been chosen to be in the wet region and the superheat region respectively.

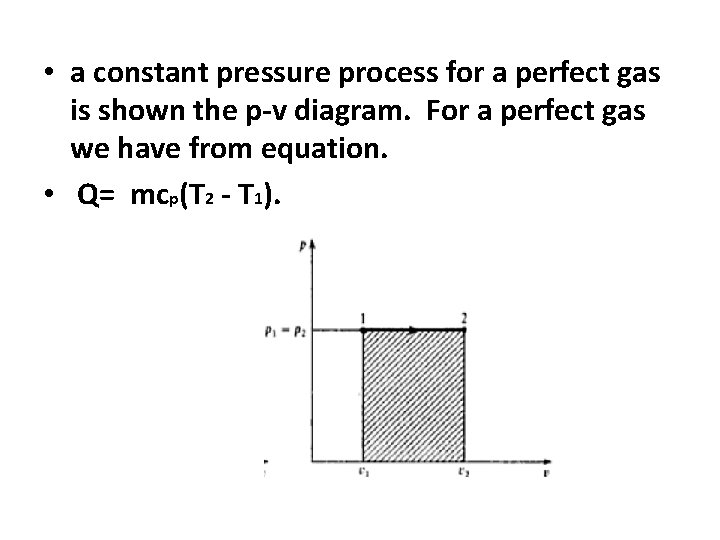
• a constant pressure process for a perfect gas is shown the p-v diagram. For a perfect gas we have from equation. • Q= mcp(T 2 - T 1).

Example • The mass of 0. 05 kg of a fluid is heated at a constant pressure of 2 bar until the volume occupied is 0. 0658 m 3, calculate the heat supplied and the work done I. When the fluid is steam initially dry saturated II. When the fluid is air, initially at 130 c

• Write data • And then possible diagram for the statement

CONSTANT TEMPERATURE OR ISOTHERMAL PROCESS • A process at constant temperature is called an isothermal process, • when a fluid in a cylinder behind a piston expends from a high pressure to a low pressure there is a tendency for the temperature to fall. • in an isothermal expansion heat must be added continuously an order to keep the temperature at the initial value, • similarly an isothermal compression heat must be removed from the fluid continuously during the process.

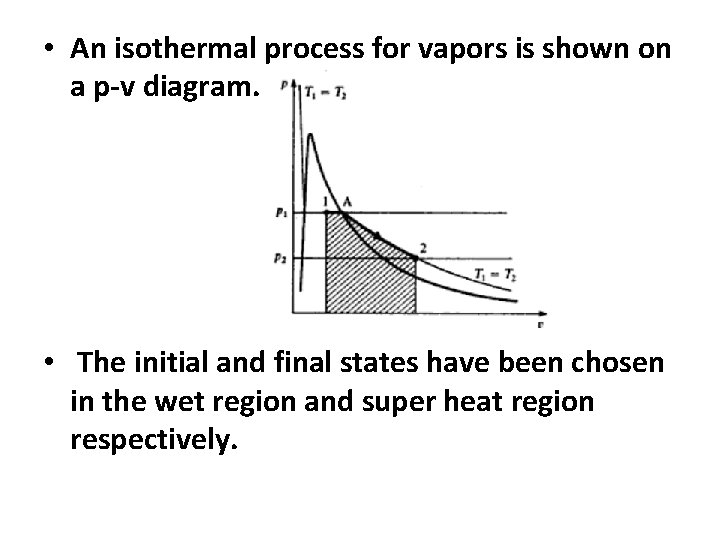
• An isothermal process for vapors is shown on a p-v diagram. • The initial and final states have been chosen in the wet region and super heat region respectively.

• From stat I to state A the pressure remains at P 1. since in the wet region the pressure and temperature are the corresponding saturation values. • it can be seen therefore that an isothermal process for wet steam is also at constant pressure. • And the super heat region the pressure falls to P 2 is shown in figures. And the procedure is not so simple.

• When state 1 and 2 are fixed than the internal energies U 1 and U 2 may be obtained from tables. • When the property and entropy (s), is introduced in chapter 4. convenient way of evaluating the heat supplied will be shown. • When the heat flow is calculated the work done can then be obtained using the nonflow energy equation. • for unit mass.

• An isothermal process for a perfect gas is more easily dealt with than an isothermal process for a vapor. since there are definite laws for a perfect gas. Relating P, v, T , and internal energy µ. we have , PV = RT • Now when the temperature is constant is an isothermal process than we have PV = RT constant • Therefore for an isothermal process for a perfect gas. PV = constant i-e. P 1 V 1 = P 2 V 2

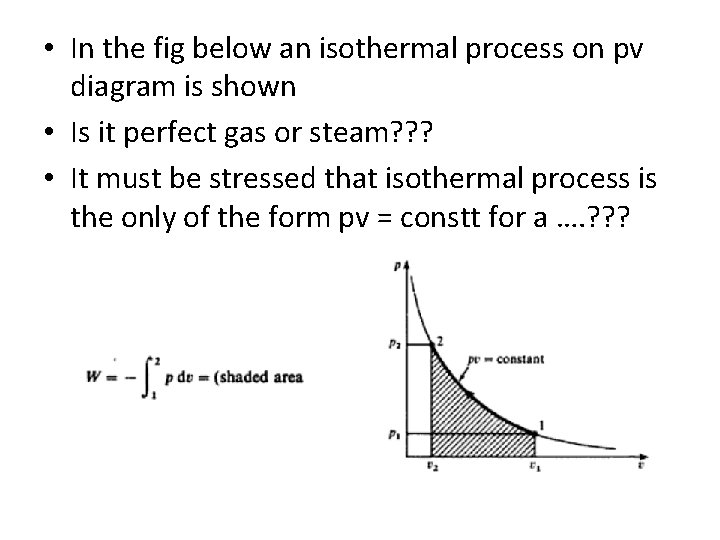
• In the fig below an isothermal process on pv diagram is shown • Is it perfect gas or steam? ? ? • It must be stressed that isothermal process is the only of the form pv = constt for a …. ? ? ?

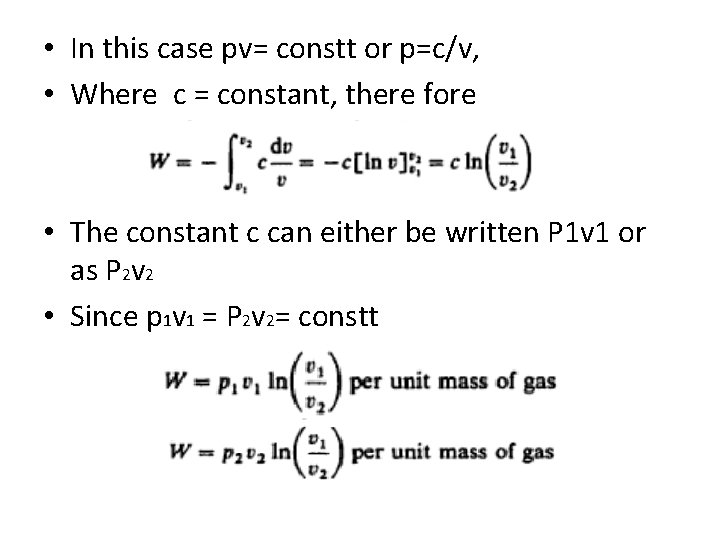
• In this case pv= constt or p=c/v, • Where c = constant, there fore • The constant c can either be written P 1 v 1 or as P 2 v 2 • Since p 1 v 1 = P 2 v 2= constt

continued • For a mass m of a gas W = p 1 V 1 ln(v 2/v 1) • Also since • Then p 1 v 1 = p 2 v 2 v 1/v 2 =p 2/p 1

• Substituting in the equation of work done W = p 1 v 1 ln(p 2/p 1) (per unit mass) • Or for mass m W = p 1 V 1 ln(p 2/p 1) Now p 1 v 1= RT Subsitute in the above equation what will be the form? ?

• Q+W = 0 • As internal energy is 0

numerical • 1 kg of nitrogen (molar mass 28 kg/kmol) is compressed reversibly and isothermally from 1. 01 bar, 20 C to 4. 2 bar. Calculate the work done and the heat flow during the process. Assume nitrogen to be perfect gas. • DATA • diagram