Reverse Hashing for Highspeed Network Monitoring Algorithms Evaluation

Reverse Hashing for High-speed Network Monitoring: Algorithms, Evaluation, and Applications Robert Schweller 1, Zhichun Li 1, Yan Chen 1, Yan Gao 1, Ashish Gupta 1, Yin Zhang 2, Peter Dinda 1, Ming-Yang Kao 1, Gokhan Memik 1 1 Lab for Internet and Security Technology (LIST), Northwestern Univ. 2 University of Texas at Austin

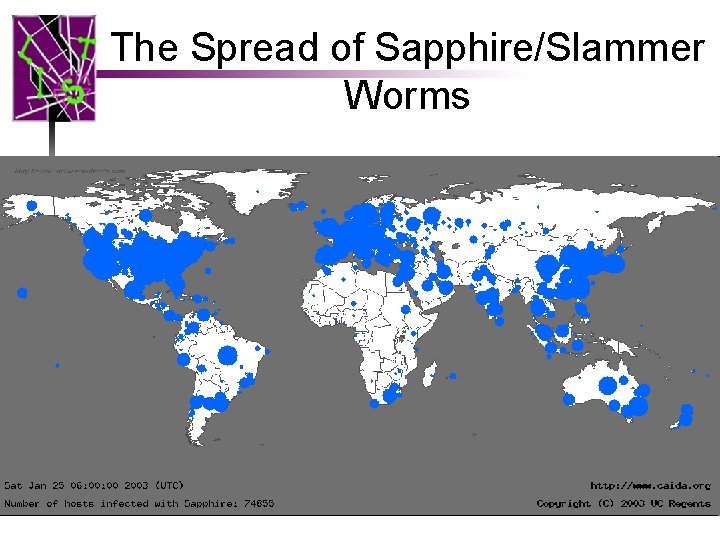
The Spread of Sapphire/Slammer Worms

Motivation (online change detection) • Online network anomaly/intrusion detection over high speed links – Small memory usage – Small # of memory access per packet – Scalable to large key space size • Primitives for online anomaly detection – Heavy hitters (lots of prior work) – Heavy changes: enabler for aggregate queries over multiple data streams • Asymmetric routing demands spatial aggregation • Time Series Analysis (TSA) need temporal aggregation

Outline • • Background on k-ary sketch Reversible sketch problem Modular hashing IP mangling Reverse hashing Evaluation Conclusion

K-ary sketch [Krishnamurthy, Sen, Zhang, Chen, 2003] First to detect flow-level heavy changes in massive data streams at network traffic speeds 0 1 1 … j … H … K-1

k-ary sketch [Krishnamurthy, Sen, Zhang, Chen, 2003] APIs: Update (k, u): Tj [ hj(k)] += u (for all j) 0 1 h 1(k) … K-1 1 … hj(k) j … h. H(k) H Estimate v(S, k): sum of updates for key k S=COMBINE(a, S 1, b, S 2): a +b =

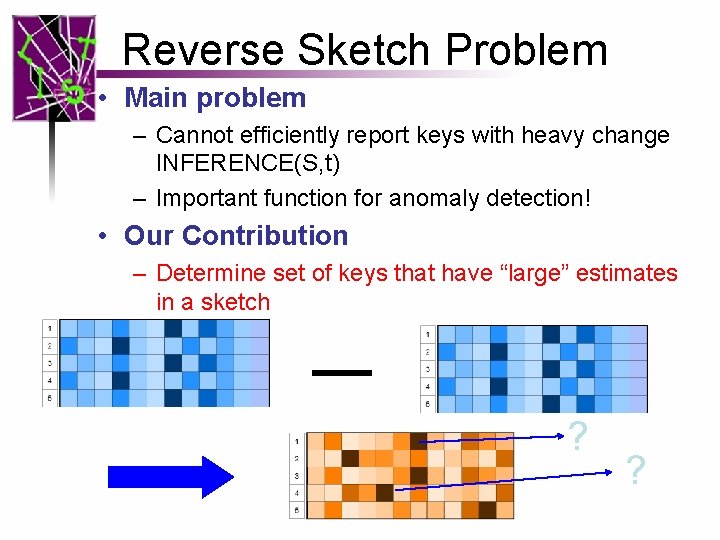
Reverse Sketch Problem • Main problem – Cannot efficiently report keys with heavy change INFERENCE(S, t) – Important function for anomaly detection! • Our Contribution – Determine set of keys that have “large” estimates in a sketch ? ?

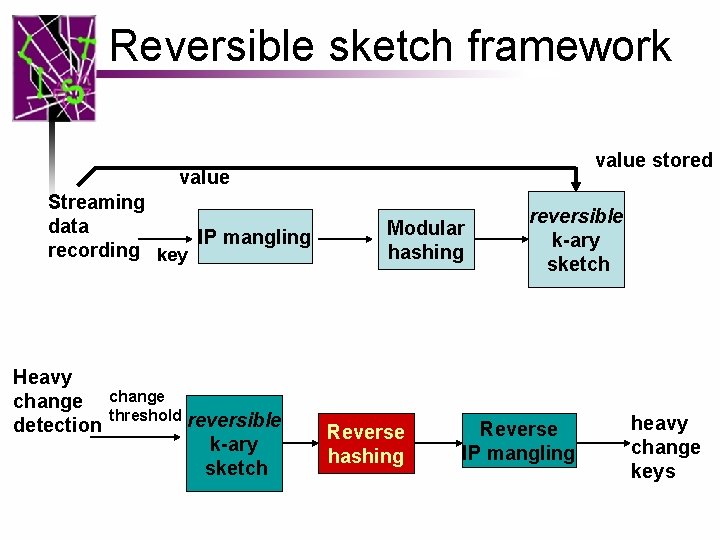
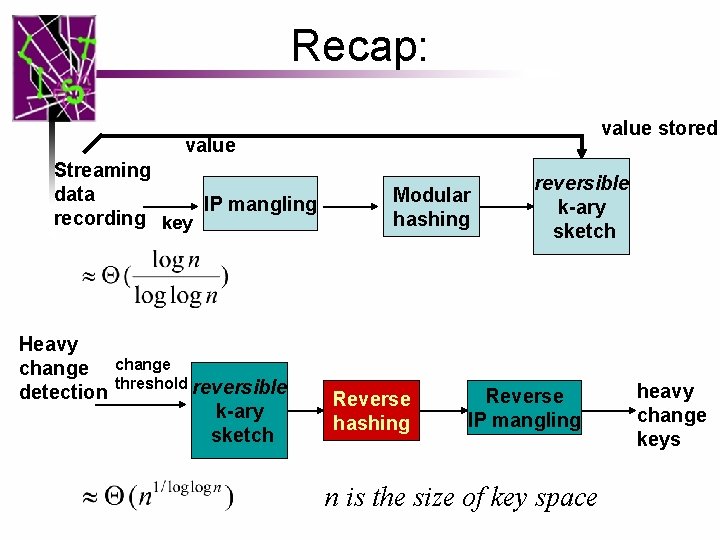
Reversible sketch framework value stored value Streaming data IP mangling recording key Heavy change detection change threshold reversible k-ary sketch Modular hashing Reverse hashing reversible k-ary sketch Reverse IP mangling heavy change keys

Outline • • Background on k-ary sketch Reversible sketch problem Modular hashing IP mangling Reverse hashing Evaluation Conclusion

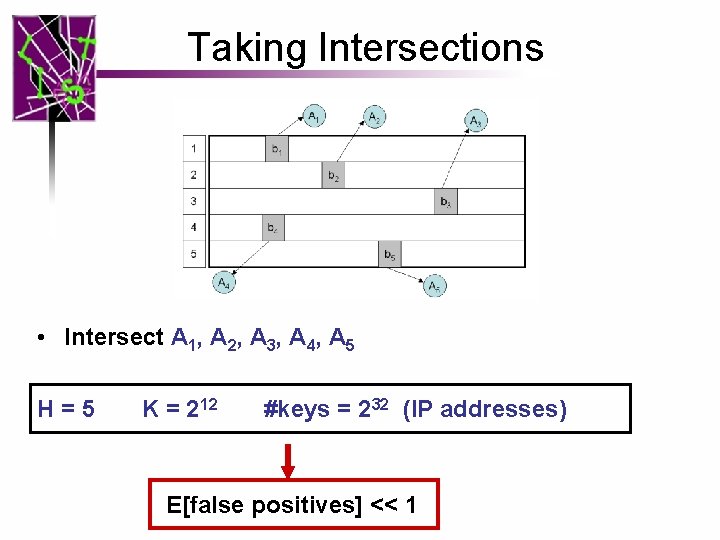
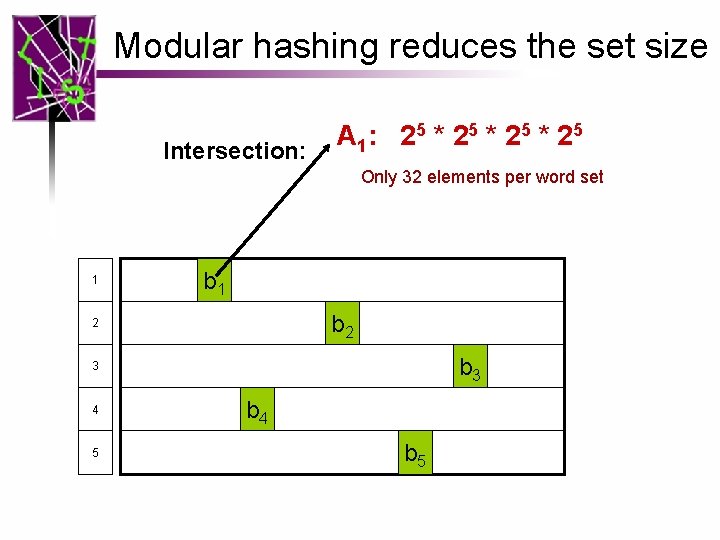
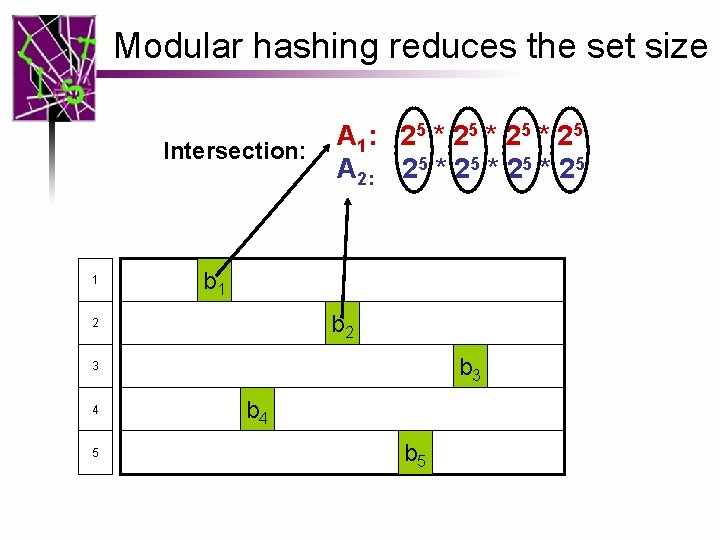
Taking Intersections • Intersect A 1, A 2, A 3, A 4, A 5 H=5 K = 212 #keys = 232 (IP addresses) E[false positives] << 1

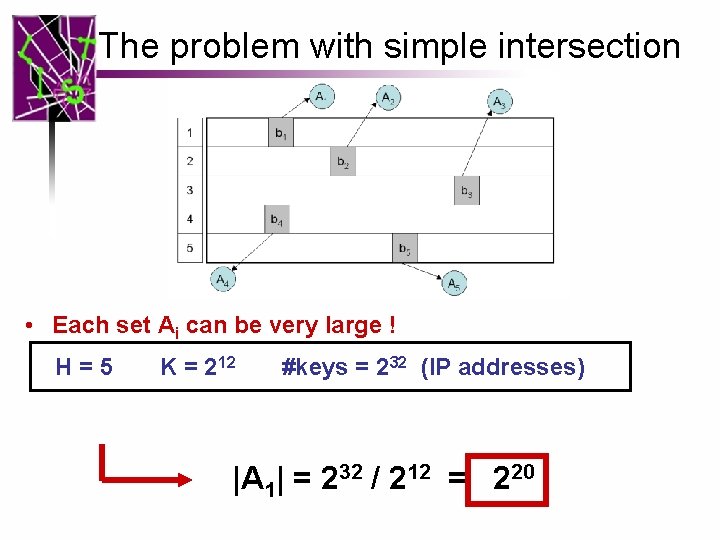
The problem with simple intersection • Each set Ai can be very large ! H=5 K = 212 #keys = 232 (IP addresses) |A 1| = 232 / 212 = 220

The problem with simple intersection • Each set Ai can be very large ! • Solution: Modular hashing

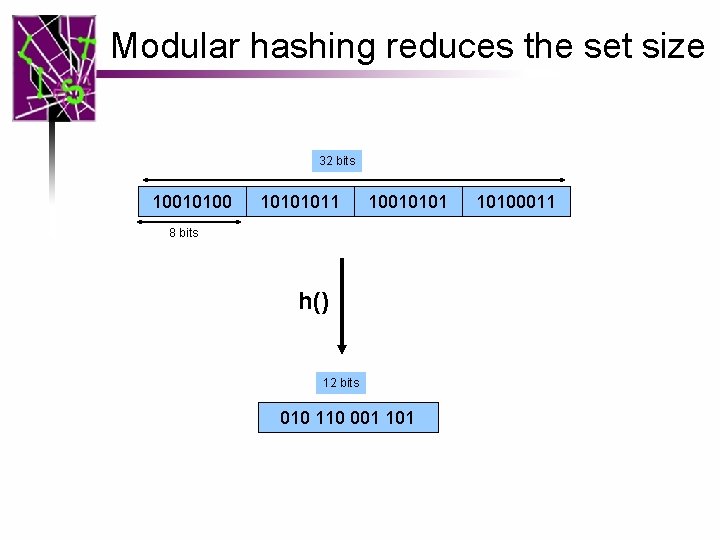
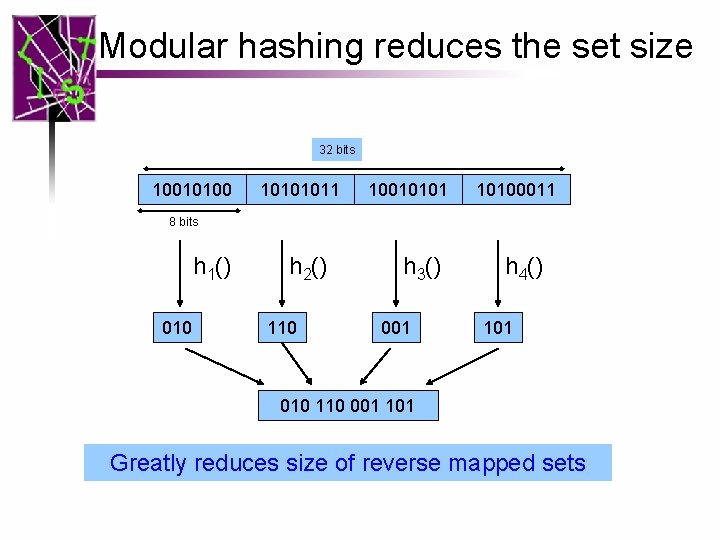
Modular hashing reduces the set size 32 bits 10010100 10101011 10010101 8 bits h() 12 bits 010 110 001 10100011

Modular hashing reduces the set size 32 bits 10010100 10101011 10010101 10100011 8 bits h 1() 010 h 2() 110 h 3() 001 h 4() 101 010 110 001 101 Greatly reduces size of reverse mapped sets

Modular hashing reduces the set size Intersection: A 1: 2 5 * 2 5 Only 32 elements per word set 1 b 2 2 b 3 3 4 5 b 4 b 5

Modular hashing reduces the set size Intersection: 1 A 1: 2 5 * 2 5 A 2: 25 * 25 b 1 b 2 2 b 3 3 4 5 b 4 b 5

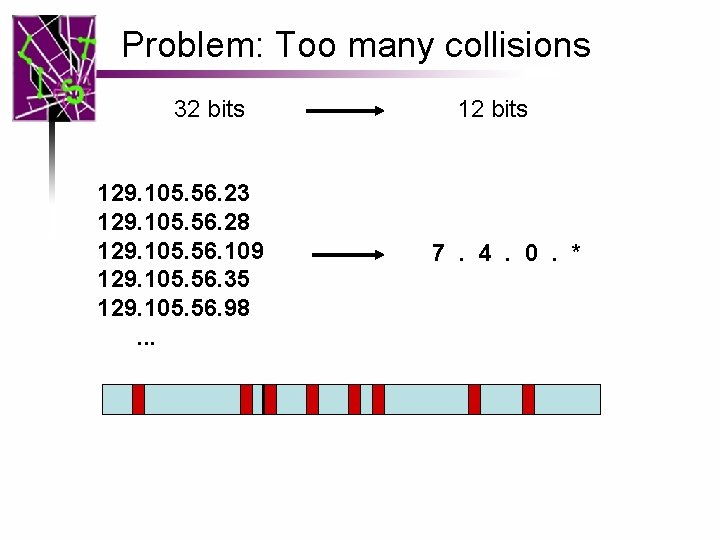
Problem: Too many collisions 32 bits 129. 105. 56. 23 129. 105. 56. 28 129. 105. 56. 109 129. 105. 56. 35 129. 105. 56. 98. . . 12 bits 7. 4. 0. *

Problem: Too many collisions 32 bits 129. 105. 56. 23 129. 105. 56. 28 129. 105. 56. 109 129. 105. 56. 35 129. 105. 56. 98. . . Solution: 12 bits 7. 4. 0. * IP Mangling with GF (Galois Extension Field) IP Mangling: a bijective mapping function for breaking the key space continuity

Outline • • Background on k-ary sketch Reversible sketch problem Modular hashing IP mangling Reverse hashing Evaluation Conclusion

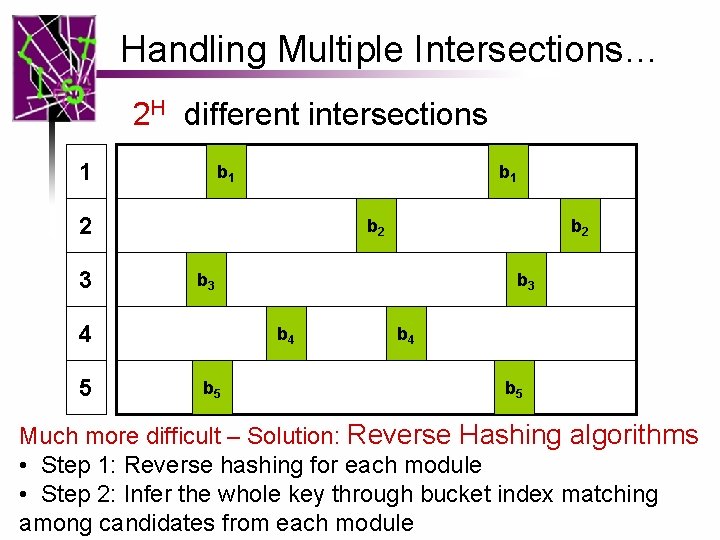
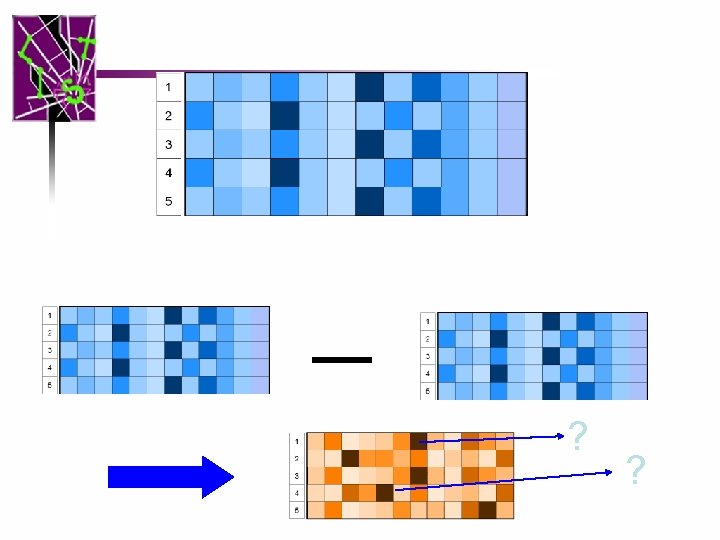
Handling Multiple Intersections… 2 H different intersections 1 b 1 2 3 b 2 b 3 4 5 b 2 b 3 b 4 b 5 Much more difficult – Solution: Reverse Hashing algorithms • Step 1: Reverse hashing for each module • Step 2: Infer the whole key through bucket index matching among candidates from each module

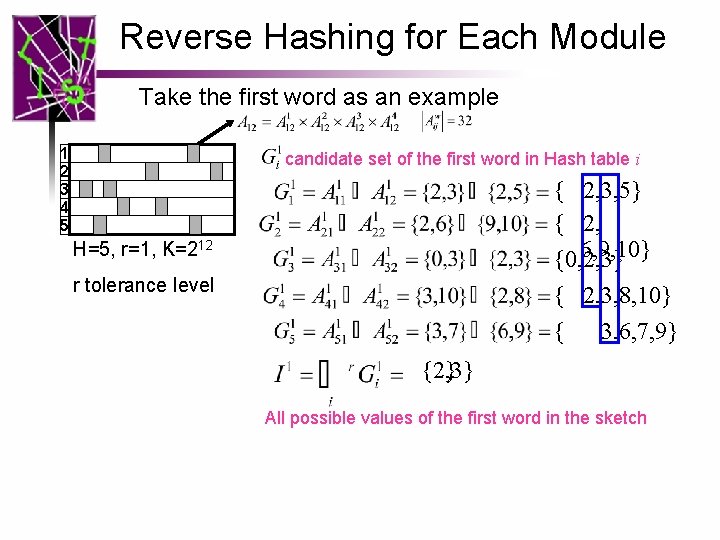
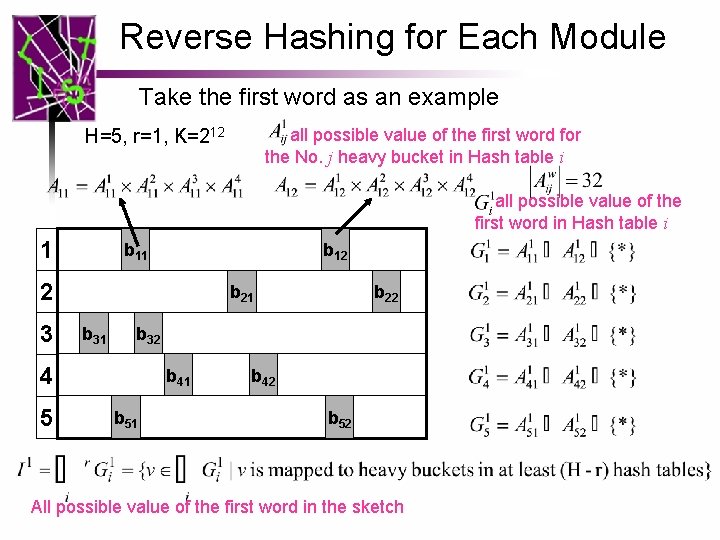
Reverse Hashing for Each Module Take the first word as an example 1 2 3 4 5 candidate set of the first word in Hash table i { 2, 3, 5} { 2, 6, 9, 10} {0, 2, 3} { 2, 3, 8, 10} { 3, 6, 7, 9} H=5, r=1, K=212 r tolerance level {2, 3} {2} All possible values of the first word in the sketch

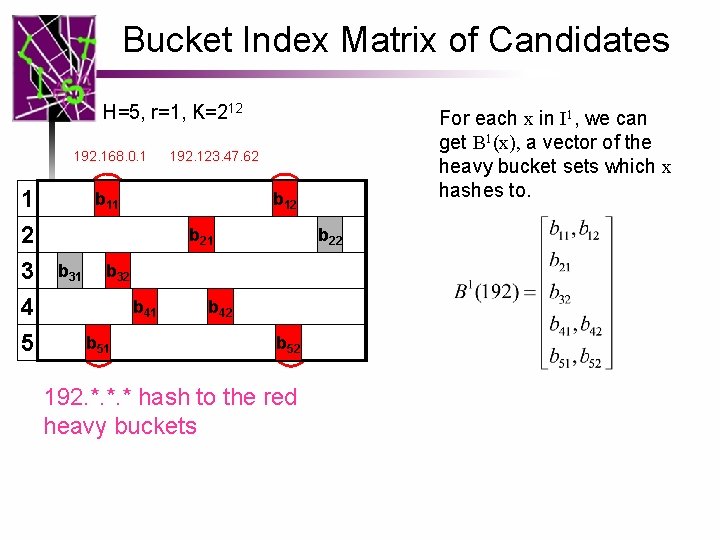
Bucket Index Matrix of Candidates H=5, r=1, K=212 192. 168. 0. 1 1 2 3 4 5 192. 123. 47. 62 b 11 b 12 b 21 b 31 b 22 b 32 b 41 b 51 For each x in I 1, we can get B 1(x), a vector of the heavy bucket sets which x hashes to. b 42 b 52 192. *. *. * hash to the red heavy buckets

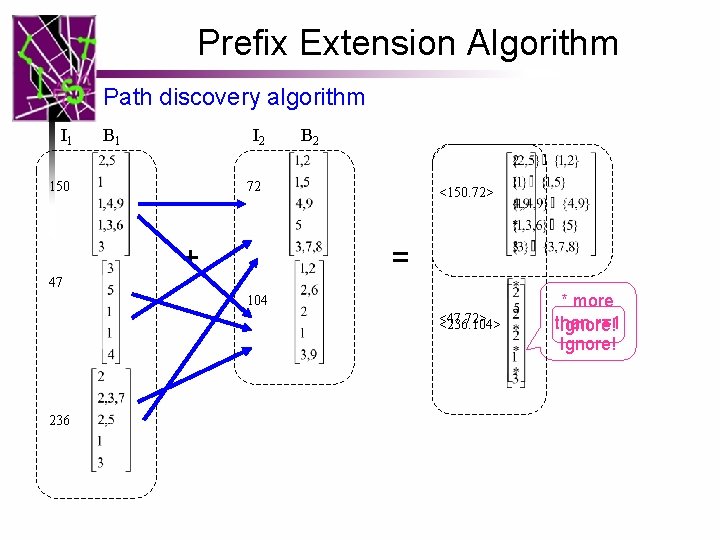
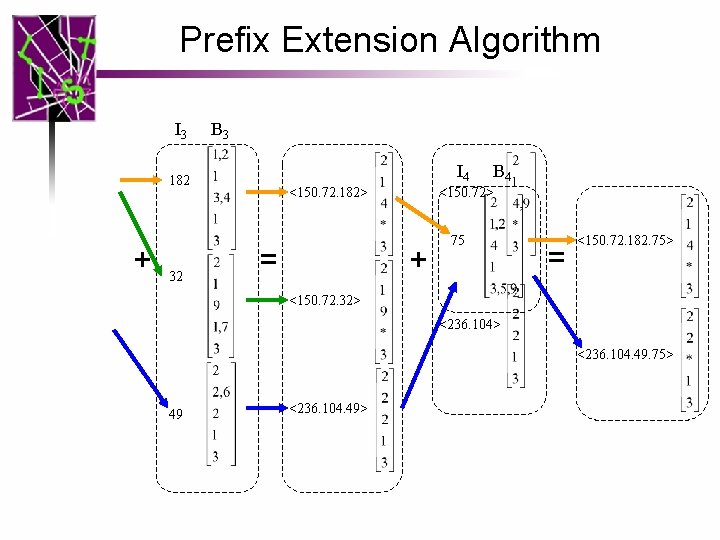
Prefix Extension Algorithm Path discovery algorithm I 1 B 1 I 2 150 47 B 2 72 + <150. 72> = 104 <47. 72> <236. 104> 236 * more than r=1 Ignore!

Prefix Extension Algorithm I 3 B 3 I 4 182 + 32 <150. 72. 182> = B 4 <150. 72> + 75 = <150. 72. 182. 75> <150. 72. 32> <236. 104. 49. 75> 49 <236. 104. 49>

Recap: value stored value Streaming data IP mangling recording key Heavy change detection change threshold reversible k-ary sketch Modular hashing Reverse hashing reversible k-ary sketch Reverse IP mangling n is the size of key space heavy change keys

Outline • • Background on k-ary sketch Reversible sketch problem Modular hashing IP mangling Reverse hashing Evaluation Conclusion

Evaluation • Dataset – A large US ISP (330 M Netflow records) – NU (19 M Netflow records) • Efficient data recording For the worst case traffic, all 40 -byte packets – – Software: 526 Mbps on P 4 3. 2 Ghz PC Hardware: 16 Gbps on a single FPGA broad Only a few hundred KB to a couple of MB memory used Only 15 memory access per packet for 48 bit reversible sketches and 16 per packet for 64 bit reversible sketches • Efficient heavy change detection and key inference – 0. 34 seconds for 100 changes. 13. 33 seconds for 1000 change

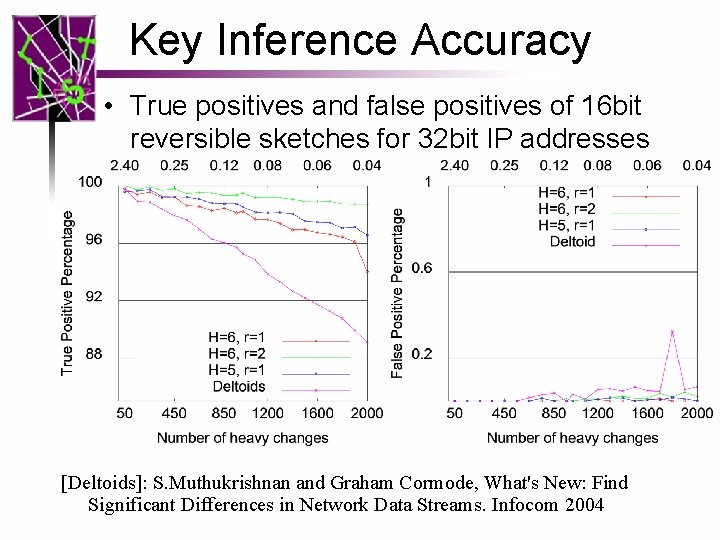
Key Inference Accuracy • True positives and false positives of 16 bit reversible sketches for 32 bit IP addresses [Deltoids]: S. Muthukrishnan and Graham Cormode, What's New: Find Significant Differences in Network Data Streams. Infocom 2004

More Results • Stress test with larger dataset still accurate • Scalable to larger key space size: similar results for 64 bit IP pairs • Built anomaly/intrusion detection system to detect, e. g. , SYN flooding and port scans [ICDCS 2006]

Conclusions Proposed the first reversible sketches which • Record high speed network streams online • Detect the heavy changes and infer the keys online • Small memory usage, small # of memory access per packet • Scalable to large key space size

Backup Slides

Related work • Compare with [deltoids] – Accuracy better – Scalable to large key space better – # of Memory access less • [PCF, IMC 2004]: not reversible • [Q. Zhao et al, IMC 2005] [S. Venkataraman, NDSS 2005]: unique fan -out (fan-in) estimation.

Modular Hashing Optimal Hashing

Reversible sketch problem However… Not reversible Lack of an inference API: INFERENCE(S, t) • Important function for anomaly detection! • Decouple the recording stage of sketches from the detection stage to enable efficient combine and inference. • Given a threshold t, report keys whose corresponding sum of updates are larger than the threshold. Our contribution: an efficient algorithm for inference

Problem: Too many collisions 32 bits 129. 105. 56. 23 129. 105. 56. 28 129. 105. 56. 109 129. 105. 56. 35 129. 105. 56. 98. . . 12 bits 7. 4. 0. * Solution: IP Mangling with

IP-mangling • Use GF (Galois Extension Field) function for attack resilience

Modular Hashing with IP Mangling Optimal Hashing

Reverse Hashing for Each Module Take the first word as an example all possible value of the first word for the No. j heavy bucket in Hash table i H=5, r=1, K=212 all possible value of the first word in Hash table i 1 b 12 2 3 b 21 b 32 4 5 b 22 b 41 b 51 b 42 b 52 All possible value of the first word in the sketch

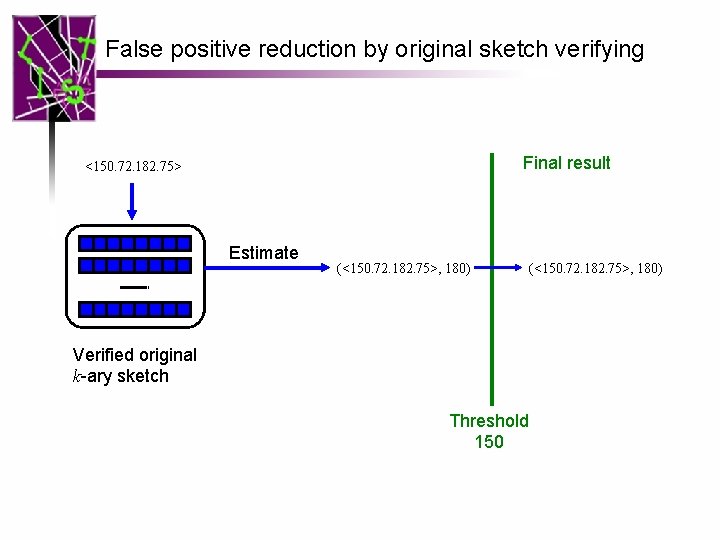
False positive reduction by original sketch verifying Final result <150. 72. 182. 75> Estimate (<150. 72. 182. 75>, 180) Verified original k-ary sketch Threshold 150 (<150. 72. 182. 75>, 180)

K-ary sketch [Krishnamurthy, Sen, Zhang, Chen, 2003] • first to detect flow-level heavy changes in massive data streams at network traffic speeds • APIs – UPDATE(S, k, u): Tj [ hj(k)] += u (for all j) – ESTIMATE(S, k): sum of updates for key k – Linear combination: S=COMBINE(a, S 1, b, S 2) a +b =