Reverse Factor Algorithm Speeding up on two string

Rule 1: The Suffix to Prefix Rule • For a window to have any

Basic Ideas • Open a window W with size |P| in the text. T

Preprocessing phase • T=GCATCGGCGAGAGTATACAGTACG • P=GCAGAGAG • L(S): a set contains all prefixes of

Preprocessing: Construct a Suffix Tree PR: the reversal string of P. 1 2 8

When there is a match, how do we move the window? T GC AT

T GC AT C G CAGAGAGT AT AC AGT AC G P GC AGAGAG

Find the longest suffix of W is also the prefix of pattern. T

T GC AT C G CAGGC AGT AT AC AGT AC G P GC

A Whole Example • T=GCATCGCAGAGA GTATACAGTACG • P=GCAGAGAG • First attempt : T GCATCGCAGAGAGTATACAGTACG

Second attempt : T GC AT C G CAGAGAGT AT AC AGT AC G

Third attempt: T GC AT C G CAGAGAGT AT AC AGT AC G P

Conclusion • Preprocessing phase is O(m). • Searching phase is O(mn). 15

Reference • [A 90]Algorithms for finding patterns in strings, A. V. Aho, Handbook of

Slides: 16

Download presentation

Reverse Factor Algorithm Speeding up on two string matching algorithms, Algorithmica, Vol. 12, 1994, pp. 247 -267 CROCHEMORE, M. , CZUMAJ, A. , GASIENIEC, L. , JAROMINEK, S. , LECROQ, T. , PLANDOWSKI, W. and RYTTER, W. Advisor: Prof. R. C. T. Lee Speaker: L. C. Chen 1

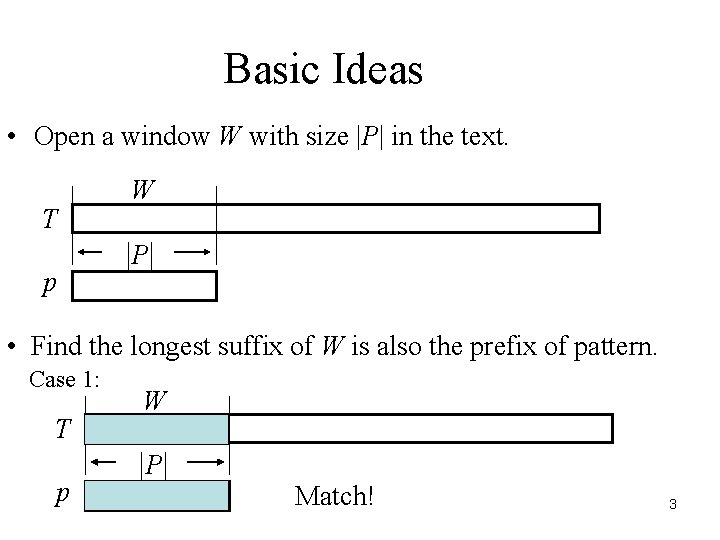
Rule 1: The Suffix to Prefix Rule • For a window to have any chance to match a pattern, in some way, there must be a suffix of the window which is equal to a prefix of the pattern. 2

Basic Ideas • Open a window W with size |P| in the text. T p W |P | • Find the longest suffix of W is also the prefix of pattern. Case 1: T p W |P | Match! 3

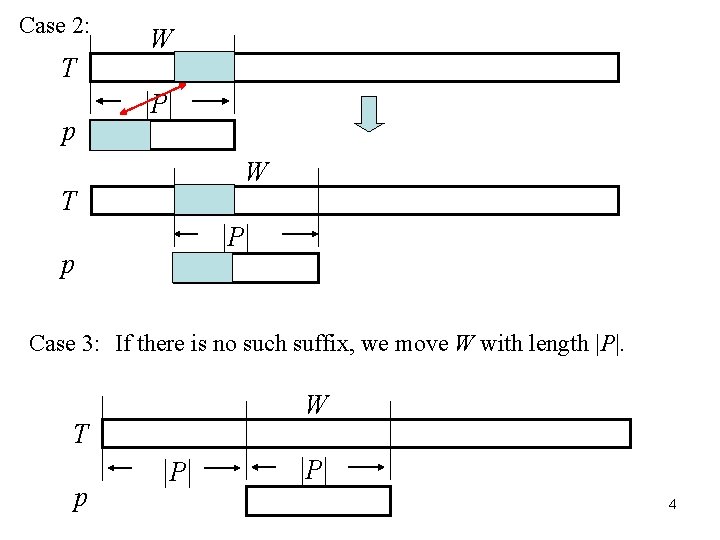
Case 2: T p W |P | W T |P | p Case 3: If there is no such suffix, we move W with length |P|. W T p |P | 4

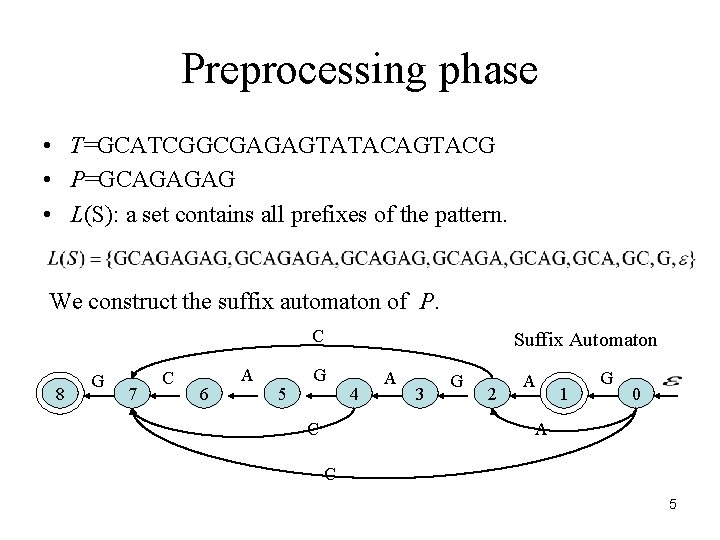
Preprocessing phase • T=GCATCGGCGAGAGTATACAGTACG • P=GCAGAGAG • L(S): a set contains all prefixes of the pattern. We construct the suffix automaton of P. C 8 G 7 C 6 A 5 Suffix Automaton G C 4 A 3 G 2 A 1 G 0 A C 5

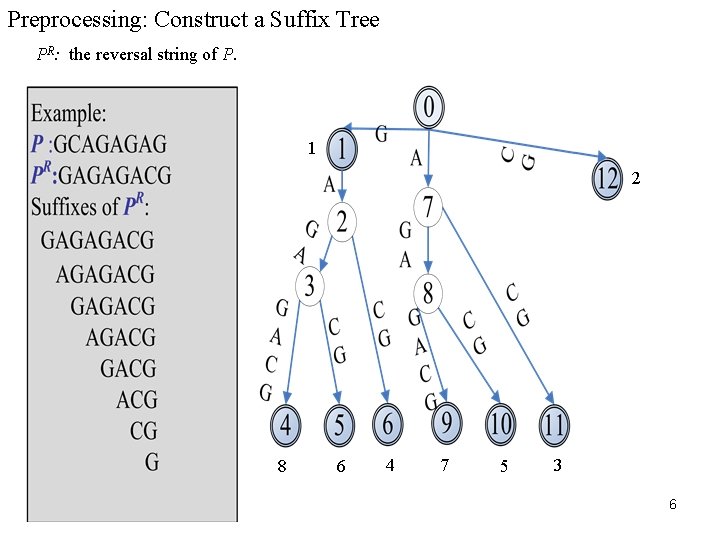
Preprocessing: Construct a Suffix Tree PR: the reversal string of P. 1 2 8 6 4 7 5 3 6

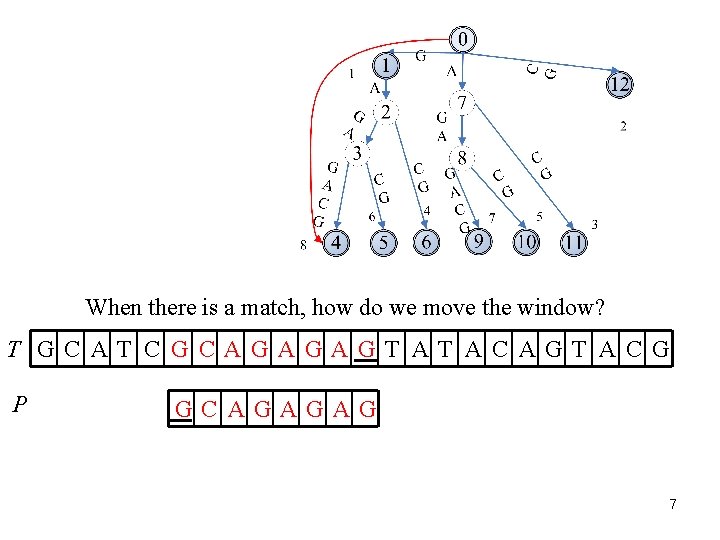
When there is a match, how do we move the window? T GC AT C G CAGAGAGT AT AC AGT AC G P GC AGAGAG 7

T GC AT C G CAGAGAGT AT AC AGT AC G P GC AGAGAG 8

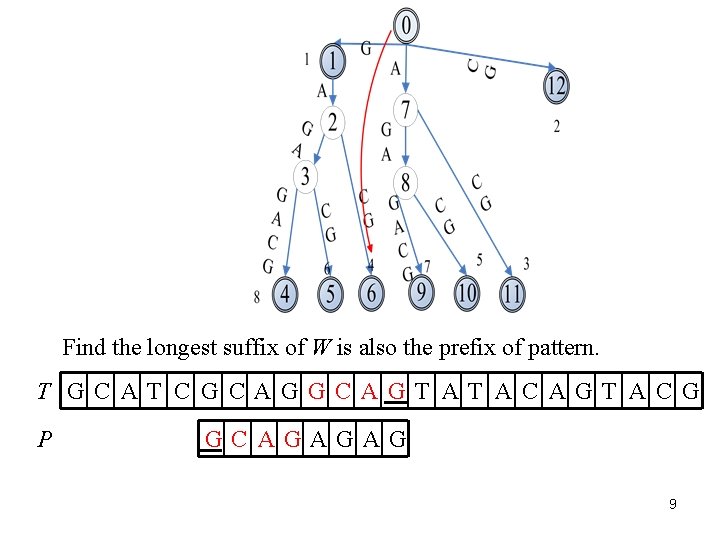
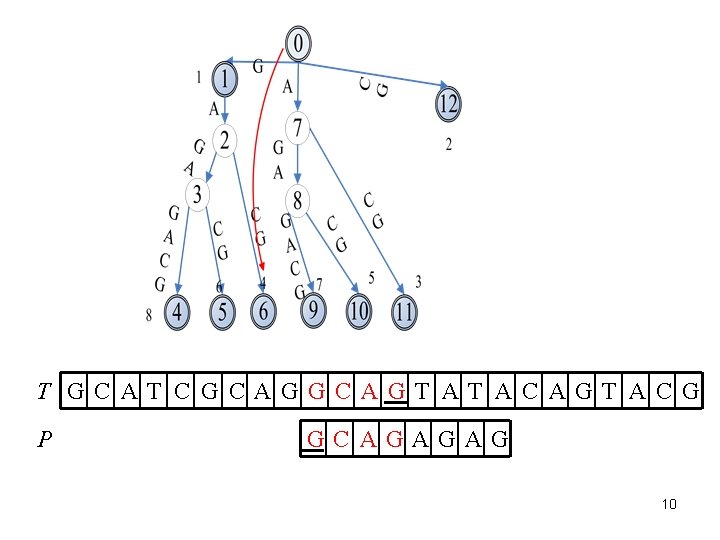
Find the longest suffix of W is also the prefix of pattern. T GC AT C G CAGGC AGT AT AC AGT AC G P GC AGAGAG 9

T GC AT C G CAGGC AGT AT AC AGT AC G P GC AGAGAG 10

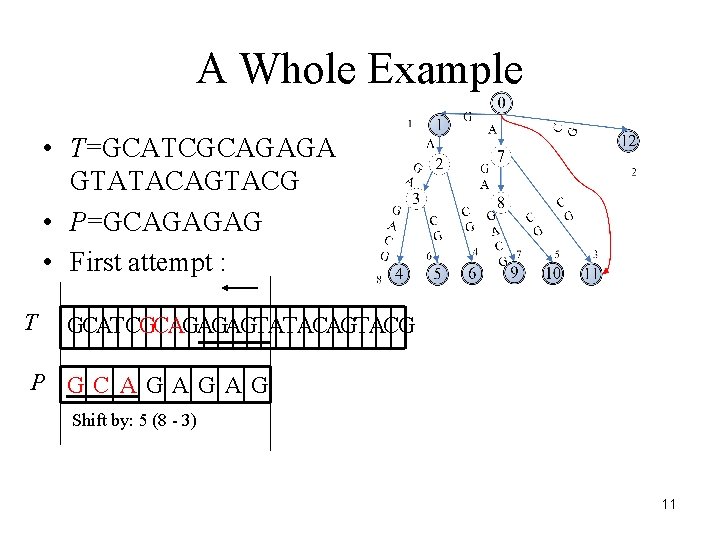
A Whole Example • T=GCATCGCAGAGA GTATACAGTACG • P=GCAGAGAG • First attempt : T GCATCGCAGAGAGTATACAGTACG P GC AGAGAG Shift by: 5 (8 - 3) 11

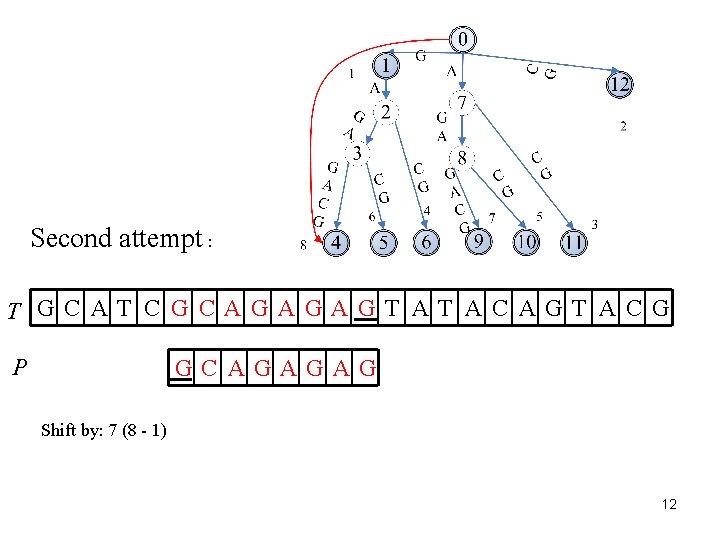
Second attempt : T GC AT C G CAGAGAGT AT AC AGT AC G P GC AGAGAG Shift by: 7 (8 - 1) 12

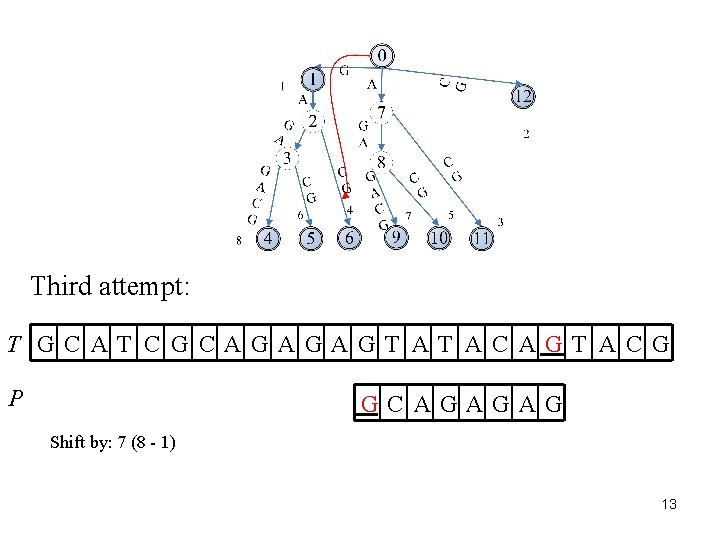
Third attempt: T GC AT C G CAGAGAGT AT AC AGT AC G P GC AGAGAG Shift by: 7 (8 - 1) 13

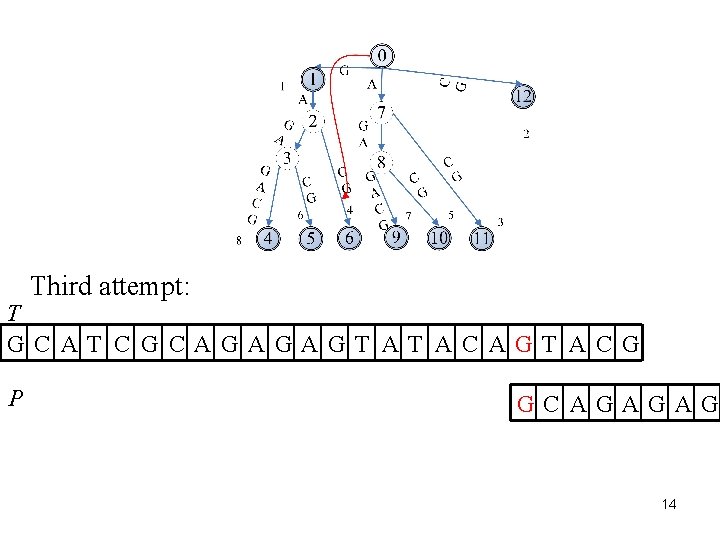
Third attempt: T GC AT C G CAGAGAGT AT AC AGT AC G P GC AGAGAG 14

Conclusion • Preprocessing phase is O(m). • Searching phase is O(mn). 15

Reference • [A 90]Algorithms for finding patterns in strings, A. V. Aho, Handbook of Theoretical Computer Science, Vol. A, Elsevier, Amsterdam, 1990, pp. 255 -300. • [A 85]The myriad virtues of suffix trees, Apostolico, A. , Combinatorial Algorithms on words, NATO Advanced Science Institutes, Series F, Vol. 12, 1985, pp. 85 -96 • [AG 86]The Boyer-Moore-Galil string searching strategies revisited, Apostolico, A. and Giancarlo, R. , SIAM, Comput. 15, 1986, pp 98 -105. • [BR 92]Average running time of the Boyer-Moore-Horspool algorithm, Baeza-Yates, R. A. and Regnier, M. Theoret. Comput. Sci. , 1992, pp. 19 -31. • [BKR 91]Analysis of algorithms and Data Structures, Banachowski, L. , Kreczmar, A. and Rytter, W. , Addison. Wesley. Reading, MA, 1991. 16