Retiming Outline Problem Formulation Retiming algorithm 1 Optimizing

Retiming Outline: • Problem • Formulation • Retiming algorithm 1

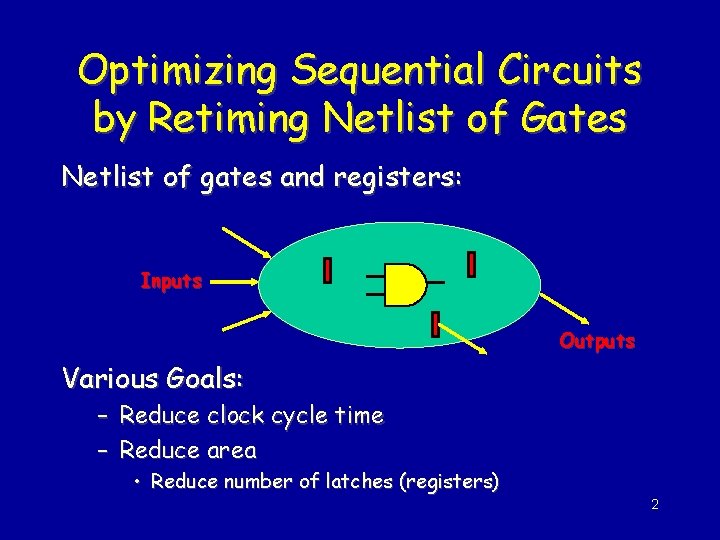
Optimizing Sequential Circuits by Retiming Netlist of Gates Netlist of gates and registers: Inputs Outputs Various Goals: – Reduce clock cycle time – Reduce area • Reduce number of latches (registers) 2

Retiming Problem – Pure combinational optimization can be myopic since relations across register boundaries are disregarded Solutions – Retiming: Move register(s) so that • clock cycle decreases, or number of registers decreases and • input-output behavior is preserved – Rn. R: Combine retiming with combinational optimization techniques • Move latches out of the way temporarily • optimize larger blocks of combinational 3

Circuit Represetation [Leiserson, Rose and Saxe (1983)] Circuit representation: G(V, E, d, w) – – V set of gates E set of wires d(v) = delay of gate/vertex v, (d(v) 0) w(e) = number of registers on edge e, (w(e) 0) 4

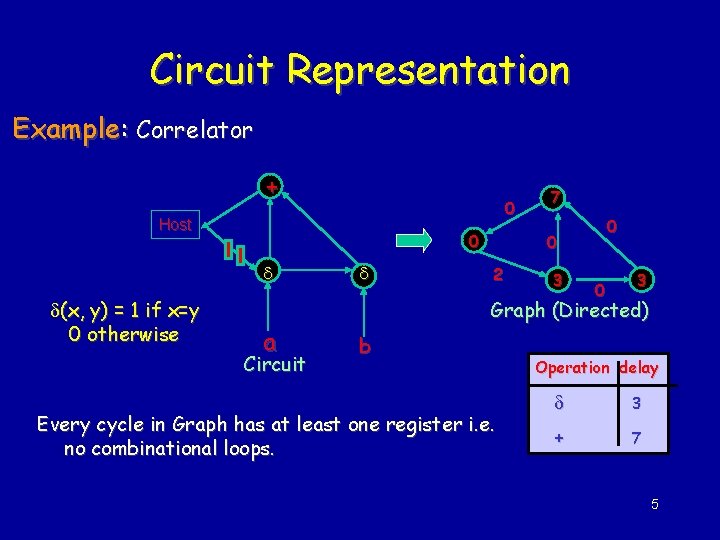
Circuit Representation Example: Correlator + 0 Host 0 (x, y) = 1 if x=y 0 otherwise 7 0 0 2 3 0 3 Graph (Directed) a Circuit b Every cycle in Graph has at least one register i. e. no combinational loops. Operation delay 3 + 7 5

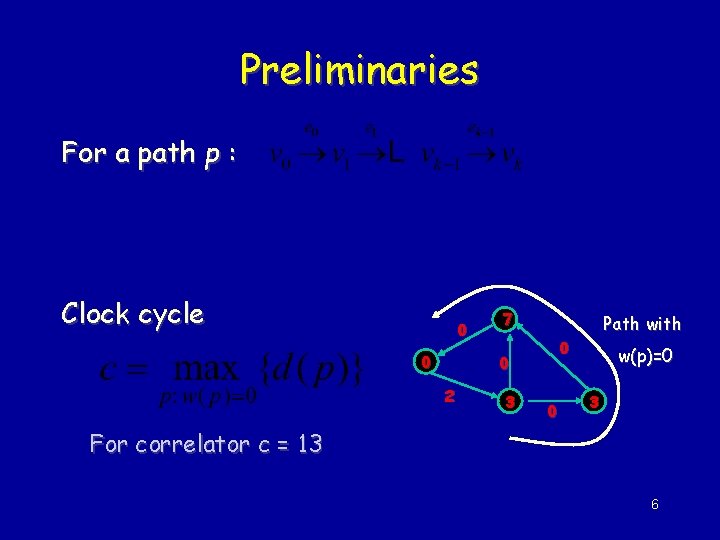
Preliminaries For a path p : Clock cycle 0 0 7 Path with 0 0 2 3 0 w(p)=0 3 For correlator c = 13 6

Basic Operation • Movement of registers from input to output of a gate or vice versa Retime by -1 Retime by 1 • Does not affect gate functionalities • A mathematical definition: retardation – r: V Z, an integer vertex labeling – wr(e) = w(e) + r(v) - r(u) for edge e = (u, v) 7

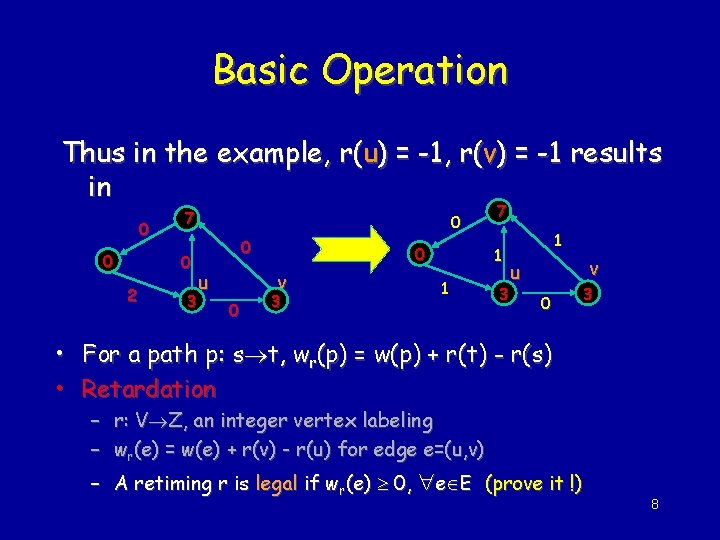
Basic Operation Thus in the example, r(u) = -1, r(v) = -1 results in 0 0 7 0 2 3 0 0 u 0 v 0 3 7 1 1 3 1 v u 0 3 • For a path p: s t, wr(p) = w(p) + r(t) - r(s) • Retardation – r: V Z, an integer vertex labeling – wr(e) = w(e) + r(v) - r(u) for edge e=(u, v) – A retiming r is legal if wr(e) 0, e E (prove it !) 8

Retiming for minimum clock cycle Problem Statement: (minimum cycle time) Given G (V, E, d, w), find a legal retiming r so that is minimized Retiming: 2 important matrices • Register weight matrix • Delay matrix 9

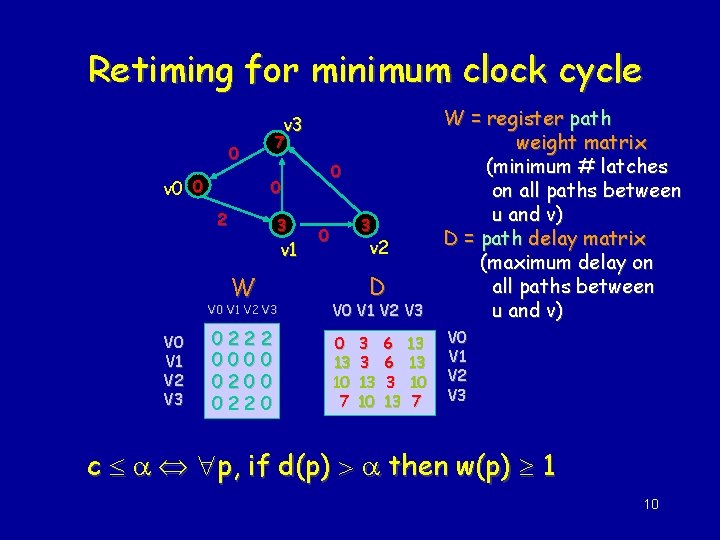
Retiming for minimum clock cycle V 0 V 1 V 2 V 3 W = register path weight matrix (minimum # latches on all paths between u and v) D = path delay matrix (maximum delay on all paths between u and v) 0222 0000 0220 0 13 10 7 V 0 V 1 V 2 V 3 v 3 7 0 v 0 0 0 2 3 v 1 W V 0 V 1 V 2 V 3 0 v 2 D 3 3 13 10 6 6 3 13 10 7 c p, if d(p) then w(p) 1 10

Conditions for Retiming Assume that we are asked to check if a retiming exists for a clock cycle Legal retiming: wr(e) 0 for all e. Hence wr(e) = w(e) + r(v) - r(u) 0 or r (u) - r (v) w (e) For all paths p: u v such that d(p) , we require wr(p) 1 – Thus Or take the least w(p) (tightest constraint) r(u)-r(v) W(u, v)-1 Note: this is independent of the path from u to v, so we just need to apply it to u, v such that D(u, v) 11

Solving the constraints • All constraints in difference-of-2 -variable form • Related to longest/shortest path problem W V 0 V 1 V 2 V 3 Correlator: = 7 D>7: Legal: r(u)-r(v) w(e) r(u)-r(v) W(u, v)-1 V 0 V 1 V 2 V 3 D V 0 V 1 V 2 V 3 0222 0000 0220 0 v 0 0 0 13 10 7 7 3 3 13 10 13 13 10 7 v 3 0 0 2 6 6 3 13 3 v 1 0 3 V 2 12 V 0 V 1 V 2 V 3

Solving the constraints • Do shortest path on constraint graph: (O(|V|3 )). • A solution exists if and only if there exists no negative weighted cycle. D>7: Legal: r(u)-r(v) w(e) r(u)-r(v) W(u, v)-1 r(0) -1 0 -1 2 0 -1 r(2) -1 1 1 0, -1 1 r(1) 0, -1 r(3) 0 Constraint graph A solution is r(v 0) = r(v 3) = 0, r(v 1) = r(v 2) = -1 13

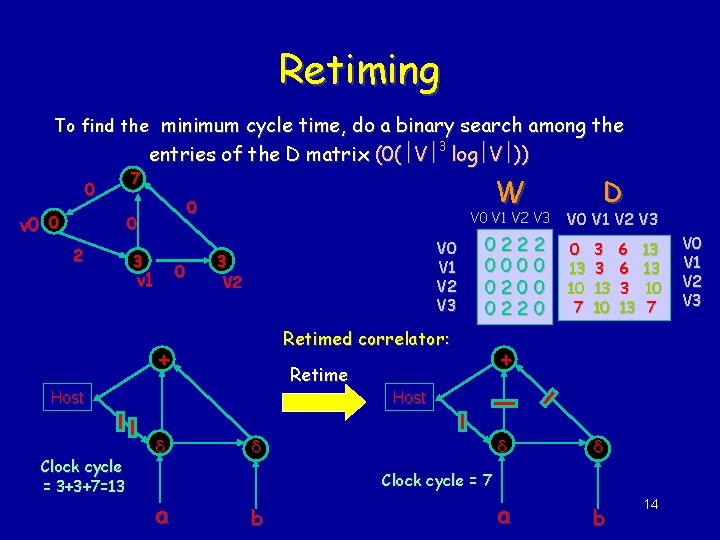
Retiming To find the minimum cycle time, do a binary search among the 0 v 0 0 7 entries of the D matrix (0( V 3 log V )) 0 2 W 0 3 0 v 1 V 0 V 1 V 2 V 3 3 V 2 Retimed correlator: + Retime Host Clock cycle = 3+3+7=13 0222 0000 0220 D V 0 V 1 V 2 V 3 0 13 10 7 3 3 13 10 6 6 3 13 10 7 + Host Clock cycle = 7 a b 14 V 0 V 1 V 2 V 3

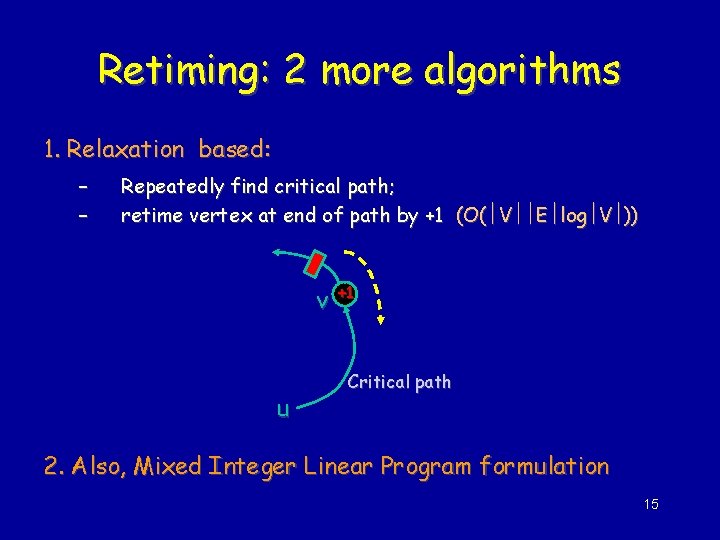
Retiming: 2 more algorithms 1. Relaxation based: – – Repeatedly find critical path; retime vertex at end of path by +1 (O( V E log V )) v u +1 Critical path 2. Also, Mixed Integer Linear Program formulation 15

Retiming for minimum area (minimum # latches) Goal: minimize number of registers used where av is a constant. 16

Minimum registers formulation Minimize: Subject to: wr(e) =w(e) + r(v) - r(u) 0 • Reducible to a flow problem 17