Response to Intervention RTI Best Practices in Mathematics

Response to Intervention RTI: Best Practices in Mathematics Interventions: An Introduction Jim Wright www. interventioncentral. org

Response to Intervention RTI & Math Interventions: Workshop Agenda Math Interventions: An Overview of the Research Basic Elements of RTI: A Foundation for Math Interventions Methods to Assess and Measure Student Progress in Mathematics Internet Resources for Math Assessment & Interventions www. interventioncentral. org

Response to Intervention Quick Check: What Are Common Concerns in Your School in the Area of ‘Math Interventions’? • Discuss the issues of student math performance and math interventions in your school. • What are your major challenges in these areas? www. interventioncentral. org 3

Response to Intervention www. interventioncentral. org National Mathematics Advisory Panel Report 13 March 2008 4

Response to Intervention Math Advisory Panel Report at: http: //www. ed. gov/mathpanel www. interventioncentral. org 5

Response to Intervention 2008 National Math Advisory Panel Report: Recommendations • “The areas to be studied in mathematics from pre-kindergarten through eighth grade should be streamlined and a well-defined set of the most important topics should be emphasized in the early grades. Any approach that revisits topics year after year without bringing them to closure should be avoided. ” • “Proficiency with whole numbers, fractions, and certain aspects of geometry and measurement are the foundations for algebra. Of these, knowledge of fractions is the most important foundational skill not developed among American students. ” • “Conceptual understanding, computational and procedural fluency, and problem solving skills are equally important and mutually reinforce each other. Debates regarding the relative importance of each of these components of mathematics are misguided. ” Source: National Mathshould Panel Fact develop Sheet. (Marchimmediate 2008). Retrieved recall on Marchof 14, arithmetic 2008, from • “Students facts http: //www. ed. gov/about/bdscomm/list/mathpanel/report/final-factsheet. html to free the “working memory” for solving more complex www. interventioncentral. org 6

Response to Intervention An RTI Challenge: Limited Research to Support Evidence-Based Math Interventions “… in contrast to reading, core math programs that are supported by research, or that have been constructed according to clear research-based principles, are not easy to identify. Not only have exemplary core programs not been identified, but also there are no tools available that we know of that will help schools analyze core math programs to determine their alignment with Source: Clarke, B. , Baker, S. , & Chard, D. (2008). Best practices in mathematics assessment and clearwithresearch-based principles. ” p. practices 459 in school intervention elementary students. In A. Thomas & J. Grimes (Eds. ), Best psychology V (pp. 453 -463). www. interventioncentral. org 7

Response to Intervention Math Intervention Planning: Some Challenges for Elementary RTI Teams • There is no national consensus about what math instruction should look like in elementary schools • Schools may not have consistent expectations for the ‘best practice’ math instruction strategies that teachers should routinely use in the classroom • Schools may not have a full range of assessment methods to collect baseline and progress monitoring data on math difficulties www. interventioncentral. org 8

Response to Intervention 1. Profile of Students With Significant Math Difficulties Spatial organization. The student commits errors such as misaligning numbers in columns in a multiplication problem or confusing directionality in a subtraction problem (and subtracting the original number—minuend— from the figure to be subtracted (subtrahend). 2. Visual detail. The student misreads a mathematical sign or leaves out a decimal or dollar sign in the answer. 3. Procedural errors. The student skips or adds a step in a computation sequence. Or the student misapplies a learned rule from one arithmetic procedure when completing another, different arithmetic procedure. 4. Inability to ‘shift psychological set’. The student does not shift from one operation type (e. g. , addition) to another (e. g. , multiplication) when warranted. 5. Graphomotor. The student’s poor handwriting can cause him or her to misread handwritten numbers, leading to errors in computation. 6. Memory. The student fails to remember a specific math fact needed to solve a problem. (The student may KNOW the math fact but not be able to recall it at ‘point of performance’. ) 7. Judgment and reasoning. The student comes up with solutions to problems are Arithmetic clearly unreasonable. However, student is not able Source: Rourke, B. that P. (1993). disabilities, specific & otherwise: the A neuropsychological perspective. Journal to of Learning Disabilities, 26, 214 -226. to gauge whether they actually adequately evaluate those responses www. interventioncentral. org 9

Response to Intervention Quick Check: Using the Student Profile of Math Difficulties in Problem-Solving • Review the Profile of Math Difficulties slide. • How can your school use this profile as a tool or resource to better focus your own math problem-solving efforts? Profile of Math Difficulties 1. Spatial organization. 2. Visual detail. 3. Procedural errors. 4. Inability to ‘shift psychological set’. 5. Graphomotor. 6. Memory. 7. Judgment and reasoning. www. interventioncentral. org 10

Response to Intervention “Mathematics is made of 50 percent formulas, 50 percent proofs, and 50 percent imagination. ” –Anonymous www. interventioncentral. org 11

Response to Intervention Who is At Risk for Poor Math Performance? : A Proactive Stance “…we use the term mathematics difficulties rather than mathematics disabilities. Children who exhibit mathematics difficulties include those performing in the low average range (e. g. , at or below the 35 th percentile) as well as those performing well below average…Using higher percentile cutoffs increases the likelihood that young children who go on to have serious math problems will be picked up in the screening. ” p. 295 Source: Gersten, R. , Jordan, N. C. , & Flojo, J. R. (2005). Early identification and interventions for students with mathematics difficulties. Journal of Learning Disabilities, 38, 293 -304. www. interventioncentral. org 12

Response to Intervention The Elements of Mathematical Proficiency: What the Experts Say… www. interventioncentral. org

Response to Intervention 5 Strands of Mathematical Proficiency 5 Big Ideas in Beginning Reading 1. Understanding 1. Phonemic Awareness 2. Computing 2. Alphabetic Principle 3. Applying 3. Fluency with Text 4. Reasoning 4. Vocabulary 5. Engagement Source: National Research Council. (2002). 5. Comprehension Source: Big ideas in beginning reading. University of Oregon. Retrieved Helping children learn mathematics. September 23, 2007, from Mathematics Learning Study Committee, J. http: //reading. uoregon. edu/index. php Kilpatrick & J. Swafford, Editors, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press. www. interventioncentral. org 14

Response to Intervention Five Strands of Mathematical Proficiency 1. Understanding: Comprehending mathematical concepts, operations, and relations--knowing what mathematical symbols, diagrams, and procedures mean. 2. Computing: Carrying out mathematical procedures, such as adding, subtracting, multiplying, and dividing numbers flexibly, accurately, efficiently, and appropriately. 3. Applying: Being able to formulate problems Source: National Research Council. (2002). Helping children learn mathematics. Mathematics mathematically and to devise strategies for Learning Study Committee, J. Kilpatrick & J. Swafford, Editors, Center for Education, Division of Behavioralsolving and Social Sciences and using Education. Washington, DC: National Press. them concepts and. Academy procedures www. interventioncentral. org 15

Response to Intervention Five Strands of Mathematical Proficiency (Cont. ) 4. Reasoning: Using logic to explain and justify a solution to a problem or to extend from something known to something less known. 5. Engaging: Seeing mathematics as sensible, useful, and doable—if you work at it—and being willing to do the work. Source: National Research Council. (2002). Helping children learn mathematics. Mathematics Learning Study Committee, J. Kilpatrick & J. Swafford, Editors, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press. www. interventioncentral. org 16

Response to Intervention Table Activity: Evaluate Your School’s Math Proficiency… • • • As a group, review the National Research Council ‘Strands of Math Proficiency’. Which strand do you feel that your school / curriculum does the best job of helping students to attain proficiency? Which strand do you feel that your school / curriculum should put the greatest effort to figure out how to help students to attain proficiency? Five Strands of Mathematical Proficiency (NRC, 2002) 1. Understanding: Comprehending mathematical concepts, operations, and relations--knowing what mathematical symbols, diagrams, and procedures mean. 2. Computing: Carrying out mathematical procedures, such as adding, subtracting, multiplying, and dividing numbers flexibly, accurately, efficiently, and appropriately. 3. Applying: Being able to formulate problems mathematically and to devise strategies for solving them using concepts and procedures appropriately. 4. Reasoning: Using logic to explain and justify a solution to a problem or to extend from something known to something less known. www. interventioncentral. org 5. Engaging: Seeing mathematics as sensible, 17

Response to Intervention Three General Levels of Math Skill Development (Kroesbergen & Van Luit, 2003) As students move from lower to higher grades, they move through levels of acquisition of math skills, to include: • Number sense • Basic math operations (i. e. , addition, subtraction, multiplication, division) • Problem-solving skills: “The solution of both verbal and nonverbal problems through the application of previously acquired information” (Kroesbergen & Van Luit, 2003, p. 98) Source: Kroesbergen, E. , & Van Luit, J. E. H. (2003). Mathematics interventions for children with special educational needs. Remedial and Special Education, 24, 97 -114. . www. interventioncentral. org 18

Response to Intervention Development of ‘Number Sense’ www. interventioncentral. org

Response to Intervention What is ‘Number Sense’? (Clarke & Shinn, 2004) “… the ability to understand the meaning of numbers and define different relationships among numbers. Children with number sense can recognize the relative size of numbers, use referents for measuring objects and events, and think and work with numbers in a flexible manner that treats numbers as a sensible system. ” p. 236 Source: Clarke, B. , & Shinn, M. (2004). A preliminary investigation into the identification and development of early mathematics curriculum-based measurement. School Psychology Review, 33, 234 – 248. www. interventioncentral. org 20

Response to Intervention What Are Stages of ‘Number Sense’? (Berch, 2005, p. 336) 1. Innate Number Sense. Children appear to possess ‘hard-wired’ ability (neurological ‘foundation structures’) to acquire number sense. Children’s innate capabilities appear also to include the ability to ‘represent general amounts’, not specific quantities. This innate number sense seems to be characterized by skills at estimation (‘approximate numerical judgments’) and a counting system that can be described loosely as ‘ 1, 2, 3, 4, … a lot’. 2. Acquired Number Sense. Young students learn through indirect and direct instruction to count specific objects beyond four and to internalize a number line as a mental representation of those Source: Berch, D. B. (2005). Making sense of number sense: Implications for children with mathematical precise number values. disabilities. Journal of Learning Disabilities, 38, 333 -339. . . www. interventioncentral. org 21

Response to Intervention 1. 2. Task Analysis of Number Sense & Operations (Methe & Riley-Tillman, 2008) Counting Comparing and Ordering: Ability to compare relative amounts e. g. , more or less than; ordinal numbers: e. g. , first, second, third) 3. Equal partitioning: Dividing larger set of objects into ‘equal parts’ 4. Composing and decomposing: Able to create different subgroupings of larger sets (for example, stating that a group of 10 objects can be broken down into 6 objects and 4 objects or 3 objects and 7 objects) 5. Grouping and place value: “abstractly grouping objects into sets of 10” (p. 32) in base-10 counting system. Methe, S. A. , & Riley-Tillman, T. C. (2008). An informed approach selecting and 6. Source: Adding to/taking away: Ability to add andtosubtract designing early mathematics interventions. School Psychology Forum: Research into amounts “by using accurate strategies that do www. interventioncentral. org Practice, 2, 29 -41. from sets 22

Response to Intervention Children’s Understanding of Counting Rules The development of children’s counting ability depends upon the development of: • One-to-one correspondence: “one and only one word tag, e. g. , ‘one, ’ ‘two, ’ is assigned to each counted object”. • Stable order: “the order of the word tags must be invariant across counted sets”. • Cardinality: “the value of the final word tag represents the quantity of items in the counted set”. • Abstraction: “objects of any kind can be collected together and counted”. • Order irrelevance: “items within a given set can be tagged in any sequence”. Source: Geary, D. C. (2004). Mathematics and learning disabilities. Journal of Learning Disabilities, 37, 415. www. interventioncentral. org 23

Response to Intervention Math Computation: Building Fluency Jim Wright www. interventioncentral. org

Response to Intervention "Arithmetic is being able to count up to twenty without taking off your shoes. " –Anonymous www. interventioncentral. org 25

Response to Intervention Benefits of Automaticity of ‘Arithmetic Combinations’ (Gersten, Jordan, & Flojo, 2005) • There is a strong correlation between poor retrieval of arithmetic combinations (‘math facts’) and global math delays • Automatic recall of arithmetic combinations frees up student ‘cognitive capacity’ to allow for understanding of higher-level problem-solving • By internalizing numbers as mental constructs, students can manipulate those numbers in their head, allowing for the intuitive understanding of arithmetic properties, such as associative property and. N. C. , commutative property Source: Gersten, R. , Jordan, & Flojo, J. R. (2005). Early identification and interventions for students with mathematics difficulties. Journal of Learning Disabilities, 38, 293 -304. www. interventioncentral. org 26

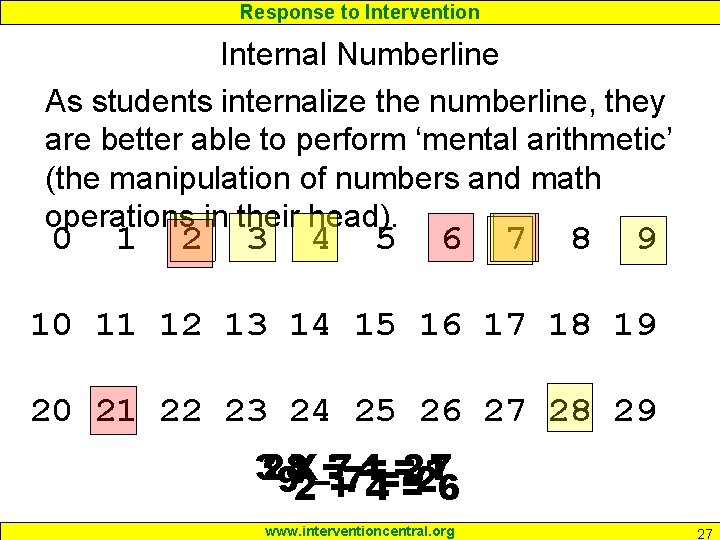
Response to Intervention Internal Numberline As students internalize the numberline, they are better able to perform ‘mental arithmetic’ (the manipulation of numbers and math operations in their head). 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 328 ÷ 774===21 7 9 X – 2 2+4=6 www. interventioncentral. org 27

Response to Intervention Associative Property • “within an expression containing two or more of the same associative operators in a row, the order of operations does not matter as long as the sequence of the operands is not changed” • Example: –(2+3)+5=10 – 2+(3+5)=10 Source: Associativity. Wikipedia. Retrieved September 5, 2007, from http: //en. wikipedia. org/wiki/Associative www. interventioncentral. org 28

Response to Intervention Commutative Property • “the ability to change the order of something without changing the end result. ” • Example: – 2+3+5=10 – 2+5+3=10 Source: Associativity. Wikipedia. Retrieved September 5, 2007, from http: //en. wikipedia. org/wiki/Commutative www. interventioncentral. org 29

Response to Intervention How much is 3 + 8? : Strategies to Least efficient strategy: Solve… Count out and group 3 objects; count out and group 8 objects; count all objects: =11 + More efficient strategy: Begin at the number 3 and ‘count up’ 8 more digits (often using fingers for counting): 3+8 More efficient strategy: Begin at the number 8 (larger number) and ‘count up’ 3 more digits: 8+ 3 combination is Most efficient strategy: ‘ 3 + 8’ arithmetic Answer = 11 stored in memory and automatically retrieved: Source: Gersten, R. , Jordan, N. C. , & Flojo, J. R. (2005). Early identification and interventions for students with mathematics difficulties. Journal of Learning Disabilities, 38, 293 -304. www. interventioncentral. org 30

Response to Intervention Comprehending Math Vocabulary: The Barrier of Abstraction “…when it comes to abstract mathematical concepts, words describe activities or relationships that often lack a visual counterpart. Yet studies show that children grasp the idea of quantity, as well as other relational concepts, from a very early age…. As children develop their capacity for understanding, language, and its vocabulary, becomes a vital cognitive link between a child’s natural sense of number and order and conceptual learning. ” Source: Chard, D. (n. d. . Vocabulary strategies for the mathematics classroom. Retrieved -Chard, D. from (n. d. ) November 23, 2007, http: //www. eduplace. com/state/pdf/author/chard_hmm 05. pdf. www. interventioncentral. org 31

Response to Intervention Developing Student Metacognitive Abilities www. interventioncentral. org

Response to Intervention Importance of Metacognitive Strategy Use… “Metacognitive processes focus on selfawareness of cognitive knowledge that is presumed to be necessary for effective problem solving, and they direct and regulate cognitive processes and strategies during problem solving…That is, successful problem solvers, consciously or unconsciously (depending on task demands), use self-instruction, selfquestioning, and self-monitoring to gain access to strategic knowledge, guide execution of strategies, and regulate use of Source: Montague, M. (1992). The effects of cognitive and metacognitive strategy instruction on the mathematical problem solving of middle school students with learning disabilities. Journal of strategies problem-solving Learning Disabilities, 25, 230 -248. and www. interventioncentral. org 33

Response to Intervention RTI Activity: Compile a Math Skills Checklist • Review the relevant powerpoint slides and information from this presentation. • At your tables, develop a draft ‘math skills checklist’ to use when consulting with teachers about students with math difficulties. • Be prepared to discuss your resulting checklist with the larger group. www. interventioncentral. org 34

Response to Intervention RTI & Intervention: Key Concepts www. interventioncentral. org

Response to Intervention Core Instruction, Interventions, Accommodations & Modifications: Sorting Them Out • Core Instruction. Those instructional strategies that are used routinely with all students in a general-education setting are considered ‘core instruction’. Highquality instruction is essential and forms the foundation of RTI academic support. NOTE: While it is important to verify that good core instructional practices are in place for a struggling student, those routine practices do not ‘count’ as individual student interventions. www. interventioncentral. org 36

Response to Intervention Core Instruction, Interventions, Accommodations & Modifications: Sorting Them Out • Intervention. An academic intervention is a strategy used to teach a new skill, build fluency in a skill, or encourage a child to apply an existing skill to new situations or settings. An intervention can be thought of as “a set of actions that, when taken, have demonstrated ability to change a fixed educational trajectory” (Methe & Riley-Tillman, 2008; p. 37). www. interventioncentral. org 37

Response to Intervention Core Instruction, Interventions, Accommodations & Modifications: Sorting Them Out • Accommodation. An accommodation is intended to help the student to fully access and participate in the general-education curriculum without changing the instructional content and without reducing the student’s rate of learning (Skinner, Pappas & Davis, 2005). An accommodation is intended to remove barriers to learning while still expecting that students will master the same instructional content as their typical peers. – Accommodation example 1: Students are allowed to supplement silent reading of a novel by listening to the book on tape. – Accommodation example 2: For unmotivated students, the instructor breaks larger assignments into smaller ‘chunks’ and providing students with www. interventioncentral. org 38

Response to Intervention Core Instruction, Interventions, Accommodations & Modifications: Sorting Them Out • Modification. A modification changes the expectations of what a student is expected to know or do—typically by lowering the academic standards against which the student is to be evaluated. Examples of modifications: – Giving a student five math computation problems for practice instead of the 20 problems assigned to the rest of the class – Letting the student consult course notes during a test when peers are not permitted to do so www. interventioncentral. org 39

Response to Intervention Big Ideas: The Four Stages of Learning Can Be Summed Up in the ‘Instructional Hierarchy’ pp. 2 -3 (Haring et al. , 1978) Student learning can be thought of as a multi-stage process. The universal stages of learning include: • Acquisition: The student is just acquiring the skill. • Fluency: The student can perform the skill but must make that skill ‘automatic’. • Generalization: The student must perform the skill across situations or settings. • Adaptation: The student confronts novel task demands that require that the student adapt a current skill to meet new requirements. Source: Haring, N. G. , Lovitt, T. C. , Eaton, M. D. , & Hansen, C. L. (1978). The fourth R: Research in the classroom. Columbus, OH: Charles E. Merrill Publishing Co. www. interventioncentral. org 40

Response to Intervention Increasing the Intensity of an Intervention: Key Dimensions Interventions can move up the RTI Tiers through being intensified across several dimensions, including: • • • Type of intervention strategy or materials used Student-teacher ratio Length of intervention sessions Frequency of intervention sessions Duration of the intervention period (e. g. , extending an intervention from 5 weeks to 10 weeks) • Motivation strategies Source: Burns, M. K. , & Gibbons, K. A. (2008). Implementing response-to-intervention in elementary and secondary schools. Routledge: New York. Kratochwill, T. R. , Clements, M. A. , & Kalymon, K. M. (2007). Response to intervention: Conceptual and methodological issues in implementation. In Jimerson, S. R. , Burns, M. K. , & Van. Der. Heyden, A. M. (Eds. ), Handbook of response to intervention: The science and practice of assessment and intervention. New York: Springer. www. interventioncentral. org 41

Response to Intervention RTI Interventions: What If There is No Commercial Intervention Package or Program Available? “Although commercially prepared programs and the subsequent manuals and materials are inviting, they are not necessary. … A recent review of research suggests that interventions are research based and likely to be successful, if they are correctly targeted and provide explicit instruction in the skill, an appropriate level of challenge, sufficient opportunities to respond to and practice the skill, and immediate feedback on performance…Thus, these [elements] could be used which to judge potentialin tier 2 Source: Burns, as M. K. , criteria & Gibbons, K. with A. (2008). Implementing response-to-intervention elementary and secondary schools. Routledge: New York. interventions. ” p. 88 www. interventioncentral. org 42

Response to Intervention Research-Based Elements of Effective Academic Interventions • ‘Correctly targeted’: The intervention is appropriately matched to the student’s academic or behavioral needs. • ‘Explicit instruction’: Student skills have been broken down “into manageable and deliberately sequenced steps and providing overt strategies for students to learn and practice new skills” p. 1153 • ‘Appropriate level of challenge’: The student experiences adequate success with the instructional task. • ‘High opportunity to respond’: The student actively responds at a rate frequent enough to promote Source: effective Burns, M. K. , learning. Van. Der. Heyden, A. M. , & Boice, C. H. (2008). Best practices in intensive academic interventions. In A. Thomas & J. Grimes (Eds. ), Best practices in school psychology V (pp. 1151 -1162). Bethesda, MD: National Association of School prompt Psychologists. • ‘Feedback’: The student receives www. interventioncentral. org 43

Response to Interventions: Potential ‘Fatal Flaws’ Any intervention must include 4 essential elements. The absence of any one of the elements would be considered a ‘fatal flaw’ (Witt, Van. Der. Heyden & Gilbertson, 2004) that blocks the school from drawing meaningful conclusions from the student’s response to the intervention: 1. Clearly defined problem. The student’s target concern is stated in specific, observable, measureable terms. This ‘problem identification statement’ is the most important step of the problem-solving model (Bergan, 1995), as a clearly defined problem allows the teacher or RTI Team to select a wellmatched intervention to address it. 2. Baseline data. The teacher or RTI Team measures the student’s academic skills in the target concern (e. g. , reading fluency, math computation) prior to beginning the intervention. Baseline data becomes the point of comparison throughout the intervention to help the school to determine whether that intervention is effective. 3. Performance goal. The teacher or RTI Team sets a specific, data-based goal for student improvement during the intervention and a checkpoint date by which the goal should be attained. 4. Progress-monitoring plan. The teacher or RTI Team collects student data Source: Witt, to J. C. , Van. Der. Heyden, A. M. , &the Gilbertson, D. (2004). Troubleshooting regularly determine whether student is on-track to reachbehavioral the interventions. A systematic performance goal. process for finding and eliminating problems. School Psychology Review, 33, 363 -383. www. interventioncentral. org 44

Response to Intervention RTI Activity: Essential Elements of Interventions • Review the information on ‘essential elements of interventions’ reviewed at this workshop. • How can your school use this information to ensure that quality math interventions are being used at each Tier of RTI? • Be prepared to share your findings with the large group. www. interventioncentral. org 45

Response to Intervention RTI: Math Assessment www. interventioncentral. org

Data Collection: Defining Terms Response to Intervention Evaluation. “the process of using information collected through assessment to make decisions or reach conclusions. ” (Hosp, 2008; p. 364). Example: A student can be evaluated for problems in ‘fluency with text’ by collecting information using various sources (e. g. , CBM ORF, teacher interview, direct observations of the student reading across settings, etc. ), comparing those results to peer norms or curriculum expectations, and making a decision about whether the Assessment. “theperformance process of collecting information about the student’s current is acceptable. characteristics of persons or objects by measuring them. ” (Hosp, 2008; p. 364). Example: The construct ‘fluency with text’ can be assessed using various measurements, including CBM ORF, teacher interview, and direct observations of the student reading in different settings and in Measurement. “the process of applying numbers to the different material. characteristics of objects or people in a systematic way” (Hosp, 2008; p. 364). Example: Curriculum-Based Measurement Oral Reading Fluency (CBM ORF) is onewww. interventioncentral. org method to measure the construct ‘fluency with 47

Response to Intervention Use Time & Resources Efficiently By Collecting Information Only on ‘Things That Are Alterable’ “…Time should be spent thinking about things that the intervention team can influence through instruction, consultation, related services, or adjustments to the student’s program. These are things that are alterable. …Beware of statements about cognitive processes that shift the focus from the curriculum and may even encourage questionable educational practice. They can also promote writing off a student because of Source: the Howell, K. W. , Hosp, J. that L. , & Kurns, S. (2008). Best practices in curriculum-based rationale the student’s insufficient evaluation. In A. Thomas & J. Grimes (Eds. ), Best practices in school psychology V (pp. 349 -362). Bethesda, MD: National Association of School performance is due to. Psychologists. a limited and fixed www. interventioncentral. org 48

Response to Intervention Formal Tests: Only One Source of Student Assessment Information “Tests are often overused and misunderstood in and out of the field of school psychology. When necessary, analog [i. e. , test] observations can be used to test relevant hypotheses within controlled conditions. Testing is a highly standardized form of observation. …. The only reason to administer a test is to answer well-specified questions and examine well-specified hypotheses. It is best practice to identify and make explicit the most relevant questions before assessment begins. …The process of assessment should follow these questions. Source: Christ, T. questions (2008). Best practices in problemnot analysis. In A. Thomas & J. Grimes (Eds. ), The should follow assessment. Best practices in school psychology V (pp. 159 -176). Bethesda, MD: National Association of “ p. 170 School Psychologists. www. interventioncentral. org 49

Response to Intervention Identifying and Measuring Complex Academic Problems at the Middle and High School Level: Discrete Categorization • Students with math deficits can present with a range of concerns that interfere with academic success. • One frequent challenge for these students is the need to reduce complex global academic goals into discrete subskills that can be individually measured and tracked over time. www. interventioncentral. org 50

Response to Intervention Discrete Categorization: A Strategy for Assessing Complex, Multi-Step Student Academic Tasks Definition of Discrete Categorization: ‘Listing a number of behaviors and checking off whether they were performed. ’ (Kazdin, 1989, p. 59). • Approach allows educators to define a larger ‘behavioral’ goal for a student and to break that goal down into sub-tasks. (Each sub-task should be defined in such a way that it can be scored as ‘successfully accomplished’ or ‘not accomplished’. ) • The constituent behaviors that make up the larger behavioral goal need not be directly related to each other. For example, ‘completed homework’ may include as sub-tasks ‘wrote down homework assignment correctly’ and ‘created a work plan before starting homework’ Source: Kazdin, A. E. (1989). Behavior modification in applied settings (4 ed. ). Pacific Gove, CA: th Brooks/Cole. . www. interventioncentral. org 51

Response to Intervention Discrete Categorization Example: Math Study Skills General Academic Goal: Improve John’s Performance on Math Word Problems John was struggling with word problems in the classroom. The teacher defined the essential elements of word problems, to include the following: q The student understands the relevant math vocabulary. q The student has the necessary reading skills to decode and comprehend the word problem. q The student understands the underlying math operations required to solve the math problem. q The student is able to first develop a plan before attempting to solve the math problem. q The student can check the work to verify calculations used in the math problem. www. interventioncentral. org 52

Response to Intervention Applications of Local Norm Data (Stewart & Silberglit, 2008) Local norm data can be used to: • Evaluate and improve the current core instructional program. • Allocate resources to classrooms, grades, and buildings where student academic needs are greatest. • Guide the creation of targeted Tier 2 (supplemental intervention) groups • Set academic goals for improvement for students on Tier 2 and Tier 3 interventions. • Move students across levels of intervention, based on performance relative to that of Source: Stewart, L. H. & Silberglit, B. (2008). Best practices in developing academic local norms. peers (local norms). In A. Thomas & J. Grimes (Eds. ), Best practices in school psychology V (pp. 225 -242). Bethesda, MD: National Association of School Psychologists. www. interventioncentral. org 53

Response to Intervention Curriculum-Based Measurement: Advantages as a Set of Tools to Monitor RTI/Academic Cases • Aligns with curriculum-goals and materials • Is reliable and valid (has ‘technical adequacy’) • Is criterion-referenced: sets specific performance levels for specific tasks • Uses standard procedures to prepare materials, administer, and score • Samples student performance to give objective, observable ‘lowinference’ information about student performance • Has decision rules to help educators to interpret student data and make appropriate instructional decisions • Is efficient to implement in schools (e. g. , training can be done quickly; the measures are brief and feasible for classrooms, etc. ) • Provides data that can be converted into visual displays for ease of communication Source: Hosp, M. K. , Hosp, J. L. , & Howell, K. W. (2007). The ABCs of CBM. New York: Guilford. www. interventioncentral. org 54

Response to Intervention Fluency/Accuracy Measures: RTI Math • Curriculum-Based Measurement: Early Math Fluency • CBM: Math Computation • CBM: NCTM Math Focal Points www. interventioncentral. org 55

Response to Intervention National Council of Teachers of Mathematics “What Are Curriculum Focal Points? Curriculum focal points are important mathematical topics for each grade level, pre-K– 8. These areas of instructional emphasis can serve as organizing structures for curriculum design and instruction at and across grade levels. The topics are central to mathematics: they convey knowledge and skills that are essential to educated citizens, and they provide the foundations for further mathematical learning. Because the focal points are core structures that lay a conceptual foundation, they can serve to organize content, connecting and bringing coherence to multiple concepts and processes taught at and across grade levels. They are indispensable elements in developing problem solving, reasoning, and critical thinking skills, which are important to all mathematics Source: NCTM. Retrieved from http: //www. nctm. org/standards/content. aspx? id=264. learning. ” www. interventioncentral. org 56

Response to Intervention RTI Activity: Draft a Plan to Select RTI Math Assessments • Review the different options discussed at this workshop for assessing student math skills. • Discuss how your school might proceed in selecting appropriate tools to screen students for math difficulties, as well as to monitor the progress of students on math interventions. www. interventioncentral. org 57