RESPONSE OF A DAMPED SYSTEM UNDER THE HARMONIC






















- Slides: 28

RESPONSE OF A DAMPED SYSTEM UNDER THE HARMONIC MOTION OF THE BASE

y(t) = Displacement of the base From the figure, the equation of motion is If , where

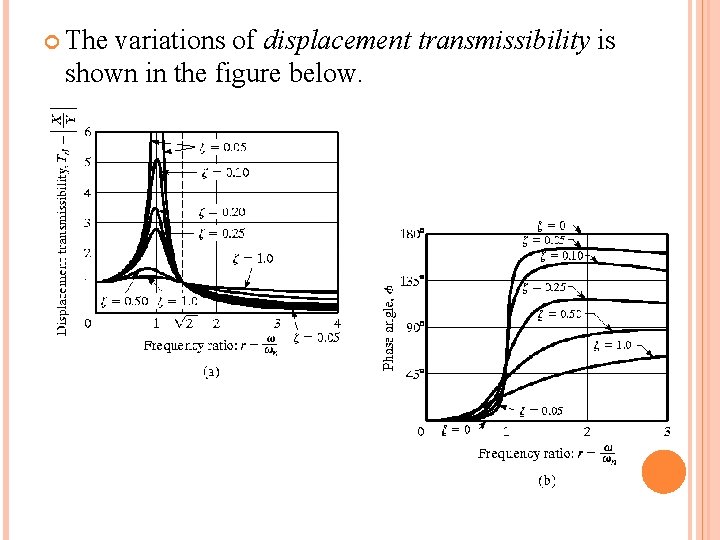
The steady-state response of the mass can be expressed as where OR using trigonometric identities, where Displacement transmissibility

If expressed in complex form, response of the system can be expressed as and the displacement transmissibility as Displacement transmissibility : The ratio of the amplitude of the response to that of the motion y(t).

The variations of displacement transmissibility is shown in the figure below.

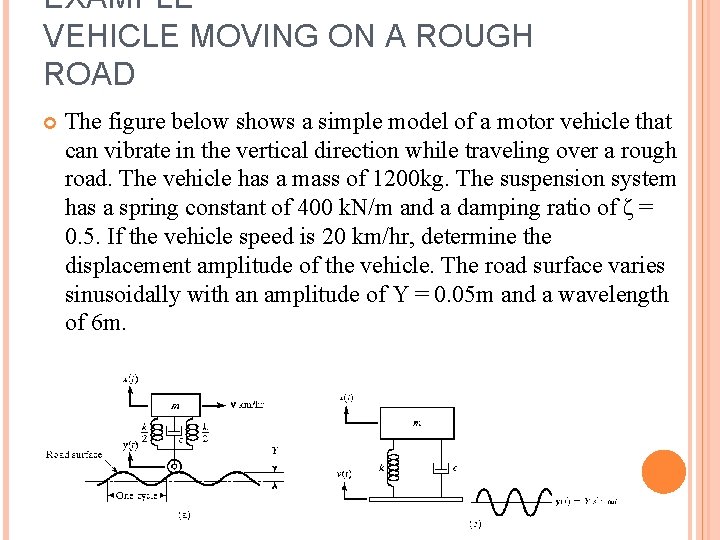
EXAMPLE VEHICLE MOVING ON A ROUGH ROAD The figure below shows a simple model of a motor vehicle that can vibrate in the vertical direction while traveling over a rough road. The vehicle has a mass of 1200 kg. The suspension system has a spring constant of 400 k. N/m and a damping ratio of ζ = 0. 5. If the vehicle speed is 20 km/hr, determine the displacement amplitude of the vehicle. The road surface varies sinusoidally with an amplitude of Y = 0. 05 m and a wavelength of 6 m.

SOLUTION The frequency can be found by For v = 20 km/hr, ω = 5. 81778 rad/s. The natural frequency is given by, Hence, the frequency ratio is 7

SOLUTION CON’T The amplitude ratio can be found from Eq. (3. 68): 8 Thus, the displacement amplitude of the vehicle is given by This indicates that a 5 cm bump in the road is transmitted as a 7. 3 cm bump to the chassis and the passengers of the car.

VIBRATION UNDER GENERAL FORCING CONDITIONS

INTRODUCTION A general forcing function may be periodic (nonharmonic) or nonperiodic. A nonperiodic forcing function may be acting for a short, long, or infinite duration. Shock is defined as the small forcing function or excitation as compared to the natural time period of the system. Some examples of general forcing functions include the motion imparted by a cam to the follower; the vibration felt by an instrument when its package is dropped from a height; etc. The transient response of a system can be found by using what is known as the convolution integral.

RESPONSE UNDER A GENERAL PERIODIC FORCE The equation of motion can be expressed as The steady-state solution of the equation is derived as:

RESPONSE UNDER A NONPERIODIC FORCE When the exciting force F(t) is nonperiodic, such as that due to the blast from an explosion, a different method of calculating the response is required. Various methods can be used to find the response of the system to an arbitrary excitation. Some of these methods are as follows: 1. 2. 3. 4. 5. Representing the excitation by a Fourier integral Using the method of convolution integral Using the method of Laplace transforms First approximating F(t) by a suitable interpolation model and then using a numerical procedure Numerically integrating the equation of motion.

CONVOLUTION INTEGRAL By designating the magnitude of the impulse we can write, in general, A unit impulse is defined as by F,

CONVOLUTION INTEGRAL • Response to an impulse For an undamped system, the solution of the equation of motion is given by Eq. (2. 27) as where 14

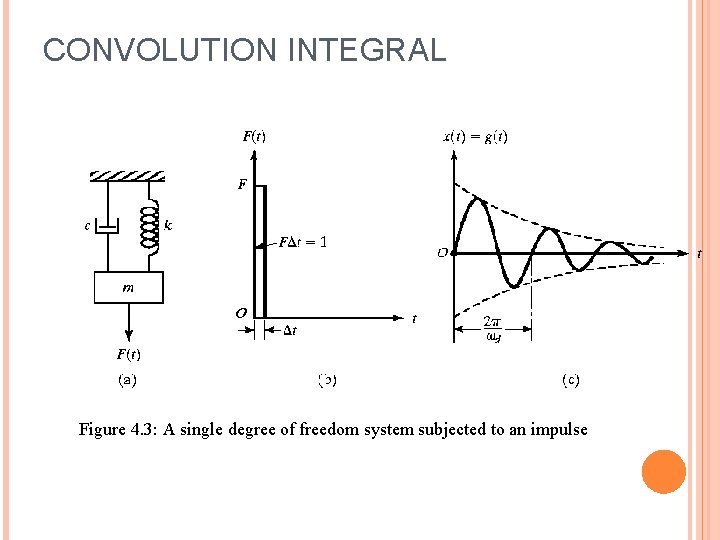
CONVOLUTION INTEGRAL Figure 4. 3: A single degree of freedom system subjected to an impulse 15

CONVOLUTION INTEGRAL If the mass is at rest before the unit impulse is applied, we obtain, from the impulse-momentum relation, Thus the initial conditions are given by Hence, Eq. (4. 21) reduces to 16

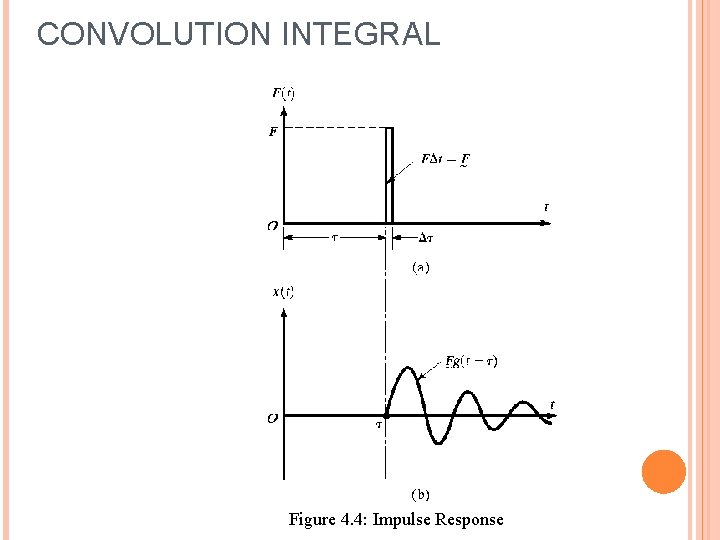
CONVOLUTION INTEGRAL which is also known as the impulse response function. The Eq. (4. 27) is shown in Fig. 4. 3(c). If the magnitude of the impulse is instead of unity, the initial velocity is and the response of the system becomes If the impulse is applied at an arbitrary time t = τ, it will change the velocity at t = τ, shown in Fig. 4. 4(a). Thus, 17

CONVOLUTION INTEGRAL Figure 4. 4: Impulse Response 18

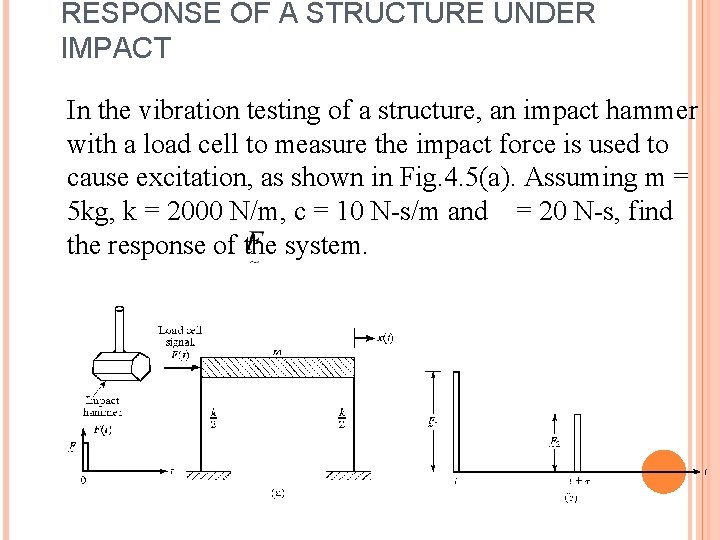
RESPONSE OF A STRUCTURE UNDER IMPACT In the vibration testing of a structure, an impact hammer with a load cell to measure the impact force is used to cause excitation, as shown in Fig. 4. 5(a). Assuming m = 5 kg, k = 2000 N/m, c = 10 N-s/m and = 20 N-s, find the response of the system. 19

SOLUTION From the known data, we can compute, 20 Assuming that the impact is given at t = 0, we find the response of the system as

CONVOLUTION INTEGRAL • Response to General Forcing Condition Consider the response of the system under an arbitrary external force, shown in Fig. 4. 6. Hence, the response is given by Fig. 4. 6: An arbitrary (nonperiodic) forcing function 21

CONVOLUTION INTEGRAL The total response at time t can be found by summing all the responses due to the elementary impulses acting at all times τ: Letting and replacing the summation by integration, we obtain which is called the convolution or Duhamel integral. 22

TWO DEGREE OF FREEDOM SYSTEMS

INTRODUCTION As is evident from the systems shown in Figs. 5. 1 and 5. 2, the configuration of a system can be specified by a set of independent coordinates termed as generalized coordinates, such as length, angle, or some other physical parameters. Principle coordinates is defined as any set of coordinates that leads a coupled equation of motion to an uncoupled system of equations. 24

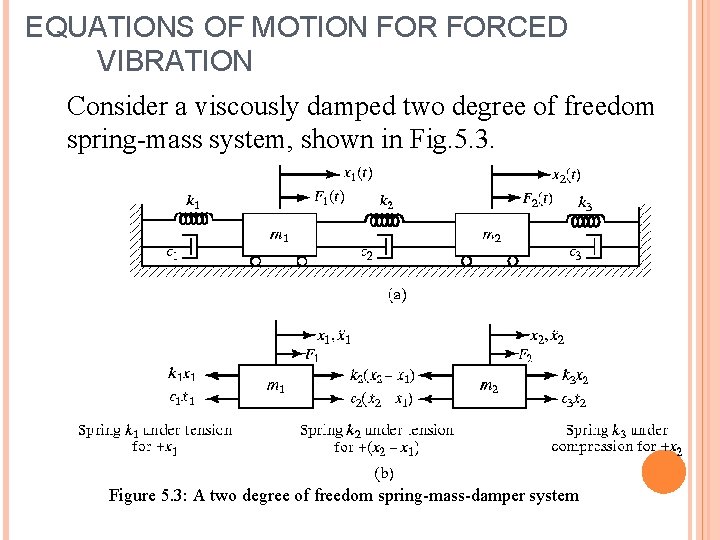
EQUATIONS OF MOTION FORCED VIBRATION Consider a viscously damped two degree of freedom spring-mass system, shown in Fig. 5. 3. Figure 5. 3: A two degree of freedom spring-mass-damper system

EQUATIONS OF MOTION FORCED VIBRATION The application of Newton’s second law of motion to each of the masses gives the equations of motion: 26 Both equations can be written in matrix form as where [m], [c], and [k] are called the mass, damping, and stiffness matrices, respectively, and are given by

EQUATIONS OF MOTION FORCED VIBRATION 27 And the displacement and force vectors are given respectively: It can be seen that the matrices [m], [c], and [k] are symmetric:

EQUATIONS OF MOTION FORCED VIBRATION where the superscript T denotes the transpose of the matrix. The solution of Eqs. (5. 1) and (5. 2) involves four constants of integration (two for each equation). We shall first consider the free vibration solution of Eqs. (5. 1) and (5. 2). 28
 Damped system under harmonic force
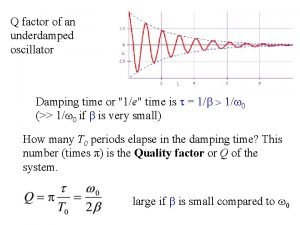
Damped system under harmonic force Q factor damped harmonic oscillator
Q factor damped harmonic oscillator Heavy damping equation
Heavy damping equation First harmonic and second harmonic
First harmonic and second harmonic Number of degrees of freedom
Number of degrees of freedom Damped free vibration
Damped free vibration Second order differential equation
Second order differential equation Damped pendulum equation of motion
Damped pendulum equation of motion Damped trigonometric functions
Damped trigonometric functions General equation of shm
General equation of shm Oscillation
Oscillation Damped oscillation
Damped oscillation Harmonic
Harmonic Damped oscilation
Damped oscilation Damped trend
Damped trend Damped frequency of oscillation formula
Damped frequency of oscillation formula Driven damped pendulum
Driven damped pendulum Natural and forced response
Natural and forced response Natural response and forced response example
Natural response and forced response example A subsequent
A subsequent Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Thang điểm glasgow
Thang điểm glasgow Chúa yêu trần thế
Chúa yêu trần thế Môn thể thao bắt đầu bằng chữ f
Môn thể thao bắt đầu bằng chữ f Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất