Respiratory Calculations Gas Laws Oxygen therapy Humidity Ventilator

Respiratory Calculations • • • Gas Laws Oxygen therapy Humidity Ventilator Management Hemodynamics

Gas Laws • Dalton’s Law • Fick’s Law of Diffusion • Boyle’s Law, Charles Law, Gay-Lussac’s Combined Gas Law • Graham’s Law • Poiseuille’s Law • Temperature Conversion (C to F and vice versa)

Oxygen Therapy • • Total Flow Tank Duration Arterial & Venous O 2 Content [C(a-v)O 2] difference Alveolar Air Equation P(A-a) O 2 Gradient Heliox flow rates

Total Flow Subtract Fi. O 2 - 20 (or 21) 100 Fi. O 2 If the Fi. O 2 Is. 40 or > Use 20 (<. 40 Use 21) 20 or 21 Subtract 100 - Fi. O 2 These 2 values Will Determine the Air: O 2 ratio Add the numbers of the ratio X flow rate = Total flow

Total Flow: Example A COPD patient is currently on a 40% aerosol face mask running at 10 LPM. Calculate the total flow. 20 100 1 40 20 (1 + 3) x 10 = 40 LPM 60 3

Tank Duration Pressure of the cylinder E cylinder: . 28 H cylinder: 3. 14 PSIG x Tank factor Flow rate The flow the O 2 Device is set at

Tank Duration: Example A patient is currently on a 4 L nasal cannula. The patient needs to be transported using an E cylinder. The E cylinder reads 2200 psig on the Bourdon gauge. According to hospital policy, the tank should not be used once the pressure reading reaches 200 psig. Calculate how long the tank will last (2200 -200) x. 28 4 152. 6 minutes 60 min/hr 2. 54 Hours

Arterial & Venous O 2 Content Arterial and venous. O 2 content represents the amount of oxygen that is bound to hemoglobin and dissolved in the blood. The difference is that arterial O 2 content represents the arterial system (high O 2), and venous O 2 content represents the venous system (low O 2). Cx. O 2 = (1. 34 x Hgb x Sx. O 2) + (Px. O 2 x. 003) O 2 carried/bound to hemoglobin O 2 dissolved in blood plasma

Comparison of Ca. O 2 & Cv. O 2 Arterial O 2 Content Ca. O 2 = (1. 34 x Hgb x Sa. O 2) + (Pa. O 2 x. 003) A constant Hemoglobin Arterial Partial saturation Pressure A constant Of arterial O 2 Venous O 2 Content Cv. O 2 = (1. 34 x Hgb x Sv. O 2) + (Pv. O 2 x. 003) Partial Venous Pressure saturation Of venous O 2

Arterial O 2 Content: Example Given the following values, calculate the Ca. O 2: Pa. O 2 = 93 mm. Hg Pv. O 2 = 47 mm. Hg Sa. O 2 = 98% Sv. O 2 = 77% Hemoglobin = 16 g/d. L Ca. O 2 = (1. 34 x 16 x. 98) + (93 x. 003) Ca. O 2 = 21. 01 +. 279 = 21. 29 vol % Normal value for Ca. O 2 is approximately 20 vol %

Venous O 2 Content: Example Given the following values, calculate the Cv. O 2: Pa. O 2 = 93 mm. Hg Pv. O 2 = 47 mm. Hg Sa. O 2 = 98% Sv. O 2 = 77% Hemoglobin = 16 g/d. L Cv. O 2 = (1. 34 x 16 x. 77) + (47 x. 003) Cv. O 2 = 16. 51 +. 141 = 16. 65 vol % Normal Cv. O 2 is approximately 15 vol %

C(a-v) Difference The C(a-v) difference represents the difference between arterial And venous oxygen content. It is a reflection of oxygen Consumption (oxygen used by tissues within the body) Recall the values from the 2 previous examples: Ca. O 2 = 21. 29 vol % Cv. O 2 = 16. 65 vol % To determine the C(a-v)O 2, simply subtract: Ca. O 2 - Cv. O 2 21. 29 - 16. 65 = 4. 64 vol % Normal C(a-v)O 2 = 5 vol %

C(a-v) difference: Clinical Info C(a-v)O 2 can be an important clinical indicator. Recall that The C(a-v)O 2 reflects the amount of oxygen taken from arterial Blood to be used by body tissues. Refer to the diagram below: O 2 Arterial: Ca. O 2 = 20 vol% Arterial blood contains Approx 5 vol% of O 2 Tissues O 2 5 vol% of O 2 Is extracted from Arterial blood Venous: Cv. O 2 = 15 vol% O 2 that is NOT extracted From arterial blood enters Venous circulation

C(a-v) Difference con’t… When blood flows through the body at a normal rate, approximately 5 vol% of the O 2 present in arterial blood is extracted by the tissues. The remaining O 2 enters the venous system. When blood flows through the body slower than normal, blood begins To pool and more O 2 is taken from arterial blood. With the tissues Extracting more O 2, less O 2 is present in the venous system. If you Have a lower venous O 2 content, and subtract it from the Ca. O 2, you Get a greater C(a-v)O 2 difference An increase in the C(a-v)O 2 difference = a decrease in cardiac output

Alveolar Air Equation The Alveolar air equation represents the partial Pressure of oxygen in the alveoli A/C This is what we Are finding using The alveolar Air equation Alveolus PAO 2 O 2 O 2 diffusion Pa. O 2 O 2 O 2 Capillary M E M B R A N E

Alveolar Air Equation: Con’t… PAO 2 = [(PB-PH 2 O) Fi. O 2] - Pa. CO 2 /. 8 Barometric pressure Normal is 760 mm. Hg O 2 concentration Water pressure Constant: 47 mm. Hg Arterial CO 2 Constant: Respiratory Quotient CO 2 removed/O 2 consumed 200 m. L/ 250 m. L =. 8

Alveolar Air Equation: Example Given the following information, calculate the PAO 2 PB = 760 mm. Hg Fi. O 2 =. 60 Pa. CO 2 = 40 mm. Hg Pa. O 2 = 88 mm. Hg Hgb = 14 g/d. L PAO 2 = [(760 - 47). 60] - 40 /. 8 = 377. 8 mm. Hg

P(A-a)O 2 Gradient P(A-a)O 2 represents the difference between the partial pressure Of O 2 in the alveoli and the partial pressure of O 2 in the arteries. In other words, it reflects how much of the available O 2 (PAO 2) Is actually diffusing into the blood (Pa. O 2). In a healthy individual, the P(A-a)O 2 should be very small. In other words, the majority of the available O 2 is diffusing Into the blood (refer to the diagram on the “alveolor air Equation slide for a better understanding) If the P(A-a)O 2 increases, it signals there is some problem with the gas diffusion mechanism (shunting for example).

P(A-a)O 2 Gradient: Example Using the PAO 2 calculated earlier (377. 8 mm. Hg), calculate The P(A-a)O 2 if the Pa. O 2 is 80 mm. Hg P(A-a)O 2 = 377. 8 - 80 297. 8 mm. Hg What does this number tell you? This number indicates that a significant amount of the available O 2 is not diffusing into the blood, indicating a shunt is present

Heliox Flow Rates Heliox is a mixture of helium and oxygen. Because helium is less Dense than oxygen, it is used to carry oxygen past airway Obstructions. Because heliox is less dense than pure oxygen, It has a faster flow. 2 different heliox mixtures: Multiply flow Reading by A factor of 1. 8 To get actual flow Helium : Oxygen 80 : 20 70 : 30 Multiply flow Reading by A factor of 1. 6 to Get actual flow

Heliox Flow Rates: Example A physician orders 80: 20 heliox to be run at 18 LPM. At what flow rate should the flow meter be set? We know that Set Flow rate x 1. 8 = actual flow of 80: 20 heliox We can rearrange this equation to solve for the set flow rate: Set flow rate = Actual flow / 1. 8 Set flow rate = 18 LPM / 1. 8 Set flow rate = 10 LPM In order to have an actual flow of 18 LPM, we need to set the Flow meter at 10 LPM (If this were a 70: 30 mixture, replace 1. 8 with 1. 6)

Humidity • Body Humidity

Body Humidity Normal body humidity is expressed as 44 mg/L or 47 mm. Hg This means that at 98. 6 F (37 C) gas is saturated with 44 mg. Hg or 44 mg/L of water vapor Relative Humidity: What is the relative humidity Of a gas saturated with 30 mg/L Of water at body temperature? 30 mg/L 44 mg/L = 68% Humidity Deficit: What is the humidity deficit Of a gas saturated at 30 mg/L Of water at body temperature? 44 mg/L - 30 mg/L = 14 mg/L

Ventilator Management • • Compliance (dynamic vs. static) Resistance I-time, peak flow rate, vt I: E ratio Desired CO 2 / VE Desired Pa. O 2 VD/VT Minute Ventilation / Alveolar Ventilation

Compliance Generic Equation ∆ Volume ∆ Pressure Dynamic Static Graph of Mechanical Breath

Dynamic Compliance Tidal Volume (m. L) Peak Pressure - PEEP Dynamic compliance measures the elasticity of the lung During air movement. It is a less reliable indicator of lung Elasticity compared to static compliance Note: Peak Pressure = PIP

Static Compliance Tidal Volume (m. L) Plateau Pressure - PEEP Static compliance measures the elasticity of the lung When there is no air movement. It is the best indicator Of the ability to ventilate the lungs. Normal static compliance is: 60 - 70 m. L/cm. H 2 O Note: Plateau pressure = PPL = Static Pressure

Understanding Compliance ∆ Volume ∆ Pressure m. L cm. H 2 O Compliance tells that for every 1 cm. H 2 O pressure the lungs Can hold X m. L of air. The more m. L of air that a lung can hold Per cm. H 2 O, the more compliant the lung. Example: Patient A: 30 m. L/cm. H 2 O Patient B: 60 m. L/cm. H 2 O Patient B has more compliant lungs. Patient A’s lungs Can only hold 30 m. L of air for every cm. H 2 O of pressure, Whereas patient B can hold 60 m. L of air for every cm. H 2 O.

Compliance Example 1 Calculate the static compliance given the following Information: Fi. O 2: . 60 Peak Pressure: 38 cm. H 2 O Vt: 600 m. L Vt PPL - PEEP 600 29 - 5 Rate: 12 bpm Plateau Pressure: 29 cm. H 2 O PEEP: +5 cm. H 2 O 25 m. L/cm. H 2 O

Compliance Example 2 Calculate the static compliance given the following Information: Fi. O 2: . 60 Peak Pressure: 38 cm. H 2 O Vt: 600 m. L Vt PIP - PEEP 600 38 - 5 Rate: 12 bpm Plateau Pressure: 29 cm. H 2 O PEEP: +5 cm. H 2 O 18. 18 m. L/cm. H 2 O

Compliance Clinical Scenario Mr. J arrived to the ER in acute respiratory distress. He was Subsequently intubated and placed on mechanical ventilation In the ICU. Reviewing Mr. J’s ventilator sheet reveals the Following information: 8: 00 a. m. Plateau Pressure: 22 cm. H 2 O PEEP: 5 cm. H 2 O Tidal Volume: 600 m. L 12: 00 p. m. 27 cm. H 2 O 5 cm. H 2 O 600 m. L 4: 00 a. m. 31 cm. H 2 O 5 cm. H 2 O 600 m. L What does the information reveal about the compliance of Mr. J’s lungs?

Compliance Clinical Scenario 600 m. L 22 cm. H 2 O - 5 cm. H 2 O 27 cm. H 2 O - 5 cm. H 2 O 31 cm. H 2 O - 5 cm. H 2 O 35. 29 m. L/cm. H 2 O 27. 27 m. L/cm. H 2 O 23. 08 m. L/cm. H 2 O Compliance is decreasing --> Increasing static pressure results In a decreased compliance

Airway Resistance (Raw) Airway resistance measures the force that opposes gas flow Through the airway Normal airflow Increased Raw Normal Raw is 0. 6 - 2. 4 cm. H 2 O/L/Sec on a non-intubated Patient, and 5 cm. H 2 O/L/Sec on an intubated patient

Airway Resistance (Raw) Peak Pressure - Plateau Pressure Flow must be in L/sec. If flow is given in L/min, Divide the flow by 60 seconds before placing It in the equation Example: Convert 60 L/min to L/sec 60 L/min 60 1 L/sec

Airway Resistance Example Calculate the airway resistance, given the following Fi. O 2: . 60 Peak Pressure: 38 cm. H 2 O Vt: 600 m. L Flow: 40 LPM 60 1 st convert the flow PIP - PPL Flow Rate: 12 bpm Plateau Pressure: 29 cm. H 2 O PEEP: +5 cm. H 2 O 38 - 29. 67 L/sec 13. 43 cm. H 2 O/L/Sec

I-time, Peak flow, Vt The following generic equation can be used to find I-time, peak flow rate, and tidal volume Tidal Volume (in L) = Peak Flow(LPM) I-time 60

Finding I-time is the inspiratory portion of a breath. In other words, It is the amount of time spent on inspiration E-time I-time To find I-time 1 st: determine the length of a single breath 2 nd: Use the I: E ratio to determine the length of the I-time

I-Time Example Calculate the I-time given the following ventilator parameters Vt: 600 cc Rate: 12 bmp Peak Flow: 60 LPM I: E = 1: 2 Fi. O 2: . 60 1 st: determine the length of a single breath There are 12 breaths in 1 minute and 60 seconds in 1 minute. Therefore 60 seconds / 12 breaths = 1 breath every 5 seconds Therefore, then legnth of 1 breath is 5 seconds 2 nd: Use the I: E ratio to determine the length of the I-time 1 x + 2 x = 5 1 x equals the inspiratory portion of the 3 x = 5 Breath. 1 x 1. 67 = 1. 67 seconds X = 5/3 or 1. 67

Finding Peak Flow Find the peak flow, given the following VT = 750 cc RR = 15 I: E = 1: 2. 5 First find the I-time (see the previous slide): 1. 14 sec Tidal Volume (in L) = Peak Flow(LPM) I-time 60. 750 1. 14 (. 750)60 = 1. 14 X X 60 = 45 1. 14 39. 47 LPM

Finding Vt Find the Vt given the following: PF = 50 LPM, RR = 14, I: E = 1: 2 First, Find the I-time: 1. 43 sec Tidal Volume (in L) = Peak Flow(LPM) I-time 60 X 1. 43 (1. 43)50 = 60 X 71. 5 50 60 X = 1. 1917 L or 1191. 7 m. L

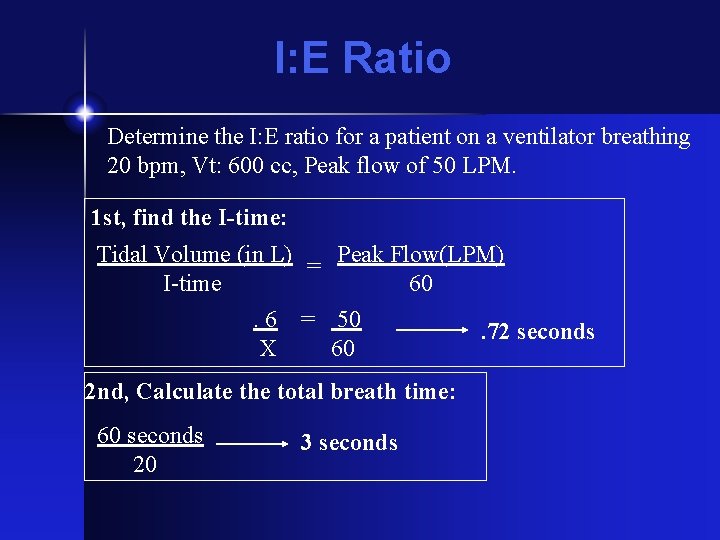
I: E Ratio Determine the I: E ratio for a patient on a ventilator breathing 20 bpm, Vt: 600 cc, Peak flow of 50 LPM. 1 st, find the I-time: Tidal Volume (in L) = Peak Flow(LPM) I-time 60. 6 = 50. 72 seconds X 60 2 nd, Calculate the total breath time: 60 seconds 20 3 seconds

I: E Ratio I-time: . 72 seconds Total breath time: 5 seconds Remember that a total breath is composed of an inspiratory Time and expiratory time, therefore: Total time - I-time = E-time 3 -. 72 = 4. 28 I-time : E-time. 72 : 2. 28 Convert to a 1: X ratio. 72 : 2. 28. 72 1 : 3. 2

Achieving correct CO 2/Minute ventilation Current VE x Current Pa. CO 2 Desired Pa. CO 2 Example: The doctor wants to decrease a patients Pa. CO 2 from 50 mm. Hg to 35 mm. Hg. The doctor wants your advice on a proper minute ventilation. The current settings include a rate of 12 and a tidal volume of 500 m. L. Current VE = 12 x 500 = 6000 m. L or 6 L 6 L x 50 35 8. 57 L You would need to se the Ventilator with a rate and tidal Volume that equals 8. 57 L. (e. g. rate of 10, Vt of 857 m. L)

Achieving correct Pa. O 2 Desired Pa. O 2 x Fi. O 2 Current Pa. O 2 Example: A patient is currently hypoxic with a Pa. O 2 Of 60 on an Fi. O 2 of. 45. The physician orders to maintain A Pa. O 2 of at least 80 mm. Hg and asks you to adjust the Ventilator accordingly 80 mm. Hg x. 45 60 mm. Hg Increase the Fi. O 2 to. 60 to achieve a Pa. O 2 Of 80 mm. Hg

VD/Vt The VD/Vt equation illustrates the % of gas that does not Participate in gas exchange. In other words, it reflects The % of gas that is deadspace. Pa. CO 2 -Pe. CO 2 Pa. CO 2 Deadspace refers to ventilation in the absence of perfusion O 2 O 2 Alveoli capillary Blocked blood flow

VD/Vt example Calculate the VD/Vt given the following: Pa. O 2: 88 mm. Hg Pa. CO 2: 40 mm. Hg Pa. CO 2 -Pe. CO 2 Pa. CO 2 40 - 31 40 Vt: 550 m. L Pe. CO 2: 31 mm. Hg To determine the actual volume Of deadspace, just multiply The % deadspace by the given Tidal volume: . 225 x 550 = 123. 75 m. L = 22. 5% Normal deadspace: 20 - 40%, up to 60% on ventilator

Minute/Alveolar Ventilation Minute ventilation refers the volume of gas inhaled during A 1 minute period. Minute ventilation(VE) = Tidal volume x Respiratory rate Normal Minute ventilation = 5 - 10 LPM Alveolar ventilation refers the volume of gas that actually Participates in gas exchange. Alveolar ventilation = (tidal volume - deadspace) x RR 1 m. L/lb of body weight Or 1/3 of tidal volume

Example Calculate the alveolar minute ventilation for a 150 lb male With a respiratory rate of 18 and tidal volume of 500 m. L Alveolar ventilation = (500 - 150) x 18 = 6300 m. L or 6. 3 L

Hemodynamics • • Shunt Pulmonary vascular resistance Systemic vascular resistance Mean pressure Pulse pressure Cardiac output (Fick's equation) Stroke Volume Cardiac Index