Resource Allocation Deadlock and Bankers Algorithm 60 330

Resource Allocation, Deadlock and Banker’s Algorithm 60 -330 Supplementary Notes Dr. R. D. Kent Last modified: Dec. 11, 2006

Introduction n These slides are intended to illustrate and clarify some details of deadlock detection and avoidance applied to resource allocation. ¡ n In particular, they clarify examples in the textbook by providing significant detail Assume that all resource types and the number of instances of each type are known by the O/S ¡ ¡ Initially configured at system startup/bootstrap Tracked along with processes as they n n Request resources for the first time Use resources dynamically

Assumed Knowledge (1) n Configured at startup and updated regularly ¡ All resource types and the number of instances of each type n n n Stored in a vector called Available with M entries (one for each resource type). Available[ j ] = k ; /* implies there are k instances of resource type j */ At a given, specific time ¡ The maximum resource demand of each of N processes n n Stored in a Nx. M matrix Max[ i ][ j ] = k ; /* process Pi may request at most k instances of resource type Rj

Assumed Knowledge (2) n At a given, specific time: ¡ The number of resources of each type currently allocated to each of N processes n n ¡ Stored in a Nx. M matrix Allocation[ i ][ j ] = k ; /* process Pi is currently allocated k instances of resource type Rj The remaining resource needs of each process n n n Stored in a Nx. M matrix Need[ i ][ j ] = k ; /* process Pi may need k instances of resource type Rj to complete its task NOTE: Need = Max – Allocation ;

Assumed Knowledge (3) n Comments: ¡ ¡ ¡ The contents of these data structures varies over time as the processes progress to completion through the states Sometimes it is convenient to refer to an entire row of an Nx. M matrix X as Xi, where Xi is a vector of length M that is associated with process Pi. Notation: Assume X, Y are vectors of length N n n X ≤ Y if and only if X[j] ≤ Y[j] for all j = 1. . N Ex. X = (1, 7, 3, 2) and Y = (0, 3, 2, 1) implies Y ≤ X

Assumed Knowledge (4) n Comments: (continued) ¡ The required vector and matrix data structures may be declared (statically) at compile time n Need to consider the maximum number of processes (large) and resources (small) that the hardware and operating system can manage. ¡ Ex. n n ¡ int Available [ MAX_Process ] ; int Max [MAX_Process ] [ MAX_Resource ] ; If structures are allocated dynamically, code must be developed to manage the heap

Banker’s Algorithm n Used to determine safe resource allocation to processes ¡ Safety implies no deadlocks will occur n n ¡ By studying different scenarios of possible resource allocation, we try to find at least one scenario that is deadlock free, or safe Time consuming (algorithm complexity) Resource allocation is performed using safe scenarios n Can a request be safely granted?

Banker’s Algorithm n At a given time assume that current values are stored in structures ¡ Define: n n ¡ NP : : Number of current processes NR : : Number of currently available resources Data Structures: n n Available – vector with NR entries Max, Allocation, Need – matrices with NP rows and NR entries in each row

Safety Algorithm n Periodically, we need to determine if the system in a safe state. ¡ Define vectors n int Work. Safe [ NR ] ; int Finish [ NP State: For a set of processes there exists at least one schedule of allocating resources so that each ¡ process can progress to completion. Initialize n n Work = Available ; For all k, Finish[ k ] = false ; /* 0 */ ];

Safety Algorithm n Goal: If all values Finish [ k ] == true (or 1), then the system is in a safe state. Starting at k = 0 (ie. first process). ¡ First step: n ¡ If both Finish[ k ] == false and Need k ≤ Work Then goto Third step, otherwise continue. Second step: n Work = Work + Allocation k ; Finish[ k ] = true ; /* or 1 */ k=k+1; if k < NR then goto First step, otherwise report “No safe state exists”.

Safety Algorithm n Third step: n If, for all k from 0 to NR-1, Finish[ k ] == true Then system is in a safe state. n Note that it is possible that no safe state exists (see Second step). ¡ Therefore there is possibility of deadlock.

Resource-Request Algorithm n We need to determine if a resource request can be safely granted. n Define an Nx. M matrix Request that contains all current resource requests (from M resource types) for all N processes. ¡ ¡ Request k is the resource request vector (a row in the matrix) for the process Pk. Resource request information (integer values) is obtained when jobs are submitted (through job headers).

Resource-Request Algorithm n When Pk requests resources: ¡ Step 1: n ¡ If Requestk ≤ Needk , goto Step 2, otherwise report “Processes exceed max. claim” Step 2: n If Requestk ≤ Available, goto Step 3, otherwise make Pk wait since resources are not available

Resource-Request Algorithm ¡ Step 3: (Prove the scenario is safe) n n n ¡ If the resulting resource-allocation scenario is safe, the allocate the resources to Pk to complete the transaction. n ¡ Available = Available - Requestk ; Allocationk = Allocationk + Requestk ; Needk = Needk – Requestk ; Requires applying the Safety Algorithm If the state is not safe, then Pk must wait for Requestk , and the old state is restored.

Example: Safe State Available [0] [1] [2] 3 3 2 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 Various processes have requested the maximum amount of resources they intend to use (Max). They are allocated resources so that, at a given moment, one knows the Allocation matrix and also what is currently Available. Max [0] [1] [2] 0 7 5 3 0 0 3 2 2 3 0 2 9 0 2 P 3 2 1 1 2 2 2 P 4 0 0 2 4 3 3 Is the system in a safe state? What is a safe sequence? Following the textbook, we assume that the maximum resources available are: (10, 5, 7)

Example Available [0] [1] [2] 3 3 2 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 Determine current Need = Max – Allocation Max [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 0 0 3 2 2 P 1 1 2 2 3 0 2 9 0 2 P 2 6 0 0 P 3 2 1 1 2 2 2 P 3 0 1 1 P 4 0 0 2 4 3 3 P 4 4 3 1

Example Available [0] [1] [2] 3 3 2 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 Determine current Need = Max – Allocation Max [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 0 0 3 2 2 P 1 1 2 2 3 0 2 9 0 2 P 2 6 0 0 P 3 2 1 1 2 2 2 P 3 0 1 1 P 4 0 0 2 4 3 3 P 4 4 3 1 Max – Allocation → Need : : 3– 2=1 2– 0=2

Example Determine all processes that can be satisfied by the Available resources. Available [0] [1] [2] 3 3 2 NOTE: Both P 1 and P 3 are candidates, but we choose P 1 because it occurs next. Allocation [0] [1] [2] Max P 0 0 1 P 1 2 P 2 [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 0 0 3 2 2 P 1 1 2 2 3 0 2 9 0 2 P 2 6 0 0 P 3 2 1 1 2 2 2 P 3 0 1 1 P 4 0 0 2 4 3 3 P 4 4 3 1

Example Available [0] [1] [2] 2 1 0 Allocation [0] [1] [2] P 0 0 1 P 1 3 Now perform the Allocation of Needed resources to P 1 Subtract Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 2 1 1 2 2 2 P 3 0 1 1 P 4 0 0 2 4 3 3 P 4 4 3 1 P 2 Add Need Max

Example Available [0] [1] [2] 2 1 0 Allocation [0] [1] [2] P 0 0 1 P 1 3 P 2 Available Max [0] [1] [2] 5 3 2 Once a process’ needs are fulfilled, free those resources to re-allocate to the next process in sequence. [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 2 1 1 2 2 2 P 3 0 1 1 P 4 0 0 2 4 3 3 P 4 4 3 1 Since the Maximum requirement is fulfilled, the process can run to completion in order to free its resources to other processes.

Example Available [0] [1] [2] 5 3 2 Reapply the updated Available to Need and arrive at the choice of P 3 (P 4 would work, but occurs later). Then, free its resources. Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 Max [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 2 1 1 2 2 2 P 3 0 1 1 P 4 0 0 2 4 3 3 P 4 4 3 1

Example Available [0] [1] [2] 5 2 1 Reapply the updated Available to Need and arrive at the choice of P 3 (P 4 would work, but occurs later). Then, free its resources. Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 Max [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 2 2 2 P 3 - - - P 4 0 0 2 4 3 3 P 4 4 3 1

Example Available [0] [1] [2] 7 4 3 Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 Reapply the updated Available to Need and arrive at the choice of P 4 (the next one that is satisfied). Max [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 - - - 2 2 2 P 3 - - - P 4 0 0 2 4 3 3 P 4 4 3 1

Example Allocate the Need resources to P 4. Available [0] [1] [2] 3 1 2 Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 Max [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 - - - 2 2 2 P 3 - - - P 4 4 3 3 P 4 - - -

Example Allocate the Need resources to P 4. Available [0] [1] [2] 7 4 5 Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 Then, since P 4 can run to completion, free its resources. Max [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 - - - 2 2 2 P 3 - - - P 4 - - - 4 3 3 P 4 - - -

Example Available [0] [1] [2] 7 4 5 Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 Both P 0 and P 2 can be satisfied from Available resources. Choose P 0 to Allocate the Need. (NOTE: the textbook chooses P 2 for this example. ) Max [0] [1] [2] Need [0] [1] [2] 0 7 5 3 P 0 7 4 3 - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 - - - 2 2 2 P 3 - - - P 4 - - - 4 3 3 P 4 - - -

Example Available [0] [1] [2] 0 0 2 Allocation [0] [1] [2] P 0 7 5 P 1 - P 2 Both P 0 and P 2 can be satisfied from Available resources. Choose P 0 to Allocate the Need. (NOTE: the textbook chooses P 2 for this example. ) Max [0] [1] [2] Need [0] [1] [2] 3 7 5 3 P 0 - - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 - - - 2 2 2 P 3 - - - P 4 - - - 4 3 3 P 4 - - -

Example Available Both P 0 and P 2 can be satisfied from Available resources. Choose P 0 to Allocate the Need. (NOTE: the textbook chooses P 2 for this example. ) [0] [1] [2] 7 5 5 Then, free the resources Allocation [0] [1] [2] Max P 0 - - P 1 - P 2 [0] [1] [2] Need [0] [1] [2] - 7 5 3 P 0 - - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 - - - 2 2 2 P 3 - - - P 4 - - - 4 3 3 P 4 - - -

Example Finally, we handle P 2 which can clearly be satisfied because, as required, Available [0] [1] [2] 7 5 5 Allocation [0] [1] [2] P 0 - - P 1 - P 2 Need ≤ Available Max [0] [1] [2] Need [0] [1] [2] - 7 5 3 P 0 - - - 3 2 2 P 1 - - - 3 0 2 9 0 2 P 2 6 0 0 P 3 - - - 2 2 2 P 3 - - - P 4 - - - 4 3 3 P 4 - - -

Example Finally, we handle P 2 which can clearly be satisfied because, as required, Available [0] [1] [2] 1 5 5 Allocation [0] [1] [2] P 0 - - P 1 - P 2 Need ≤ Available Max [0] [1] [2] Need [0] [1] [2] - 7 5 3 P 0 - - - 3 2 2 P 1 - - - 9 0 2 P 2 - - - P 3 - - - 2 2 2 P 3 - - - P 4 - - - 4 3 3 P 4 - - -

Example Available [0] [1] [2] 10 5 7 Allocation [0] [1] [2] P 0 - - P 1 - P 2 Freeing resources may have to be limited by the actual maximum resource availability (not specified for this example). Also, recall that processes request maximum resources throughout their lifetime, not those needed immediately. Max [0] [1] [2] Need [0] [1] [2] - 7 5 3 P 0 - - - 3 2 2 P 1 - - - 9 0 2 P 2 - - - P 3 - - - 2 2 2 P 3 - - - P 4 - - - 4 3 3 P 4 - - -

Example This leads to the possible resource allocation orderings: P 1, P 3, P 4, P 0, P 2 Again, this is different than discussed in the textbook (P 2 comes first, then P 0). For these sequences the vector Finish [ k ] == true for all NP=5 processes All of the stated Needs have been shown to be allocatable from the total allowed resource set Available [0] [1] [2] 10 5 7 Need [0] [1] [2] P 0 7 4 3 4 P 1 1 2 2 1 P 2 6 0 0 5 P 3 0 1 1 2 P 4 4 3 1 3 NOTE: All resources have now been reclaimed, in agreement with initial assumption.

Example: Resource Allocation We established that the state is safe. If P 1 makes a new request: Request 1 = { 1, 0, 2 } Can this request be granted safely and immediately? Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 Need [0] [1] [2] 0 7 4 3 0 0 1 2 2 3 0 2 6 0 0 P 3 2 1 1 0 1 1 P 4 0 0 2 4 3 1 Available [0] [1] [2] 3 3 2 We started with the state tables populated with safe state values.

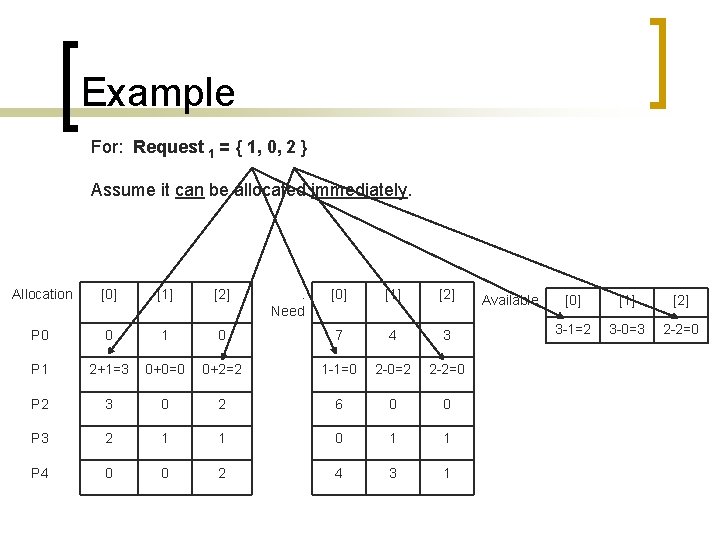
Example For: Request 1 = { 1, 0, 2 } Assume it can be allocated immediately. Allocation [0] [1] [2] P 0 0 1 P 1 2+1=3 P 2 . Need [0] [1] [2] 0 7 4 3 0+0=0 0+2=2 1 -1=0 2 -0=2 2 -2=0 3 0 2 6 0 0 P 3 2 1 1 0 1 1 P 4 0 0 2 4 3 1 Available [0] [1] [2] 3 -1=2 3 -0=3 2 -2=0

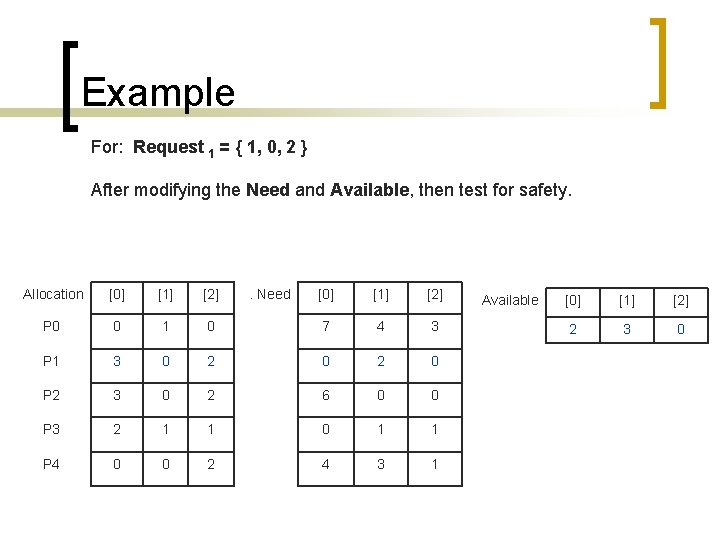
Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. Allocation [0] [1] [2] P 0 0 1 P 1 3 P 2 . Need [0] [1] [2] 0 7 4 3 0 2 0 3 0 2 6 0 0 P 3 2 1 1 0 1 1 P 4 0 0 2 4 3 1 Available [0] [1] [2] 2 3 0

Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. We find a sequence: { P 1, Allocation [0] [1] [2] P 0 0 1 P 1 3 P 2 . Need [0] [1] [2] 0 7 4 3 2 2 0 0 0 3 0 2 6 0 0 P 3 2 1 1 0 1 1 P 4 0 0 2 4 3 1 Available [0] [1] [2] 2 1 0 Allocate resources to P 1

Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. We find a sequence: { P 1, P 3, Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 . Need [0] [1] [2] 0 7 4 3 - - - 3 0 2 6 0 0 P 3 2 1 1 0 1 1 P 4 0 0 2 4 3 1 Available [0] [1] [2] 5 3 2 Free P 1 resources, Find P 3: Next <= Available

Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. We find a sequence: { P 1, P 3, Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 . Need [0] [1] [2] 0 7 4 3 - - - 3 0 2 6 0 0 P 3 2 2 2 0 0 0 P 4 0 0 2 4 3 1 Available [0] [1] [2] 5 2 1 Allocate resources to P 3

Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. We find a sequence: { P 1, P 3, P 4, Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 . Need [0] [1] [2] 0 7 4 3 - - - 3 0 2 6 0 0 P 3 - - - P 4 0 0 2 4 3 1 Available [0] [1] [2] 7 4 3 Free P 3 resources, Find P 4 (next): Next <= Available

Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. We find a sequence: { P 1, P 3, P 4, Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 . Need [0] [1] [2] 0 7 4 3 - - - 3 0 2 6 0 0 P 3 - - - P 4 4 3 3 0 0 0 Available [0] [1] [2] 3 1 2 Allocate resources to P 4

Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. We find a sequence: { P 1, P 3, P 4, P 0, Allocation [0] [1] [2] P 0 0 1 P 1 - P 2 . Need [0] [1] [2] 0 7 4 3 - - - 3 0 2 6 0 0 P 3 - - - P 4 - - - Available [0] [1] [2] 7 4 5 Free P 4 resources, Find P 0 (next): Next <= Available

Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. We find a sequence: { P 1, P 3, P 4, P 0, P 2 } Allocation [0] [1] [2] P 0 - - P 1 - P 2 . Need [0] [1] [2] - - - - - 3 0 2 6 0 0 P 3 - - - P 4 - - - Available [0] [1] [2] 7 5 5 Free P 0 resources, Find P 2 (next): Next <= Available

Example For: Request 1 = { 1, 0, 2 } After modifying the Need and Available, then test for safety. We find a sequence: { P 1, P 3, P 4, P 0, P 2 } SAFE STATE ! Allocation [0] [1] [2] P 0 - - P 1 - P 2 . Need [0] [1] [2] - - - - - 3 0 2 6 0 0 P 3 - - - P 4 - - - Available [0] [1] [2] 7 5 5 Since the state is safe, then the request R 1 can be granted immediately.

Example Having already assumed: Request 1 = { 1, 0, 2 } for P 1 Now consider, in addition: Request 4 = { 3, 3, 0 } Allocation [0] [1] [2] P 0 0 1 P 1 3 P 2 . Need [0] [1] [2] 0 7 4 3 0 2 0 3 0 2 6 0 0 P 3 2 1 1 0 1 1 P 4 0 0 2 4 3 1 for P 4. Available [0] [1] [2] 2 3 0 This request cannot be granted because there are not sufficient resources available.

Example Having already assumed: Request 1 = { 1, 0, 2 } for P 1 Next consider: Request 0 = { 0, 2, 0 } Allocation [0] [1] [2] P 0 0 1 P 1 3 P 2 . Need for P 0. [0] [1] [2] 0 7 4 3 0 2 0 3 0 2 6 0 0 P 3 2 1 1 0 1 1 P 4 0 0 2 4 3 1 It cannot be guaranteed to complete, hence it cannot free sufficient resources. Available [0] [1] [2] 2 3 0 This request cannot be granted. Although sufficient resources are available, P 0 retains a Need and this leads to an unsafe state.

Deadlock Detection n Previous Banker’s algorithms provide answers to the questions: ¡ ¡ n Is a particular system (of allocated resources) safe? Can a request for resources be granted safely? However, a safe state is not necessarily deadlock free !

Deadlock Detection n Now ask the question ¡ ¡ n For a given resource allocation state, does a deadlock exist? These slides elaborate on this point and an example This is important to support ¡ ¡ ¡ Deadlock Prevention (or Avoidance) Deadlock Recovery These slides do not discuss these points. Read the discussion in the textbook (Silberschatz, Chapter 7)

Deadlock Detection n Data structures ¡ Scalars n n ¡ Vectors n n ¡ NP : : Number of Processes NR : : Number of Resources Available, Work : : NR resources Finish : : NP processes NP x NR Matrices n n Allocation : : Each of NP processes have been allocated NR resources Request : : Each of NP processes requesting NR resources

Deadlock Detection n Algorithm ¡ Step 1: Initialize n n Work = Available ; For all k < NP ¡ ¡ if Allocation k ≠ 0 n Then Finish[ k ] = false n Else Finish[ k ] = true ; Note that Finish[k]=true; means that it cannot produce a deadlock since it does not control any resources.

Deadlock Detection n Algorithm ¡ Middle logic n Step 2: ¡ ¡ n Step 3: ¡ ¡ Find a process index k such that n Finish[ k ] == false n AND Request k ≤ Work If no k exists, goto Step 4 (Final step) Work = Work + Allocation ; Finish[ k ] = true ; Goto Step 2 This investigates every possible allocation sequence

Deadlock Detection n Algorithm ¡ Final logic n Step 4: ¡ n If Finish[ k ] == false for any k in 0 ≤ k ≤ (NR-1) n System is in a deadlock state n Else, System is deadlock free. NOTE: ¡ Finish[ k ] == false implies that Pk is deadlocked

Example: Deadlock Detection Work [0] [1] [2] (Available) 0 0 0 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 We consider the following state with declared Allocations and Available resources. A Request is made by every process at the same time. Can a sequence be found for allocating resources that does not lead to deadlock? Request [0] [1] [2] 0 0 0 2 0 2 3 0 0 0 P 3 2 1 1 1 0 0 P 4 0 0 2

Example Work [0] [1] [2] (Available) 0 0 0 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 There are two processes, P 0 and P 2, that are not requesting resources. Start at P 0 because it is first (and later, if necessary, we can try P 2 first). Request [0] [1] [2] 0 0 0 2 0 2 3 0 0 0 P 3 2 1 1 1 0 0 P 4 0 0 2

Example Assume that P 0 runs to completion, then frees its resources so they become available again. Work [0] [1] [2] (Available) 0 1 0 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 Request [0] [1] [2] 0 - - - 0 0 2 3 0 0 0 P 3 2 1 1 1 0 0 P 4 0 0 2

Example Next, P 2 is assumed to complete. Work [0] [1] [2] (Available) 0 1 0 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Request [0] [1] [2] - - 0 0 2 3 0 0 0 P 3 2 1 1 1 0 0 P 4 0 0 2

Example And, P 2 frees its resources. Work [0] [1] [2] (Available) 3 1 3 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Request [0] [1] [2] - - 0 0 2 - - - P 3 2 1 1 1 0 0 P 4 0 0 2

Example The next state (in order) that can complete is P 3. Work [0] [1] [2] (Available) 3 1 3 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 NOTE: Also could allocate and complete P 1 and P 4. Request [0] [1] [2] - - 0 0 2 - - - P 3 2 1 1 1 0 0 P 4 0 0 2

Example Allocate resources to P 3. Work [0] [1] [2] (Available) 2 1 3 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Request [0] [1] [2] - - 0 0 2 - - - P 3 3 1 1 - - - P 4 0 0 2

Example Then, reclaim resources from P 3. Work [0] [1] [2] (Available) 5 2 4 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Request [0] [1] [2] - - 0 0 2 - - - P 3 - - - P 4 0 0 2

Example Work [0] [1] [2] (Available) 5 2 4 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Noting that we can allocate resources and complete both P 1 and P 4, we choose P 4 because it is next in order. Request [0] [1] [2] - - 0 0 2 - - - P 3 - - - P 4 0 0 2

Example Allocate resources to P 4. Work [0] [1] [2] (Available) 5 2 2 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Request [0] [1] [2] - - 0 0 2 - - - P 3 - - - P 4 0 0 4 - - -

Example Then reclaim resources from P 4. Work [0] [1] [2] (Available) 5 2 6 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Request [0] [1] [2] - - 0 0 2 - - - P 3 - - - P 4 - - -

Example Finally, allocate resources to P 1. Work [0] [1] [2] (Available) 3 2 4 Allocation [0] [1] [2] P 0 - - P 1 4 P 2 Request [0] [1] [2] - - 0 2 - - - - - P 3 - - - P 4 - - -

Example And reclaim the resources from P 1. Work [0] [1] [2] (Available) 7 2 6 Allocation [0] [1] [2] P 0 - - P 1 - P 2 Request [0] [1] [2] - - - - P 3 - - - P 4 - - -

Example And reclaim the resources from P 1. Work [0] [1] [2] (Available) 7 2 6 Allocation [0] [1] [2] P 0 - - P 1 - P 2 Thus the sequence { P 0, P 2, P 3, P 4, P 1 } is deadlock free, since Finish[k] = true for all k. Request [0] [1] [2] - - - - P 3 - - - P 4 - - -

Example And reclaim the resources from P 1. Work (Available) [0] [1] [2] 0 0 0 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 Thus the sequence { P 0, P 2, P 3, P 4, P 1 } is deadlock free, since Finish[k] = true for all k. Request [0] [1] [2] 0 0 0 2 0 2 3 0 0 0 P 3 2 1 1 1 0 0 P 4 0 0 2 Other sequences that are deadlock free are: { P 0, P 2, P 3, P 1, P 4 } { P 2, P 0, P 3, P 4, P 1 }

Example: Modified request Work [0] [1] [2] (Available) 0 0 0 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 Now, modify the resource request for P 2 – it requests one more resource of type [2]. Request [0] [1] [2] 0 0 0 2 0 2 3 0 0 1 P 3 2 1 1 1 0 0 P 4 0 0 2 This request will lead to deadlock. Follow the trace as the scenario develops. . .

Example: Modified request Only P 0 has Request 0 ≤ Work [0] [1] [2] (Available) 0 0 0 Allocation [0] [1] [2] P 0 0 1 P 1 2 P 2 Request [0] [1] [2] 0 0 0 2 0 2 3 0 0 1 P 3 2 1 1 1 0 0 P 4 0 0 2

Example: Modified request Allocate resources to P 0, then reclaim. Work [0] [1] [2] (Available) 0 1 0 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Request [0] [1] [2] - - 0 0 2 3 0 0 1 P 3 2 1 1 1 0 0 P 4 0 0 2

Example: Modified request Work [0] [1] [2] (Available) 0 1 0 Allocation [0] [1] [2] P 0 - - P 1 2 P 2 Now we see that there are not sufficient resources to allocate to any other process. Request [0] [1] [2] - - 0 0 2 3 0 0 1 P 3 2 1 1 1 0 0 P 4 0 0 2 Hence, this state is deadlocked and the resource request cannot be made.

Deadlock Recovery n Read Section 7. 7 in the textbook. n Most systems take the simplest approach, aborting all deadlocked processes n More sophisticated approaches can be developed ¡ They take much more time to execute n ¡ hence are applied less often They are strongly dependent on choice of policies.

Summary n We covered essential aspects of deadlock detection and avoidance in respect of resource allocation to handle process requests. n We paid special attention to ¡ ¡ n Issue of safe states Resource allocation Read Chapter 7 of Silberschatz et al.