Resolving Conflicting Results Arising from a Pharmacometric and










- Slides: 17

Resolving Conflicting Results Arising from a Pharmacometric and a Statistical Analysis of the Cognitive Effects of a Selective Estrogen Receptor Beta Agonist (LY 500307) in Schizophrenic Patients Sihang Liu Ph. D. Candidate University at Buffalo School of Pharmacy and Pharmaceutical Sciences

Background of the Clinical Trial • A phase 1 b/2 a adaptive clinical trial of a selective estrogen beta receptor (ER-β) agonist for its preliminary effects in cognitive function in schizophrenia. • 8 -week randomized, double-blind, placebo-controlled, dose ranging, parallel group study. • Ninety-four patients were randomized across the four treatment arms: • • placebo N=29 25 mg/day N=10 75 mg/day N=29 150 mg/day N=26. • Patient Evaluations: • • MATRICS Consensus Cognitive Battery (MCCB) Fronto-parietal functional activation during N-back performance (N-back) Personal and Social Performance Scale (PSP) Adjusted Score etc.

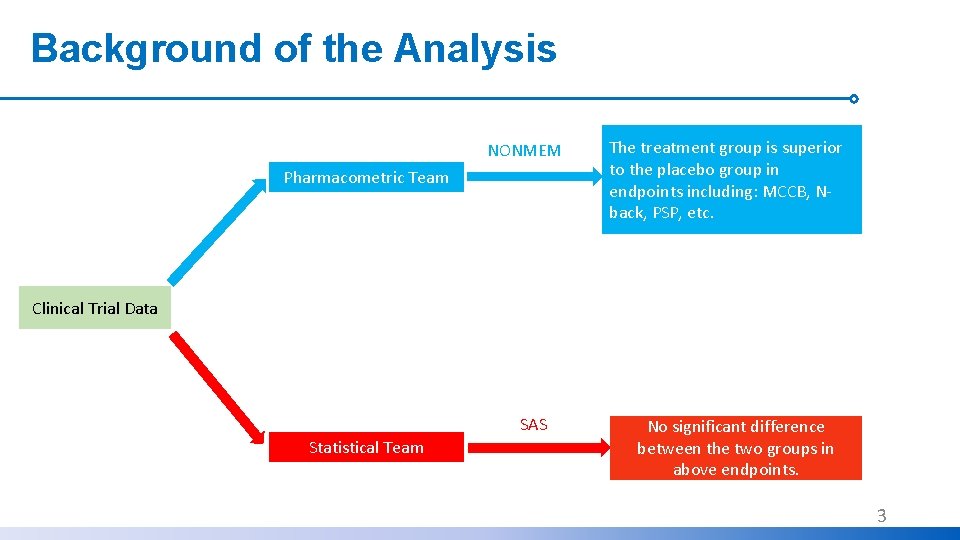
Background of the Analysis NONMEM Pharmacometric Team The treatment group is superior to the placebo group in endpoints including: MCCB, Nback, PSP, etc. Clinical Trial Data SAS Statistical Team No significant difference between the two groups in above endpoints. 3

The MATRICS Consensus Cognitive Battery (MCCB) • Widely used in international trials examining cognitive function in patients with schizophrenia (Nuechterlein et al. , 2008). • The test consists of: • • Speed of processing Attention/vigilance Working memory Verbal memory Visual learning Reasoning and problem solving Social cognition • MCCB overall composite T-score ranges from 0 to 81, where a higher score indicates a better cognitive function. • MCCB was assessed at week 0, 4, and 8. Nuechterlein, K. H. et al. (2008). The MATRICS Consensus Cognitive Battery, Part 1: Test selection, reliability, and validity. American Journal of Psychiatry, 165(2), 203 -213. Kern, R. S. et al. (2008). The MATRICS Consensus Cognitive Battery, Part 2: Co-norming and standardization. American Journal of Psychiatry, 165(2), 214 -220. 4

Initial Model Strategy Proposed by the Pharmacometric Team • Full model • Equivalent Statistical expression of the full model • Backward elimination and likelihood ratio test • Removal of the treatment slope, OFV 61. 2 (p<0. 0001, df=2) points. • Removal of the placebo slope, OFV 24. 5 (p<0. 0001, df=2) points. • Model predicted MCCB composite score change at the 8 -week endpoint • 20% increase in the treatment group • 16% increase in the placebo group 5

Initial Model Proposed by the Statistical Team • Estimates Label Estimate Standard Error DF slope for placebo 0. 07976 0. 01653 165 4. 83 <. 0001 slope for treatment 0. 09852 0. 01176 165 8. 38 <. 0001 slope for treatment - slope for placebo 0. 01876 0. 02010 165 0. 93 0. 3519 t Value Pr > |t| 6

Second Model Proposed by the Statistical Team • Result: Estimates • Label Estimate Standard Error DF t Value Pr > |t| slope for placebo 0. 08000 0. 01746 82 4. 58 <. 0001 slope for treatment 0. 09872 0. 01241 82 7. 95 <. 0001 slope for treatment - slope for placebo 0. 01873 0. 02127 82 0. 88 0. 3811 The slope for treatment is not significantly different from the slope for placebo 7

Investigating the Difference • 8

Modified backward elimination Full model: Unique Treatment Slope and Placebo Slope Remove treatment effect OFV 2. 4 (p=0. 3, df=2) points Reduced Model 1: Shared Slope Between Treatment and Placebo Remove shared slope OFV 73. 4 (p<0. 0001, df=2) points Reduced Model 2: Baseline Only 9

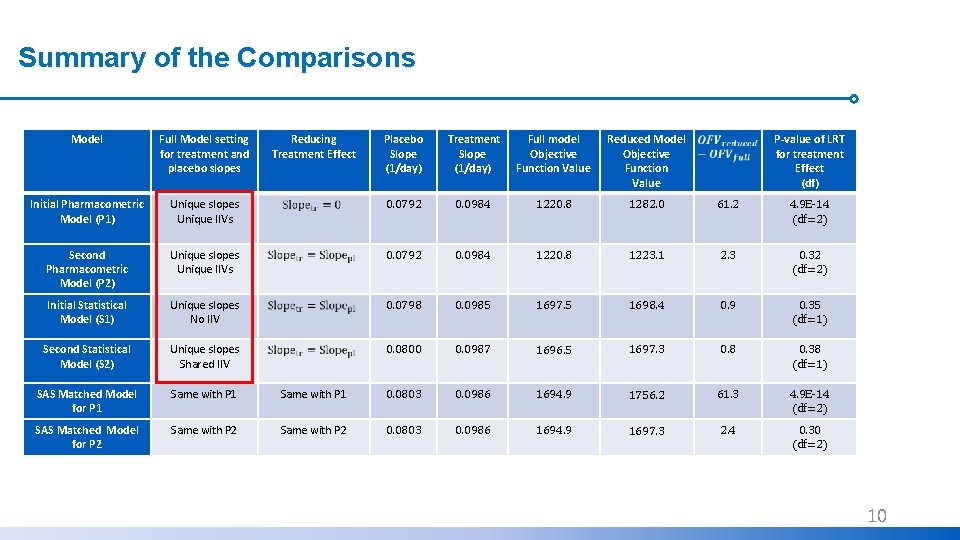
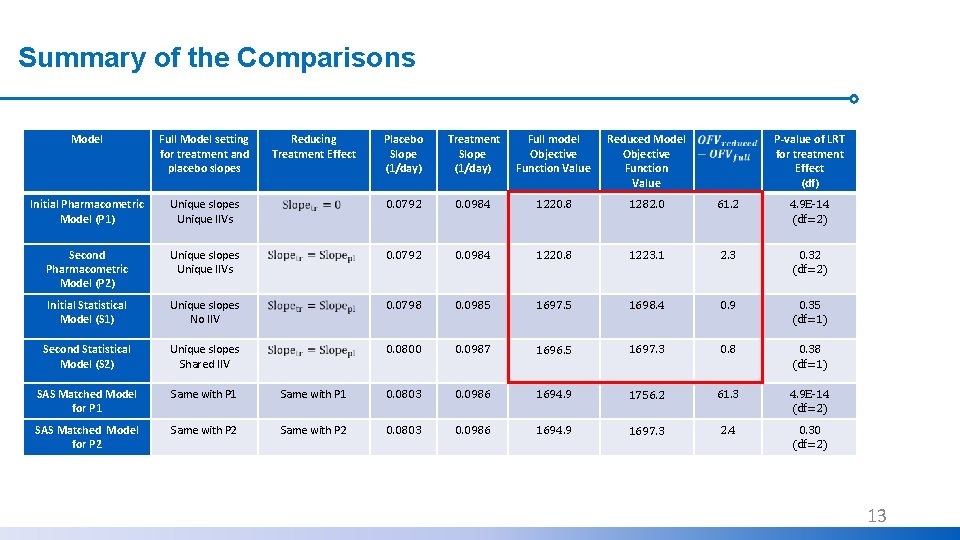
Summary of the Comparisons Model Full Model setting for treatment and placebo slopes Initial Pharmacometric Model (P 1) Reducing Treatment Effect Placebo Slope (1/day) Treatment Slope (1/day) Full model Objective Function Value Reduced Model Objective Function Value P-value of LRT for treatment Effect (df) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1282. 0 61. 2 4. 9 E-14 (df=2) Second Pharmacometric Model (P 2) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1223. 1 2. 3 0. 32 (df=2) Initial Statistical Model (S 1) Unique slopes No IIV 0. 0798 0. 0985 1697. 5 1698. 4 0. 9 0. 35 (df=1) Second Statistical Model (S 2) Unique slopes Shared IIV 0. 0800 0. 0987 1696. 5 1697. 3 0. 8 0. 38 (df=1) SAS Matched Model for P 1 Same with P 1 0. 0803 0. 0986 1694. 9 1756. 2 61. 3 4. 9 E-14 (df=2) SAS Matched Model for P 2 Same with P 2 0. 0803 0. 0986 1694. 9 1697. 3 2. 4 0. 30 (df=2) 10

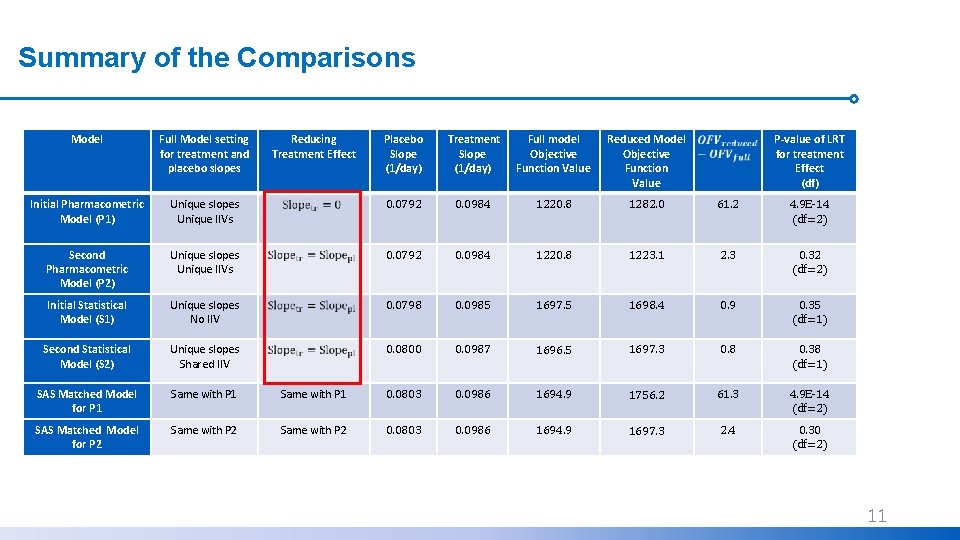
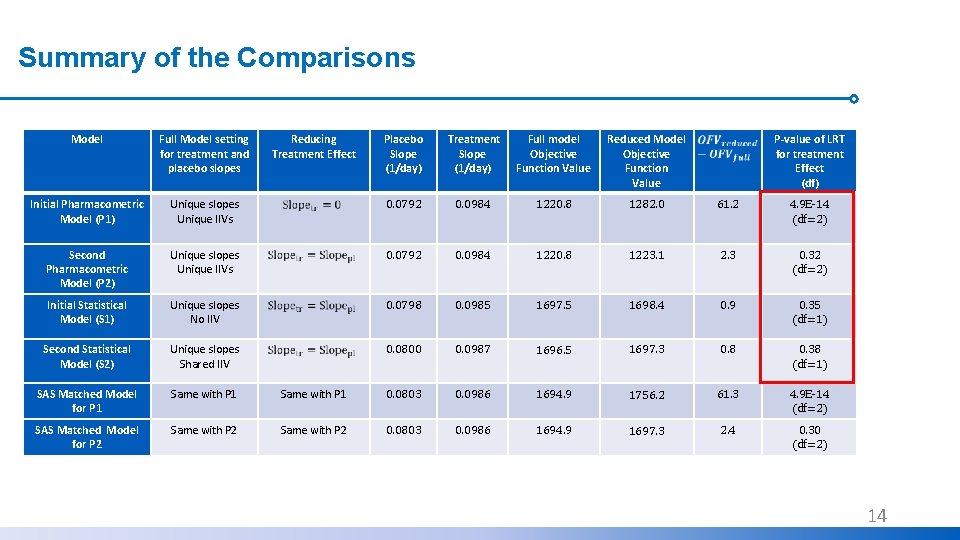
Summary of the Comparisons Model Full Model setting for treatment and placebo slopes Initial Pharmacometric Model (P 1) Reducing Treatment Effect Placebo Slope (1/day) Treatment Slope (1/day) Full model Objective Function Value Reduced Model Objective Function Value P-value of LRT for treatment Effect (df) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1282. 0 61. 2 4. 9 E-14 (df=2) Second Pharmacometric Model (P 2) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1223. 1 2. 3 0. 32 (df=2) Initial Statistical Model (S 1) Unique slopes No IIV 0. 0798 0. 0985 1697. 5 1698. 4 0. 9 0. 35 (df=1) Second Statistical Model (S 2) Unique slopes Shared IIV 0. 0800 0. 0987 1696. 5 1697. 3 0. 8 0. 38 (df=1) SAS Matched Model for P 1 Same with P 1 0. 0803 0. 0986 1694. 9 1756. 2 61. 3 4. 9 E-14 (df=2) SAS Matched Model for P 2 Same with P 2 0. 0803 0. 0986 1694. 9 1697. 3 2. 4 0. 30 (df=2) 11

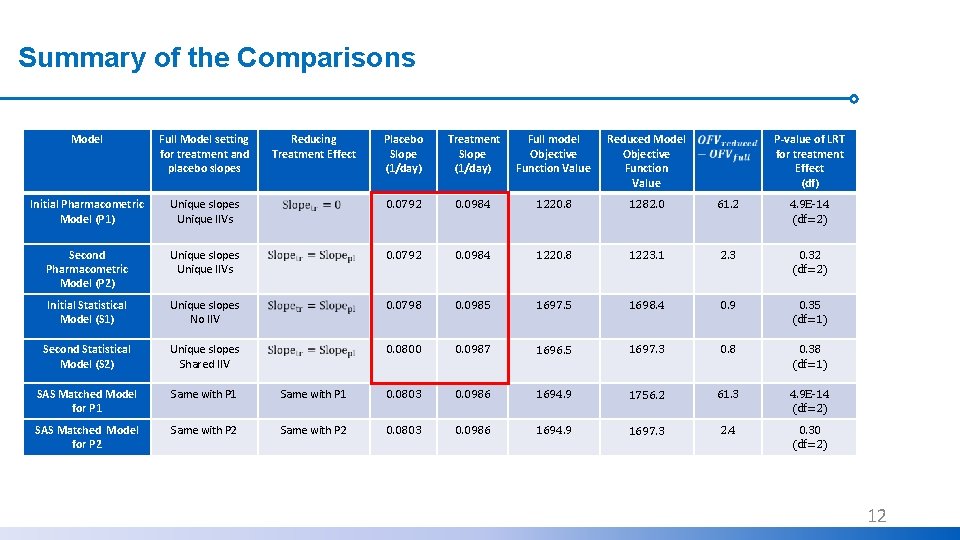
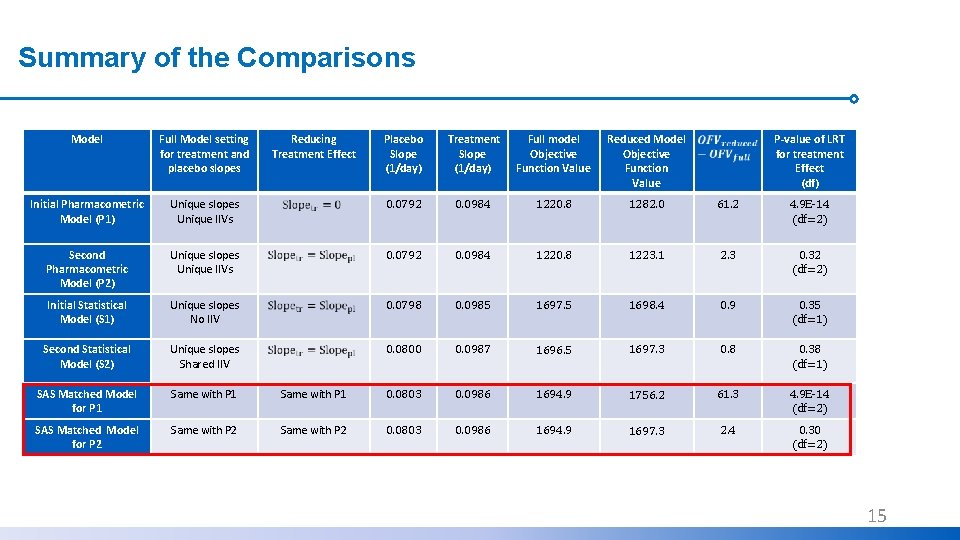
Summary of the Comparisons Model Full Model setting for treatment and placebo slopes Initial Pharmacometric Model (P 1) Reducing Treatment Effect Placebo Slope (1/day) Treatment Slope (1/day) Full model Objective Function Value Reduced Model Objective Function Value P-value of LRT for treatment Effect (df) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1282. 0 61. 2 4. 9 E-14 (df=2) Second Pharmacometric Model (P 2) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1223. 1 2. 3 0. 32 (df=2) Initial Statistical Model (S 1) Unique slopes No IIV 0. 0798 0. 0985 1697. 5 1698. 4 0. 9 0. 35 (df=1) Second Statistical Model (S 2) Unique slopes Shared IIV 0. 0800 0. 0987 1696. 5 1697. 3 0. 8 0. 38 (df=1) SAS Matched Model for P 1 Same with P 1 0. 0803 0. 0986 1694. 9 1756. 2 61. 3 4. 9 E-14 (df=2) SAS Matched Model for P 2 Same with P 2 0. 0803 0. 0986 1694. 9 1697. 3 2. 4 0. 30 (df=2) 12

Summary of the Comparisons Model Full Model setting for treatment and placebo slopes Initial Pharmacometric Model (P 1) Reducing Treatment Effect Placebo Slope (1/day) Treatment Slope (1/day) Full model Objective Function Value Reduced Model Objective Function Value P-value of LRT for treatment Effect (df) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1282. 0 61. 2 4. 9 E-14 (df=2) Second Pharmacometric Model (P 2) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1223. 1 2. 3 0. 32 (df=2) Initial Statistical Model (S 1) Unique slopes No IIV 0. 0798 0. 0985 1697. 5 1698. 4 0. 9 0. 35 (df=1) Second Statistical Model (S 2) Unique slopes Shared IIV 0. 0800 0. 0987 1696. 5 1697. 3 0. 8 0. 38 (df=1) SAS Matched Model for P 1 Same with P 1 0. 0803 0. 0986 1694. 9 1756. 2 61. 3 4. 9 E-14 (df=2) SAS Matched Model for P 2 Same with P 2 0. 0803 0. 0986 1694. 9 1697. 3 2. 4 0. 30 (df=2) 13

Summary of the Comparisons Model Full Model setting for treatment and placebo slopes Initial Pharmacometric Model (P 1) Reducing Treatment Effect Placebo Slope (1/day) Treatment Slope (1/day) Full model Objective Function Value Reduced Model Objective Function Value P-value of LRT for treatment Effect (df) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1282. 0 61. 2 4. 9 E-14 (df=2) Second Pharmacometric Model (P 2) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1223. 1 2. 3 0. 32 (df=2) Initial Statistical Model (S 1) Unique slopes No IIV 0. 0798 0. 0985 1697. 5 1698. 4 0. 9 0. 35 (df=1) Second Statistical Model (S 2) Unique slopes Shared IIV 0. 0800 0. 0987 1696. 5 1697. 3 0. 8 0. 38 (df=1) SAS Matched Model for P 1 Same with P 1 0. 0803 0. 0986 1694. 9 1756. 2 61. 3 4. 9 E-14 (df=2) SAS Matched Model for P 2 Same with P 2 0. 0803 0. 0986 1694. 9 1697. 3 2. 4 0. 30 (df=2) 14

Summary of the Comparisons Model Full Model setting for treatment and placebo slopes Initial Pharmacometric Model (P 1) Reducing Treatment Effect Placebo Slope (1/day) Treatment Slope (1/day) Full model Objective Function Value Reduced Model Objective Function Value P-value of LRT for treatment Effect (df) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1282. 0 61. 2 4. 9 E-14 (df=2) Second Pharmacometric Model (P 2) Unique slopes Unique IIVs 0. 0792 0. 0984 1220. 8 1223. 1 2. 3 0. 32 (df=2) Initial Statistical Model (S 1) Unique slopes No IIV 0. 0798 0. 0985 1697. 5 1698. 4 0. 9 0. 35 (df=1) Second Statistical Model (S 2) Unique slopes Shared IIV 0. 0800 0. 0987 1696. 5 1697. 3 0. 8 0. 38 (df=1) SAS Matched Model for P 1 Same with P 1 0. 0803 0. 0986 1694. 9 1756. 2 61. 3 4. 9 E-14 (df=2) SAS Matched Model for P 2 Same with P 2 0. 0803 0. 0986 1694. 9 1697. 3 2. 4 0. 30 (df=2) 15

Communications • This work illustrates the importance of communicating the model structures and assumptions being evaluated. • Understanding exactly what the other side is doing is the fundamental step in resolving conflicting analytical results. • Detailed communication on multiple levels including terms, parameters, model structures, model estimation method, construction of test statistics, etc. is critical to fully understand the similarities and differences between the two approaches. • The comprehensive comparison and communication facilitated learning and comprehension for pharmacometricians and statisticians. 16

Acknowledgement • • • Dr. Robert Bies, UB Dr. Alan Breier, IU Dr. Michael Francis, IU Ziheng Cheng, UB Ziyi Yang, IU 17