RescorlaWagner Model Extinction Latent Inhibition Rescorla Wagner Model

Rescorla-Wagner Model Extinction Latent Inhibition

Rescorla – Wagner Model (simplified version) DV = K(l – Vsum) l = Amount of Possible Conditioning (Associative Strength) = UCS K = Salience of stimuli (only focus on CS here) DV = Amount of Conditioning on the Current Trial to a specific CS Vsum = Sum of Prior Conditioning to All Stimuli

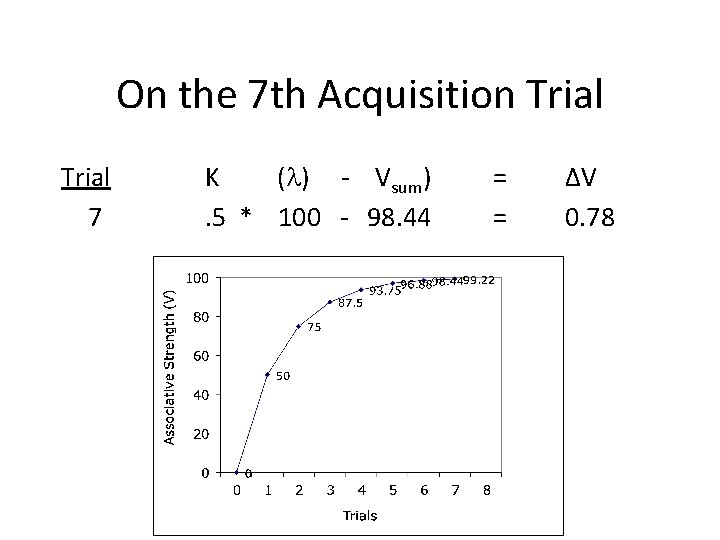
On the 7 th Acquisition Trial 7 K (l) - Vsum). 5 * 100 - 98. 44 = = ∆V 0. 78

How to model Extinction? 1. Extinction Procedure: CS -> No UCS. 2. If no UCS then l = 0 in R-W equation. 3. Basic equation will be DV = K(0 – Vsum) 4. Basic equation will produce negative value. 5. Negative value of DV is “added” to Vsum 6. Result is Vsum is reduced by that amount on next trial.

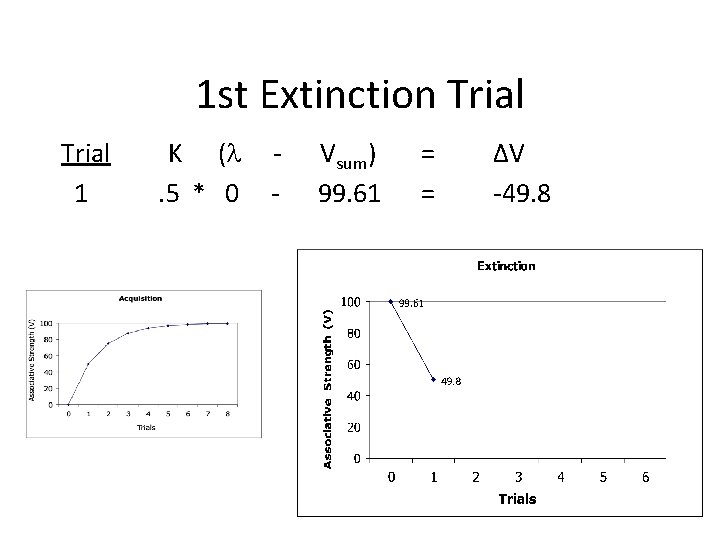
1 st Extinction Trial 1 K (l. 5 * 0 - Vsum) 99. 61 = = ∆V -49. 8

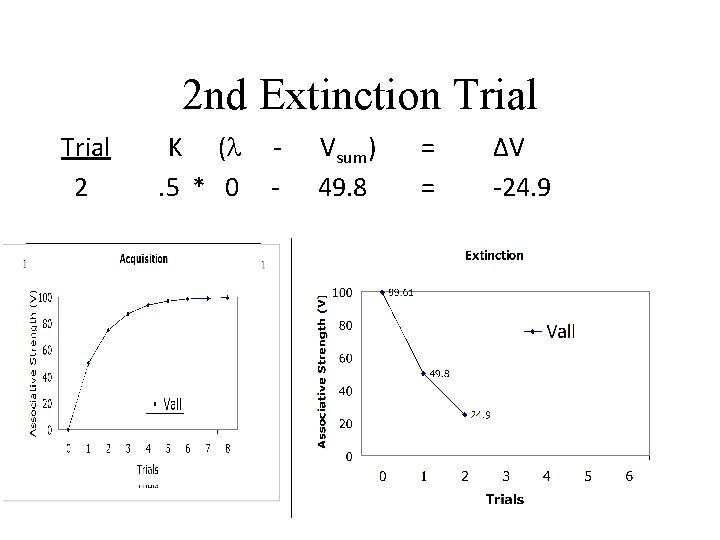
2 nd Extinction Trial 2 K (l. 5 * 0 - Vsum) 49. 8 = = ∆V -24. 9

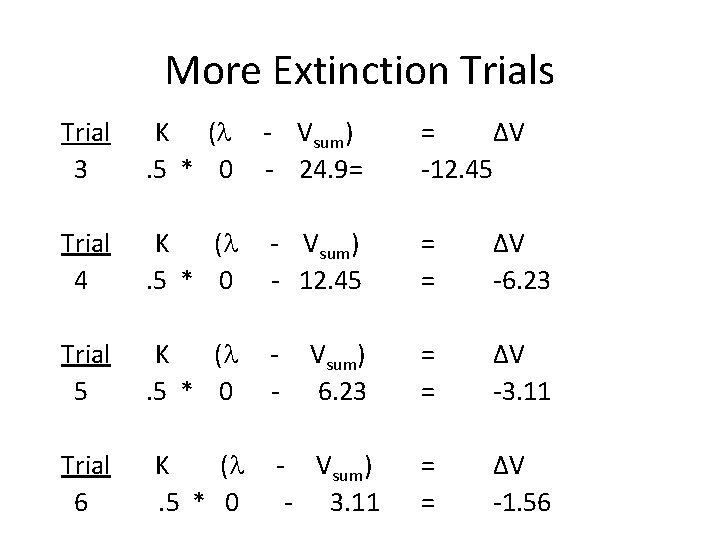
More Extinction Trials Trial 3 K (l. 5 * 0 - Vsum) - 24. 9= = ∆V -12. 45 Trial 4 K (l. 5 * 0 - Vsum) - 12. 45 = = ∆V -6. 23 Trial 5 K (l. 5 * 0 - = = ∆V -3. 11 Trial 6 K (l. 5 * 0 = = ∆V -1. 56 Vsum) 6. 23 - Vsum) - 3. 11

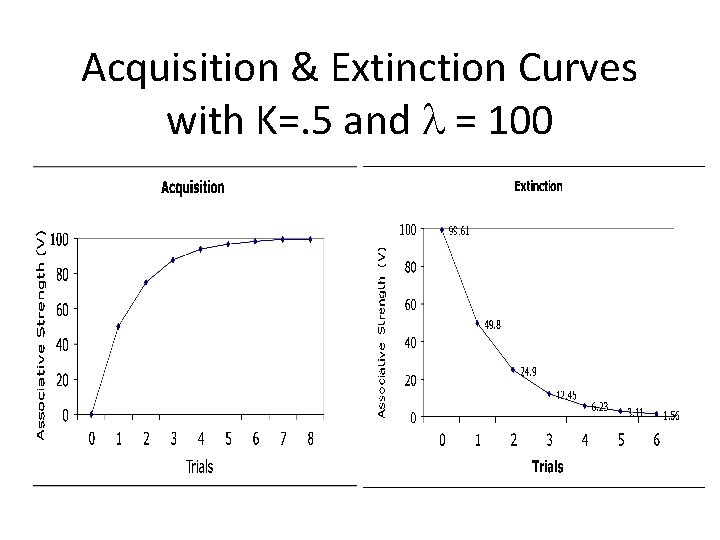
Acquisition & Extinction Curves with K=. 5 and l = 100

Rescorla-Wagner Model Problems with Extinction Basic Problem R-W explains Extinction as “Unlearning” 1. Rapid Reacquisition 2. Spontaneous Recovery

The Problem of “Latent Inhibition” (“CS preexposure effect”) Assume values for R-W model: CS (K =. 4) UCS (l = 100) Phase 1: CS presented alone, no UCS for several trials DV = K(l – Vsum) DV =. 4(0 – 0) = 0 R-W prediction is no learning Phase 2: CS UCS DV = K(l – Vsum) DV =. 4(100 – 0) R-W prediction is ordinary conditioning will begin. But actual result is inhibitory conditioning from Phase 1!