Rescorla Wagner Model Classical Conditioning and prediction Theories

Rescorla Wagner Model Classical Conditioning and prediction

Theories of Classical Conditioning: WHY do organisms respond to predictability? • Ruled out • Pavlov: Stimulus substitutability theory • Perceptual Gating Theory • Kamin: Surprise theory: • Right, but wrong • Provided some really puzzling results • Rescorla and Wagner: Computational Model • Current Attentional Models

Kamin’s work: 1967 -1974 Blocking and overshadowing • Overshadowing: • • Use one "weak" and one "strong" CS CS 1+CS 2 US Reaction to weaker stimulus is blotted out by stronger CS Demonstrated by Pavlov • CS(strong)+ CS (weak) US(shock) UR(avoidance) CR is STRONGEST • CS(strong) US(shock) UR(avoidance) CR is STRONG • CS(strong) US(shock) UR(avoidance) CR is WEAK CR (avoidance) CR (avoidance

Kamin’s work: 1967 -1974 Blocking and overshadowing • Blocking: • Train 1 CS, then add a second CS to it: • CS 1(light) US(shock) UR(avoidance) CR(avoidance) • CS 1(light)+CS 2(tone) US(shock) UR (avoidance) CR (avoidance) • Test each individually after training • CS 1(light) US(shock) UR(avoidance) CR(avoidance) • CS 2(tone) US(shock) UR(avoidance) CR(NO avoidance) • Find that only one supports a CR • One stimulus “blocks” learning to second CS • Demonstrated by Kamin

The Rescorla Wagner Equation!: • Yields an equation: THE Rescorla Wagner (1974) model!!!!! ΔV=k( λ-V 0 or Vi =αißj(λj-Vsum) • Vi = amount learned (conditioned) on a given trial • Αi = the salience of the CS • ßj = the salience of the US • (λj-Vsum) = total amount of conditioning that can occur to a particular CS-US pairing

The Rescorla Wagner Equation!: • Yields an equation: THE Rescorla Wagner (1974) model!!!!! Vi =αißj(Λj-Vsum) • What does this equation say? • The amount of conditioning that will occur on a given trial is a function of: • The size of the salience of the CS multiplied by • The size of the salience of the US multiplied by • (The maximum amount of learning) - (the amount of learning that has already occurred).

Can say this easier! • How much you will learn on a given trial (Vi) is a function of: • αi or how good a stimulus the CS is (how well it grabs your attention) • ßj or how good a stimulus the US is (how well it grabs your attention • λj or how much can learning can be learned about the CSUS relationship • AND Vsum or how much you have learned ALREADY!

Assumptions of Rescorla-Wagner (1974) model • Model developed to accurately predict and map learning as it occurs trial by trial • Assumes a bunch of givens: • Assume animal can perceive CS and US, and can exhibit UR and CR • Helpful for the animal to know 2 things about conditioning: • what TYPE of event is coming • the SIZE of the upcoming event • Thus, classical conditioning is really learning about: • signals (CS's) which are PREDICTORS for • important events (US's)

Assumptions of R-W model • Assumes that with each CS-US pairing 1 of 3 things can happen: • The CS might become more INHIBITORY • The CS might become more EXCITATORY • There is no change in the CS • How do these 3 rules work? • If US is larger than expected: CS = excitatory • If US is smaller than expected: CS= inhibitory • If US = expectations: No change in CS • The effect of reinforcers or nonreinforcers on the change of associative strength depends upon: • The existing associative strength of THAT CS • AND on the associative strength of other stimuli concurrently present

More assumptions • Explanation of how an animal anticipates what type of CS is coming: • Direct link is assumed between "CS center" and "US center": • E. g. between a tone center and food center • In 1970’s: other researchers thought R and W were crazy with this idea • Now: neuroscience shows formation of neural circuits! • Assumes that STRENGTH of an event is given • The conditioning situation is predicted by the strength of the learned connection • THUS: when learning is complete: • The strength of the association relates directly to the size or intensity of the CS • Asymptote of learning = max learning that can occur to that size or intensity of a CS • Maximum amount of learning that a given CS can support

More assumptions • The change in associative strength of a CS as the result of any given trial can be predicted from the composite strength resulting from all stimuli presented on that trial: • Composite strength = summation of conditioning that occurs to all stimuli present during a conditioning trial • If composite strength is LOW: • the ability of reinforcer to produce increments in the strength of component stimuli is HIGH • More can be learned for this trial • If the composite strength is HIGH: • reinforcement is relatively less effective (LOW) • Less can be learned for this trial- approaching max of learning

More assumptions: • Can expand to extinction, or nonreinforced trials: • If composite associative strength of a stimulus compound is high, then the degree to which a nonreinforced presentation will produce a decrease in associative strength of the components is LARGE • If composite associative strength is low- nonreinforcement effects reduced

WHY is this equation important? • We can use three rules to make predictions about amount and direction of classical conditioning • λ j > Vsum = Excitatory Conditioning • The degree to which the CS predicted the size of the US was GREATER than expected, so you react MORE to the CS next trial • λ j < Vsum = Inhibitory Conditioning • The degree to which the CS predicted the size of the US was LESS than expected, so you react LESS to the CS next trial • λ j = Vsum = no change: • The CS predicted the size of the US exactly as you expected

The Equation: Let’s USE it to Explain Learning, Overshadowing and Blocking!: Vi =αißj(Λj-Vsum) • Vi = amount learned (conditioned) on a given trial • Αi = the salience of the CS • ßj = the salience of the US • (λj-Vsum) = total amount of conditioning that can occur to a particular CS-US pairing

Okay, you got all that? Let’s put this baby to work……. we will try a few examples

The equation: Vi =αißj(λ j-Vsum) • Vi = change in associative strength that occurs for any CS, i, on a single trial • αi = stimulus salience (assumes that different stimuli may acquire associative strength at different rates, despite equal reinforcement) • ßj = learning rate parameters associated with the US (assumes that different beta values may depend upon the particular US employed) • Vsum = associative strength of the sum of the CS's (strength of CS-US pairing) • λ j= associative strength that some CS, i, can support at asymptote • In English: How much you learn on a given trial is a function of the value of the stimulus x value of the reinforcer x (the absolute amount you can learn minus the amount you have already learned).

Acquisition • FIrst conditioning trial: Assume (our givens) • CS = light; US= 1 ma Shock • Vsum = Vl; no trials so Vl = 0 • Thus: λ j-Vsum = 100 -0 = 100 • First trial must be EXCITATORY • BUT: must consider the salience of the light: • αi = 1. 0 • ßj = 0. 5

Acquisition • Plug into the equation: • for TRIAL 1 • VL 1 = (1. 0)(0. )(100 -0) = 0. 5(100) = • 50 • thus: VL 1 only approaches 50% of the discrepancy between λj and Vsum is learned for the first trial

Acquisition • TRIAL 2: • Same assumptions! • VL 2 = (1. 0)(0. 5)(100 -50) = 0. 5(50) = • 25 • Vsum = (50+25) = • 75

Acquisition • TRIAL 3: • VL 3 = (1. 0)(0. 5)(100 -75) = 0. 5(25)= • 12. 5 • Vsum = (50+25+12. 5) = • 87. 5

Acquisition • TRIAL 4: • VL = (1. 0)(0. 5)(100 -87. 5) = 0. 5(12. 5) = • 6. 25 • Vsum = (50+25+12. 5+6. 25) = • 93. 75 • TRIAL 10: Vsum = 99. 81, etc. , until reach ~100 on approx. trial 14 • When will you reach asymptote?

Now: Back to Explaining Blocking and Overshadowing • Overshadowing: • use one "weak" and one "strong" CS • reaction to weaker stimulus: less CR • Reaction to stronger stimulus: more CR • Blocking: 1 st CS blocks learning to 2 nd CS • At issue: What is predicting what? • Does LT give any more information/predictability than L alone? • If not, then L “blocks” learning to LT

How to explain overshadowing? Yep, it is good old Rescorla-Wagner to the rescue!

Remember Overshadowing • Pavlov: Compound CS • with 1 intense CS, 1 weak CS • after a number of trials found: strong CS elicits strong CR • Weak CS elicits weak or no CR • Note: BOTH CSs are presented at same time • Why would one over shadow or overpower the other? • Why did animal not attend equally to both?

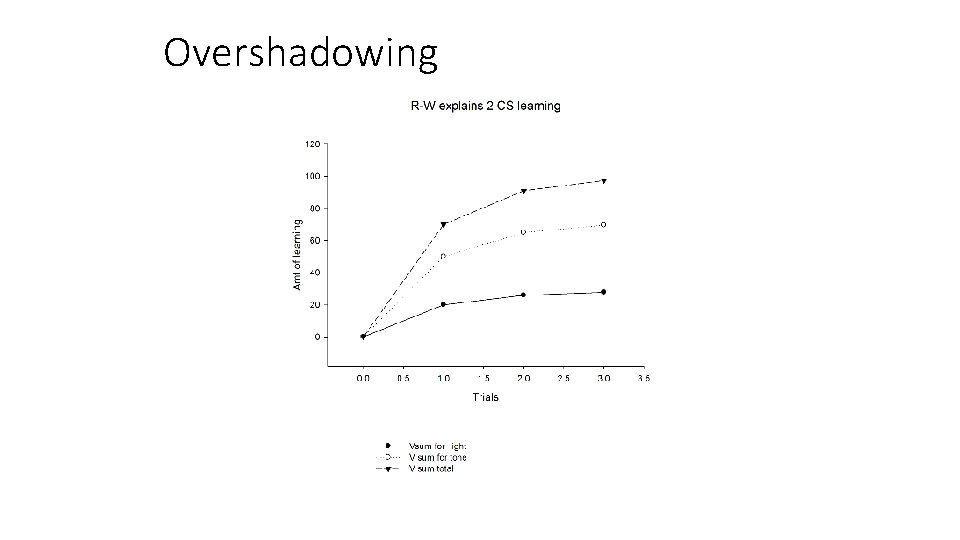
Overshadowing • Rescorla-Wagner model helps to explain why: • Assume • αL = light = 0. 2; αT = tone = 0. 5 • ßL = light = 1. 0 ; ßt = tone = 1. 0 • Plug into equation: • Vsum = Vl + Vt = 0 on trial 1 • VL = 0. 2(1)(100 -0) = • 20 • Vt = 0. 5(1)(100 -0) = • 50 • after trial 1: Vsum = • 70

Overshadowing • TRIAL 2: • VL = 0. 2(1)(100 -(50+20)) = • 6 • Vt = 0. 5(1)(100 -(50+20)) = • 15 • Vsum = (70+(6+15)) = • 91 • TRIAL 3: • VL = 0. 2(1)(100 -(91)) = • 1. 8 • Vt = 0. 5(1)(100 -(91)) = • 4. 5 • Vsum = (91+(1. 8+4. 5)) = • 97. 3 and so on • thus: reaches asymptote (by trial 6) MUCH faster w/2 CS's • NOTE: CSt takes up over 70 units of assoc. strength CSl takes up only 30 units of assoc. strength

Overshadowing

Blocking • Similar explanation to overshadowing: • Does not matter whether VL has more or less saliency than Vt , • CS has basically absorbed all the associative strength that the CS can support • Why?

Blocking • Give trials of CS A-alone to asymptote: • Reach asymptote: VL = λ j =100 =Vsum • Let’s say we did 100 trials to ensure VL is as close to asymptote as possible. • NOW add trials to compound stimuli: • CS of the light has salience: αL =. 5465 • CS of tone has salience of: ßt =0. 464 • Note that CStone has higher salience! • Eh, oh, the math is going to be TOO HARD to do!!!!!

Blocking • Or IS the math to hard to do? • First compound VLT 1 Trial: • Vt= αß(λj-Vsum) • What is Vsum for the light after training to the CS light? • That’s right Vsum = ______ • Vt=0. *1. 0*(100 -100)= _______ • No learning!

How could one eliminate blocking effect? • Increase the intensity of the US to 2 m. A with λ j now equals = 160 • Learning so far: Vsum still equals 100 (learned to 1 m. A shock) • But now: TOTAL learning is increased to 160 because we changed the US!

How could one eliminate blocking effect? • Plug into the equation: • (assume Vl and Vt equally salient) • Vt = 0. 2(1)(160 -100) = 0. 2(60) = 12 • Vl = 0. 2(1)(160 -100) = 0. 2(60) = 12 • Vsum = 100+12+12 =124

How could one eliminate blocking effect? • on trial 2: • Vsum = 124 • Vt = 0. 2(1)(160 -124) = 0. 2(36) = 7. 2 • Vl = 0. 2(1)(160 -124) = 0. 2(36) = 7. 2 • Vsum now = (124+14. 4) = 138. • Again, monotonically increasing curve. • Thus, altering the salience of the US alters the learning • Does altering the CS make the same or similar change?

The Rescorla Wagner Equation!: • Yields an equation: THE Rescorla Wagner (1974) model!!!!! Vi =αißj(Λj-Vsum) • What does this equation say? • The amount of conditioning that will occur on a given trial is a function of: • The size of the salience of the CS multiplied by • The size of the salience of the US multiplied by • (The maximum amount of learning) - (the amount of learning that has already occurred).

Can say this easier! • How much you will learn on a given trial (Vi) is a function of: • αi or how good a stimulus the CS is (how well it grabs your attention) • ßj or how good a stimulus the US is (how well it grabs your attention • λj or how much can learning can be learned about the CSUS relationship • AND Vsum or how much you have learned ALREADY!