Representing Vectors We can represent vector using a

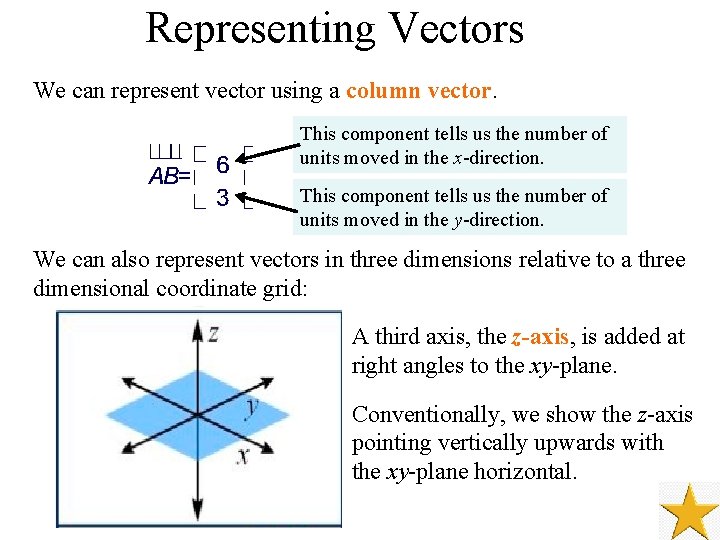
Representing Vectors We can represent vector using a column vector. This component tells us the number of units moved in the x-direction. This component tells us the number of units moved in the y-direction. We can also represent vectors in three dimensions relative to a three dimensional coordinate grid: A third axis, the z-axis, is added at right angles to the xy-plane. Conventionally, we show the z-axis pointing vertically upwards with the xy-plane horizontal.

The negative of a vector A Here is the vector a B Suppose the arrow went in the opposite direction, from B to A: A B This is the negative of the vector We can describe this new vector as: –a or

The negative of a vector In general, If then

The zero and unit vector A vector with a magnitude of 0 is called the zero vector. The zero vector is written as 0 A vector with a magnitude of 1 is called a unit vector. The most important unit vectors are those that run parallel to the xand y-axes. These are called unit base vectors. The horizontal unit base vector, The vertical unit base vector, , is called i. , is called j.

The unit base vectors, i and j, run parallel to the x- and y-axes. y-axis j x-axis i Any column vector can easily be written in terms of i and j. For example, The number of i’s tells us how many units are moved horizontally, and the number of j’s tells us how many units are moved vertically. Vectors written in terms of the unit base vectors i and j are usually said to be written in component form.

Vectors Expressed in Terms of Two Non-Parallel Vectors

Vectors Expressed in Terms of Two Non-Parallel Vectors

Finding the magnitude of a vector The magnitude (or modulus) of a vector is given by the length of the line segment representing it. For example, suppose we have the vector A a B The magnitude of this vector is written as . We can calculate this using Pythagoras’s Theorem.

The distance between two points If we are given the coordinates of two points and we are asked to find the distance between them we use Pythagoras’ Theorem in the same way. For example, Find the distance between the points with coordinates P(-4, 7) and Q(-7, 11). If d is the distance between the points then, using Pythagoras’ Theorem in three dimensions gives: d 2 = (-4 – (-7))2 + (7 – 11)2 d 2 = 9 + 16 d 2 = 25 d=5 In general, if d is the distance between the points (x 1, y 1) and (x 2, y 2) then d 2 = (x 1 – x 2)2 + (y 1 – y 2)2

Unit Vectors Remember, if the magnitude of a vector is 1 it is called a unit vector. It is possible to find a unit vector parallel to any given vector, a, by dividing the vector by its magnitude. The unit vector parallel to the vector a is denoted by So, in general, Find a unit vector parallel to b = 4 i – j

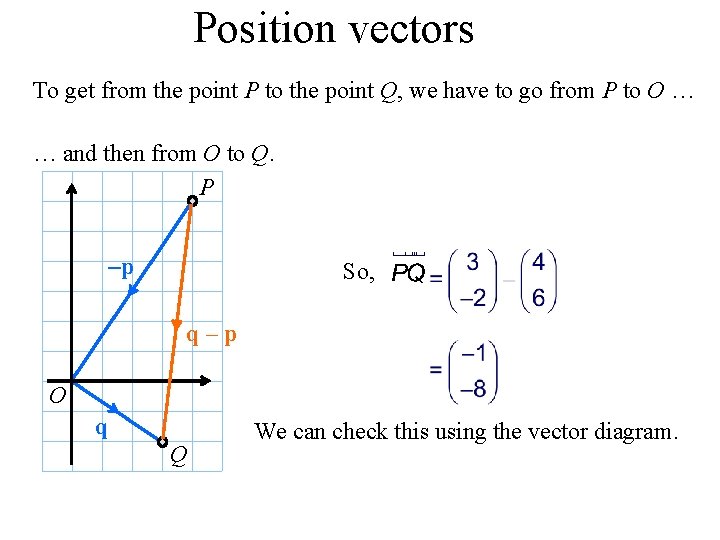
Position vectors (Page 519) A position vector is a vector that is relative to a fixed origin O. For example, suppose the point P has coordinates (4, 6). P The position vector of the point P is given by p Now, suppose the point Q has coordinates (3, – 2). The position vector of the point Q is given by O q Q Vector PQ is written as a column vector.

Position vectors To get from the point P to the point Q, we have to go from P to O … … and then from O to Q. P –p p So, q–p O q Q We can check this using the vector diagram.

Position vectors In general, if A is the point with coordinates (x 1, y 1) and B is the point with coordinate (x 2, y 2) we can write the position vectors and The vector is given by The vector can also be written in terms of i and j as

Collinear points Three or more points are said to be collinear if they lie on the same line. For example Prove that the three points A(– 3, 2), B(1, 4) and C (3, 5) are collinear. (see Page 520) Since AB is a scalar multiple of BC the two lines must be parallel. They also have the point B in common and so the points A, B and C must be collinear.