Representing Trees Paolo Ferragina Dipartimento di Informatica Universit

Representing Trees Paolo Ferragina Dipartimento di Informatica, Università di Pisa Paolo Ferragina, Università di Pisa

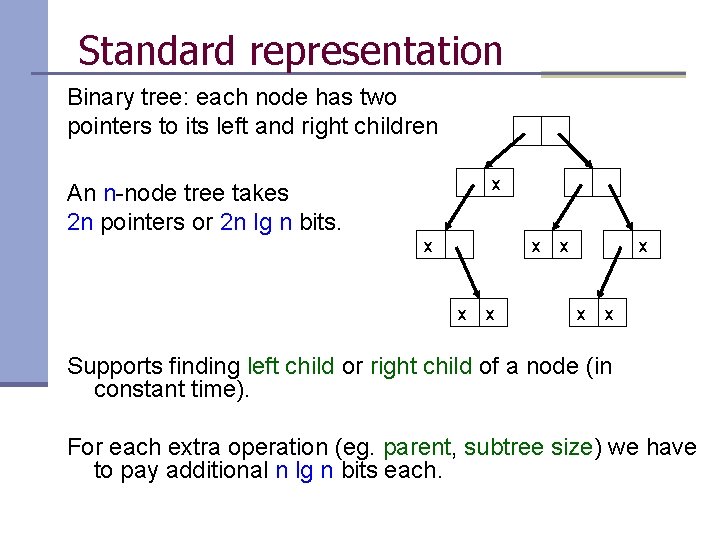
Standard representation Binary tree: each node has two pointers to its left and right children An n-node tree takes 2 n pointers or 2 n lg n bits. x x x x x Supports finding left child or right child of a node (in constant time). For each extra operation (eg. parent, subtree size) we have to pay additional n lg n bits each.

Can we improve the space bound? n There are less than 22 n distinct binary trees on n nodes. n 2 n bits are enough to distinguish between any two different binary trees. n Can we represent an n node binary tree using 2 n bits, and still be able to navigate it in constant time ?

Binary tree representation n A binary tree on n nodes can be represented using 2 n+o(n) bits to support: n n n parent left child right child in constant time.

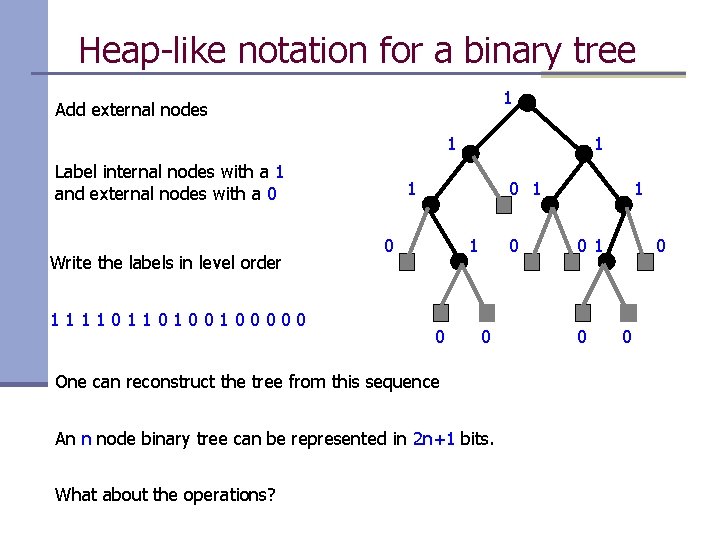
Heap-like notation for a binary tree 1 Add external nodes 1 Label internal nodes with a 1 and external nodes with a 0 Write the labels in level order 11110110100100000 1 1 0 1 0 0 0 One can reconstruct the tree from this sequence An n node binary tree can be represented in 2 n+1 bits. What about the operations? 1 01 0 0 0

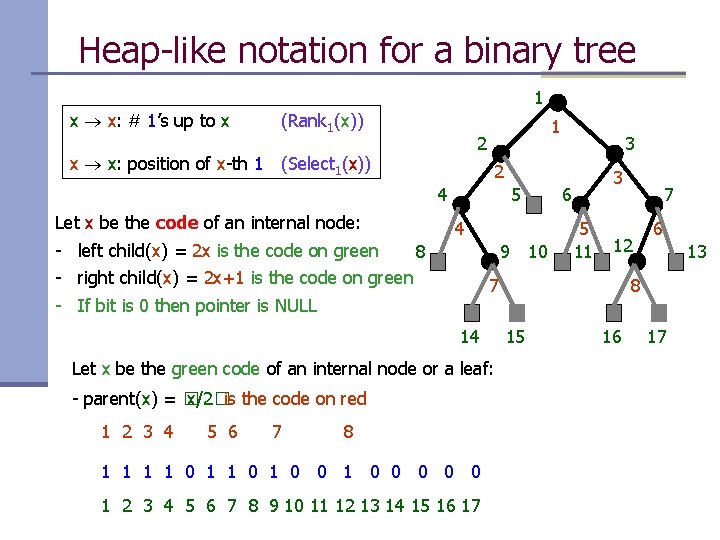
Heap-like notation for a binary tree 1 x x: # 1’s up to x (Rank 1(x)) 1 2 x x: position of x-th 1 (Select 1(x)) 2 4 Let x be the code of an internal node: - left child(x) = 2 x is the code on green 8 - right child(x) = 2 x+1 is the code on green - If bit is 0 then pointer is NULL 5 9 - parent(x) = � x/2�is the code on red 7 10 5 11 8 1 1 0 0 1 0 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 7 12 7 Let x be the green code of an internal node or a leaf: 5 6 3 6 4 14 1 2 3 4 3 6 13 8 15 16 17

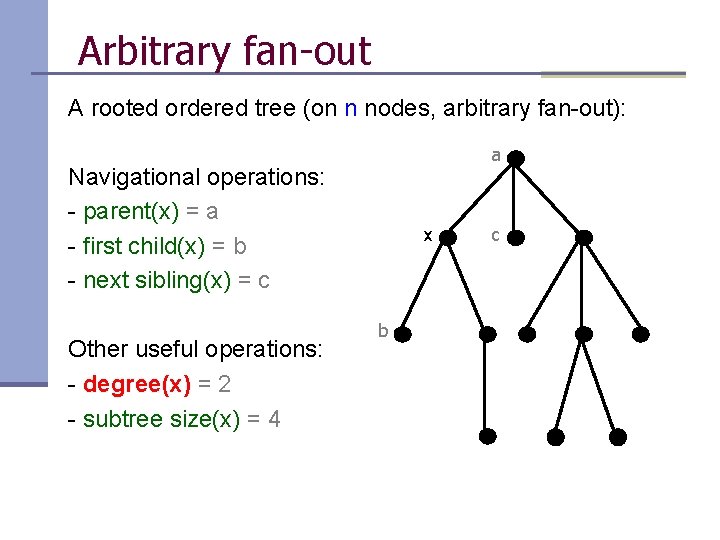
Arbitrary fan-out A rooted ordered tree (on n nodes, arbitrary fan-out): a Navigational operations: - parent(x) = a - first child(x) = b - next sibling(x) = c Other useful operations: - degree(x) = 2 - subtree size(x) = 4 x b c

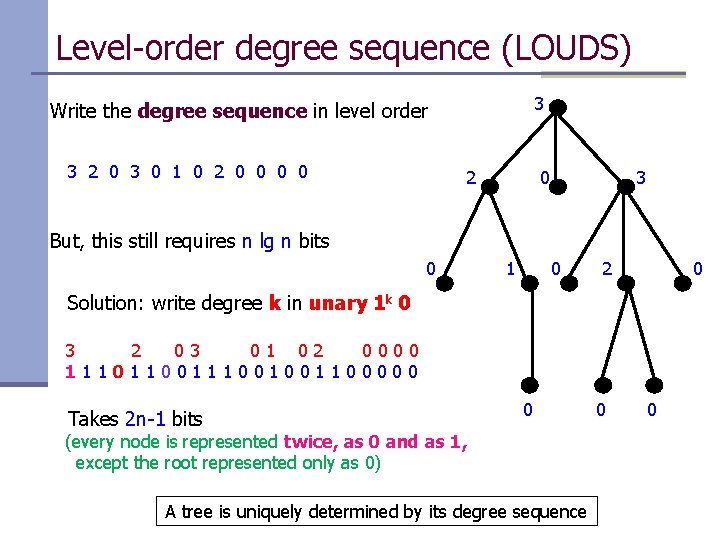
Level-order degree sequence (LOUDS) 3 Write the degree sequence in level order 3 2 0 3 0 1 0 2 0 3 But, this still requires n lg n bits 0 1 0 2 0 Solution: write degree k in unary 1 k 0 3 2 03 01 02 0000 111011001001100000 Takes 2 n-1 bits 0 (every node is represented twice, as 0 and as 1, except the root represented only as 0) A tree is uniquely determined by its degree sequence 0 0

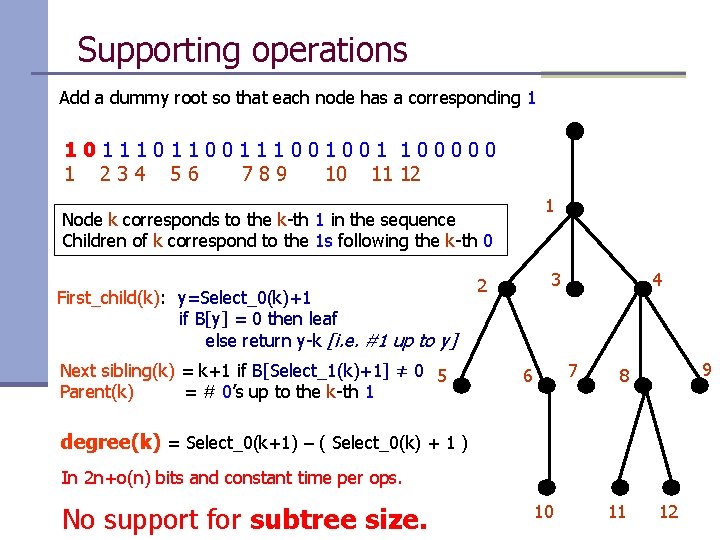
Supporting operations Add a dummy root so that each node has a corresponding 1 101100111001001 100000 1 234 56 789 10 11 12 1 Node k corresponds to the k-th 1 in the sequence Children of k correspond to the 1 s following the k-th 0 First_child(k): y=Select_0(k)+1 if B[y] = 0 then leaf else return y-k [i. e. #1 up to y] Next sibling(k) = k+1 if B[Select_1(k)+1] ≠ 0 5 Parent(k) = # 0’s up to the k-th 1 3 2 4 7 6 9 8 degree(k) = Select_0(k+1) – ( Select_0(k) + 1 ) In 2 n+o(n) bits and constant time per ops. No support for subtree size. 10 11 12