Representing Motion Chapter 2 Pop Quiz How fast

Representing Motion Chapter 2

Pop Quiz! • How fast are you moving at this moment? o A. ) 0 m/s o B. ) 783 mi/h o C. ) 350 m/s o D. ) 30 km/s

Pop Quiz! • How fast are you moving? o. A. ) 0 m/s o. B. ) 783 mi/h o. C. ) 350 m/s o. D. ) 30 km/s Speed of the earth’s rotation around its axis @ 40 o N latitude Speed of the earth’s revolution around the sun

Pop Quiz! • How fast are you moving? o. A. ) 0 m/s o. B. ) 783 mi/h o. C. ) 350 m/s o. D. ) 30 km/s Speed of the earth’s rotation around its axis @ 40 o N latitude Speed of the earth’s revolution around the sun o In order to describe motion, you need a frame of reference!

Frame of Reference • A system of objects that are not moving with respect to one another

Relative Motion • Movement in relation to a frame of reference. • Different frames of reference will give the same object different motion.

Coordinate Systems

Coordinate Systems

Coordinate Systems

Distance • The length of a path between two points • SI Unit – meter • Only length of the path is important o Direction doesn’t matter o Scalar (magnitude only)

Displacement • The strait line distance and direction between two points. • Vector (magnitude and direction)

Time Intervals •

Displacement •

Displacement If displacements are in the same direction, add the vectors. If displacements are in different directions, subtract the vectors. 3 + 3 - 2 2 =5 =1

Vector vs. Scalar Quantities • Scalar o Magnitude only • Vector o Magnitude and Direction

Scalar Quantities Vector Quantities Distance Velocity Displacement Time Temperature Force

Vectors and Motion A quantity that requires both a magnitude (or size) and a direction can be represented by a vector. Graphically, we represent a vector by an arrow. The velocity of this car is 100 m/s (magnitude) to the left (direction). This boy pushes on his friend with a force of 25 N to the right.

Displacement Vectors A displacement vector starts at an object’s initial position and ends at its final position. It doesn’t matter what the object did in between these two positions. In motion diagrams, the displacement vectors span successive particle positions. Slide 1 -29

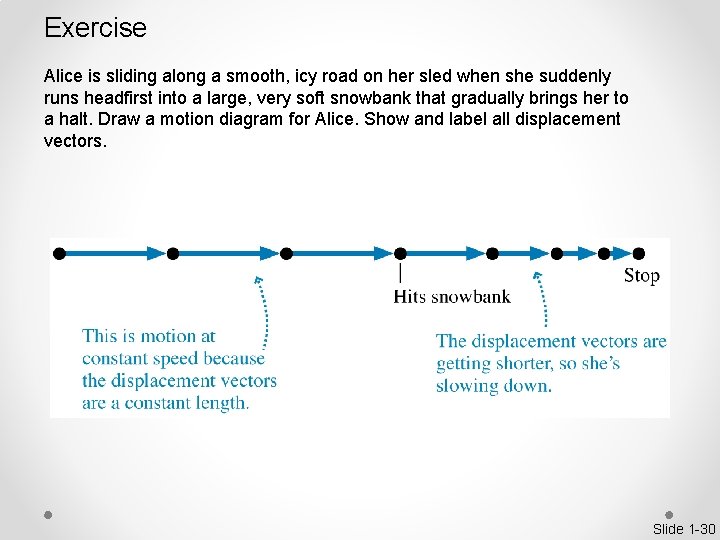
Exercise Alice is sliding along a smooth, icy road on her sled when she suddenly runs headfirst into a large, very soft snowbank that gradually brings her to a halt. Draw a motion diagram for Alice. Show and label all displacement vectors. Slide 1 -30

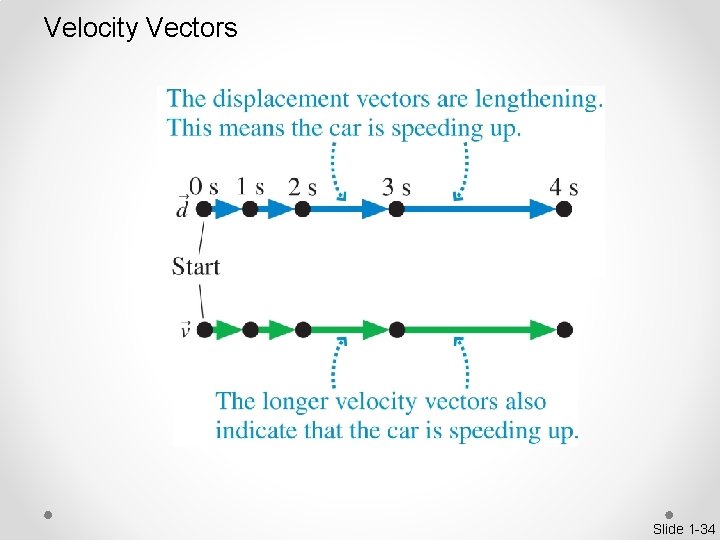
Velocity Vectors Slide 1 -34

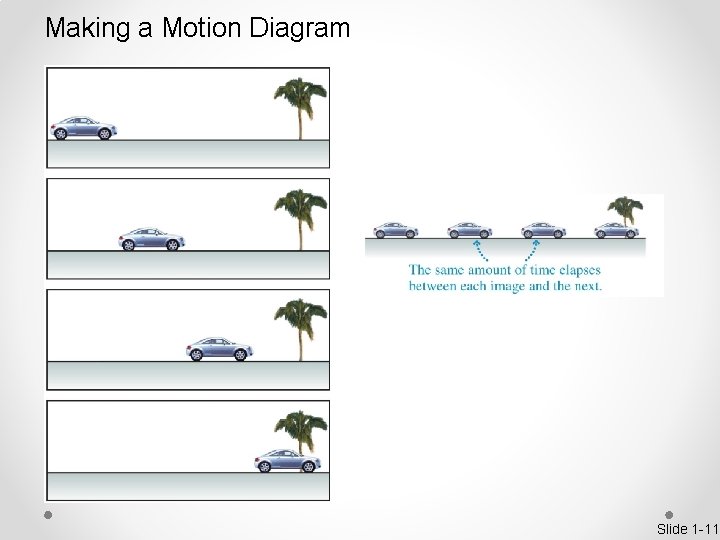
Making a Motion Diagram Slide 1 -11

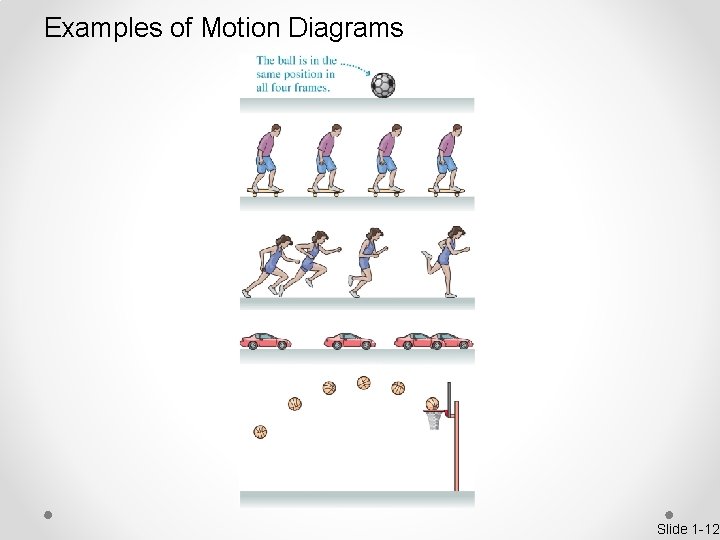
Examples of Motion Diagrams Slide 1 -12

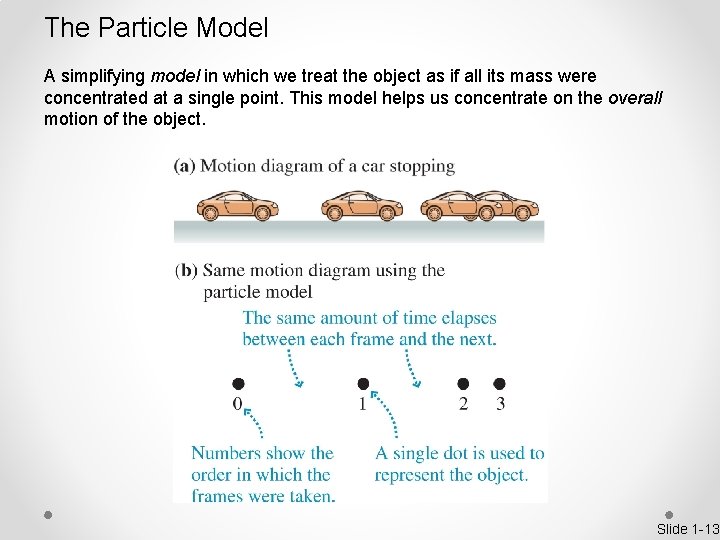
The Particle Model A simplifying model in which we treat the object as if all its mass were concentrated at a single point. This model helps us concentrate on the overall motion of the object. Slide 1 -13

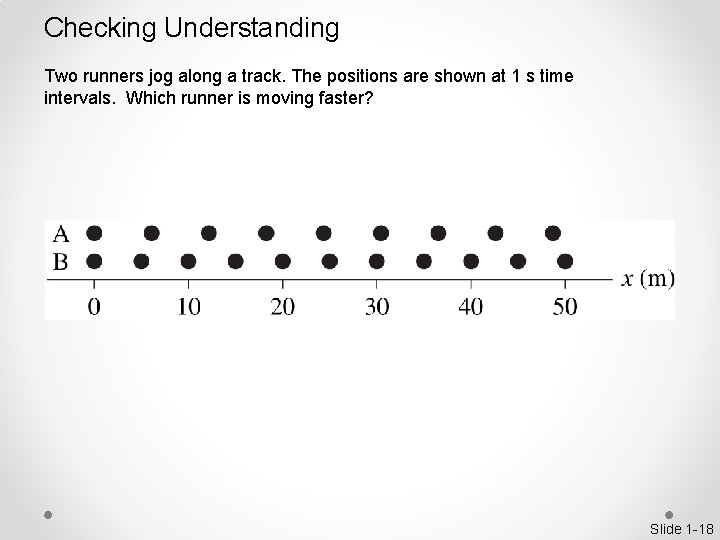
Checking Understanding Two runners jog along a track. The positions are shown at 1 s time intervals. Which runner is moving faster? Slide 1 -18

Checking Understanding Two runners jog along a track. The times at each position are shown. Which runner is moving faster? They are both moving at the same speed. Slide 1 -20

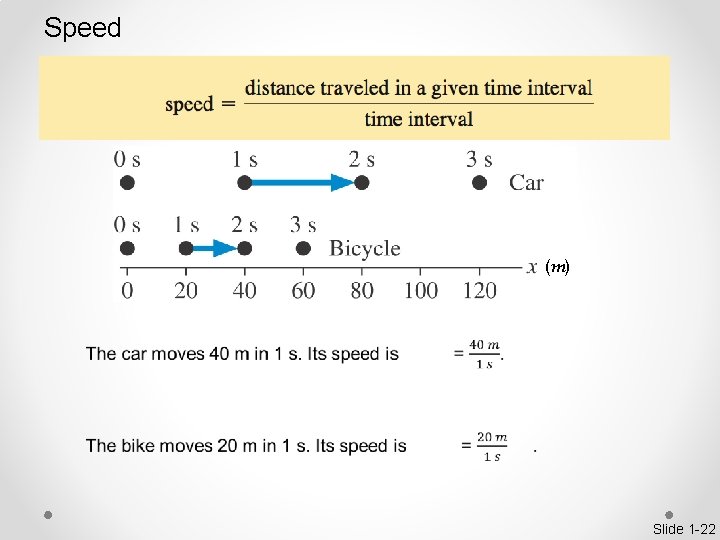
Speed (m) Slide 1 -22

Velocity Slide 1 -23

Speed and Velocity •

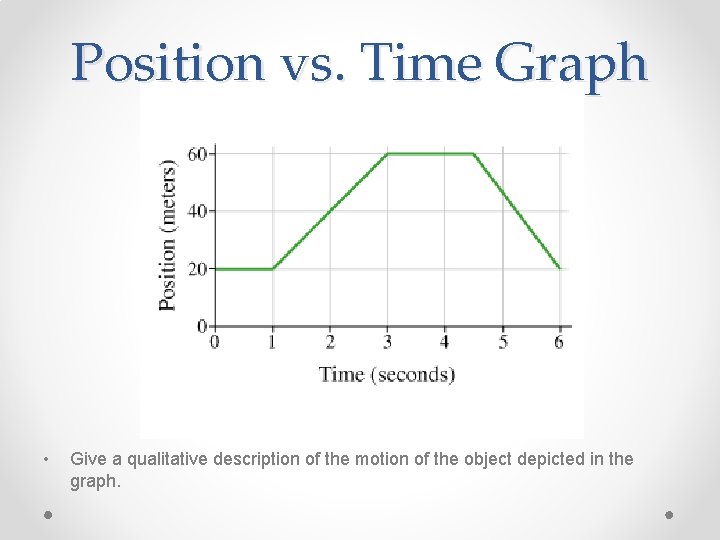
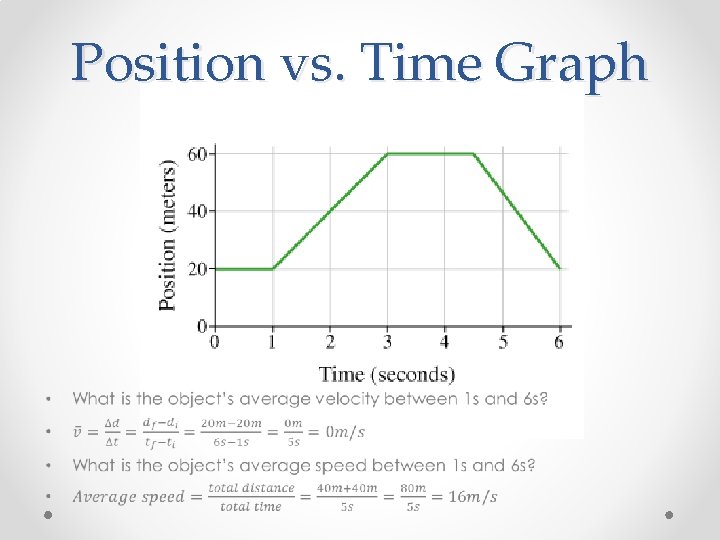
Position vs. Time Graph • Give a qualitative description of the motion of the object depicted in the graph.

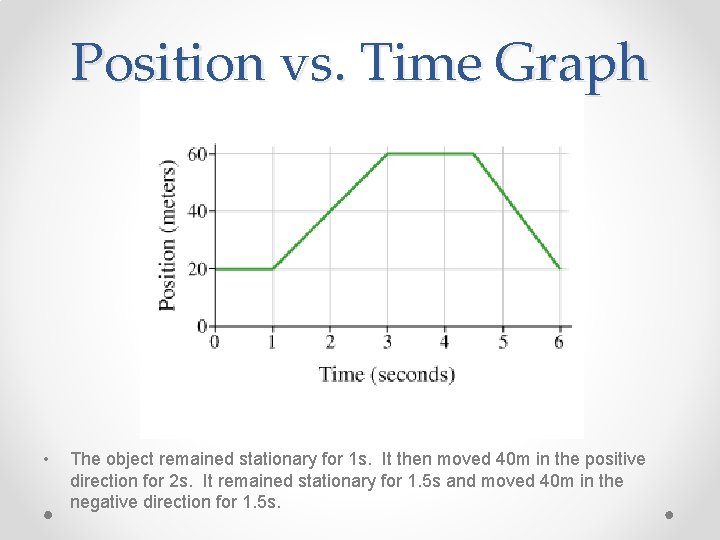
Position vs. Time Graph • The object remained stationary for 1 s. It then moved 40 m in the positive direction for 2 s. It remained stationary for 1. 5 s and moved 40 m in the negative direction for 1. 5 s.

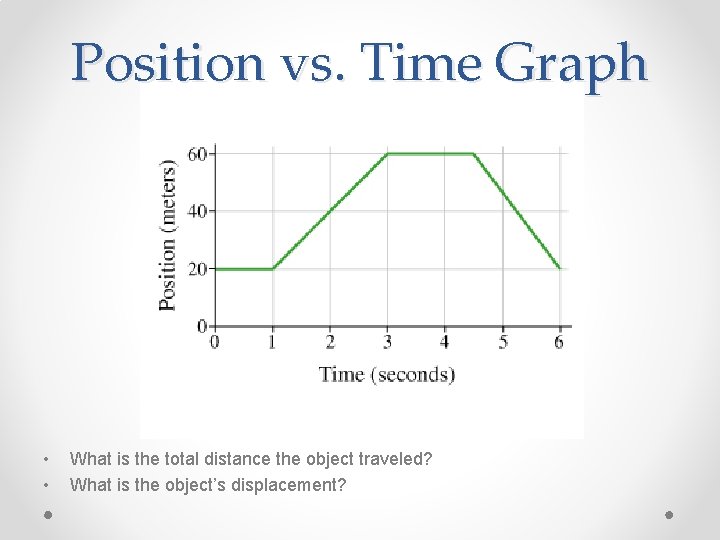
Position vs. Time Graph • • What is the total distance the object traveled? What is the object’s displacement?

Position vs. Time Graph •

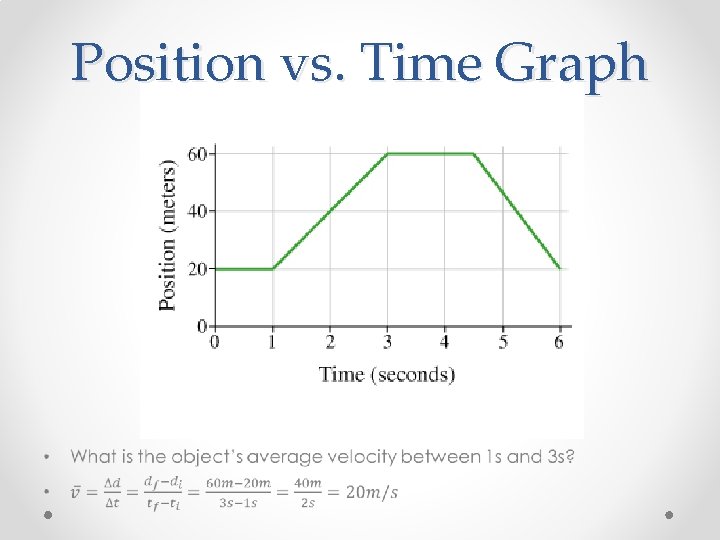
Position vs. Time Graph •

Position vs. Time Graph •

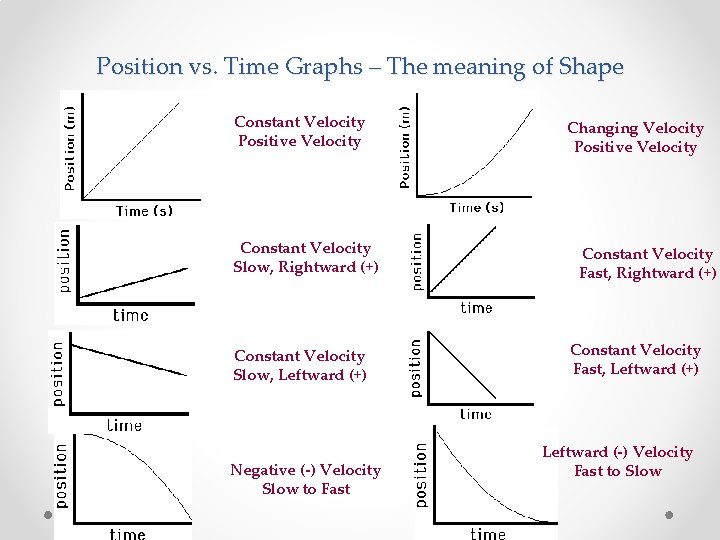
Position vs. Time Graphs – The meaning of Shape Constant Velocity Positive Velocity Constant Velocity Slow, Rightward (+) Constant Velocity Slow, Leftward (+) Negative (-) Velocity Slow to Fast Changing Velocity Positive Velocity Constant Velocity Fast, Rightward (+) Constant Velocity Fast, Leftward (+) Leftward (-) Velocity Fast to Slow

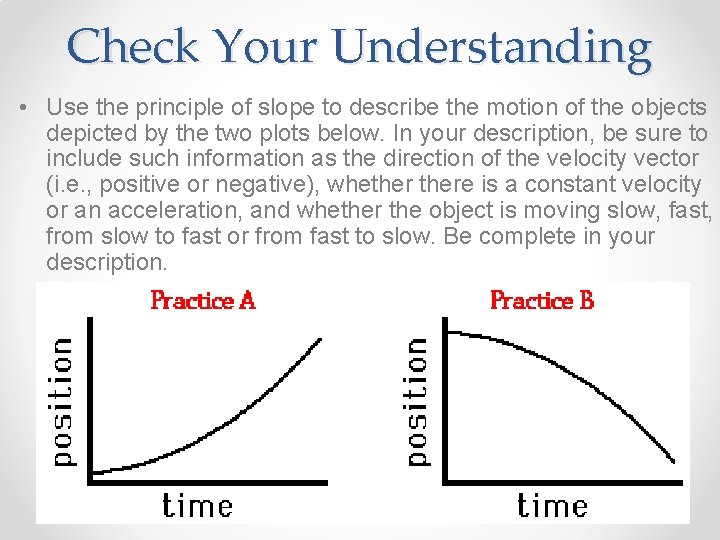
Check Your Understanding • Use the principle of slope to describe the motion of the objects depicted by the two plots below. In your description, be sure to include such information as the direction of the velocity vector (i. e. , positive or negative), whethere is a constant velocity or an acceleration, and whether the object is moving slow, fast, from slow to fast or from fast to slow. Be complete in your description.

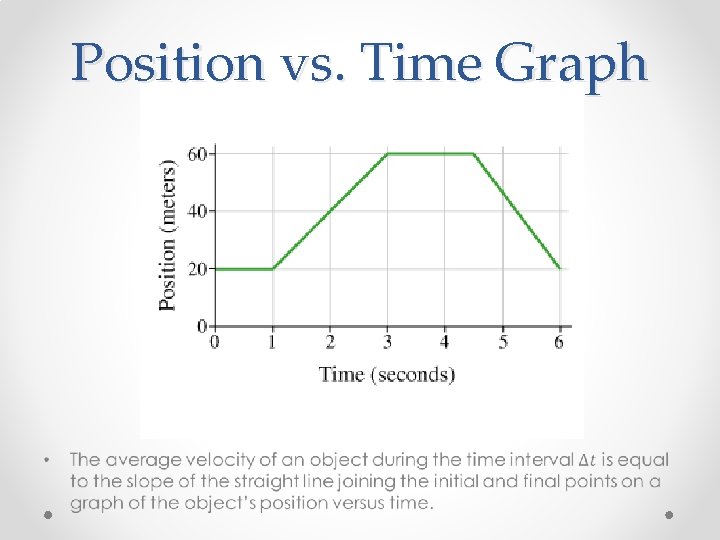
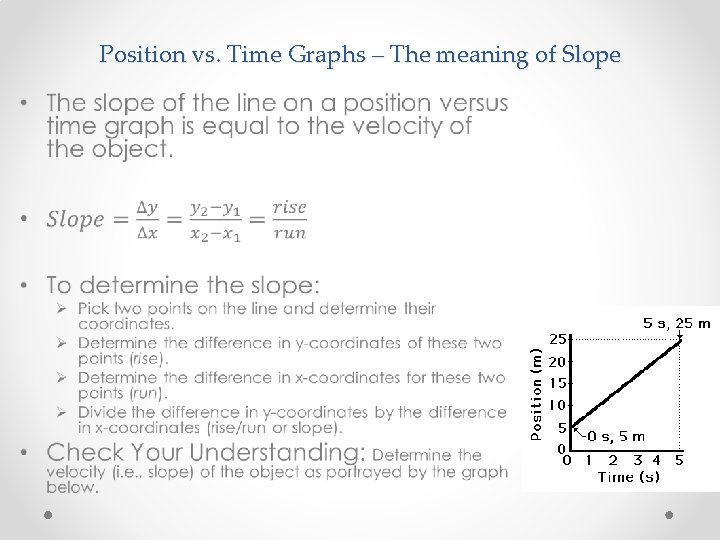
Position vs. Time Graphs – The meaning of Slope •

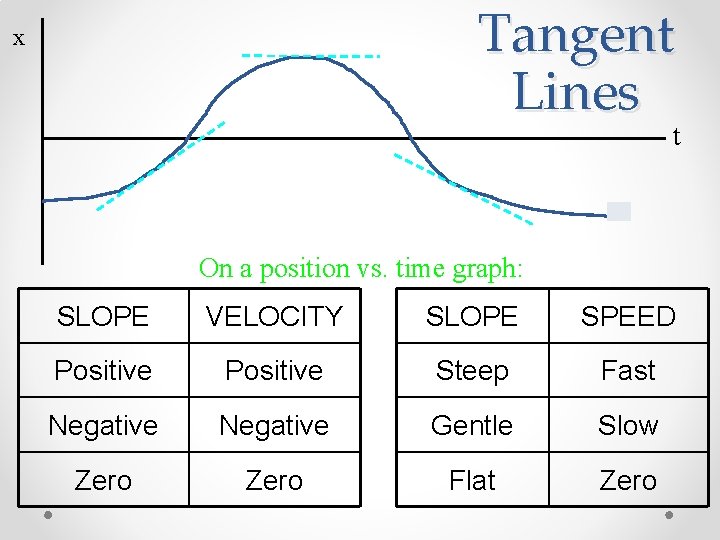
Tangent Lines x t On a position vs. time graph: SLOPE VELOCITY SLOPE SPEED Positive Steep Fast Negative Gentle Slow Zero Flat Zero

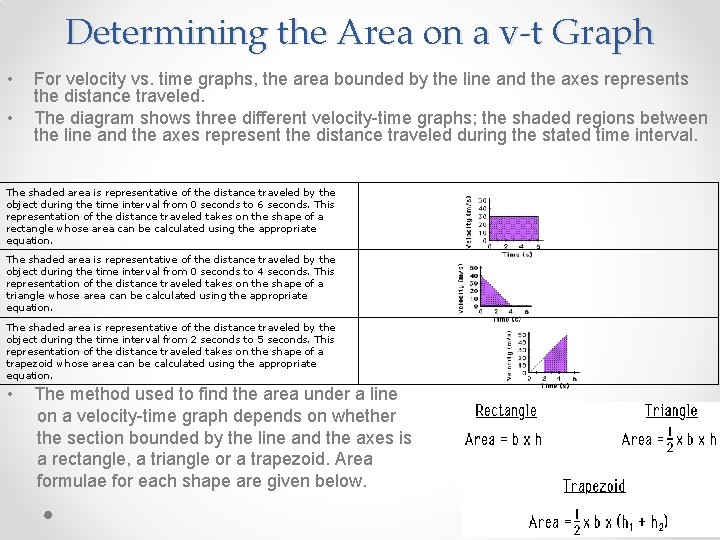
Determining the Area on a v-t Graph • • For velocity vs. time graphs, the area bounded by the line and the axes represents the distance traveled. The diagram shows three different velocity-time graphs; the shaded regions between the line and the axes represent the distance traveled during the stated time interval. The shaded area is representative of the distance traveled by the object during the time interval from 0 seconds to 6 seconds. This representation of the distance traveled takes on the shape of a rectangle whose area can be calculated using the appropriate equation. The shaded area is representative of the distance traveled by the object during the time interval from 0 seconds to 4 seconds. This representation of the distance traveled takes on the shape of a triangle whose area can be calculated using the appropriate equation. The shaded area is representative of the distance traveled by the object during the time interval from 2 seconds to 5 seconds. This representation of the distance traveled takes on the shape of a trapezoid whose area can be calculated using the appropriate equation. • The method used to find the area under a line on a velocity-time graph depends on whether the section bounded by the line and the axes is a rectangle, a triangle or a trapezoid. Area formulae for each shape are given below.

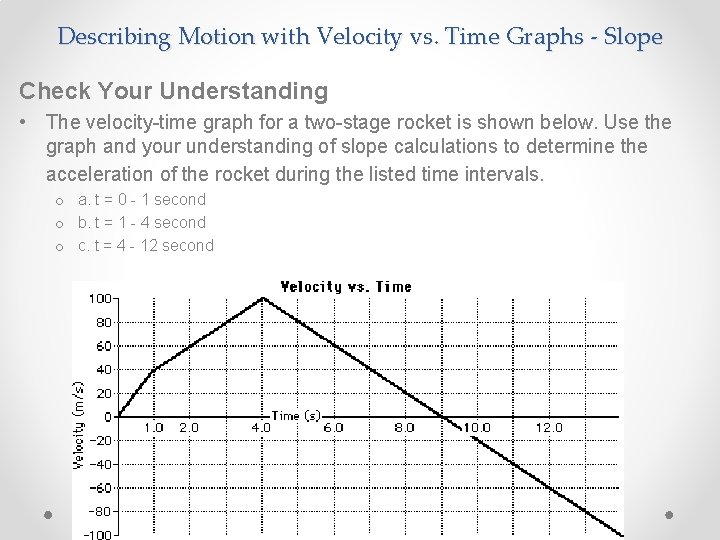
Describing Motion with Velocity vs. Time Graphs - Slope Check Your Understanding • The velocity-time graph for a two-stage rocket is shown below. Use the graph and your understanding of slope calculations to determine the acceleration of the rocket during the listed time intervals. o a. t = 0 - 1 second o b. t = 1 - 4 second o c. t = 4 - 12 second

Practice Problem • Calculate the speed of a dog running through a field if he is covering 23. 7 meters in 54 seconds.

Practice Problem • Which object has a greater velocity, a ball rolling down a 3. 4 meter hill in six seconds or a fish swimming upstream and covering 5. 4 meters in 0. 4 minutes?

Practice Problem • Calculate the velocity of a mountain climber if that climber is moving northeast at a pace of 1. 6 km in 1. 4 hours? Give your answer in the SI unit for velocity.

Practice Problem • If a cyclist in the Tour de France traveled southwest a distance of 12, 250 meters in one hour, what would the velocity of the cyclist be?

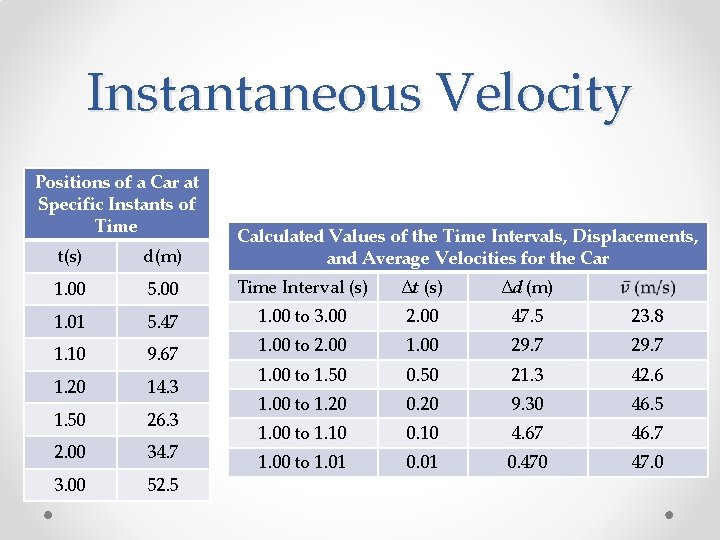
Instantaneous Velocity •

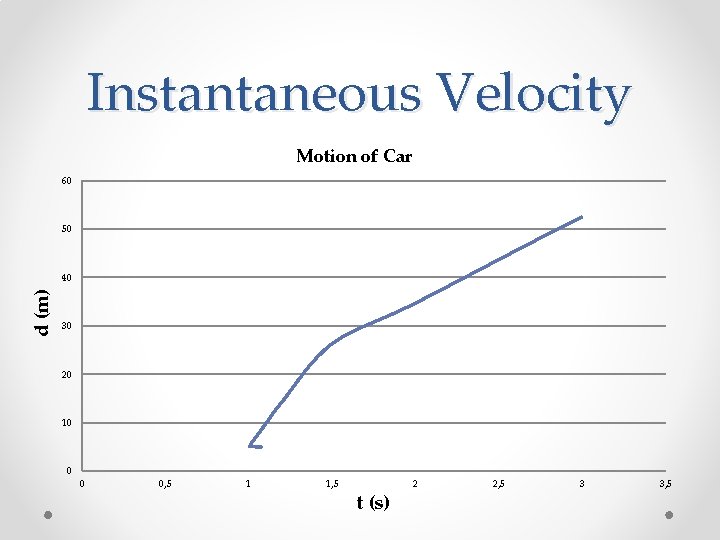
Instantaneous Velocity Positions of a Car at Specific Instants of Time t(s) d(m) Calculated Values of the Time Intervals, Displacements, and Average Velocities for the Car 1. 00 5. 00 Time Interval (s) ∆t (s) ∆d (m) 1. 01 5. 47 1. 00 to 3. 00 2. 00 47. 5 23. 8 1. 10 9. 67 1. 00 to 2. 00 1. 00 29. 7 1. 20 14. 3 1. 00 to 1. 50 0. 50 21. 3 42. 6 1. 50 26. 3 1. 00 to 1. 20 0. 20 9. 30 46. 5 2. 00 34. 7 1. 00 to 1. 10 0. 10 4. 67 46. 7 3. 00 52. 5 1. 00 to 1. 01 0. 470 47. 0

Instantaneous Velocity Motion of Car 60 50 d (m) 40 30 20 10 0 0 0, 5 1 1, 5 t (s) 2 2, 5 3 3, 5

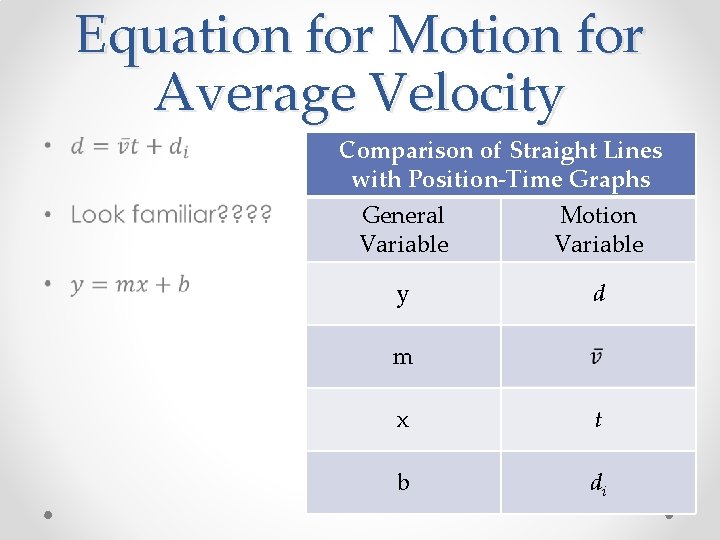
Equation for Motion for Average Velocity • Comparison of Straight Lines with Position-Time Graphs General Variable Motion Variable y d m x t b di