Representing Motion Chapter 2 2 1 Picturing Motion

Representing Motion Chapter 2

2. 1 Picturing Motion �What kinds of motion can you describe? �How do you know that an object has moved? Be specific. �Let’s start at the very beginning… Straight Line Motion.

Motion Diagrams �A series of images showing the positions of a moving object at equal time intervals is called a motion diagram. �A particle model is a simplified version of a motion diagram in which the object in motion is replaced by a series of single points.

2. 2 Where and When? Beginning Vectors �Coordinate Systems � Tells you the location of the zero point of the variable you are studying and the direction in which the values of the variable increase. � The origin is the point at which both variables have a value of zero � Position can be represented by drawing an arrow from the origin to the point representing the object’s new location �The length of the arrow indicates how far the object is from the origin or the distance.

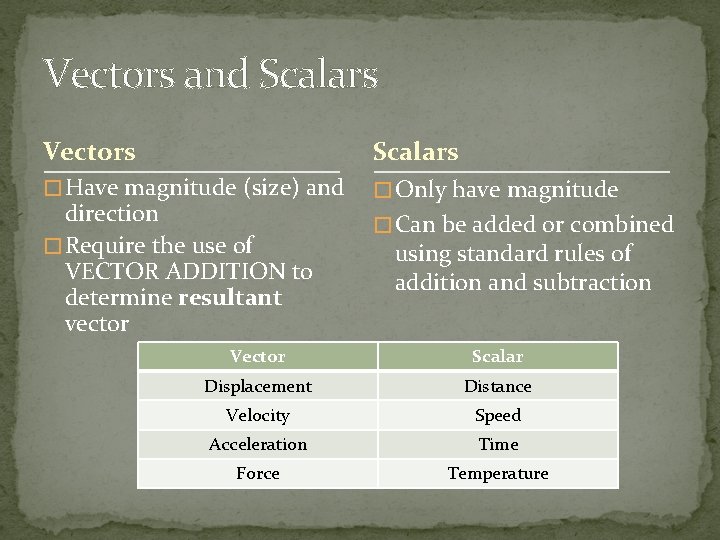
Vectors and Scalars Vectors Scalars � Have magnitude (size) and � Only have magnitude direction � Require the use of VECTOR ADDITION to determine resultant vector � Can be added or combined using standard rules of addition and subtraction Vector Scalar Displacement Distance Velocity Speed Acceleration Time Force Temperature

Vector Addition (Graphical Method) �You will need a ruler, protractor, and pencil �Draw a coordinate system (small) as your origin �Draw an arrow with the tail at the origin and the head pointing in the direction of motion. �The length of the arrow should represent the distance traveled. �Add the second vector using the head to tail method. �Measure resultant magnitude and direction.

Vector Addition (Geometry and Trig) �Add vectors using “head to tail” method. �Pictures do not need to be drawn to scale. No need for a ruler and protractor. �Use Pythagorean Theorem and SOHCAHTOA to solve for resultant vectors ONLY when RIGHT TRIANGLES are formed. �If not right triangles, use Law of Sines and Law of Cosines to solve for resultant vectors.

Time Intervals and Displacements �The difference between two times is called a time interval and is expressed as �i and f can be any two time variables you choose (according to each problem) �A change in position is referred to as displacement.

Displacement Ins and Outs �Distance ≠ Displacement �Displacement is the shortest distance from start to finish or “as the crow flies” �Draw the following: � 10 m East � -10 m � 10 m North + 12 m West

Vector Components �Every vector has x- and y- components. �In other words, a vector pointing southwest has both a south (y) and west (x) component. �Vectors can be “resolved into c 0 mponents”. �Use SOHCAHTOA to find the x- and y- components

Vector Addition (x- y- Component Method) �Break EACH vector into x- and y- components. �Assign negative and positive values to each component according to quadrant rules. For instance, south would have a negative sign. �Add the x- column. Add the y- column. �Use Pythagorean Theorem to determine the final displacement magnitude. �Use SOHCAHTOA to find the final displacement direction.

2. 3 Position – Time Graphs � Plot time on the x-axis and position on the y-axis � Slope will indicate average velocity � Use this website for extra help. http: //www. physicsclassroom. com/Class/1 DKin/U 1 L 3 a. cfm Shape of Slope Interpretation Linear Constant speed (can be positive or negative) Parabolic Speeding up Hyperbola Slowing down

2. 4 How Fast? �Average velocity is defined as the change in position, divided by the time during which the change occurred. �On a position vs. time graph, both magnitude and relative direction of displacement are given. A negative slope indicates an object moving toward the zero position. Speed simply indicates magnitude or “how fast. ” Velocity indicates BOTH magnitude and direction. In other words velocity tells you “how fast” and “where. ”

Instantaneous Velocity �When solving for average velocity, two points for position and time are chosen for comparison. Individual changes in speed could have taken place within those intervals. �Instantaneous velocity represents the speed and direction of an object at a particular instant. �On a position-time graph, instantaneous velocity can be found by determining the slope of a tangent line on the curve at an given instant.

Expressing Motion in Terms of An Equation �So far, we have looked at motion diagrams, particle models, and graphs as a means of representing motion. �Equations are also quite useful. �Based on the equation y=mx +b, one final equation will be derived in this chapter. d = final position v = average velocity t = time interval di = initial position (based on y-intercept if using a graph)

Final Thoughts �Read Chapter 1! You will reinforce all of these concepts, drill them into your head and see more examples than I have given here. �Visit www. physicsclassroom. com This website offers great explanations of physics concepts. �Watch this video. It is a little boring but very helpful. http: //www. youtube. com/watch? v=4 J-m. Uek-z. Gw