REPRESENTING LINEAR INEQUALITIES ON GRAPHS You can represent
- Slides: 8
REPRESENTING LINEAR INEQUALITIES ON GRAPHS
You can represent an inequality on a graph. There are some important rules to follow. • If the inequality is ≥ or ≤ the boundary line for the region is shown by a solid line. • If the inequality is > or < the boundary line for the region is shown as a broken (dashed) line. • You are expected to shade the unwanted region. (This will leave the required region clear. )
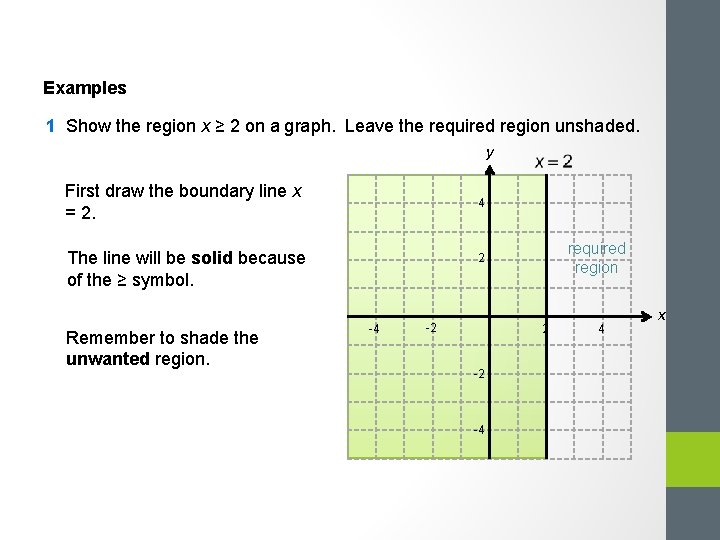
Examples 1 Show the region x ≥ 2 on a graph. Leave the required region unshaded. y First draw the boundary line x = 2. 4 The line will be solid because of the ≥ symbol. Remember to shade the unwanted region. required region 2 -4 -2 2 -2 -4 4 x
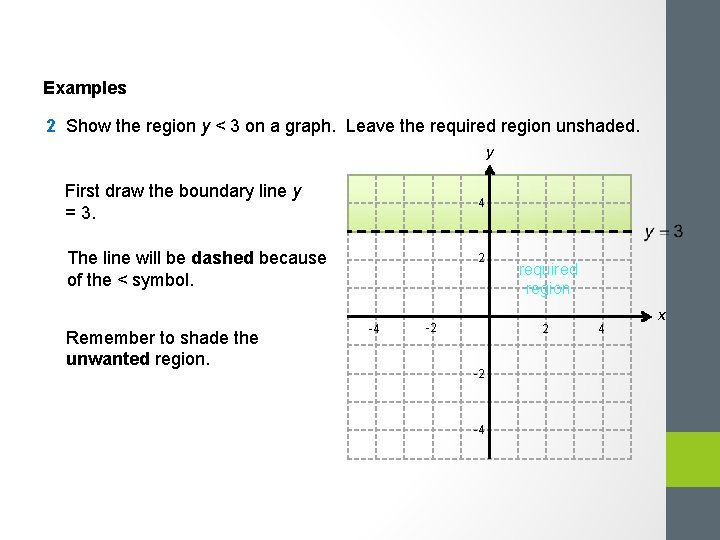
Examples 2 Show the region y < 3 on a graph. Leave the required region unshaded. y First draw the boundary line y = 3. 4 The line will be dashed because of the < symbol. Remember to shade the unwanted region. 2 -4 -2 required region 2 -2 -4 4 x
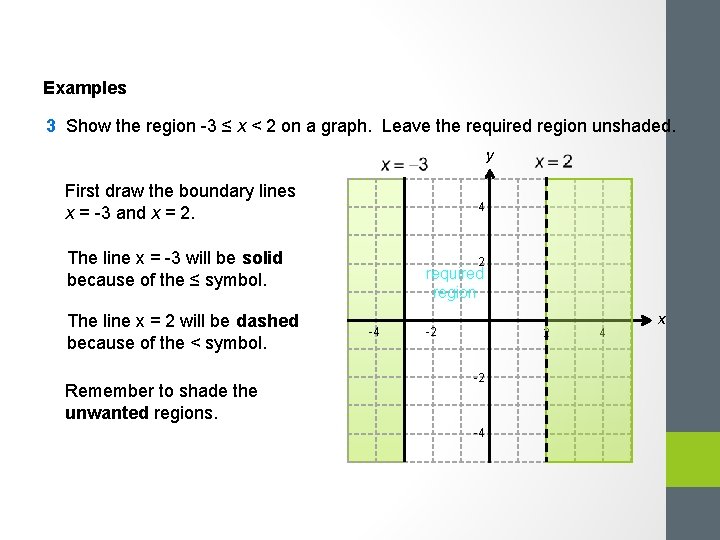
Examples 3 Show the region -3 ≤ x < 2 on a graph. Leave the required region unshaded. y First draw the boundary lines x = -3 and x = 2. 4 The line x = -3 will be solid because of the ≤ symbol. The line x = 2 will be dashed because of the < symbol. Remember to shade the unwanted regions. 2 required region -4 -2 2 -2 -4 4 x
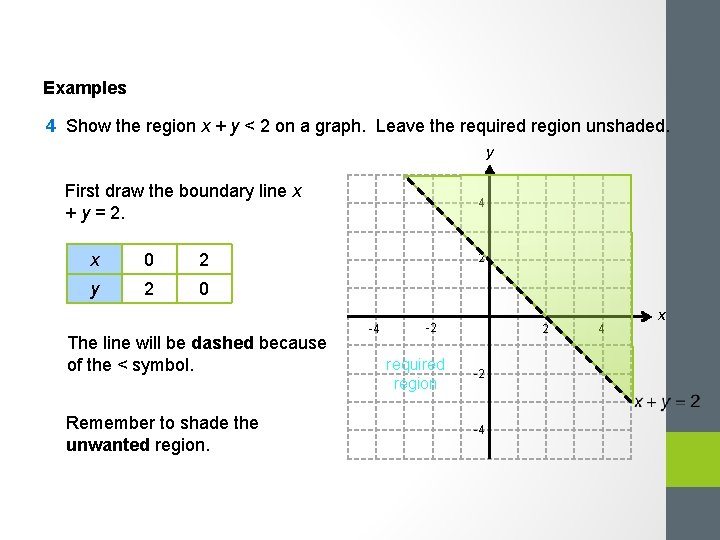
Examples 4 Show the region x + y < 2 on a graph. Leave the required region unshaded. y First draw the boundary line x + y = 2. x 0 2 y 2 0 The line will be dashed because of the < symbol. Remember to shade the unwanted region. 4 2 -4 -2 required region 2 -2 -4 4 x
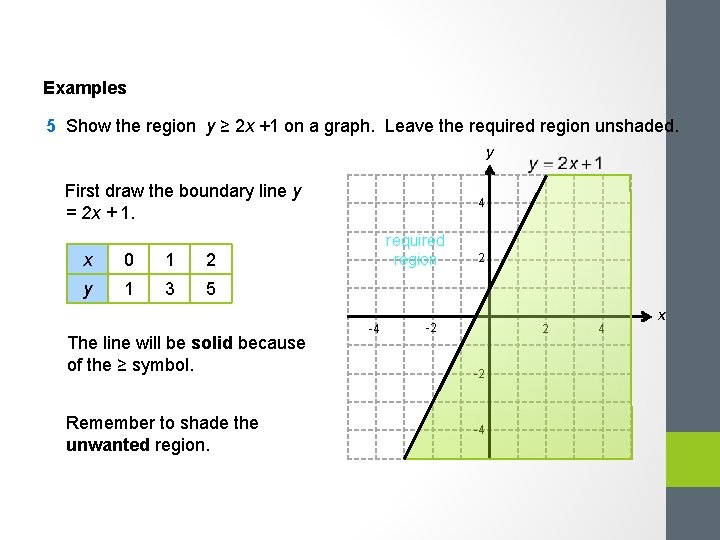
Examples 5 Show the region y ≥ 2 x +1 on a graph. Leave the required region unshaded. y First draw the boundary line y = 2 x + 1. x 0 1 2 y 1 3 5 The line will be solid because of the ≥ symbol. Remember to shade the unwanted region. 4 required region -4 2 -2 -4 4 x
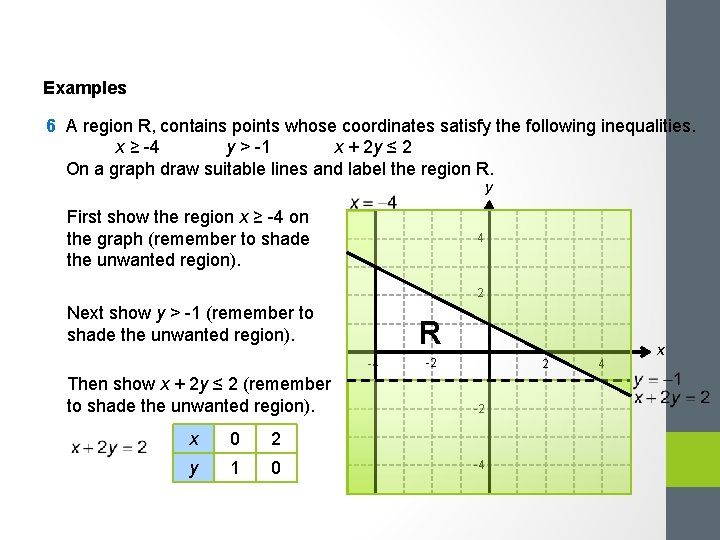
Examples 6 A region R, contains points whose coordinates satisfy the following inequalities. x ≥ -4 y > -1 x + 2 y ≤ 2 On a graph draw suitable lines and label the region R. y First show the region x ≥ -4 on the graph (remember to shade the unwanted region). 4 2 Next show y > -1 (remember to shade the unwanted region). R -4 Then show x + 2 y ≤ 2 (remember to shade the unwanted region). x 0 2 y 1 0 -2 2 -2 -4 4 x
Represent linear inequalities
If you think you can you can poem
Representing graphs and graph isomorphism
Representing graphs and graph isomorphism
How to solve an inequality graphically
Graphs that represent a function
Jenis graph
If you can imagine it you can achieve it
If you cant measure it you can't manage it
