Representation of Numbers and Arithmetic and Logical Operation

Representation of Numbers and Arithmetic and Logical Operation on them Sahar Mosleh California State University San Marcos Page 1

Representation of Numbers • In general, a number expressed in base r is written as (…. . a 3, a 2, a 1, a 0)r • Where the ai are the symbols of the number system. • The base r tells us how many different symbols the ai can have • For example: • r = 10 • r=2 • r=8 • r = 16 Sahar Mosleh ai ai e {0, 1, 2, 3, 4, 5, 6 7, 8, 9} e {0, 1, 2, 3, 4, 5, 6 7} e {0, 1, 2, 3, 4, 5, 6 7, 8, 9, A, B, C, D, E, F} California State University San Marcos Page 2

• The right most symbol of a 0 is called the least significant digit (LSD) While the left most symbol of an-1 is called most significant digit (MSD) MSD LSD • Example: 1000110010 Sahar Mosleh California State University San Marcos Page 3

Value of Numbers • In digital systems, the determination of value of signed numbers (positive and negative numbers) is different than unsigned numbers (just positive numbers) Value of Unsigned Numbers: • The value of unsigned number • Value {(…. a 3 a 2 a 1 a 0)r} = …. + a 3 r 3 + a 2 r 2+a 1 r 1+a 0 r 0 • In which ai is the ith coefficient and • r is the base • Example: • (15)10 = 1*101 + 5*100 = 10 + 5 • (1010)2 = 1*23 + 0*22 + 1*21 + 0*20 = 8+2=(10)10 • (B 7)16 = B*161 + 7*160 = 11*16 + 7 = (183)10 Sahar Mosleh California State University San Marcos Page 4

Binary to Decimal Conversion (Unsigned Numbers) Example: (0001 1001)2 = (…. b 2 b 1 b 0)10 ? 0001 1001 = 1*24 + 1* 23 + 0*22 + 0*21 + 1*20 = (25)10 Example: (1101 0111 )2 = (…. b 2 b 1 b 0)10 ? 1101 0111 = 1*27 + 1* 26 + 0*25 + 1*24 + 0*23 + 1* 22 + 1*21 + 1*20 = (215)10 Sahar Mosleh California State University San Marcos Page 5

Decimal To Binary Conversion (Unsigned Numbers) • To convert from base 10 (decimal to binary) we need to divide the number in base 10 which is (N)10 by 2 several times until division by 2 is no longer possible. (dividend becomes 0) • Example: • (121) 10 = ( … b 3 b 2 b 1 b 0)2 • (121) 10 = (1111001)2 Number Dividend Remainder 121 / 2 60 1 60 /2 30 0 30 /2 15 0 7 1 3 1 1 1 0 1 15 /2 1) Given the number in base 10 7 /2 (a 3 a 2 a 1 a 0)10 3 /2 2) Divide the number by 2 several times until dividend becomes 0 1 / 2 3) write the remainders from bottom to top 4) This is the representation of (N)10 in (N)2 Sahar Mosleh California State University San Marcos Page 6

Hex To Binary Conversion (Unsigned Numbers) • A Hex representation of any number can be converted to its binary representation directly by determining the 4 bit binary representation of each hex digit and concatenating the 4 bit binary word in which the hex digit appears • For (ABC)16 = (…. b 3 b 2 b 1 b 0)2 (A)16 = (1010) 2 (B)16 = (1011) 2 (C) 16 = (1100) 2 • Therefore, (ABC)16 = (1010 1011 1100)2 Sahar Mosleh California State University San Marcos Page 7

• The binary representation of any number can be converted to the hex representation by partitioning the binary number into groups of 4 digits starting from LSD (the rightmost digit) to left • Example: (01 1011)2 = (…. . b 3 b 2 b 1 b 0)16 (1 B)16 • Example: • (1 1011 1101 1111 0001 1111 0101)2 = (…. . b 3 b 2 b 1 b 0)16 1 BDF 1 F 5 Sahar Mosleh = (1 BDF 1 F 5) 16 California State University San Marcos Page 8

Reasons for Using Hex Numbers • Computer and digital systems operate on binary numbers. • Binary numbers {0, 1} constitute the building blocks of computer machine language • Hex representation of a binary number is easier and more convenient for humans to communicate • Converting between hex and binary representation of the number is easy Sahar Mosleh California State University San Marcos Page 9

Bitwise Addition of Binary Numbers (Unsigned Numbers) • Example: • Add binary number A = 11101100 B = 01110011 and • Do the addition one column at a time A B Result Sahar Mosleh 1 1 11101100 + 01110011 -------101011111 California State University San Marcos Page 10

Signed Numbers and Signed Arithmetic • There are only two symbols in the binary number system, digital systems do not know of the existence of negative and positive numbers. • They only know magnitude or positive binary numbers • In digital world, there are no symbol for ‘+’ or ‘-’ • However, we require positive and negative binary numbers to be processed by the computer. • When using the signed number system, we will interpret the string of binary bits differently Sahar Mosleh California State University San Marcos Page 11

• Let us construct a system containing one half positive and other half negative numbers • Let the MSB (most significant bit) denote the sign of the binary number where if the • MSB = 0 positive number • MSB = 1 negative number MSB & Sign bit LSB 01111111 • Note that the sign bit does not contribute to the magnitude Sahar Mosleh California State University San Marcos Page 12

8 -bit Representation of Signed Binary Number 0000. . . 0111 0000 0001 0010 0 1000. . . 1111 0000 -128 0001 0010 1101 1110 1111 127 1101 1110 1111 -1 Sahar Mosleh • Range of positive numbers: • 0 through 2(8 -1) -1 = 127 • In general, for n-bit binary words 0 through 2(n-1) -1 • Range of the negative numbers: • -1 through -2(8 -1) = -128 • In general, for n-bit binary words -1 through -2(n-1) California State University San Marcos Page 13
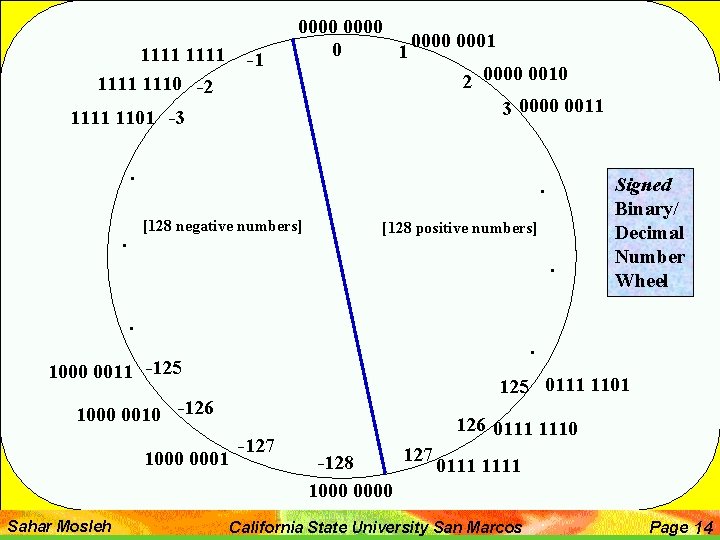
1111 1110 -2 -1 0000 0001 0 1 2 0000 0010 3 0000 0011 1101 -3. . [128 negative numbers] . [128 positive numbers] . Signed Binary/ Decimal Number Wheel . . 1000 0011 -125 0111 1101 1000 0010 -126 1000 0001 Sahar Mosleh -127 126 0111 1110 127 -128 0111 1000 0000 California State University San Marcos Page 14

2’s Complement Representation of Signed Numbers • We now have two methods for representing and interpreting strings of binary numbers 1) When it is sufficient to consider only positive numbers, we use the unsigned interpretation as discussed earlier 2) When we want to consider both positive and negative numbers, we use the signed number wheel • The interpretation of the numbers in the signed number wheel is called the 2’s complement representation. • This wheel shows us the binary equivalent of signed decimal numbers, or, the decimal equivalent of signed binary numbers. Sahar Mosleh California State University San Marcos Page 15

How to Obtain the Signed Binary Number from a Signed Small Decimal Number ? • If the signed decimal number is positive, • Convert the decimal number to binary using the unsigned conversion process as discussed earlier • If the signed decimal number is negative, then 1) Determine the binary number representation of the absolute value of signed decimal number 2) Take the 1’s complement of the number (flipping every single bit: 0 to 1 and 1 to 0) 3) Add 1 to it Sahar Mosleh California State University San Marcos Page 16

Converting a Positive Decimal Number to the 2’s Complement Representation: • Example: Represent (+18)10 as a signed 8 -bit binary number • Using unsigned number conversion process Number Dividend Remainder 18 / 2 9 0 9 /2 4 1 4 /2 2 0 2 /2 1 0 1/2 0 1 Sahar Mosleh The signed conversion is: (+18)10 = (00010010 )2 California State University San Marcos Page 17

Converting a Negative Decimal Number to the 2’s Complement Representation: • Represent (-18)10 as a signed 8 -bit binary number • Solution: • Abs(-18)10 : 0001 0010 1 • 1’s Complement: • Add 1: • Result: 1110 1101 + 0000 0001 1110 • Therefore, (-18)10 = (1110) 2 Sahar Mosleh California State University San Marcos Page 18

How to Obtain the Signed Decimal Number of a Signed Binary Number • If the signed binary number is positive (i. e. MSB = 0), convert the binary number to decimal using the unsigned conversion process as discussed earlier • If the signed binary number is negative (i. e. , MSB = 1) 1) Take the 1’s complement 2) Add 1 3) Convert to decimal using unsigned process 4) Put a negative sign in front of the decimal number Sahar Mosleh California State University San Marcos Page 19

Converting a Positive 2’s Complement Binary Number to Decimal Representation: • Example: Represent (0001 1000)2 as a signed decimal number • Since MSB = 0 then we can use unsigned conversion (0001 1000)2 = 1*24 + 1*23 + 0*22 + 0*21 + 0*20 = (24)10 Sahar Mosleh California State University San Marcos Page 20

Converting a Negative 2’s Complement Number to Decimal Representation: • Example: Represent (1001 1000)2 as a signed decimal number • Since MSB = 1 then the number is negative • Use signed conversion process • Solution: The number: 1001 1000 1’s Complement: 0110 0111 Add 1: + 0000 0001 Result: Decimal -ve sign • Therefore Sahar Mosleh 0110 1000 104 -104 (1001 1000)2 = (-104)10 California State University San Marcos Page 21

Signed or 2’s Complement Arithmetic Addition of 8 -bit signed number : • If both numbers are positive, use unsigned addition process. (perform bitwise addition) • Note: If the result of the addition exceed 8 -bits, then ignore the carry over bit. This is because the sum or difference of any two properly represented 8 -bits signed number never exceeds 8 -bits Addition of 8 -bit positive signed number Example: perform the addition of (8)10 + (10)10 in binary 1 + 0000 1000 0000 1010 0001 0010 (0001 0010)2 = 1*24 + 0*23 + 0*22 + 1*21 + 0*20 = (18)10 Sahar Mosleh California State University San Marcos Page 22

Addition of 8 -bit (positive and negative) signed number: • Perform the addition: 8 + (-17) • Find the 2’s complement representation (8)10 (-17)10 = = 0000 1000 ? ? ? (17)2 0001 1’s complement: 1110 Add 1 + 0000 0001 Result 1110 1111 • Therefore (-17)10 = (1110 1111)2 Sahar Mosleh California State University San Marcos Page 23

• Now (8)10 (-17)10 Result 0000 1000 + 1110 1111 (1111 0111)2 = (? ) 10 • Convert the result to decimal representation: 1111 0111 take 1’s complement 0000 1000 Add 1 + 0000 0001 Result (0000 1001)2 = (+9)10 Therefore, (1111 0111)2 is -9 in decimal Sahar Mosleh California State University San Marcos Page 24

• Example: Perform 65 – 68 in 8 bits signed numbering system. • 65 – 68 is the same as (65)10 + (-68)10. • The example is the same as the previous one. Therefore, you can follow the same step as explained to solve this problem • Example: Perform -26 – 35 in 8 bits signed numbering system. • -26 – 35 is the same as (-26)10 + (-35)10 • The example is the same as the previous one. Therefore, you can follow the same step as explained to solve this problem Sahar Mosleh California State University San Marcos Page 25

Logical Operation • The logical operators And, Or, Xor, Not are used to perform logical operation on 2 bits. The next few slides shows the performance of logical operators on all possible combination of two bits. • To perform, any logical operation on two 8 -bits binary numbers: • Write two binary numbers and perform bit-wise logical operation on each bit of the two binary numbers. Sahar Mosleh California State University San Marcos Page 26

Logical OR: • A or B Number Binary 8 -bit A B 1110 1100 0111 0011 Result 1111 A B A or B 1 1 0 0 0 A B A and B 1 1 0 0 0 1 0 0 Logical And: • A and B Number A B Result Sahar Mosleh Binary 8 -bit 1110 1100 0111 0011 0110 0000 California State University San Marcos Page 27

Logical XOR: • A xor B 1 1 0 Number Binary 8 -bit A B 1110 1100 0111 0011 1 0 1 1 Result 1001 1111 0 0 0 Logical NOT: • Not A Sahar Mosleh Number Binary 8 -bit A Not A A 1110 1100 1 0 Result 0001 0011 0 1 California State University San Marcos Page 28
- Slides: 28